抛锚撞击水下管汇的数值模拟研究

娄 敏，王艳红，明海芹

(1. 中国石油大学(华东) 石油工程学院，山东 青岛 266580；2.中集来福士海洋工程有限公司，山东 烟台 264000)

抛锚撞击水下管汇的数值模拟研究

娄 敏1，王艳红1，明海芹2

(1. 中国石油大学(华东) 石油工程学院，山东 青岛 266580；2.中集来福士海洋工程有限公司，山东 烟台 264000)

船舶抛锚撞击水下管汇会影响到管汇的正常作业，基于ANSYS/LS-DYNA动力学分析软件，建立锚-水下管汇-海床土体的三维有限元模型，对抛锚碰撞水下管汇的过程进行数值仿真。通过求解水下管汇受碰撞后的等效应力、应变的时间历程及受撞击部位的凹陷损伤深度，发现最大等效应力点出现在管汇与锚接触位置处，管汇的碰撞部位最终发生凹痕变形。同时讨论锚与管汇接触面的形状以及海床土体对水下管汇损伤程度的影响，当冲击能量相同时，锚与水下管汇的碰撞接触面积越小，水下管汇的损伤深度就越大；当锚与管汇接触的接触面积相同时，冲击能量越大，水下管汇的损伤变形越大。海床土体的剪切弹性模量对管汇的凹陷损伤深度以及最大等效应力影响与冲击能量有关，海床土体的内摩擦角对管汇的碰撞影响较小。

水下管汇；碰撞损伤；数值仿真；船舶抛锚；海床土体；水下生产系统

Abstract: The impact of the ship's anchor on the submarine manifold will affect the normal operation of a manifold. Based on ANSYS/LS-DYNA—the dynamics analysis software, and by establishing a 3D finite element model of anchor, submarine manifold and seabed soil, the process of a submarine manifold impacted by anchor is simulated. By computing the time history of equivalent stress and strain and the dent depths of the impacted elements of submarine manifold, it is found that the maximum equivalent stress appears in the contact position between the manifold and the anchor, eventually the collision part of manifold will have dent deformation. At the same time, the effect of the interface’s shape between anchor and manifold, and the seabed soil are discussed. When the impact energy is identical, the smaller the contact area between anchor and submarine manifold, the greater the damage depth of the submarine manifold; when the contact area between anchor and submarine manifold is definite, the greater the impact energy, the larger the damage deformation the submarine manifold will suffer.The effect of the shear modulus of seabed soil on the depression damage depth of a manifold and the maximum equivalent stress is related to the impact energy, and the internal friction angle of the seabed soil has little effect on the impact of the manifold.

Keywords: submarine manifold; collision damage; numerical simulation; anchor; seabed soil; submarine production system

水下生产系统由于其在开发深水油气田和边际油气田时具有明显的综合经济优势，已被世界上很多国家作为油田开发的一种重要方式广泛研究和应用[1]。近年来水下生产系统在国内的应用逐步增多，水下管汇作为水下生产系统中的一个重要组成部分，是一种基于重力的大型水下设备，作为油、气生产的汇集和分配中心，主要将不同井口产出的多路流体汇集后，借助尽可能少的管线外输，同时向各个井口分配流体，进行注水、注气、注化学药剂等操作，能够极大地优化海底生产设施的布局，减少管线的使用数量。由于水下管汇生产作业条件的特殊性，一旦发生失效，不但会对生产活动与生活造成影响，造成巨大的经济损失，还会造成海洋环境的污染，甚至引发生态灾难。因此，对水下管汇进行分析研究是很有必要的。

目前国外水下生产技术已较为成熟，有一定的应用基础。我国水下生产系统的设计、建造和安装尚处于起步阶段，工程经验缺乏，技术储备较少，同国外相比差距很大，这一现状影响了我国深海油气资源的开发[2-4]。目前国内外对水下管汇的损伤疲劳、动力响应等方面的研究寥寥无几，但对于管道碰撞的研究已有较为成熟的发展。Wierzbicki等[5]综合了管道初始轴向力对吸收能量和凹陷深度的影响关系，提出了管道的凹陷深度-吸收能量的经验公式，并对忽略剪切力作用下的情况提出了撞击力公式。Bai等[6]提出了圆形管道被挤压时挤压部位接触力的大小和弹性变形的对应关系。Katteland等[7]对水深较大海域中的海底管道受到坠落物撞击时的风险进行分析，并结合实例给出了几种不同坠落物体类型的荷载分布。Zeinoddini等[8]考虑到轴向预压的影响，结合数值模拟参数给出了侧向点荷载作用下的管线变形和破坏模式。Palmer等[9]在前人研究的基础上做了海底管道的碰撞实验，分析不同撞击能量吸收情况对海底管道碰撞后果评估的影响。Gaudin等[10]从岩土工程的观点出发，通过对管土相互作用的研究，可以协助设计管道的合理埋深。

基于对管道碰撞的研究方法，借助ANSYS/LS-DYNA建立水下管汇的三维碰撞模型，考虑海床土体的影响，模拟水下管汇受锚撞击的动态响应过程，分析水下管汇受锚击后的等效应力、应变以及凹陷损伤变形行为，可为水下管汇的安全运营提供理论依据。

1 锚-水下管汇有限元模型的建立

1.1 模型的几何参数及材料特性

文中建立的水下管汇模型是以某工程管汇为基础，经过简化得到。水下管汇模型分为两个部分：一是上部管道模型。海底管道尺寸参照海洋工程手册中关于我国海上油气田输油、输气和注水管道统计表进行选取，为方便区分将管道编号为1～6，管道的尺寸如表1表示；管道材料为X65钢，材料属性如表2所示，采用随动强化弹塑性模型模拟海底管道。二是下部基础桁架模型。对基础桁架模型，为方便网格划分，减少单元数量，进而缩短计算时间，桁架简化为交叉的长方体框架；文中使用双线性随动强化模型模拟基础桁架，桁架的材料属性如表3所示。

表1 管道尺寸表Tab. 1 Size of pipe

表2 管道的材料属性Tab. 2 Material parameters of pipe

表3 基础桁架的材料属性Tab. 3 Material parameters of basic truss

在分析水下管汇的碰撞问题时就要考虑管汇与海床土体之间的相互作用。本文建立的土体模型为黏性土，考虑到海床土体的性质，选用Drucker-Prager弹塑性有限元模型来模拟海床土体[11]，海床土体的D-P模型材料参数如表4所示。

表4 海床土体的D-P模型材料参数Tab. 4 Material parameters of the seabed 's D-P model

GB-T 546-1997规范中给出了霍尔锚的形状及尺寸，以GB-T 546-1997规范为依据，建立锚的模型。锚的材料为ZG200-400，采用双线性随动强化模型来模拟，锚的材料参数如表5所示。

表5 锚的材料参数Tab. 5 Material parameters of anchor

另外，将附加水质量以密度的形式加到锚上[12]。考虑附加水质量后的等效密度：

式中：ρe为考虑附加水质量后的等效密度，kg/m3;ρd为锚的密度，kg/m3；ρw为海水的密度，1025kg/m3；Ca是附加质量系数。

1.2 模型的建立

根据上节相关参数建立水下管汇的有限元模型如图1所示，管道采用SHELL163壳单元，设置管道的材料属性，建立管道单元模型；基础桁架采用SOLID164实体单元，设置桁架的材料属性，建立基础桁架模型；坠落物采用SOLID164实体单元，设置坠落物的材料属性，建立刚体模型；海床土体采用SOLID164实体单元，设置土体的材料属性，建立海床土体模型。

海床的边界条件：上表面为自由边界不定义约束，下表面固定垂向位移(RY=0)，侧面分别固定侧向位移，即与YOZ平面平行的面约束X方向位移(RX=0)、与XOY平行的面约束Z方向位移(RZ=0)。

图1 水下管汇的模型及网格Fig. 1 Model and mesh of submarine manifold

2 抛锚撞击水下管汇的结果分析

研究水下管汇受锚撞击后的动力响应，重点是分析水下管汇中管道的动力响应。管道动力响应过程中锚与管道垂直碰撞时的应力值最大[13]，因此在数值模拟时，假设锚从管汇正上方坠落。

DNV规范[14-15]指出：锚在水中的坠落速度取决于锚的形状和质量，并给出了锚在水中最终坠落速度的计算公式。根据DNV-RP-F107，物体下沉50～100 m时会达到一个终端速度，之后速度不再改变，该终端速度的计算公式：

式中：m为下沉物体的质量，kg；V为下沉物体的体积，m3；CD为阻力系数；A为下沉物体在流向上的投影面积；vT为终端速度。

根据式(2)可以得到在一定水深时抛出锚的终端速度，对于文中建立的锚模型，当1 000 kg的锚在水中下落，能够达到的最终坠落速度约为5 m/s。

2.1 管汇的mises应力时程分析

当锚的质量为1 000 kg，锚的坠落速度为5 m/s，水下管汇中的管道受撞击部位不同时刻的应力云图如图2所示。

图2 不同时刻水下管汇的应力云图Fig. 2 Stress of submarine manifold at different time

分析图2可知：锚最先与管道5开始接触，t=0.019 5 s，管道5的应力发生明显变化。锚继续下降，管道的应力不断增大，且应力区域沿管道6(管道4与管道5的连接管)的轴向扩展。t=0.021 s，管道5的应力达到第一个峰值(844.6 MPa)，此时，管道连接处的应力发生明显变化，在t=0.025 4 s达到最大值(最大应力693.5 MPa)。t=0.028 5 s，管道5的应力再次达到峰值(最大应力781.1 MPa)，应力的最大值出现在管道与锚的接触位置。

另外，应力沿管道5的轴向发展的同时，还沿管道6发展，但最大应力值小于撞击接触位置的最大应力值。因此，在整个撞击过程中，应力的最大值出现在锚与管道5的碰撞位置(如图3和图4所示)。

图3 水下管汇受撞击部位单元示意Fig. 3 The schematic diagram of the impact element of submarine manifold

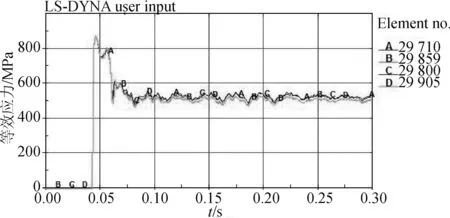
图4 水下管汇受撞击部位单元的等效应力Fig. 4 The equivalent stress of the impact element of submarine manifold

2.2 水下管汇凹陷变形时程分析

当锚的质量为1 000 kg，锚的坠落速度为5 m/s，水下管汇受锚撞击部位不同时刻的凹陷变形横截面图如图5所示。

图5 不同时刻水下管汇受撞击部位凹陷变形横截面图Fig. 5 Cross-section deformation of the impact site of submarine manifold in different time

图6 节点A、B示意图Fig. 6 The schematic diagram of nodes A and B

管汇受锚击后先发生弹性变形，随着锚继续下落，管汇的变形加剧，开始产生塑性变形。t=0.019 5 s时刻，锚与管汇开始接触，管汇开始产生明显变形；t=0.022 5 s，管汇变形首次达到一个峰值(11.2 mm)；一段时间后，锚与管汇慢慢发生分离，管汇上产生的弹性变形慢慢恢复，管汇的凹陷变形变小；t=0.03 s，由于管汇受撞击后，在竖直方向上会产生振动，锚与管汇发生二次接触，管汇的凹陷变形再次变大，达到新的峰值(12.2 mm)，短时间的接触后，锚与管汇再次分离，管汇的凹陷变形再次减小，渐渐趋于稳定。由于在管汇上产生的塑性变形是不可恢复的，最终在管汇的锚击部位会留下一个凹痕，最终凹陷变形深度为2.7 mm。

这里认为水下管汇的凹陷损伤深度为锚与水下管汇碰撞中心位置横截面的最上端的节点A与最下端的节点B的y方向的位移的差值(如图6～8所示)。

图7 节点A、B的垂向位移时程曲线Fig. 7 The vertical displacement time history curve of nodes A and B

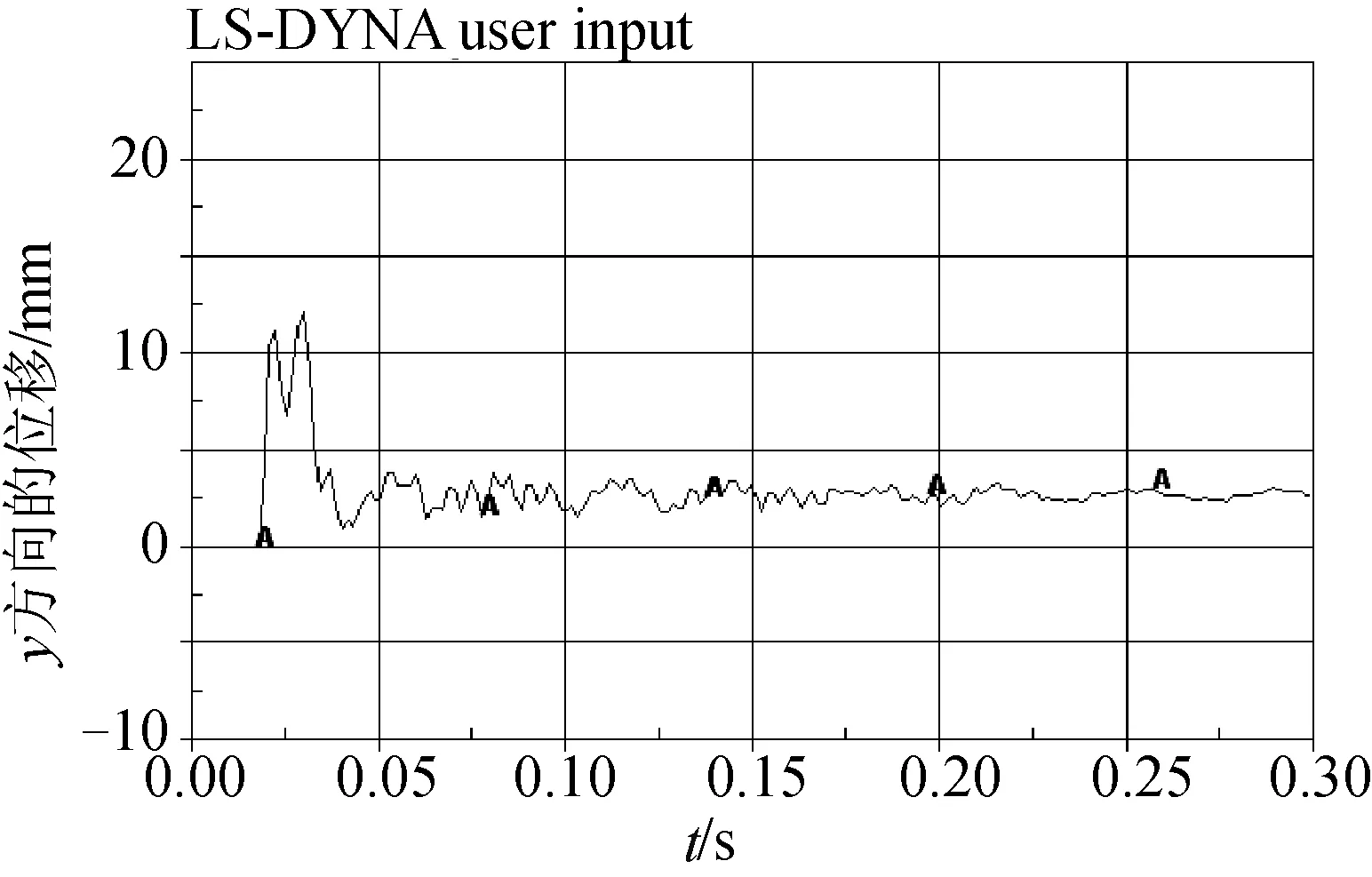
图8 节点A、B的垂向位移差值时程曲线Fig. 8 The vertical displacement difference between nodes A and B

2.3 锚与管汇接触面的形状对碰撞结果的影响

考虑锚与管汇接触面的形状对碰撞损伤的影响主要是通过改变锚的坠落角度来实现的，如图9是计算时考虑的三种锚与管汇接触面的形状。计算不同冲击能量下水下管汇的凹陷损伤深度及应力，计算结果如图10所示。

图9 锚与管汇接触面的三种形状Fig. 9 The interface’s shape between the anchor and manifold

当冲击能量为2 kJ，锚与管汇接触为形状一时，造成水下管汇的凹陷损伤深度为0.2 mm；锚与管汇接触面为形状二时，造成水下管汇的凹陷损伤深度为0.3 mm；锚与管汇接触面为形状三时，造成水下管汇的凹陷损伤深度为3.2 mm。

当冲击能量为12.5 kJ，锚与管汇接触面为形状一时，造成水下管汇的凹陷损伤深度为1.2 mm；锚与管汇接触面为形状二时，造成水下管汇的凹陷损伤深度为2.7 mm；锚与管汇接触面为形状三时，造成水下管汇的凹陷损伤深度为6.9 mm。

当冲击能量为24.5 kJ，锚与管汇接触面为形状一时，造成水下管汇的凹陷损伤深度为3.3 mm；锚与管汇接触面为形状二时，造成水下管汇的凹陷损伤深度为7.0 mm；锚与管汇接触面为形状三时，造成水下管汇的凹陷损伤深度为17.5 mm。

由此可得：在同一冲击能量下，锚与管汇接触面为形状三时对水下管汇的损伤最大，锚与管汇接触面为形状二时次之，锚与管汇接触面为形状一时最小。这是因为锚与水下管汇的接触面积越小，水下管汇损伤面积越小，损伤深度就越大。

另外，从图10中还可以得到：锚与管汇接触面的形状相同时，冲击能量越大，水下管汇的损伤变形越大。

在撞击过程中，当应力的最大值大于管材的屈服强度448 MPa时，就会产生塑性变形。针对三种锚与管汇的接触面形式，分别计算不同冲击能量对管汇的最大应力的影响，比较不同碰撞接触面下，应力最大值达到管汇的屈服强度448 MPa所需要的冲击能量，计算结果如图11所示。

当锚与管汇接触面为形状一时，应力最大值达到管汇的屈服强度448 MPa对应的冲击能量为1.13 kJ；当锚与管汇接触面为形状二时，应力最大值达到管汇的屈服强度448 MPa对应的冲击能量为0.76 kJ；当锚与管汇接触面为形状三时，应力最大值达到管汇的屈服强度448 MPa对应的冲击能量为0.55 kJ。

由此可得：在碰撞过程中，锚与管汇接触面为形状三时，水下管汇的应力达到屈服强度所需要的冲击能量最小，最易发生塑性变形；锚与管汇接触面为形状二时次之，锚与管汇接触面为形状一时所需要的冲击能量最大。

图10 接触面形状对管汇损伤深度的影响Fig. 10 The influence of the interface’s shape on the manifold damage depth

图11 最大等效应力随冲击能量变化图Fig. 11 The maximum equivalent stress with impact energy change

2.4 海床土体对碰撞的影响

2.4.1 海床土体的剪切弹性模量影响分析

剪切弹性模量是指在弹性变形比例极限范围内，切应力与切应变的比值。剪切弹性模量越大，则表示土体的刚性越强。

分别取不同的海床土体的剪切弹性模量，冲击能量为12.5 kJ、24.5 kJ及100 kJ时，管汇的凹陷损伤深度及最大等效应力的计算结果如图12和图13所示。

冲击能量为12.5 kJ：海床土体的剪切弹性模量为5 MPa时，管汇的凹陷损伤深度为2.75 mm，最大等效应力为831.6 MPa；海床土体的剪切弹性模量为15 MPa时，管汇的凹陷损伤深度为2.75 mm，最大等效应力为831.6 MPa；当海床土体的剪切弹性模量为25 MPa时，管汇的凹陷损伤深度为2.75 mm，最大等效应力为832.2 MPa。

图12 剪切弹性模量对凹陷损伤深度的影响Fig. 12 The effect of shear elastic modulus on the depth of the dent damage

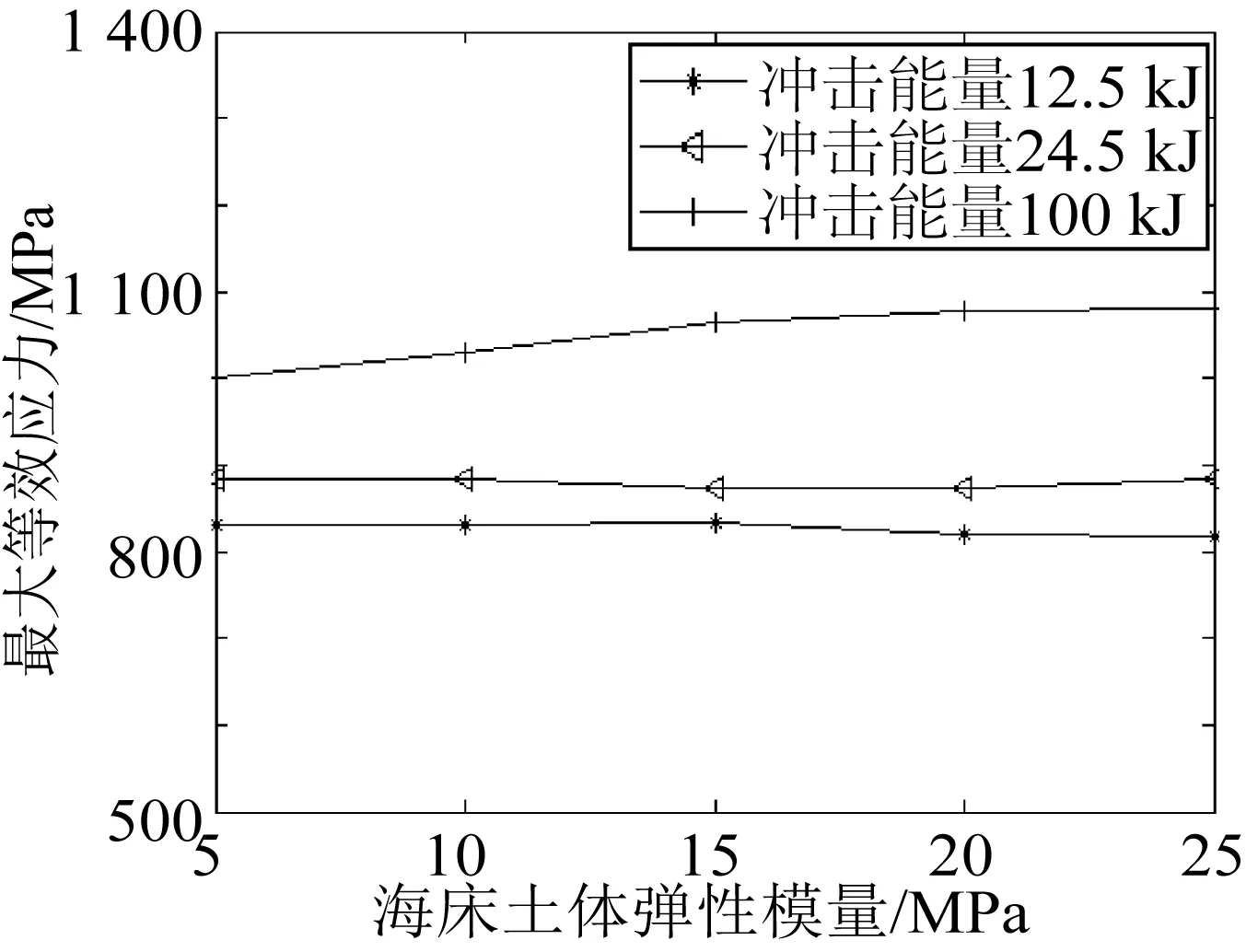
图13 剪切弹性模量对最大等效应力的影响Fig. 13 The effect of shear elastic modulus on the maximum equivalent stress

冲击能量为24.5 kJ：海床土体的剪切弹性模量为5 MPa时，管汇的凹陷损伤深度为7.05 mm，最大等效应力为883.13 MPa；海床土体的剪切弹性模量为15 MPa时，管汇的凹陷损伤深度为7.1 mm，最大等效应力为883.09 MPa；当海床土体的剪切弹性模量为25 MPa时，管汇的凹陷损伤深度为7.1 mm，最大等效应力为883.32 MPa。

冲击能量为100 kJ：海床土体的剪切弹性模量为5 MPa时，管汇的凹陷损伤深度为41.15 mm，最大等效应力为1 000.49 MPa；海床土体的剪切弹性模量为15 MPa时，管汇的凹陷损伤深度为41.975 mm，最大等效应力为1064.3 MPa；海床土体的剪切弹性模量为25 MPa时，管汇的凹陷损伤深度为42.6 mm，最大等效应力为1 079.3 MPa。

由此可知：冲击能量较小时，伴随海床土体的剪切弹性模量的增大，管汇的凹陷损伤深度和管汇的最大等效应力的变化较小，而冲击能量较大时，管汇的凹陷损伤深度和管汇的最大等效应力随海床土体的剪切弹性模量的增大而增大。

2.4.2 海床土体的内摩擦角影响分析

保持土体的其他参数不变，分别取不同海床土体的内摩擦角，冲击能量为12.5 kJ、24.5 kJ及100 kJ时，管汇的凹陷损伤深度及最大等效应力的计算结果如图14和图15所示。

冲击能量为12.5 kJ：海床土体的内摩擦角为5°时，管汇的凹陷损伤深度为2.7 mm，最大等效应力为844.61 MPa；海床土体的内摩擦角为20°时，管汇的凹陷损伤深度为2.7 mm，最大等效应力为844.61 MPa；海床土体的内摩擦角为40°时，管汇的凹陷损伤深度为2.7 mm，最大等效应力为844.61 MPa。

冲击能量为24.5 kJ：海床土体的内摩擦角为5°时，管汇的凹陷损伤深度为7.0 mm，最大等效应力为872.5 MPa；海床土体的内摩擦角为20°时，管汇的凹陷损伤深度为7.0 mm，最大等效应力为872.5 MPa；海床土体的内摩擦角为40°时，管汇的凹陷损伤深度为7.0 mm，最大等效应力为872.5 MPa。

冲击能量为100 kJ：海床土体的内摩擦角为5°时，管汇的凹陷损伤深度为41.975 mm，最大等效应力为1 064.1 MPa；海床土体的内摩擦角为20°时，管汇的凹陷损伤深度为41.975 mm，最大等效应力为1 064.1 MPa；海床土体的内摩擦角为40°时，管汇的凹陷损伤深度为41.975 mm，最大等效应力为1 064.1 MPa。

由此可知：对于黏性土而言，伴随海床土体内摩擦角的增大，管汇的凹陷损伤深度及最大等效应力值的变化较小。

图14 内摩擦角对凹陷损伤深度的影响Fig. 14 The effect of internal friction angle on the depth of the dent damage

图15 内摩擦角对最大等效应力的影响Fig. 15 The effect of internal friction angle on the maximum equivalent stress

3 结 语

基于ANSYS/LS-DYNA动力学分析软件，建立锚-管汇-海床土体的碰撞计算模型。分析了管汇受坠物冲击时等效应力和变形的变化情况，最大等效应力点出现在管汇与锚接触位置处，管汇受撞击后，锚与管汇的接触位置会发生明显的变形，最终在管汇上留下变形凹痕。锚与水下管汇的碰撞接触面积越小，水下管汇的损伤深度就越大，且水下管汇的应力达到屈服强度所需要的冲击能量也越小，即越易发生塑性变形。锚与管汇接触面的形状相同时，冲击能量越大，水下管汇的损伤变形越大。冲击能量较小时，海床土体的剪切弹性模量对管汇的凹陷损伤深度以及最大等效应力影响较小，而冲击能量较大时，管汇的凹陷损伤深度和管汇的最大等效应力随海床土体的剪切弹性模量的增大而增大。对于黏性土体而言，海床土体的内摩擦角对管汇的碰撞影响作用非常微弱。

[1] 张瑾，谢毅. 深水水下管汇安装方法研究与进展[J]. 海洋工程，2011，29(2)：143-148. (ZHANG Jin, XIE Yi. Research and development of the method for the installation of submarine manifold in deep water[J]. The Ocean Engineering,2011,29(2):143-148. (in Chinese))

[2] 王进全，王定亚. 国外海洋钻井隔水管与国产化研究建议[J]. 石油机械，2009，37(9)：147-150 .(WANG Jinquan,WANG Dingya. Suggestions on the research of offshore drilling riser and localization in foreign countries[J]. China Petroleum Machinery, 2009,37(9):147-150.(in chinese))

[3] 王玮，孙丽萍，白勇. 水下油气生产系统[J]. 中国海洋平台，2009，24(6)：41-45. (WANG Wei, SUN Liping, BAI Yong. Submarine oil and gas production system[J]. China Offshore Platform,2009,24(6):41-45. (in Chinese))

[4] 李清平. 我国海洋深水油气开发面临的挑战[J]. 中国海上油气，2006，18(2)：130-133. (LI Qingping. The challenge to the development of offshore deepwater oil and gas in China[J]. China Offshore Oil and Gas,2006,18(2):130-133. (in Chinese))

[5] WIERZBICKI T, SUH M S. Indentation of tubes under combined loading[J]. International Journal of Mechanical Sciences, 1988, 229-248.

[6] BIA Y, PEDRSEN P T. Elastic-plastic behaviour of offshore steel structures under impact loads[J]. International Journal of Impact Engineering, 1993, 13:99-115.

[7] KATTELAND L H, OEYGARDEN B. Risk analysis of dropped objects for deep water development[C] //Proceedings of International Conference on Offshore Mechanics and Artic Engineering. 1995:R45865.

[8] ZEINODDINI M, HARDING J E, PARKE G A R. Effect of impact damage on the capacity of tubular steel members of offshore structures[J]. Marine Structures, 1998,11: 141-157.

[9] PALMER A, TOUHEY M, HOLDER S, et al. Full-scale impact tests on pipelines[J]. International Journal of Impact Engineering, 2006, 32:1267-1283.

[10] GAUDIN C, VLAHOS G, RANDOLPH M F, et al. Investigation in centrifuge of anchor-pipeline interaction[J]. International Journal of Offshore and Polar Engineering, 2007,17:67-73.

[11] 白俊磊.海底管道坠物碰撞损伤数值模拟分析研究[D]. 大连：大连理工大学，2013. (BAI Junlei. Numerical simulation and analysis of the impact damage of submarine pipeline with falling objects[D]. Dalian:Dalian University of Technology,2013. (in Chinese))

[12] 王自力，蒋志勇，顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击，2002，22(4)：321-326. (WANG Zili, JIANG Zhiyong, GU Yongning. The additional mass model for numerical simulation of ship collision[J]. Explosion and Impact,2002,22(4): 321-326. (in Chinese))

[13] 杨秀娟，修宗祥，闫相祯,等. 海底管道受坠物撞击的三维仿真研究[J]. 振动与冲击，2009，28(11)：47-50. (YANG Xiujuan, XIU Zongxiang, YAN Xiangzhen,et al. The 3D simulation of submarine pipeline impacted by dropped objects[J]. Vibration and Impact,2009,28(11):47-50. (in Chinese))

[14] DNV-RP-F107, Risk assessment of pipelines protection[S]. Oslo: Det Norske Veritas Classification A/5, 2010.

[15] DNV OS F101-1996, Rules for submarine pipeline systems[S]. Oslo:Det Norske Veritas Classification A/S, 1996.

Numerical simulation of anchor impacting submarine manifold

LOU Min1, WANG Yanhong1, MING Haiqin2

(1. College of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China; 2. CIMC Raffles Offshore Engineering Co.， Ltd., Yantai 264000, China)

1005-9865(2016)04-0038-09

P756.2

A

10.16483/j.issn.1005-9865.2016.04.006

2015-07-11

国家自然科学基金(51309241，51579245)

娄 敏(1981-)，女，博士，副教授，主要从事海底管道设计、建造及在位研究。E-mail:shidaloumin@163.com