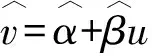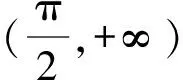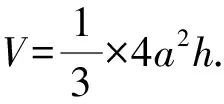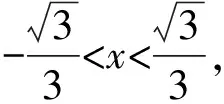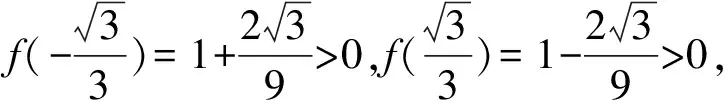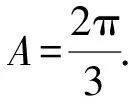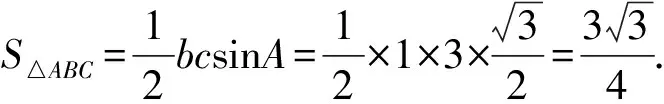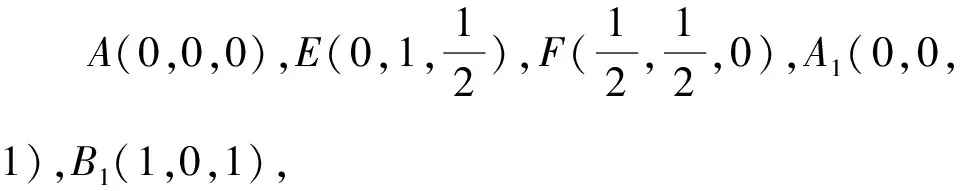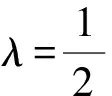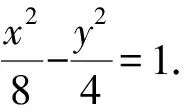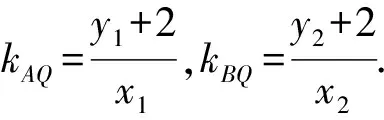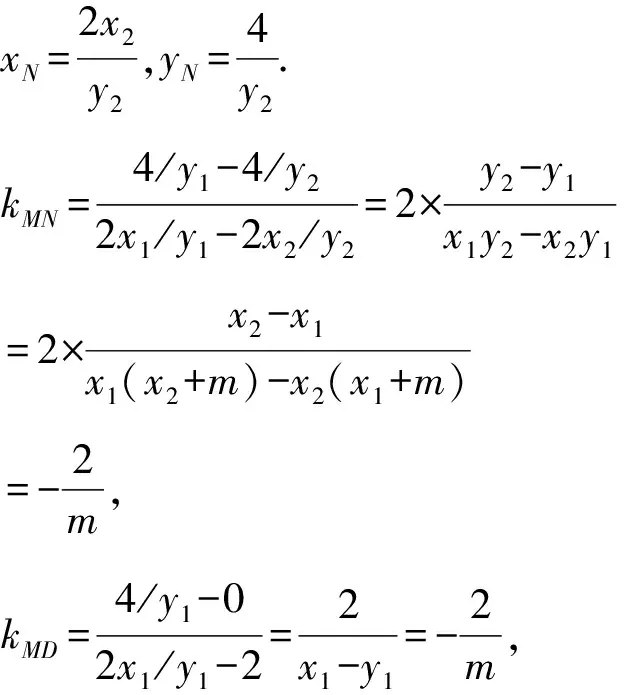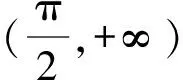2024年普通高等学校招生全国统一考试数学新高考Ⅰ卷模拟试卷
2024-03-06李昌成
李昌成
(乌鲁木齐市第八中学,新疆 乌鲁木齐 830002)
一、单选题:本大题共8小题,共40.0分.在每小题列出的选项中,选出符合题目的一项.
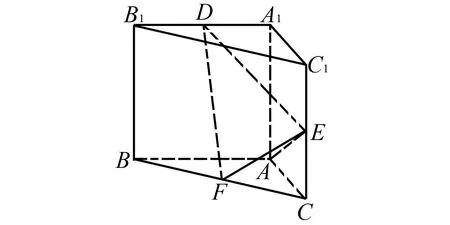
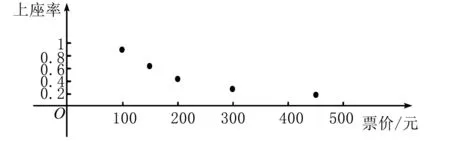
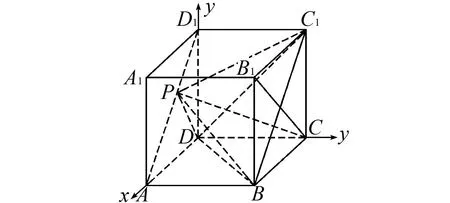
1.设集合U=R,A={x|1 A.{x|x≥2} B.{x|x≤2} C.{x|1 图1 第1题图 A.-1+i B.1-i C.1+i D.-1-i 4.已知三棱台ABC-A1B1C1中,三棱锥A-A1B1C1的体积为4,三棱锥A1-ABC的体积为8,则该三棱台的体积为( ). 5.从装有3个红球、2个白球的袋中任取2个球,则所取的2个球中至少有1个白球的概率是( ). 6.已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图2所示,则下列判断错误的是( ). A.函数f(x)的最小正周期为2 B.函数f(x)的值域为[-4,4] 图2 第6题图 7.若a>b>1,0 A.ac C.abc 8.某四棱锥的底面为正方形,顶点在底面的射影为正方形中心,该四棱锥内有一个半径为1的球,则该四棱锥的表面积的最小值是( ). A.16 B.8 C.32 D.24 9.如图3,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段AD1上的动点,则下列命题正确的是( ). A.异面直线C1P与CB1所成角的大小为定值 B.三棱锥D-BPC1的体积是定值 C.直线CP和平面ABC1D1所成的角的大小是定值 D.若点Q是线段BD上动点,则直线PQ与A1C不可能平行 图3 第9题图 10.已知函数f(x)=x3-x+1,g(x)=f(x)-ax(a∈R),则( ). A.f(x)有两个极值点 B.f(x)的图象与x轴有三个交点 C.点(0,1)是曲线y=f(x)的对称中心 D.若g(x)存在单调递减区间,则a≥-1 11.已知抛物线C:x2=2y的焦点为F,准线为l,A,B是C上的两点,O为坐标原点,则( ). A.l的方程为y=-1 B.若方程kf(x)=x2恰好只有一个实数根,则k<0 C.若x1>x2>0,总有m[g(x1)-g(x2)]>f(x1)-f(x2)恒成立,则m≥1 13.(x2-x+2)5的展开式中x3的系数为____. 14.已知圆C:x2+y2-4x-2y+1=0,点P是直线y=4上的动点,过P作圆的两条切线,切点分别为A,B,则|AB|的最小值为____. 15.已知函数f(x)=x3+mx,若f(ex)≥f(x+1)对x∈R恒成立,则实数m的取值范围为____. 17.已知数列{an}满足a1=1,an+1=an+2,数列{bn}的前n项和为Sn,且Sn=2-bn. (1)求数列{an},{bn}的通项公式; (2)设cn=an+bn,求数列{cn}的前n项和Tn. (1)求△ABC外接圆的半径; (2)若c=3,求△ABC的面积. 19.如图4,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点. 图4 第19题图 (1)证明:DF⊥AE; 20.某剧场的座位数量是固定的,管理人员统计了最近在该剧场举办的五场表演的票价xi(单位:元)和上座率yi(上座人数与总座位数的比值)的数据,其中i=1,2,3,4,5,并根据统计数据得到如图5的散点图: 图5 第20题图 (1)由散点图判断y=bx+a与y=clnx+d哪个模型能更好地对y与x的关系进行拟合(给出判断即可,不必说明理由),并根据你的判断结果求回归方程; (2)根据(1)所求的回归方程,预测票价为多少时,剧场的门票收入最多. (1)求双曲线C的方程; (2)已知Q(0,-2),D为PQ的中点,作PQ的平行线l与双曲线C交于不同的两点A,B,直线AQ与双曲线C交于另一点M,直线BQ与双曲线C交于另一点N,证明:M,N,D三点共线. 22.已知函数f(x)=aln(x+1)-sinx. 参考答案 1.由Venn图可知,阴影部分的元素由属于集合A但不属于集合B的元素构成,所以阴影部分表示的集合为A∩(UB).因为集合U=R,A={x|1 故选D. 故选B. 图6 第3题解析图 故选B. 故选B. 故选C. 故选D. 7.因为a>b>1,0 因为a>b>1,0 即alogbc 因为a>b>1,0 即abc>bac,故C错误. 因为a>b>1,0 故选B. 设t=h-2>0,可得h=t+2. 故选C. 9.因为CB1⊥BC1,CB1⊥AB,BC1∩AB=B,所以CB1⊥平面ABC1D1.又C1P⊂平面ABC1D1,得CB1⊥C1P,所以异面直线C1P与CB1垂直,选项A正确.三棱锥D-BPC1以BDC1为底面,因为AD1∥平面BDC1,所以点P到平面BDC1的距离为定值,故三棱锥D-BPC1的体积是定值,选项B正确. 点C在平面ABC1D1的射影是定点(BC1与B1C的交点),线段CP长度显然随位置变化而变化,故直线CP和平面ABC1D1所成的角的正弦在变化,角的大小不是定值,选项C错误. 故选AB. 图7 第9题解析图 10.已知f(x)=x3-x+1,则f′(x)=3x2-1. 令f′(x)=3x2-1=h(x),得h′(x)=6x=0,得x=0,此时f(0)=1,得曲线y=f(x)的对称中心为(0,1),故C项正确. 由g(x)=f(x)-ax,得g′(x)=f′(x)-a=3x2-1-a,若g(x)存在单调递减区间,即g′(x)<0有解,得a>3x2-1有解,等价于a>(3x2-1)min,则a>-1,故D项错误. 故选AC. 故选BC. 图8 第11题解析图 图9 第12题解析图 故选ACD. 14.圆C:x2+y2-4x-2y+1=0, 即(x-2)2+(y-1)2=4. 图10 第14题解析图 如图10,由于PA,PB分别切圆C于点A,B,则|PA|=|PB|,CA⊥PA,CB⊥PB,所以S四边形APBC=2S△ACP=|CA|·|PA|. 因为|CA|=|CB|=r=2,所以S四边形APBC=2|PA|. 所以|AB|最短时,|CP|最短,点C到直线y=4的距离即为|CP|的最小值,所以|CP|min=3. 15.令y=ex-(x+1),所以y′=ex-1.显然当x>0时,y′>0,则y在(0,+∞)上单调递增;当x<0时,y′<0,则y在(-∞,0)上单调递减.即x=0时取得最小值ymin=0,故ex≥x+1恒成立. 若f(ex)≥f(x+1)对x∈R恒成立,则f(x)在R上单调递增,则f′(x)≥0恒成立,f′(x)=3x2+m≥0,m≥-3x2,又(-3x2)max=0,故m≥0. 故答案为[0,+∞). (1+4k2)x2+8kbx+4b2-4=0. 如图11,因为直线l与椭圆E相切,所以△=(8kb)2-4(4k2+1)(4b2-4)=0,解得4k2=b2-1. 图11 第16题解析图 即m=2n. 17.(1)由题知,a1=1,an+1-an=2,所以数列{an}是首项为1,公差为2的等差数列. 所以an=1+(n-1)×2=2n-1. 当n=1时,b1=S1=2-b1,所以b1=1. 当n≥2时,Sn=2-bn, ① Sn-1=2-bn-1. ② 由①-②,得bn=-bn+bn-1. 利用分组求和可得, 整理,得b2+c2-a2=-bc. 所以由余弦定理,得 解得b=1或b=-4(舍). 19.(1)因为AE⊥A1B1,A1B1∥AB, 所以AE⊥AB. 又因为AA1⊥平面ABC,AB⊂平面ABC, 所以AA1⊥AB. 又AA1∩AE=A,AA1,AE⊂平面A1ACC1, 所以AB⊥平面A1ACC1. 图12 第19题解析图 又因为AC⊂平面A1ACC1,所以AB⊥AC. 所以AB,AC,AA1两两垂直. 所以DF⊥AE. 令x=3,则y=1+2λ,z=2(1-λ). 则n=(3,1+2λ,2(1-λ)). 所以当D为A1B1中点时满足要求. 20.(1)y=clnx+d能更好地对y与x的关系进行拟合. 设z=lnx,先求y关于z的线性回归方程. 所以y关于x的回归方程为y=-0.5lnx+3.2. (2)设该剧场的总座位数为M,由题意得门票收入为M(-0.5xlnx+3.2x),设函数f(x)=-0.5xlnx+3.2x,则f′(x)=-0.5lnx+2.7,当f′(x)<0,即x>e5.4时,函数单调递减,当f′(x)>0,即0 故预测票价为220元时,剧场的门票收入最多. (2)因为P(4,2),Q(0,-2),D为PQ的中点,所以D(2,0),kPQ=1. 设直线l的方程为y=x+m,A(x1,y1),B(x2,y2),M(xM,yM),N(xN,yN), 所以kMN=kMD. 故M,N,D三点共线. 22.(1)由题意得:函数定义域为(-1,+∞). 令g(x)=(x+1)cosx,则 g′(x)=cosx-(x+1)sinx. g′(x)=cosx[1-(x+1)·tanx]. 所以a≤[g(x)]min=0. 即a的取值范围为(-∞,0]. 当x>e-1时,ln(x+1)>lne=1≥sinx,所以f(x)>0在(e-1,+∞)上恒成立. f(e-1)=1-sin(e-1)>0,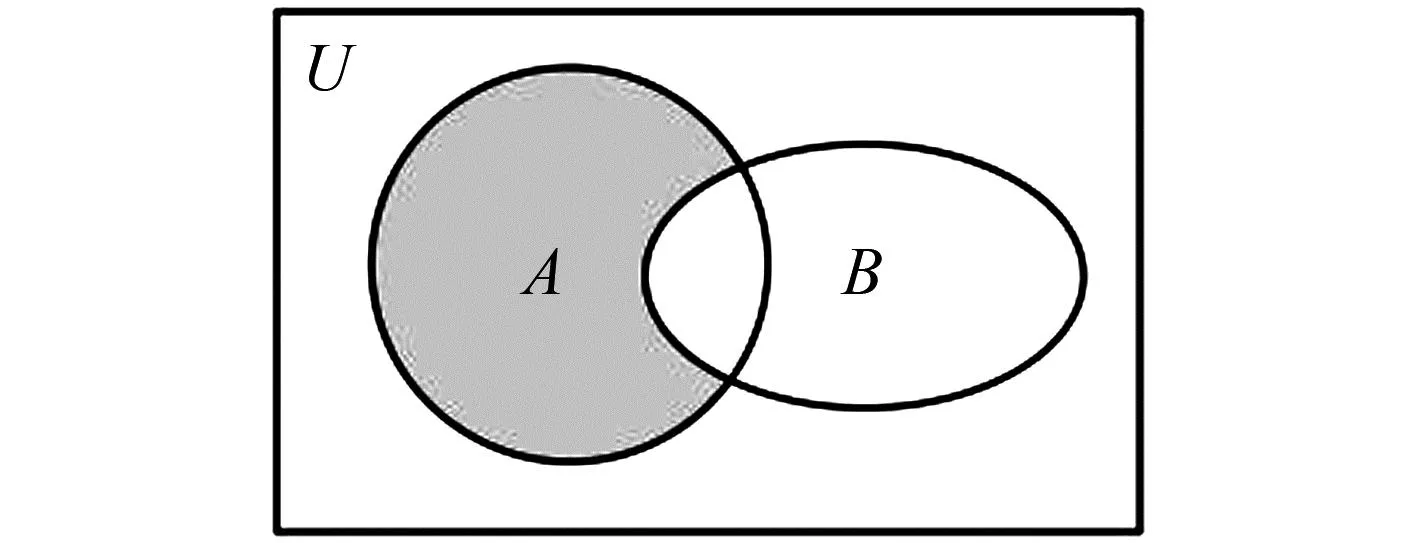





二、多选题:本大题共4小题,共20.0分.在每小题有多项符合题目要求.
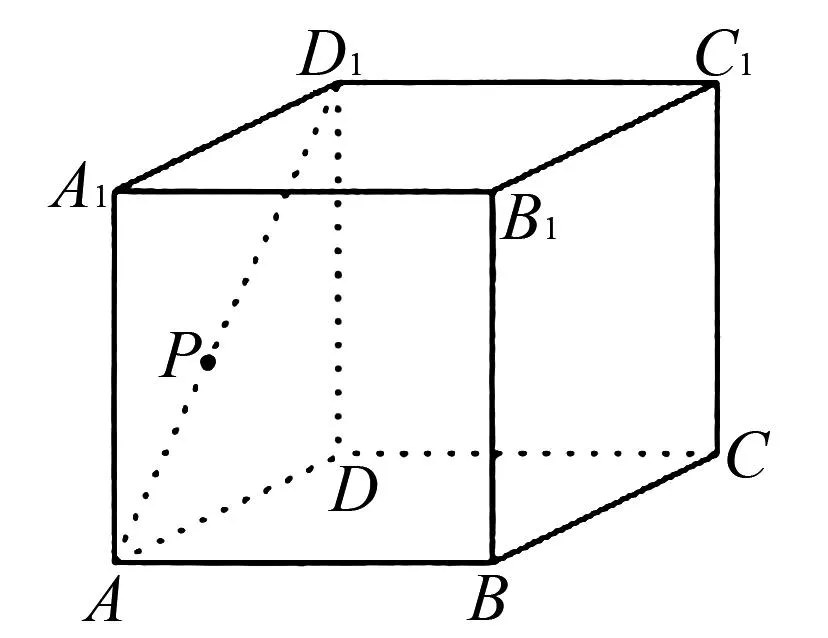
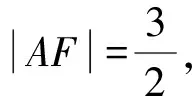

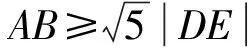

三、填空题:本大题共4小题,共20.0分

四、解答题:本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤.