多用户MIMO-MEC网络中基于APSO的任务卸载研究

顾 敏，徐雅男，王辛迪，花 敏，周 雯*

(1.南京林业大学 信息科学技术学院，江苏 南京 210037；2.安徽大学 互联网学院，安徽 合肥 230039)

0 引言

随着5G移动通信技术的发展,计算密集型应用以及物联网(Internet of Things, IoT)相关应用迅速增加,给智能终端设备和中心网络的实时处理带来了巨大挑战[1]。传统模式下的任务计算卸载模式如云计算、雾计算等,难以高效地执行计算密集型任务,导致用户的体验质量(Quality of Experience, QoE)下降。为了缓解这一困难,移动边缘计算(Mobile Edge Computing, MEC)应运而生。MEC系统允许设备将计算任务卸载到网络边缘节点,如基站、无线接入点等,既满足了终端设备计算能力的扩展需求,同时弥补了云计算时延较长的缺点[2]。

为了发挥边缘计算技术在缓解移动终端计算资源不足和降低终端时延[3]、能耗[4-5]等方面的优势,必须采用有效的任务决策及资源管理策略。文献[3-9]对单天线边缘计算系统的任务卸载问题进行了研究。文献[7]研究了时延和能量损耗的权衡关系,提出一种基于MEC的内容感知分类卸载算法。文献[8]提出了多小区MEC系统的能量感知任务卸载方案,在有限的能量和敏感的延迟下联合优化了通信和计算资源的分配。文献[9-12]对多天线边缘计算系统的任务卸载进行研究。文献[9]在MEC系统引入了多输入多输出(Multiple Input Multiple Output, MIMO)技术,对系统具备完全信道信息(Channel State Information, CSI)和不完全CSI这2种情况下的任务卸载问题分别进行了研究。文献[11]考虑了无线、计算、回程和上下行资源分配的联合优化,提出了一种基于连续凸逼近的迭代算法。文献[12]研究了具有无线回程的2层海量MIMO异质网络中的节能资源分配问题。

现有基于MEC的MIMO多用户系统的研究通常假设基站是多天线,用户端是单天线[9,12-13],而对于用户端是多天线的研究较少。同时很多研究假设下行链路的反馈结果很小,将反馈时延予以忽略,未考虑到下行链路中多路数据的传输。另一方面,文本、视频和图像均可采用数据压缩技术进行压缩,减小传输的数据量。本文在MIMO-MEC系统引入该技术,以期降低系统运算成本。

基于上述,本文研究了具备数据压缩功能的MEC系统的任务决策问题,其中基站、多用户均配备了多根天线。该问题可以归结为一个非凸的多约束优化问题。考虑到粒子群算法可解决复杂的多约束目标优化问题,文献[14-16]将其用来解决MEC系统的任务卸载及资源分配问题,本文基于改进的粒子群算法提出了一种多用户任务分配算法,对上行链路的带宽、发送功率和压缩比例等多个方面进行了优化。仿真结果表明,提出的方法优于若干对比方案,能够有效降低任务的执行时延。

1 系统模型

如图1所示,MIMO-MEC网络由K个用户设备(User Equipment,UE)和一个基站(Base Station,BS)组成,且基站配备一个MEC服务器。用户和BS均配备多根天线:BS配有NT根天线,用户k配备NR,k根天线,∀k∈≜{1,2,…,K}。在此系统中,UE的任务可以一部分在本地执行计算,另外一部分可以卸载到MEC服务器进行计算。为了节省数据传输量,卸载的任务可以先进行部分压缩再上传至MEC服务器计算。

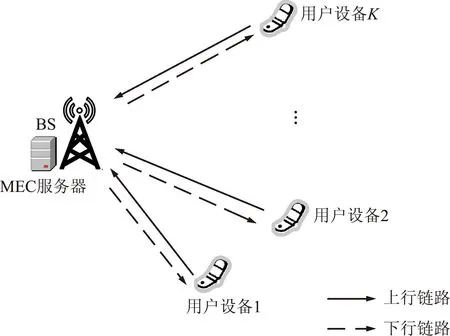
图1 MEC的MIMO网络框架Fig.1 MIMO network framework for MEC

如图2所示,用户i的任务卸载过程分为3个环节:本地处理、上行链路传输计算和下行链路反馈。首先,将任务拆分,其中一部分用于本地计算,剩余任务按比例压缩处理并在任务结束后上传至MEC服务器,此时未压缩任务卸载到MEC服务器中计算;其次,当压缩任务传输完成并且未压缩任务也计算完毕,MEC服务器开始处理压缩任务,即解压任务并计算;最后,MEC服务器将计算数据反馈到用户,并与本地计算的结果进行组合,此时用户i的计算任务处理完毕。

图2 任务卸载过程Fig.2 Task offloading process

多用户在上下行链路的通信采用频分复用(Frequency Division Multiple Access,FDMA)的方式并行处理,各个用户互不干扰。

本文对任务的卸载比例、压缩比例和用户发送功率等多个参数进行联合优化,目标是最小化多用户任务的总时延。接下来,分别对通信模型和任务卸载模型做进一步解释,最后将问题归结为多约束的优化问题。

1.1 通信模型

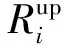
(1)

(2)

(3)

(4)

式中:Bmax和B′max分别是上行链路和下行链路的总带宽。本文对用户的上行链路带宽进行优化,对下行链路带宽采用平均分配方式。

(5)

1.2 计算模型

本节详细描述用户i的任务卸载过程。如前所述,用户i的计算任务表示为i={Di,Ci,Ji,Li,ρi},假设计算任务可按比例任意切割,任务卸载比例αi∈[0,1],0代表用户任务完全由本地执行,1代表用户任务完全卸载到MEC服务器执行。卸载的任务αiDi进行部分压缩,压缩比例βi∈[0,1],0代表卸载任务不压缩执行,1代表任务全部压缩卸载到MEC服务器执行。进一步假设,任务压缩前后数据量的比率为γi∈[0,1],则卸载任务中未压缩的数压缩的数据量为αiDiβiγi。

(6)

(7)

式中:Fi为用户设备UEi的计算频率。由于压缩和任务执行是并行的,所以本地计算的总时延为:

(8)

(9)

(10)

因此总能耗为:

(11)

(12)

(13)

(14)

(15)

根据图2不难发现,用户i的任务卸载总时延(不包括结果反馈时延)为:

(16)

(17)

(18)

因此,用户的总能耗为:

(19)

注意,在计算能耗时,本文仅考虑用户的能耗,不考虑MEC的能耗。

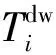
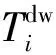
(20)

(21)

式中:ηi∈(0,1]表示MEC计算结果与卸载任务数据量的比率。

根据上述分析,用户i卸载计算的总时延Ti可以表示为:

(22)

用户i的总能耗为:

(23)

1.3 问题模型

本文的目标是最小化所有用户的任务执行时延之和,优化变量包括:①任务的卸载比例;②卸载任务的压缩比例;③用户发送功率;④任务的计算频率;⑤上行信道的用户带宽。

将当前问题联合表达为:

(24)

在P1中,约束条件C1表示UE的能耗不超过最大能耗阈值;C2表示MEC给UE的计算资源不超过自身最大计算资源;C3表示MEC分配给UE集合的计算资源不超过自身最大计算资源;C4表示UE的信道带宽不超过小区设置的通信带宽最大值;C5表示UE的信道带宽集合不超过小区设置的通信带宽最大值; C6、C7和C8分别表示了UE任务卸载比例、卸载任务中选取压缩部分的比例以及传输功率的取值范围。

此外,本文涉及变量较多,为了方便阅读,系统模型涉及的主要变量如表1所示。

表1 系统模型中的符号含义Tab.1 Notations’ meanings in the system model

2 算法设计

近年来,群智能算法如遗传算法[18-20]、蚁群算法[21]等受到了研究者的关注,已经应用到了图像处理、网络资源分配等方面。粒子群优化 (Particle Swarm Optimization,PSO) 算法属于群智能算法的一种,是通过模拟鸟群捕食行为设计的。算法采用“群体”与“进化”的概念,从随机解出发,依据个体的适应度通过迭代寻找最优解。传统PSO算法采用固定的惯性权重,存在早熟收敛、易陷入局部最优等缺点;而自适应粒子群优化(Adaptive Particle Swarm Optimization,APSO)算法通过自适应地调整惯性权重来提高寻优能力和收敛能力。基于APSO算法框架,本节提出了多用户多任务的卸载算法。

2.1 自适应权重粒子群算法[21]

惯性权重是PSO算法中调节局部搜索和全局搜索的关键参数。惯性权重值越大,收敛速度越快,全局搜索能力强而局部搜索能力弱。APSO对传统PSO算法的惯性权重进行了改进,使粒子群的运动速度随系统环境的变化而变化,可以部分克服传统粒子群算法容易陷入局部最优解的缺点。粒子群能对全局进行充分探测[22],从而提高粒子的全局搜索能力。惯性权重ω的设置如下:

(25)

式中:fj为粒子j的当前适度值,favg和fmax分别为种群粒子的平均适应度值和最大适应度值。适应度越小,说明距离最优解越近,此时更需要局部搜索;适应度越大,说明距离最优解越远,此时需要全局搜索。与传统PSO算法相比,APSO的惯性权重与迭代次数及每个粒子的适应度均相关[21]。

2.2 提出的多用户多任务卸载算法

本节首先构造适应度函数,然后基于APSO提出多用户多任务的MEC卸载算法。

①适应度函数:观察P1可知约束条件C1过于复杂,为了简化求解,将C1并入目标函数中。采用罚函数法,构造粒子的适应度函数如下:

(26)

式中:x代表某粒子。

Penl是惩罚函数,定义为:

(27)

式中:λ>0是惩罚因子。

基于上述适应度函数,构造问题P2:

(28)

根据文献[23],P2与P1是等价的。

②MEC卸载算法:为了求解P2,基于APSO算法提出多用户任务卸载算法。算法的每个粒子表示问题的一种潜在解。在5K维解空间中,第j个粒子在第k次迭代中的位置和速度可以表示为:

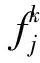
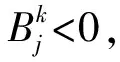
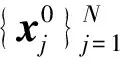
⑤迭代指数k≐k+1;

⑥判断问题的解是否收敛,若收敛则结束循环,输出结果,否则转到②。

上述提出的卸载算法可以优化卸载比例、压缩比例及带宽等参数,通过不断迭代最终获得最优或者次优解。

2.3 算法复杂度分析

假设一次乘法或者除法的运算量为O(1)。首先,应根据式(1)和式(2)计算上、下行传输速率。考虑到n维矩阵行列式运算的复杂度为O(n3)以及m×n维矩阵SVD分解的复杂度为O(mn2),这一环节的运算量为:

(33)

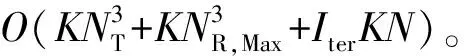
3 仿真结果与分析

为了检验MEC-MIMO网络中提出的APSO卸载策略的性能,本节首先对算法的收敛性进行分析,其次从用户设备、任务强度和任务数据大小3个方面对5种计算卸载策略的资源分配算法进行系统任务执行时延的对比,所有策略包括:基于标准的PSO算法的MEC计算卸载(记为PSO)、基于APSO算法的MEC计算卸载(记为APSO)、基于APSO算法数据不压缩的MEC计算卸载(记为无压缩APSO)、蒙特卡洛法(记为MCMC)、全部MEC卸载执行策略(记为All MEC)以及全部本地卸载执行策略(记为All local)。这里,蒙特卡洛法是从可行解中随机选取1 000个样本,求最优值。

3.1 仿真环境及参数设置

K个用户随机分布在以基站为中心、半径为d的圆形覆盖区域内。信道建模综合考虑了大尺度及小尺度2种衰落特征。信道的大尺度衰耗表示为:

Loss(di)=A0+nlgdi,

(34)

式中:di为用户i到基站的距离,n为衰减指数,A0为固定常数。令Hw,i∈NT×NR,i代表上行链路中用户i与基站的小尺度衰落信道矩阵,其中Hw,i的元素是独立同分布的、均值为0,方差为1的复高斯随机变量。则上行链路的信道矩阵表示为:

(35)

同理,下行链路的信道矩阵可表示为:

(36)

根据用户数、卸载任务量和计算强度等指标进行仿真分析,仿真中主要用到的参数取值如表2所示。

表2 系统设置Tab.2 System configuration

3.2 结果分析

图3对APSO算法卸载策略的收敛性进行评估,其中迭代次数设置为100,粒子数N=200。考虑了用户设备数K为5和10这2种情况。可以看出,系统时延都随着迭代次数的增加而降低,2种情况下该算法均具有较好的收敛性。相比于10个用户,5个用户下的收敛速度更快、系统时延更低。

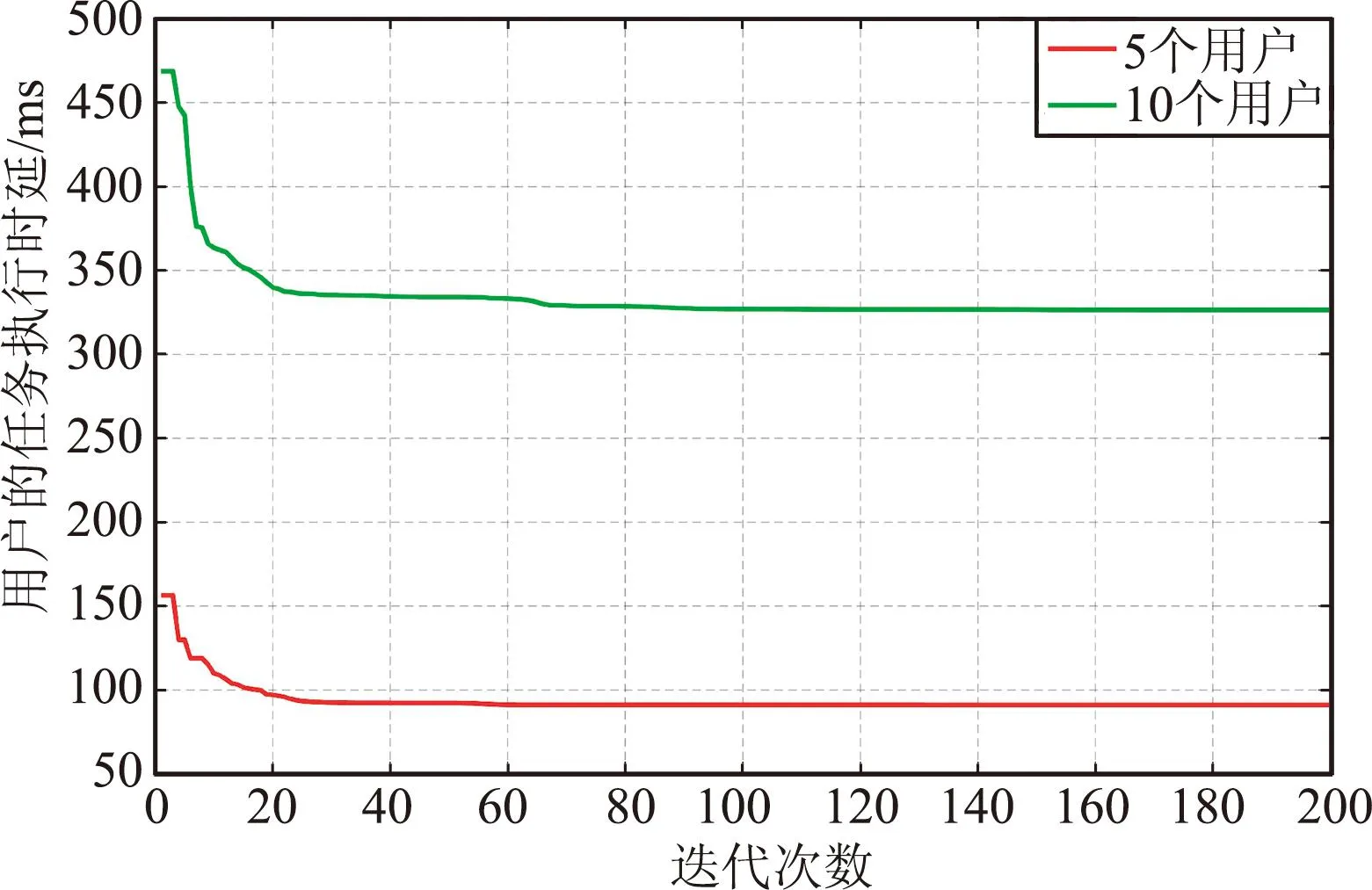
图3 收敛性分析Fig.3 Convergence analysis

图4展示了设备数对系统总时延的影响。可以发现,随着用户设备数的增多,任务处理能耗与时延也随之增加,系统的计算成本逐渐增加,5种卸载策略下的系统总时延均增长。当用户数K≤15时APSO、PSO、无压缩APSO和All MEC这4种方案下性能几乎重合;当用户数K>15时,APSO明显优于其他5种方案,但是APSO与PSO整体仅有微小差距。除此以外,当用户数K>30时,选择不压缩数据进行任务执行会耗费更多时间,原因是数据中存在一些多余成分即冗余度,通过对数据进行压缩处理,可以降低数据大小,从而在较短时间内传输数据。

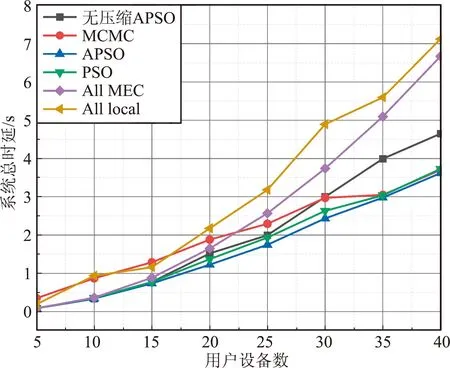
图4 系统总时延vs.设备数Fig.4 Total system delay vs. number of devices

图5展示了不同方案下任务计算强度对系统总时延的影响,其中设置UE数K=10,BS天线数及所有用户的天线数相等设置为4。由图可知,随着任务计算强度增大,PSO卸载方案、MEC卸载、无压缩APSO卸载方案、MCMC卸载方案与APSO卸载方案之间的系统时延差距逐渐拉大,全部本地卸载策略的系统时延远远高于其他策略,APSO算法的优化方案相比较于其他优化方案取得了较大的系统性能的提高。这说明,UE倾向于向MEC服务器卸载较多数据量(不是本地计算方式),从而降低任务执行时延。

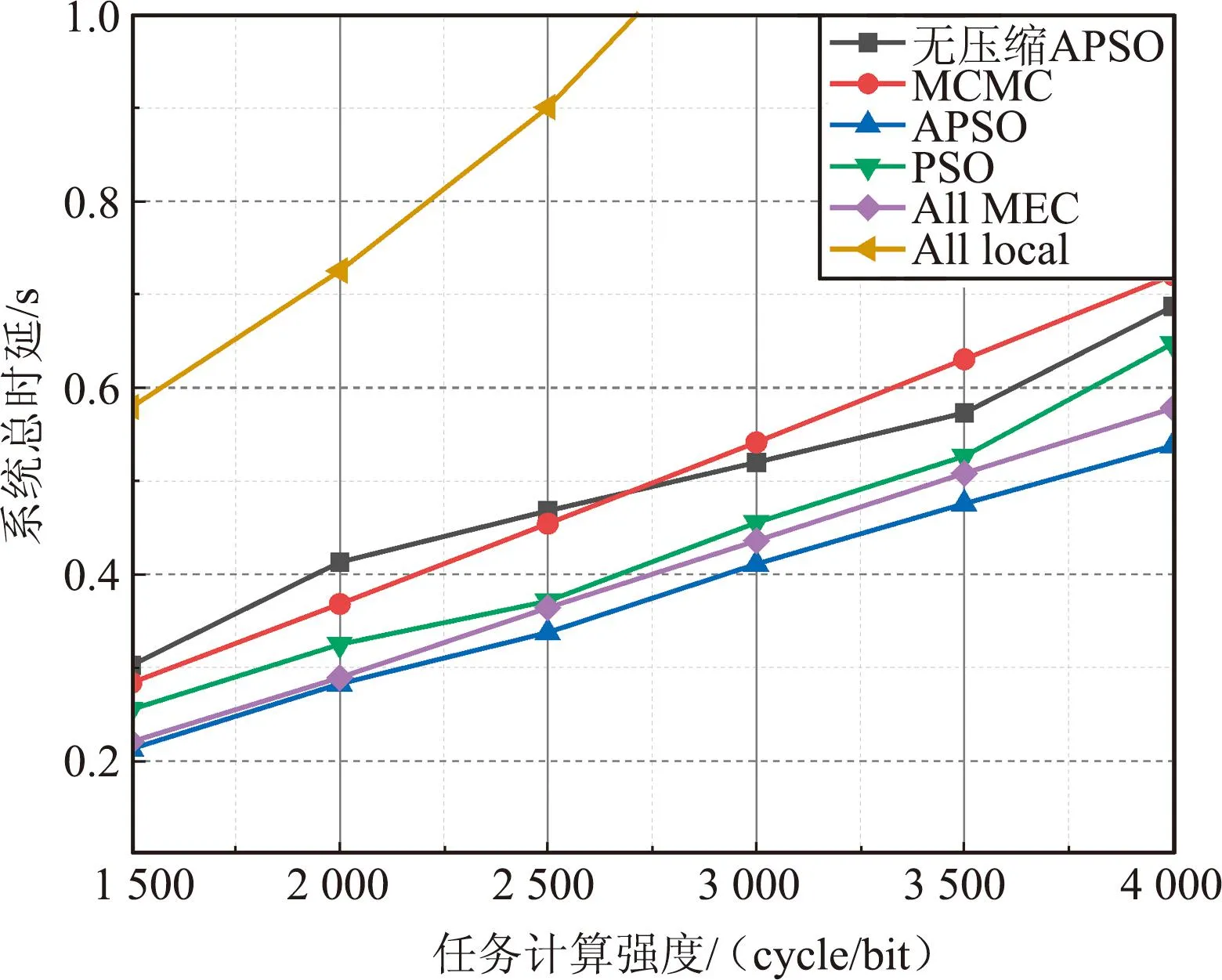
图5 系统总时延vs.任务计算强度Fig.5 Total system delay vs. task calculation intensity

图6描述了不同卸载方案下任务数据量大小与总时延的关系。随着任务数据的增加,无压缩APSO、APSO、PSO、All MEC、MCMC卸载方案与All local卸载策略的系统总时延均呈上升趋势,原因是任务计算量的增加会导致任务在计算过程中消耗更多的能量与时间,但APSO卸载方案产生的时延始终保持最小。在任务强度一定的情况下,PSO与APSO卸载方案效果接近,因此在考虑实践成本的投入时,可以优先考虑该方案,PSO策略也可做备选方案。

图6 系统总时延vs.任务数据量大小Fig.6 Total system delay vs. task data volume

4 结束语

针对具备数据压缩功能的多用户MIMO-MEC网络,研究了多用户任务卸载问题,通过联合优化任务卸载比例、数据压缩比例等参数来最小化系统总时延。在能耗、功率和带宽等约束条件下,将任务卸载归纳为非凸优化问题,并通过构造罚函数将其转化为一个相对简单的等价问题。为了求解该问题,基于APSO框架提出了多用户任务卸载方法。提出的方法根据粒子适应度自适应地调整权重,提高了寻优能力,得到了较好的局部最优解。通过仿真实验评估所提卸载方法的性能,分析用户数、任务计算强度等参数对系统性能的影响。结果表明,压缩因子的优化可以显著提升系统的性能;提出的方法优于本地计算、传统粒子群等对比方案,能够有效降低系统的任务执行时延。