基于智能反射表面的单站智能定位算法研究

谢文武，袁 婷，张海洋，李 敏，李桂林，李中年

(1.湖南理工学院 信息科学与工程学院，湖南 岳阳 414006；2.华中师范大学 物理科学与技术学院，湖北 武汉 430079)

0 引言

随着第五代移动通信技术大规模商用,全球业界已经开启对第六代移动通信技术(6G)的研究探索[1]。6G无线通信系统将有望集通信、智能、传感、定位和计算于一体[2-3],实现超可靠、节能的数据传输,以及人员和设备的精确定位,服务于物联网,实现“万物互联”的美好愿景[4-5]。智能反射表面(Reconfigurable Intelligent Surface,RIS)是6G潜在关键技术之一,被认为是一种全新的革命技术,可以通过编程的方式控制入射电磁波的传播,通过主动改变信道实现重新配置无线传播环境,由于其能提供无处不在的通信服务以及高灵活性受到了业界的广泛关注[6-8]。RIS可以创建虚拟视距(Line of Sight,LoS)来处理LoS被阻挡的问题,从而实现高精度定位。

传统定位法通过估计定位信号数据中与位置距离相关的参数,包括到达时间(Time Difference of Arrival,TDoA)[9]、到达角度(Angle of Arrival,AoA)[10]以及接收信号强度(Received Signal Strength,RSS)[11]等,再建立位置距离参数和用户位置之间的方程组并优化求解从而实现定位。传统两步定位法需要对原始信号进行处理,处理的过程中会产生一定范围内的误差,然后位置参数与位置之间的最终计算求解又会产生部分误差。因此传统两步定位法存在定位精度和分辨能力受限等问题。在以往研究过程中仿生智能优化算法在定位中广泛应用。文献[12]提出了一种基于模糊逻辑和极限学习机的无线传感网络定位混合模型,使用粒子群算法对该混合模型进行优化,使得估计的节点位置移动到更接近实际位置。仿真结果表明,该混合模型具有更高的定位精度,但是搜索速度慢、收敛过早等问题随之而来。

深度学习近些年得到了广泛的探索并取得了巨大的成功[13-14],特别是在计算机视觉方面。大量学者通过将深度学习技术应用到通信领域中[15],以解决通信中的一些难点问题,例如,无线定位[16]、信道估计[17]、无线接收机设计[18]等问题,深度学习作为未来在定位方面的研究热点之一,虽然已有学者开始将深度学习与RIS相结合,但主要的研究方向还是基于RIS辅助通信以及波束赋形等方面[19-20], 深度学习可提取信号核心特征,将其视为指纹储存于数据库。它高效处理原始数据,且随训练样本增加预测性能提升。参数化特性使其适用于实时定位,对训练数据量无明显限制。因此,研究基于深度学习的RIS辅助定位对未来实现高精度智能定位来说具有重要意义。

1 系统模型

RIS辅助定位场景如图1所示。

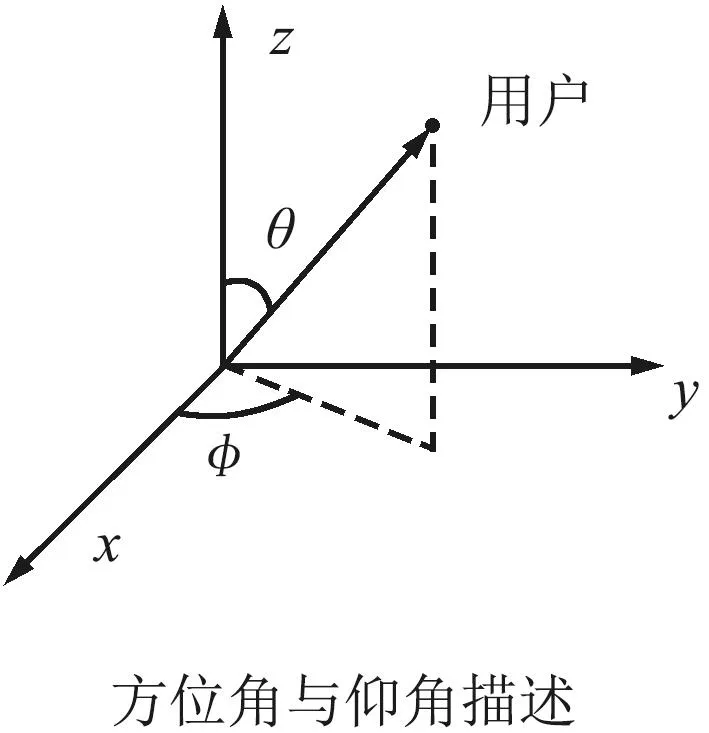
(b)矢量的方位角与仰角

考虑一个三维立体场景,该场景包括一个多天线基站、一个单天线用户以及一个RIS,RIS为包含NR个反射单元的均匀平面阵列(Uniform Planar Array,UPA),基站为配备了NB根天线的ULA,用户接收来自基站发送的信号和RIS反射的信号。BS的位置表示为p=[px,py,pz]T,用户的位置表示为q= [qx,qy,qz]T,RIS的位置为r=[rx,ry,rz]T,其中基站与RIS位于同一水平面,用户位于RIS与基站的下方。

假设UE可以直接接收BS发射的信号和通过RIS反射的信号,UE的下行链路信号模型可以表示为:

(1)

式中:hBU、hBR、hRU分别为BS-UE、BS-RIS、RIS-UE之间的信道,n是均值为0、方差为σ2的加性高斯白噪声,Ω=diag(ejω)=diag(ejω1,ejω2,…,ejωN)是RIS的相移矩阵,diag(·)表示对角矩阵。

根据对角矩阵性质:

(2)

根据式(2),基站与用户之间的等效信道可以表示为:

(3)

BS和RIS之间的信道表示为:

(4)

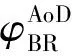
(5)

式中:N1、N2分别表示RIS的水平和垂直反射单元数量,dR表示RIS反射单元之间的间距,λ表示波长,⊗表示克罗内克积。aBS(φAoD)表示BS的阵列响应。由于BS的阵列天线为ULA,BS的阵列响应表示为:

(6)

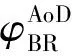
RIS与UE之间的信道hRU表示为:

(7)

式中:ρRU表示RIS与UE之间信道复增益,τRU表示RIS与UE之间的延迟,φRU、θRU分别表示RIS与UE之间AoD的方位角和仰角,aRIS(φRU,θRU)表示RIS的导向矢量。

(8)

BS和UE之间的信道表示为:

(9)

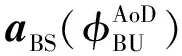
BS、RIS以及用户之间的几何关系如下:

(10)

(11)

(12)

(13)

(14)

2 基于深度学习的指纹定位

指纹定位技术由于成本低、受环境影响小和复杂度低等优点逐渐成为无线定位技术的热点。其本质是建立位置与信号数据之间的映射,这种映射在一定程度上是非线性的,而深度学习恰好擅长建立数据之间的非线性映射。因此,考虑将深度学习应用到指纹定位中。指纹定位中,与传统基于RSS的指纹定位相比,基于信道状态信息(Channel State Information,CSI)的指纹识别具有更细粒度的信息。基于深度学习的指纹定位系统如图2所示,总结了基于深度学习的指纹定位的工作流程,主要分为指纹填充阶段(即训练阶段或离线阶段)和指纹匹配阶段(即在线阶段)两个阶段。

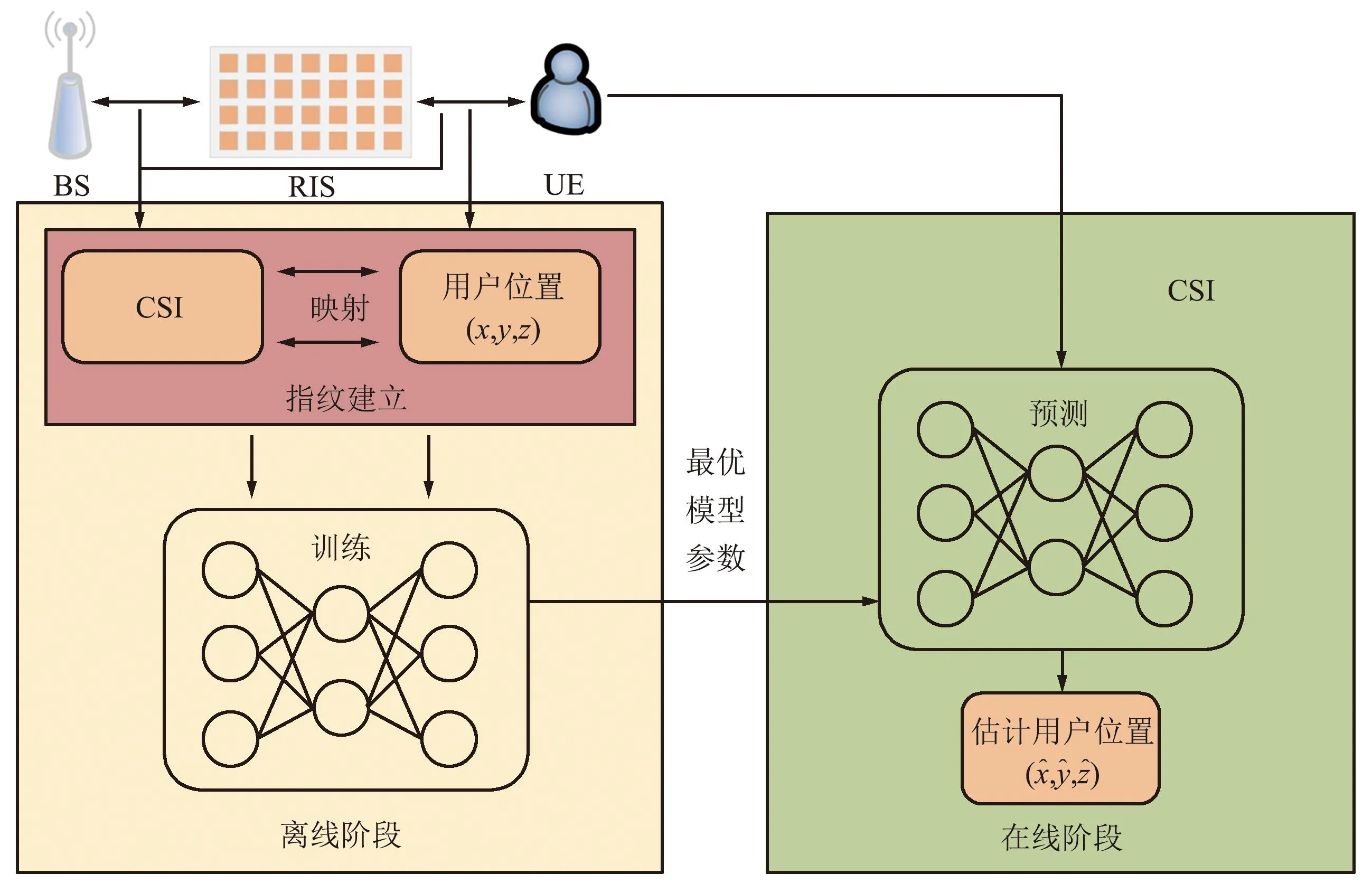
图2 基于深度学习的RIS辅助定位给离线和在线阶段Fig.2 RIS assisted positioning for both offline and online stages based on deep learning

离线阶段,创建指纹数据库,其中包括各个用户位置的坐标信息以及CSI。假设K个用户坐标,每个坐标为q=[xk,yk,zk]T,其中k=1,2,…,K以及其对应的CSI记为CSIk。指纹数据库创建后,用户训练神经网络模型,旨在揭示CSI和用户位置之间的关系。在提出基于深度学习方法的在线阶段,将CSI传递给设计神经网络模型,神经网络模型输出该用户位置的坐标。

指纹的生成,基于CSI的指纹通常具有如下形式:

Fi(x,y,z)=[CSI1,CSI2,…,CSIN],

(15)

式中:Fi(x,y,z)表示具有地理坐标(x,y,z)的用户在第i处位置生成的指纹,CSIn表示第i处位置从第n个基站接收到的CSI,而在基站多天线的情况下,也可以表示从第n根天线接收CSI;N表示天线或基站的数量。

指纹匹配技术通常使用基于欧式距离的匹配法来实现,该算法包括测量记录的指纹与数据库中每个参考位置之间的欧式距离,2个指纹之间的欧式距离定义为:

(16)

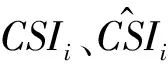
3 基于深度学习的RIS辅助定位

3.1 指纹库的设计

为了创建指纹库,对用户的K个位置中的每个位置进行了估计,通过收集所有用户位置的估计值,创建所有用户对应的指纹库信息集合T:

T≜{(q1,H1),(q2,H2),…,(qK,HK)},

(17)

式中:qk≜[qk,x,qk,y,qk,z]表示用户的第k个位置,k=1,2,3,…,K;Hk表示用户位于对应位置qk时基站与用户之间的等效信道。

3.2 神经网络模型

Transformer网络模型于2017年被提出,一经出现就受到了业界的广泛关注。Transformer网络模型不用重复和卷积,文献[21]通过实验证明了该网络模型在质量上更优,同时更易于并行化,且所需的训练时间明显更少。Transformer架构特别擅长处理序列数据,对序列数据中的长距离依赖进行建模。无线定位数据类似于序列数据,所以本文采用基于注意力机制的Transformer网络模型,优化了解码器的性能,使网络性能达到最优。

定位神经网络模型的主干网络由2个Transformer的编码器组成,将通过线性层进行位置映射。其中Transformer的编码器结构主要分为 2个子层:一层为MHA;另一层为前馈神经网络。在2个子层的每个周围使用残差连接,然后进行层归一化,即归一化层。经过归一化之后每个子层的输入就是LN(x+M(x)),LN表示层归一化(Layer Normalization)操作,M表示多头注意力机制。通过训练定位神经网络模型将CSI与位置形成映射,然后使用L1损失函数来计算估计位置与真实位置的误差损失值。

通过对查询序列和键序列的相关性建模计算权重系数,从而根据权重系数对值进行加权求和,就是输入向量生成3个向量。在实际应用,将查询、键和值分别打包成矩阵Q、K、V,注意机制表示为:

(18)

式中:A(·)表示注意力机制集成,softmax表示将一个实数向量转换为一个概率分布的函数,dk表示Q和K的维度,QKT的值越大表示Q和K的相似度越高。

MHA本质上是多个独立的注意机制集成,允许模型在不同位置共同关注来自不同子空间的信息,然后由多个独立的注意力层并行处理,具有强大的表达能力。MHA的计算MHead可以表示为:

(19)

(20)

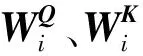
前馈神经网络由2个线性层组成,其激活函数为ReLU函数:

FFN(x)=ReLU(xW1+b1)W2+b2,

(21)

式中:x为上一层的输出,W1、W2、b1、b2均为可训练参数。

3.3 算法流程

整个Transformer网络模型的输入为BS与UE之间的等效信道信息,包括LoS链路和非视距(Non-Line of Sight,NLoS)链路,输出则是用户的位置,其算法实现流程如算法1所示。

算法1 基于深度学习的定位算法初始化:训练数据(H,q),测试数据(Htest,qtest),最大训练周期Epoch。离线训练阶段: for i in range(Epoch): 随机初始化网络参数;

通过算法1可知,网络通过输入处理好的CSI,经过设计好的神经网络进行位置估计,输出结果可以表示为:

(22)

式中:f(·)表示CSI与位置之间映射的神经网络算法。

网络采用均方根误差(Root Mean Square Error,RMSE)作为损失函数来训练网络模型参数。RMSE是一种用于衡量预测值与实际值之间差异的统计量,它表示了预测值与实际值之间的平均误差的平方根,计算如下:

(23)

4 仿真结果

仿真实验采用Matlab作为通信链路仿真平台,PyTorch作为深度学习开发平台。假设系统位于一个20 m×20 m×5 m的空间直角坐标系中,BS和RIS的位置分别为p=[0,0,5]T、r=[12,7,5]T,BS与RIS位于同一高度,用户位于BS下方5 m处的平面上。模拟不同的目标用户,用户按照0.5 m的分布在此空间范围内建立离线训练所需的指纹库数据。RIS反射单元数为NR=36,基站天线数为NB=16。信道增益振幅根据自由空间公共路径损耗模型生成,载波频率为fc=60 GHz。

4.1 仅存在视距链路结果分析

本节考虑只存在LoS链路的定位场景,未引入RIS的情况下使用Matlab生成基站与用户之间的信道矩阵HLoS和对应的用户位置信息,BS为配备了NB=16根天线的ULA,将信道矩阵HLoS以及用户位置信息送入Transformer网络模型进行训练,实验结果如图3所示。

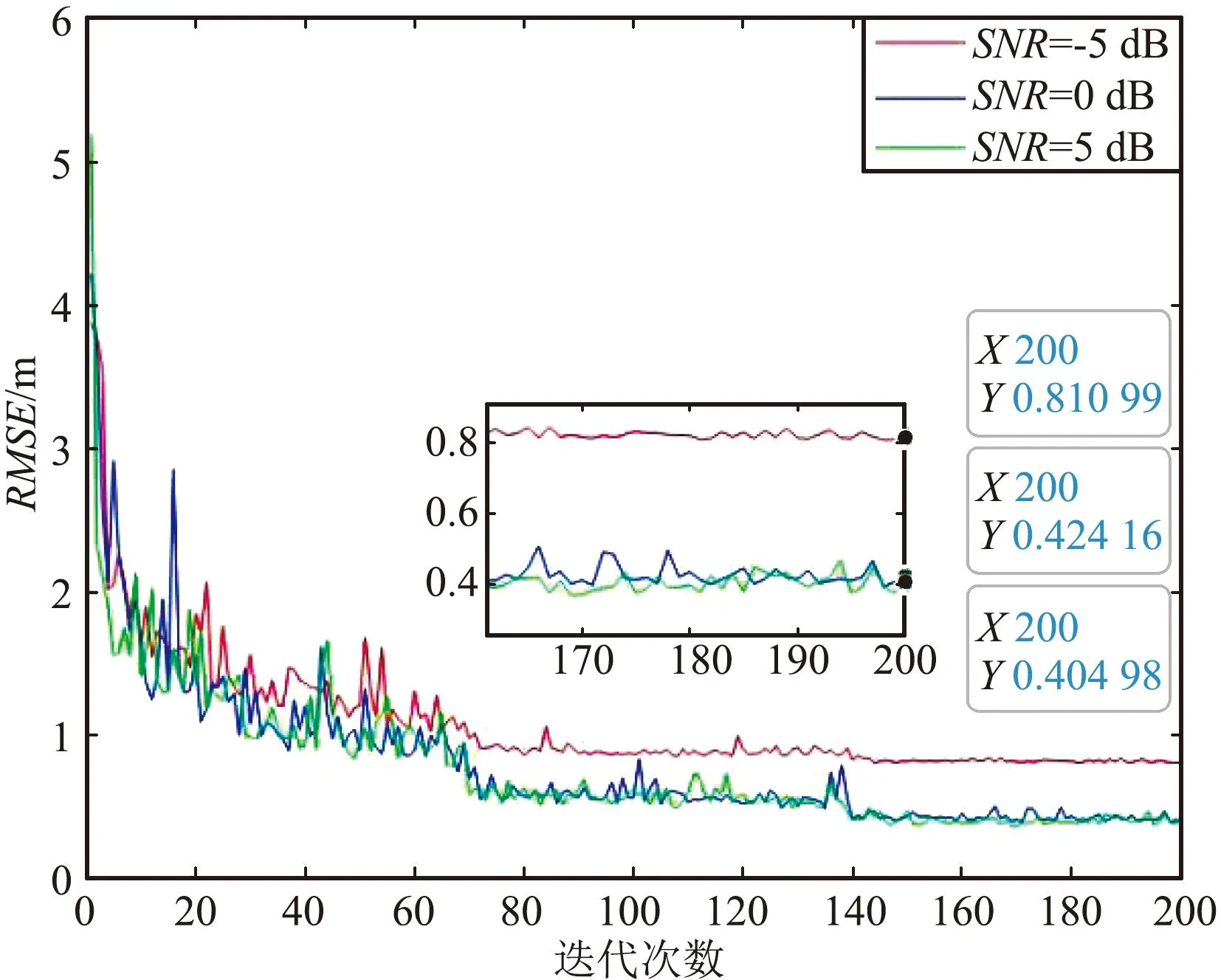
图3 仅存在LoS链路时的RMSE Fig.3 RMSE for only LoS link presence

从图3可以看出,刚开始进行训练时,RMSE的值较大,但随着迭代次数的增加,RMSE开始收敛,并趋于平稳状态,说明CSI与用户位置之间的确存在一定的映射关系,可以通过CSI实现无线定位。当RMSE收敛时,可以看出随着信噪比(Signal to Noise Ratio,SNR)的增加,RMSE逐渐下降,说明定位精度逐渐上升。

4.2 仅存在反射链路结果分析

考虑只存在NLoS链路的定位场景下的仿真分析,即LoS链路被障碍物阻挡,使用Matlab生成仅存在NLoS链路下的信道矩阵HNLoS,BS为配备了NB=16根天线的ULA,RIS为配备了NR=36个反射单元的UPA,将信道矩阵HNLoS和对应的用户位置信息输入神经网络进行训练,实验结果如图4所示。

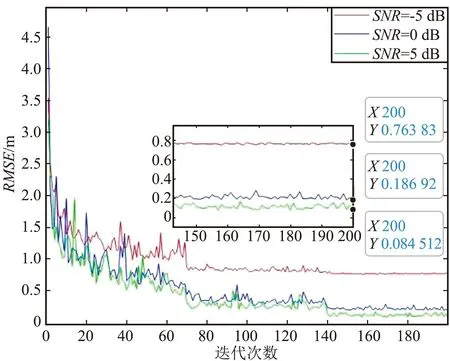
图4 仅存在反射链路的RMSE Fig.4 RMSE for only reflective link presence

由图4可知,当SNR不变时,随着迭代次数的增加,RMSE开始逐渐收敛稳定,说明RIS辅助定位场景下CSI与位置之间也存在一定的映射关系,RIS辅助定位场景下也能通过CSI实现无线定位。随着SNR的增加,RMSE最终收敛的数值逐渐下降,说明定位精度逐渐上升。

由图3与图4对比分析可知,在SNR=-5、0、5 dB时,仅存在LoS链路的稳定后的RMSE劣于仅存在反射链路。在SNR=0、5 dB时,仅存在LoS链路时 2种条件下的RMSE分别为0.404 98 m和0.424 16 m,在仅存在反射链路中引入RIS辅助定位后定位精度提升比较明显,RMSE的值达到0.186 92 m和 0.084 512 m。尽管在高SNR条件下,理论上仅存在LoS链路是最佳的信号路径,但实验表明引入RIS辅助定位后,仍可以提高定位精度。在低SNR条件下,经RIS优化的反射链路可能会表现得更好,RIS提供了一种机制,可以“聚焦”或增强信号优化信号的传播环境,改善在低SNR条件下受损的信号质量,提供更多的位置信息,通过Transformer网络建立CSI与位置之间较好的关系映射,从而实现更高精度的定位。

4.3 LoS链路和反射链路共存结果分析

考虑LoS链路与NLoS链路共存的定位场景下的仿真分析,使用Matlab生成LoS链路与NLoS链路共存下的信道矩阵H,基站为配备了NB=16根天线的ULA,RIS为配备了NR=36个反射单元的UPA,将信道矩阵和对应的用户位置信息输入神经网络进行训练,实验结果如图5所示。

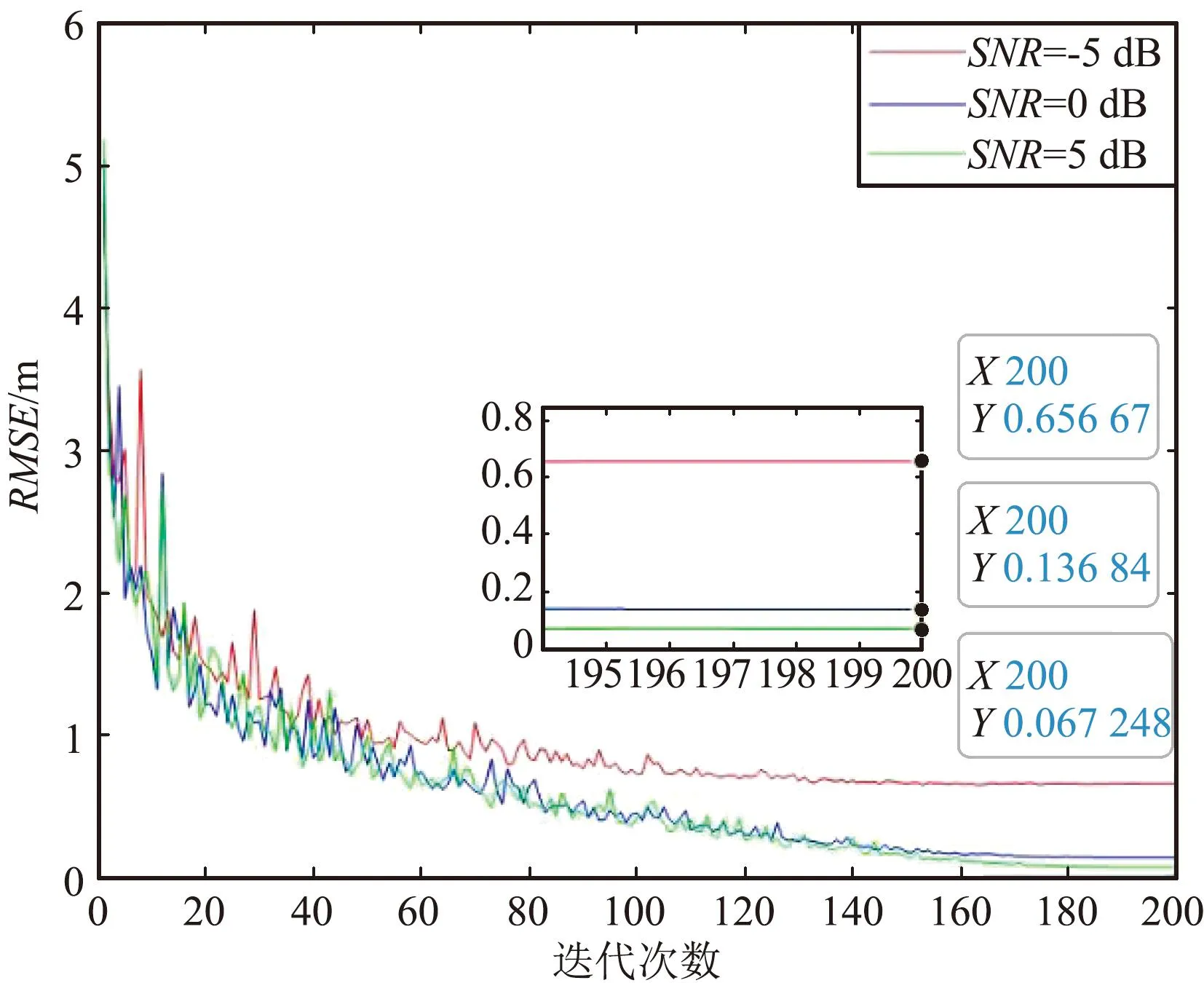
图5 LoS链路和反射链路共存时的RMSE Fig.5 RMSE for both LoS link and reflective link presence

由图5可以看出,随着迭代次数的增加,RMSE开始逐渐下降收敛,随着SNR的增加,RMSE也逐渐下降。当SNR=-5 dB时,RMSE最终可以收敛到 60 cm左右,当SNR=5 dB,RMSE最终可以收敛到 6 cm左右。与图3和图4对比分析可知,LoS链路和反射链路共存的定位场景下,RMSE最终收敛的数值更低,说明2条链路都存在的情况下能实现更高精度的定位。当引入RIS辅助定位时,LoS链路存在的情况下能与RIS共同提供更多的位置信息,通过Transformer网络建立CSI与位置之间的更准确的映射关系,从而实现更精度的定位。

当SNR=-5 dB时,图6展示了不同反射单元数量与RMSE之间的曲线。由图6可知,当SNR不变时,随着RIS反射单元数量的增加,RMSE在逐渐下降,说明定位精度随着RIS反射单元的增加而增加。当RIS反射单元增加时,RMSE也能快速收敛并稳定,说明基于深度学习的RIS辅助定位场景下,也可以通过增加RIS反射单元数量来提高定位精度,且该网络模型再训练过程中也能快速收敛。

图6 SNR=-5 dB RIS反射单元数量的RMSE Fig.6 SNR=-5 dB RIS RMSE for the number of reflective elements

当SNR=0 dB时,图7展示了不同反射单元数量与RMSE之间的曲线。可以看出,当SNR一定的情况下,随着RIS反射单元数量的增加,RMSE在逐渐下降,说明定位精度随着RIS反射单元的增加而增加,与图6的趋势一致。与图6对比分析可知,在不同SNR情况下,RMSE都随着RIS反射单元数量的增加而降低,且不论RIS反射单元数量的多少,RMSE都会随着SNR的增加而下降。

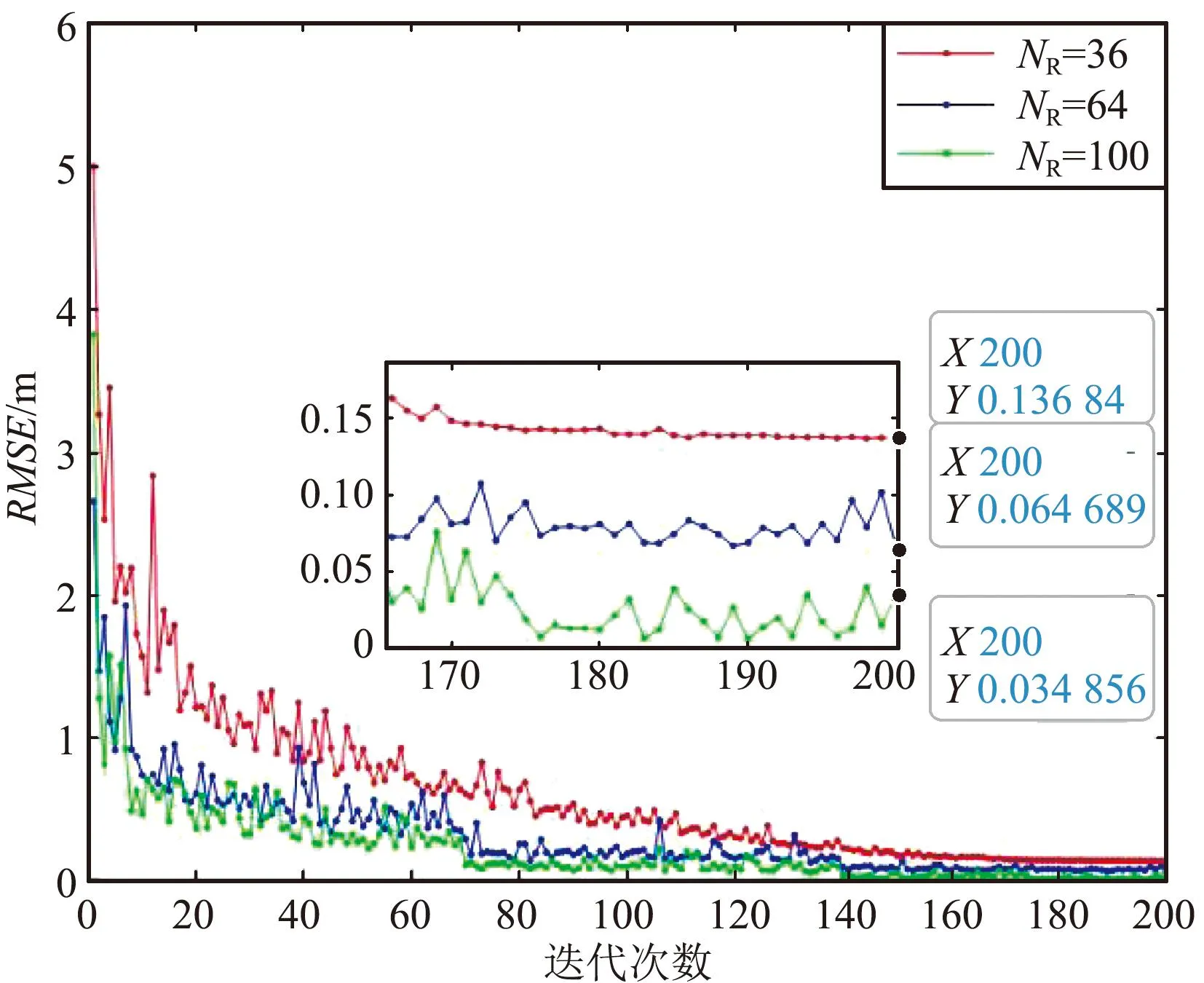
图7 SNR=0 dB RIS反射单元数量的RMSE Fig.7 SNR=0 dB RIS RMSE for the number of reflective elements

4.4 算法对比结果分析

本节展示了LoS链路和反射链路共存情况下,不同定位方法在SNR=-5、0、5 dB下位置预测误差,BS为配备了NB=20根天线的ULA,RIS为配备了NR=36个反射单元的UPA,分别对比布谷鸟搜索算法(Cuckoo Search Algorithm,CS)、RIS辅助定位系统中位置的最大似然(Maximum Likelihood,ML)函数定位算法。

表1展示了对比RMSE结果,随着SNR的增加定位精度均提高。本文提出的算法在SNR=-5 dB时优于ML算法,次于CS算法,在SNR=0、5 dB时均优于对比的算法。CS是Yang等提出的一种启发算法,通过模拟布谷鸟的寄生育雏来有效寻找问题的最优解。它对噪声具有一定的鲁棒性,因为它们在搜索过程中不仅仅依赖于当前的测量数据,还结合了其他可能的解,并且通过其更新策略动态地适应搜索空间,使其能够在不断变化的环境中(如低SNR条件下的噪声变化)进行有效搜索,因此它在低SNR环境中能够实现较高的定位精度,但在SNR=0、5 dB时CS算法的地位精度劣于本文算法,由此可以得出,提出的算法对高SNR情况下定位更加友好。

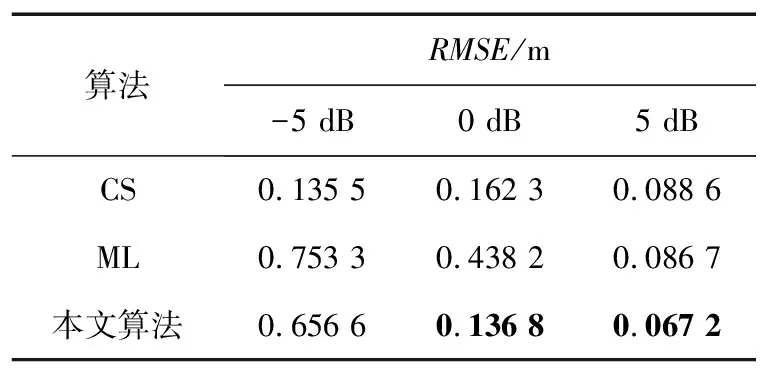
表1 算法对比RMSE值

5 结束语

本文主要研究了RIS辅助的多输入单输出无线定位系统,针对RIS辅助三维定位场景,通过利用BS与UE之间等效信道与位置之间的关系,将CSI与位置信息作为指纹信息,提出了一种基于深度学习的RIS辅助定位算法模型。主干网络采用Transformer作为网络结构,基于深度学习的指纹定位通过离线训练输出最优网络参数,然后通过在线阶段实现高精度定位。实验表明,基于Transformer模型的定位系统在仅存在LoS链路、仅存在NLoS链路以及LoS链路和NLoS链路都存在的定位场景下均表现出色,具有良好的鲁棒性。深度学习的RIS辅助定位系统在实验中取得了显著的成果,尤其在RIS辅助场景下的定位精度明显优于其他情况。此外,实验证实了RIS反射单元数量对定位精度的重要影响,随着数量增加,定位精度随之提升。