基于张量的RIS辅助波束空间MIMO系统信道估计
2024-03-05郭歆莹解宗元
郭歆莹,解宗元
(1.河南工业大学 粮食信息处理与控制教育部重点实验室,河南 郑州 450001;2.河南工业大学 河南省粮食光电探测与控制重点实验室,河南 郑州 450001;3.河南工业大学 信息科学与工程学院,河南 郑州 450001)
0 引言
传统的多输入多输出(Multiple Input Multiple Output,MIMO)技术为每根天线配置专用射频(Radio Frequency,RF)链路,导致毫米波(millimeter Wave,mmWave)MIMO系统硬件成本高和能量消耗大[1-2]。为了减少RF链路数量,Sayeed等[3]提出了基于透镜天线阵列的波束空间 MIMO技术。
透镜天线阵列由一个电磁透镜和放置在其焦面上的天线组成,可以将不同方向(波束)的信号汇聚到不同的天线上,实现传统空间信道与波束空间信道之间的转换。由于波束空间信道的稀疏特性,选择少量主导波束即可减少RF链路数量和系统维度,构成低复杂度和低成本的系统。波束空间MIMO系统中的波束选择[4]、信道估计[5]等技术成为当前通信领域的研究热点。
透镜天线阵列能够降低mmWave MIMO通信系统的成本和复杂度,但不能解决mmWave信号易被障碍物遮挡的问题。近年,随着数字超材料的发展,可重构智能表面(Reconfigurable Intelligent Surface,RIS)作为解决覆盖盲区问题的一种突破性技术应运而生。它可以扩展信号覆盖范围、克服传输距离限制、解决mmWave频段传输信号阻塞的难题。具体来说,RIS是一种由大量低成本的被动无源反射单元组成的平面,具有独特的物理结构且各反射单元独立可控。通过对反射单元的联合调控,可以达到调整入射信号相位、幅度等参数的目的,并能有利地改变发射端与接收端之间的无线信道。因此,RIS成为未来通信领域的一个极具潜力的研究方向[6-7]。
由RIS辅助的通信系统吸引了广大学者的关注,尤其是在信道估计领域。Hu等[8]提出了双时间尺度信道估计框架和双链路引导传输方案,显著地降低了导频训练开销。Wang等[9]利用mmWave信道固有的稀疏特性以及Katri-Rao积和Kronecker积的性质,挖掘了级联信道的稀疏表示,将级联信道估计问题转化为稀疏信号恢复问题,并采用正交匹配追踪算法对稀疏信号进行恢复,以较低的训练开销获取了相应的级联信道。
除上述方法外,还有一些学者利用张量解决RIS辅助通信系统的信道估计问题。张量作为一种有效的数学工具,在各种信号处理问题中有着广泛应用[10-11]。张量分解可以将一个高维张量分解为多个秩一矩阵的线性组合,由于低秩矩阵估计的低复杂度,张量分解被认为是估计MIMO通信系统中多个大信道矩阵的有效方法。De Araújo等[12]利用张量建模方法将接收信号构造成三阶张量,并基于并行因子(Parallel Factor,PARAFAC)分解提出了 2种有效的信道估计方法:第一种基于级联MIMO信道的Khatri-Rao分解求解Rank-1矩阵逼近问题从而得到闭式解;第二种利用了迭代双线性交替最小二乘(Alternative Least Squares,ALS)算法。Wei等[13]研究了RIS辅助的多用户多输入单输出通信系统的上行信道估计,提出了一种基于PARAFAC分解的信道估计框架,并采用2种迭代算法来估计基站(Base Station,BS)和RIS之间的信道以及RIS与用户之间的信道。Zheng等[14]研究了RIS辅助mmWave正交频分复用系统的下行链路信道估计问题,通过探索mmWave信道固有的稀疏散射特性,将接收信号表示为一个低秩三阶张量,利用极少量的导频开销就能获得可靠的级联信道估计。Zhang等[15]提出了一种基于稀疏结构化张量分解的信道估计算法,同时利用压缩感知和张量分解技术有效降低了训练开销。以上关于张量分解在信道估计领域的研究工作通过对不同系统建立相应的张量模型,进而利用张量分解有效估计信道状态信息。由于不同系统蕴含的多维特征信息不同,其张量模型的构建思路和张量分解的内在机理也不尽相同。
与上述研究不同,本文探究了BS采用透镜天线阵列的RIS辅助波束空间MIMO系统。该系统结合RIS和透镜天线阵列的优点,不仅能够扩展信号覆盖范围、提高接收信号质量,而且可以减少RF链路数量,因此该系统具有低成本、低能耗和低复杂度的特点[16-17]。然而,在此系统中进行信道估计是一项极具挑战性的任务,因为波束空间信道的维度较大,而BS的RF链路数量有限;RIS中无源反射单元数量较多且缺乏信号处理能力。针对以上难题,本文提出一种基于张量的迭代信道估计算法。该算法构建了BS接收导频信号的三阶张量模型,利用PARAFAC特定代数结构获得了良好的信道估计性能。本文首创利用张量方法求解RIS辅助波束空间MIMO通信系统信道估计。本文的主要贡献可总结为以下3点:① 在导频传输过程中,BS将接收到的导频信号建模为三阶张量,建立波束空间MIMO系统的信道估计问题;② 采用PARAFAC分解和ALS算法进行信道估计;③ 分析了PARAFAC分解的唯一性条件,该条件能够为系统参数选择提供理论指导。
1 系统模型
1.1 RIS辅助波束空间MIMO系统
RIS辅助波束空间MIMO系统,如图1所示。BS采用具有K根透镜天线的均匀线性阵列并配备KRF个射频链路, RIS为由N个能够单独调节其反射系数的反射单元构成的平面。该系统工作在时分双工模式,并且在同一时频资源块上支持M个单天线用户。由于mmWave链路极易受到环境阻塞的影响,本文假设BS与用户之间的直接链路被阻塞。
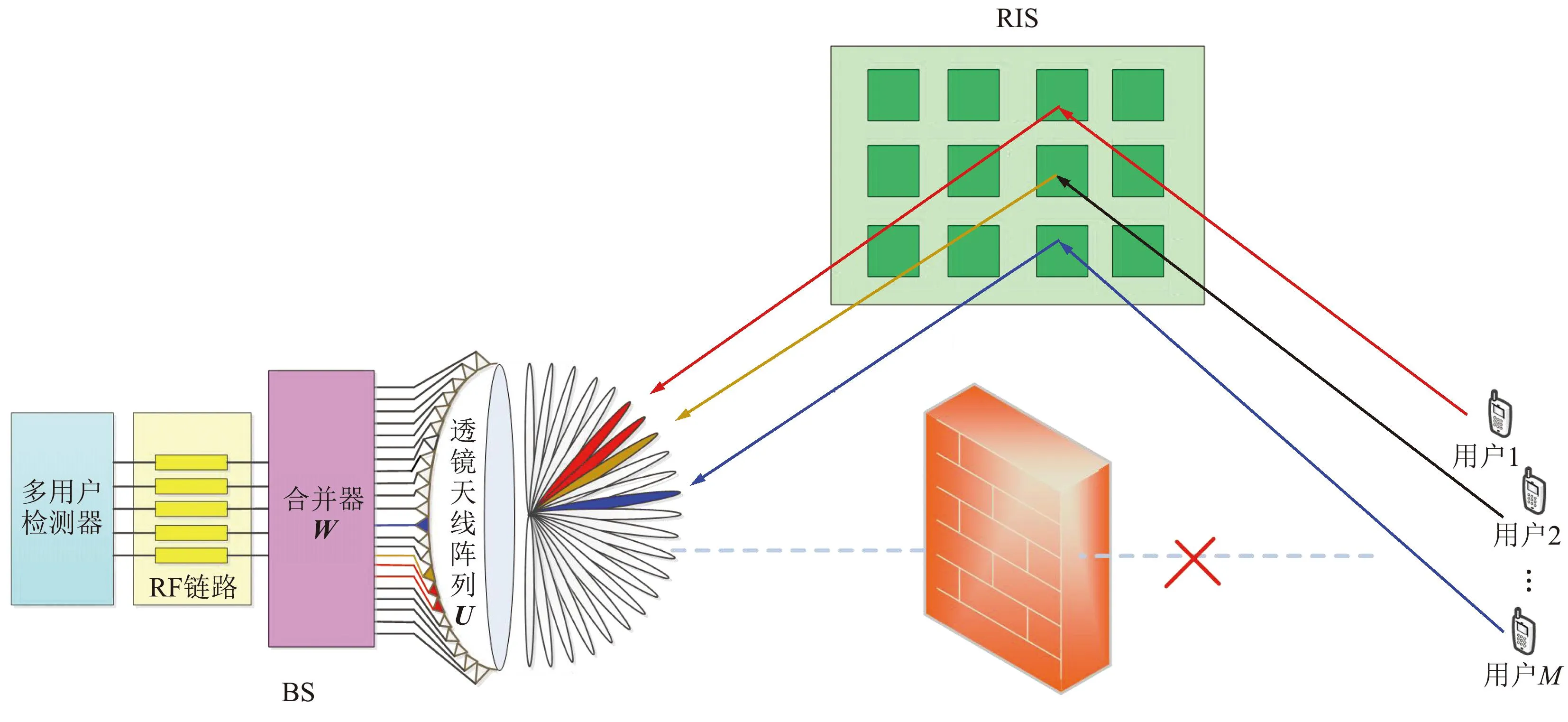
图1 RIS辅助波束空间MIMO系统Fig.1 RIS-assisted beam-space MIMO systems
令G∈K×N表示RIS与BS之间的信道,H=[h1,h2,…,hM]∈N×M表示M个用户与RIS之间的信道,hm∈N×1表示第m个用户到RIS的信道,其中m=1,2,…,M。
mmWave MIMO系统一般采用Saleh-Valenzuela信道模型[18],该模型下的信道矩阵G可表示为:
(1)
(2)
(3)
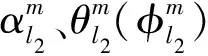
为了减少射频链路数量,即KRF≪K,本文在BS端采用透镜天线阵列。透镜天线阵列起到空间离散傅立叶变换(Discrete Fourier Transform,DFT)矩阵U∈K×K的作用,将传统的无线信道转换为波束空间信道。覆盖整个角度空间的K个正交波束的阵列导向矢量为:
(4)

Yp=UGDp(Φ)HX+Zp,
(5)
式中:Dp(Φ)∈N×N表示由RIS相移矩阵Φ∈P×N的第p行构成的主对角线上元素的对角矩阵,X∈M×T包含T个时隙内的发射信号,为了保证信道估计的效率,T必须大于等于M;Zp∈K×T表示复加性白高斯噪声(Additive White Gaussian Noise,AWGN)矩阵,其元素每个维度均值为0、方差为σ2/2。
1.2 张量信号建模
假设式(5)中采用正交导频信号,即XXH=IM。在导频传输过程中,BS利用第q个合并器Wq∈KRF×K对接收到的上行信号矩阵Yp进行合并,则由KRF个射频链路采样得到的基带信号Yp,q∈KRF×T为:
Yp,q=WqUGDp(Φ)HX+WqZp,
(6)
式中:q=1,2,…,Q,Q=K/KRF。BS接收到的上行信号经过Q个合并器处理后,得到Q个矩阵Yp,q(1≤q≤Q),将Q个矩阵在列方向上堆叠得到:
WUGDp(Φ)HX+WZp。
(7)
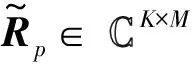
(8)

(9)
式中:F=WUG∈K×N。依据PARAFAC分解,矩阵Rp=FDp(Φ)H∈K×M可以看作是一个秩为N的三阶张量∈K×M×P的第p个前向矩阵切片。当k=1,2,…,K,m=1,2,…,M时,Rp的每个元素可以表示为:
(10)

(11)
(12)
(13)
式中:⊙表示Khatri-Rao积。
2 基于PARAFAC分解的信道估计方法
2.1 ALS信道估计
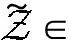
(14)

(15)
(16)
(17)


算法步骤输入:Φ,δ=10-5,Imax;初始化:i=0,^G(0),^F(0); do i=i+1 通过^H(i)=(Φ☉^F(i-1))†R2 计算^H(i); 通过^F(i)=((^HT(i)☉Φ)†R1)T更新^F(i); 通过^G(i)=(WU)†^F(i)更新^G(i); Until i>Imax或者收敛条件式(22)得到满足;输出:估计出的G和H。
具体步骤如下。
② 迭代更新:基于以下2个代价函数,通过固定H交替优化F,固定F交替优化H:
(18)
(19)
则G和H的信道估计闭式解分别为:
(20)
(21)
③ 迭代终止准则:当达到最大迭代次数Imax或者当
(22)
即达到收敛条件,所提的ALS算法终止。其中δ是一个小的正阈值,例如δ=10-5。
2.2 唯一性条件
为了保证所提算法的可行性,讨论PARAFAC分解的唯一性条件[19]。本文将Kruskal的唯一性条件用于PARAFAC模型,以获得系统设计理论指导。令kA表示矩阵A的Kruskal秩(k秩),利用PARAFAC模型的唯一性定理,可以证明若:
kF+kH+kΦ≥2N+2,
(23)

不等式(23)建立了(F,H,Φ)唯一性的充分条件。根据所考虑的信道模型,每个用户与RIS之间各条路径的方位角和仰角通常不同,因此H满k秩。由于Φ是DFT矩阵,因此Φ也为满k秩。根据式(9),W和U都是满k秩,所以F的秩等于G的秩。G秩亏,并且G的k秩等于RIS和BS之间的路径数LG。因此,在这种情况下,式(23)可以改写为:
min{LG,N}+min{N,M}+min{P,N}≥2N+2。
(24)
通常情况下,实际部署中的RIS元素数目N较大,大于RIS与BS之间的路径数目LG或移动用户数目M,而且P≤N。因此,本文提出模型的PARAFAC分解唯一性条件并不容易满足。
为了解决此问题,本文将具有N个元素的RIS划分为互不重叠的子块。例如,当N=128,P=N,LG=5,M=16时,N≫max{LG,M},这显然不满足 式(24)。然而,可以通过将RIS拆分为8个互不重叠的子RIS,使得每个子RIS仅包含16个元素来满足式(24)。所提出的ALS算法可以用于估计与 8个子RIS相关的信道,将与8个子RIS相关的信道估计级联即可得到整个128元素RIS的期望信道估计。
3 仿真结果与分析
信道估计精度通过归一化均方误差(Normalized Mean Square Error,NMSE)来衡量:
(25)
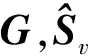
由于目前还没有任何一种方案对RIS辅助波束空间MIMO系统的信道G和H进行估计,因此本文仅将提出方案与理想化最小二乘(Least Squares,LS)方案进行比较。理想化LS方案为:在给定用户和RIS之间完美信道矩阵H的情况下,计算RIS和BS之间信道矩阵G的LS估计值,并在给定完美G的情况下计算H的LS估计值。假设K=32,M=N=T=P=16,LG=5。所提ALS算法与理想化LS算法的NMSE性能比较如图2所示。从图2可以看出,本文所提算法对H的估计精度与理想化LS算法基本相同,因为随着信噪比(Signal to Noise Ratio,SNR)的增大,2条NMSE曲线基本重合;另一方面,所提算法得到的G估计性能与理想化LS估计性能之间仅存在约2 dB的NMSE差距。这表明,本文所提ALS算法达到了较好的估计精度。
假设M=N=T=P=16,LG=5。图3给出了BS天线数K∈{16,64}时,所提ALS信道估计算法的NMSE性能随SNR的变化情况。图3结果表明,随着K值增加,信道估计的NMSE性能越好,这是因为导频训练序列长度与K值成正比。另外,随着K值增加,信道G的NMSE性能并没有信道H改善明显,这是因为K值越大,G维数越大,但H维数不变。
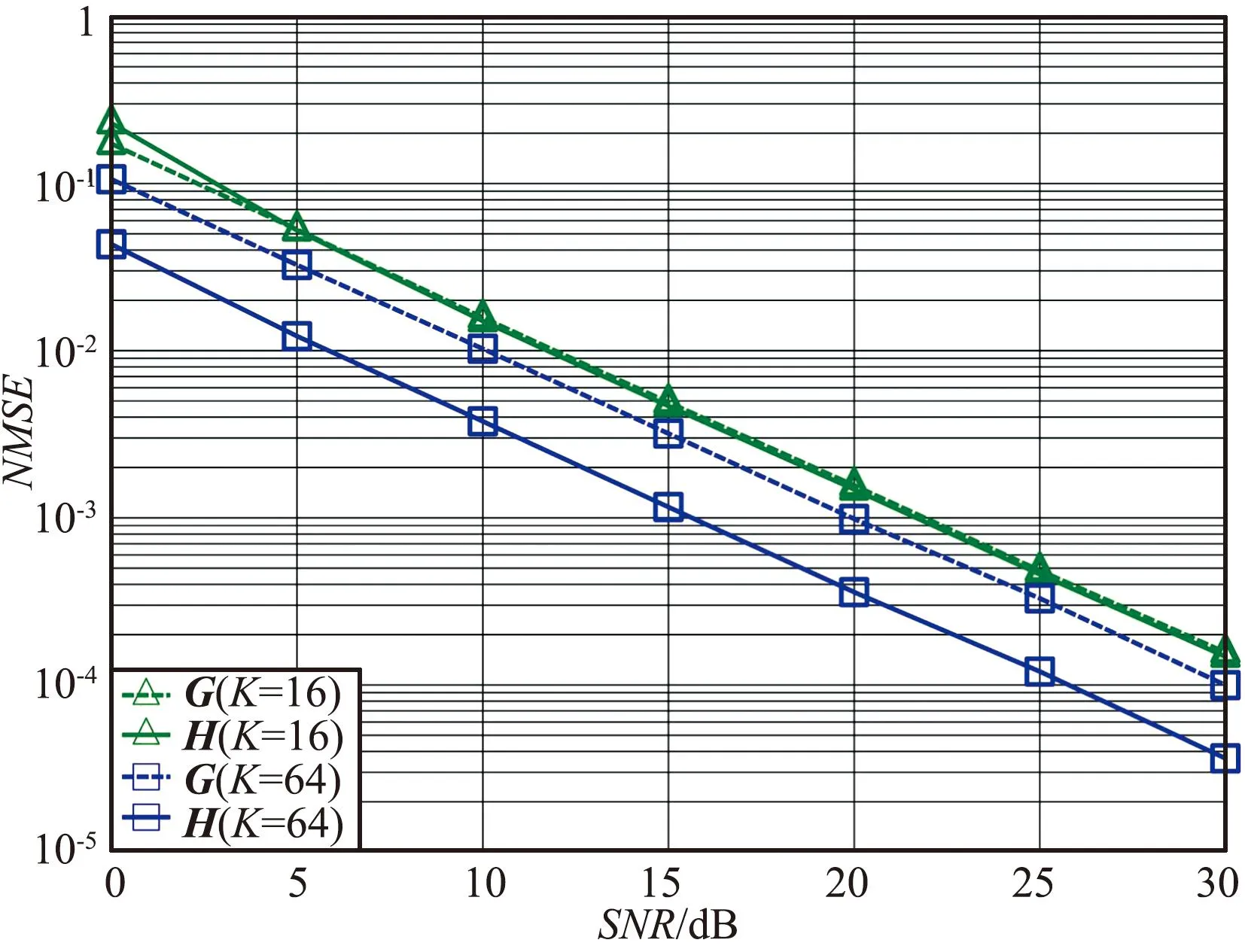
图3 不同K值下NMSE性能与SNR之间的关系Fig.3 Relationship between NMSE performance and SNR for different values of K
假设K=32,M=N=T=16,LG=10。图4给出了在2种不同相移矩阵个数P∈{8,16}的情况下,所提ALS算法的NMSE性能随SNR的变化。从图4可以看出,随着P值增加,信道估计精度提高,这是因为导频训练序列长度与P值成正比。
图4 不同P值下NMSE性能与SNR之间的关系Fig.4 Relationship between NMSE performance and SNR for different values of P
假设K=32,M=T=P=16,LG=10。图5展示了RIS单元个数N对所提ALS信道估计算法估计精度的影响。图5中N∈{16,20},结果表明随着N值增加,信道估计精度逐渐降低。这是因为增加N意味着增加了信道维度,导致G和H中需要估计的信道系数增多,从而使信道估计性能下降。

图5 不同N值下NMSE性能与SNR之间的关系Fig.5 Relationship between NMSE performance and SNR for different values of N
4 结束语
利用PARAFAC分解,本文为RIS辅助的mmWave多用户波束空间MIMO通信系统提供了一种新的信道估计思路。具体而言,通过充分挖掘BS接收导频信号的张量结构,本文提出一种新颖的ALS信道估计算法,此算法能够得到信道估计闭式解,从而准确估计BS与RIS以及RIS与用户之间的信道。本文给出ALS 信道估计算法的可行性条件,该条件为系统参数选择提供了理论指导。同时,仿真实验讨论了BS天线数、RIS相移矩阵个数以及RIS单元个数对信道估计性能的影响。从不同的仿真实验结果可以验证,所提ALS算法具有良好的信道估计性能。
