基于ICA的锂电池SOH估计曲线确定方法研究

王晗蕊, 陈则王, 徐肇凡

(南京航空航天大学 自动化学院,江苏 南京 211106)

0 引言

现阶段全球资源日益短缺、气候日益恶化,为了缓解环境压力,新能源技术飞速发展[1]。锂离子电池具有体积小、效率高以及寿命长等诸多优点[2],在航空航天和电动汽车[3]等领域具有广阔的应用前景。

锂电池的健康状态(SOH)体现了现阶段电池与原始电池性能的比较结果[4],其中基于数据驱动的SOH估计利用直接或间接影响电池老化的健康特征来实现[5]。在数据驱动方法实现过程中,如何提取有效的健康特征是研究的重点与难点[6]。现阶段锂电池的健康特征主要分为直接的健康特征与间接的健康特征。锂电池的衰退过程中伴随着容量的衰减和内阻的增加,因此可将容量与内阻作为直接健康特征[7]。但在实际的应用过程中,容量数据无法直接获得,需要通过安时积分法[8]进行计算,不仅费时而且需要对电池进行完全的充放电。与此同时,内阻通过电化学阻抗谱仪获取,需要专业人员测量,成本较高。而间接的电池健康特征更容易获得,且与电池的健康状态密切相关[9]。Eddahech等人[10]直接从恒流曲线和恒压曲线上提取特征,然后代入智能算法中实现对锂电池的健康状态估计。杨柯等人[11]使用等压升充电时间、等流降充电时间、等压降放电时间和等时间电压差四个健康因子对锂电池进行健康状态估计。但是传统的充放电曲线在不同循环下并不存在显著差异,用其获得的健康特征并不能反应电池内部复杂的化学变化,这会导致一些能够反应电池内部变化的信息丢失。相比上述的间接健康特征,采用本文提出的容量增量曲线分析方法在获取电池内部复杂工况关键信息的同时,具有更高的灵敏度。

虽然容量增量分析法可以通过IC曲线直观反映锂电池内部产生的化学变化,但基于锂电池的端电压与瞬时容量直接获取的IC曲线存在大量噪声,不利于特征提取。

Li等人[12]从滤波后的IC曲线上提取特征,然后基于高斯回归(Gaussian Process Regression, GPR)模型来实现锂电池的SOH估计。杨胜杰等人[13]使用容量增量曲线上提取的特征参数进行锂电池的健康状态估计。该过程采用高斯过程回归建立锂电池的SOH估计模型。上述文献在取得IC曲线的过程中,采样间隔和滤波器的窗口大小属于主观选择,对提取的健康特征的客观性不能保证。并且不存在最优的滤波器,一次充电的滤波参数未必适用于另一次充电过程。

综上,现有的基于容量增量分析的锂电池健康状态估计方法存在以下几点问题:(1)原始IC曲线包含太多噪声,不能直接用来估计锂电池的SOH。如果采用滤波的方法平滑IC曲线,需要对采样间隔和滤波器的窗口大小谨慎设置;(2)使用滤波的方法对IC曲线的平滑度和特征保持率缺乏客观性,这两者对特征提取至关重要;(3)很难选择最优的滤波器来平滑IC曲线,因为一个充电过程的调谐参数可能不适用另一个,特别是锂电池接近寿命时。

为了解决上述问题,本文提出一种新的基于RL-VC模型的容量增量分析的锂电池SOH估计方法。使用不同化学成分的锂电池建立RL-VC模型,探索作为SOH估计基础的IC曲线的准确性和稳健性。将RL-VC模型与传统滤波方法在IC曲线的变形和特征提取的客观性上进行对比,来保证IC曲线的平滑度和特征保持率;并通过试验验证本文所提方法的可行性。

1 传统滤波与RL-VC模型

1.1 传统滤波算法

IC曲线可以提供有关电池老化机制和SOH的关键信息,传统方法通过选择合适的滤波器获得IC曲线。获得IC曲线分为两个步骤:(1)画出原始IC曲线;(2)对原始IC曲线进行滤波达到降噪的目的。上述两个步骤都包含主观参数的调整,不能保证锂电池IC曲线的确定性。而本文使用的容量增量分析法,基于微分原理,将变化缓慢的端电压-容量(V-Q)曲线,转换成变化更明显的端电压-容量变化率曲线(V-dQ/dV),根据曲线提取电池的老化特征[14]。当锂电池处于恒流恒压的工况下,以充电工况为例,IC曲线由对V-Q等式进行微分得到,具体计算式如下:

Q=It

(1)

V=f(Q),Q=f-1(V)

(2)

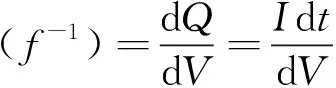
(3)

式中:Q、V、I分别为电池的容量、端电压、充电电流;t为充电时间;f为Q-V的关系表达式。

使用差分方程对上述微分方程进行近似以简化计算过程,即用固定电压间隔ΔV代替dV,具体的计算式如下:

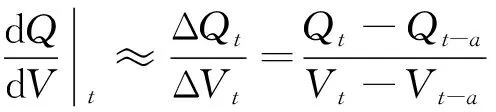
(4)

式中:Qt为电池的瞬时容量;Vt为电池的瞬时端电压;a为用户自定义的采样间隔,可以对原始的IC曲线进行粗略的平滑。

在此基础上,选择一个合适的滤波器对IC曲线进行进一步降噪,以方便后续提取IC曲线的健康特征。其中,关于滤波器的选择以及相关滤波器参数的选择具有一定的主观因素。

1.2 RL-VC模型

传统方法是通过设置等间隔的dV获取IC曲线,在设置不同dV的同时,对应曲线的峰值也会随之变化,且随着dV增大,峰值逐渐减小。针对上述问题,本文通过洛伦兹函数进行峰值拟合获取IC曲线,可以实现对IC曲线峰值的定量分析[15]。具体见表达式(5):

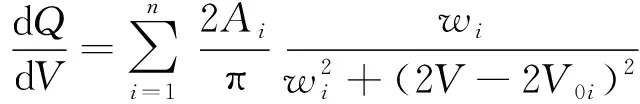
(5)

式中:n为IC曲线中峰值的数量;Ai为第i个峰的峰面积;wi为第i个峰在半高处的峰宽;V0i为第i个峰值对称中心处的电压。

与此同时,式(5)中涉及参数与锂电池内部的材料级相变动力学有十分密切的关系:V0i为锂电池发生相变的氧化还原电压;wi为相应转变过程中半高处的全宽度;Ai为活性材料在相变过程中的累积电荷[16]。但在实际应用中,只有电流和端电压可以直接测量,为了便于直接校准,对式(5)进行积分运算,可以消除对采样频率、分辨率以及噪声分量的敏感性:

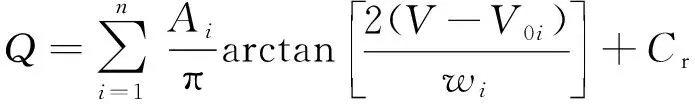
(6)

式中:Cr为积分后的残差[17]。

基于此,在相同的模型框架内对式(6)进行调整,得到RL-VC模型的表达式为

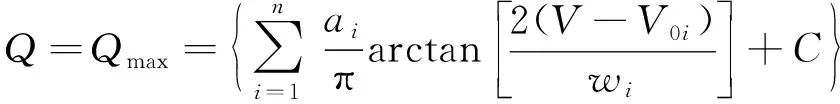
(7)

式中:Qmax为恒流充电容量的相关值;ai为第i个峰值的面积权重;C为积分常数。

尽管有类似表达式,RL-VC模型可以预期增强对参数边界的误差容限。

1.2.1 RL-VC模型参数识别

式(7)中涉及的参数需要通过参数识别来确定,以实现预期拟合精度。其中n是由锂电池中阳极和阴极的材料属性决定的。本文采用非线性最小二乘法对式(7)进行参数识别,同时利用基于内反射牛顿法的子空间信赖域方法[18]对建立的非线性最小二乘问题进行求解。

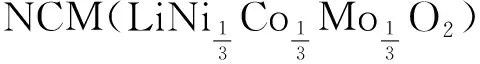
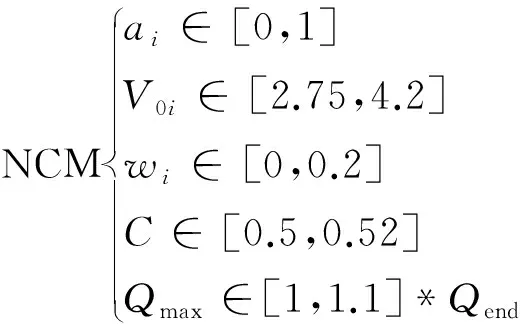
(8)

自主搭建的试验平台使用电池参数边界如式(9)所示。该电池表现出两个明显可测的IC峰,峰值个数n设置为2。

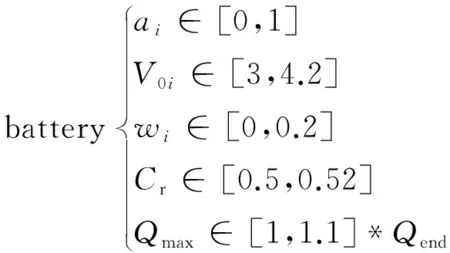
(9)

为了求解RL-VC模型,根据上述定义的约束建立非线性最小二乘方程得到具体的模型参数。非线性最小二乘法原理见式(10)和式(11),即求得向量x使下述表达式取得误差平方和最小值,x是局部最小值:

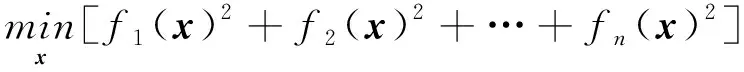
(10)

(11)

式(10)和式(11)中向量x存在于一个区间内,本文采用基于内反射牛顿法的子空间信赖域反射法来解决该非线性最小二乘问题。式(10)和式(11)中的x是一个向量,对应RL-VC模型中的未知参数ai、V0i、wi、Cr、Qmax,参数中的i由峰值个数n决定,未知数的个数决定x向量的维数。基于非线性最小二乘法的参数识别是通过调用MATLAB中的lsqnonlin函数来实现的。

2 试验验证

2.1 试验平台

本文搭建的锂离子电池独立试验平台由硬件和软件两部分控制系统构成。硬件系统部分主要包含计算机、锂电池充放电控制电路、数据采集卡、信号检测电路以及恒温箱等试验设备。软件控制模块实现数据采集与处理、充放电试验过程控制。试验测试硬件平台结构见图1,实际搭建的实物平台见图2。

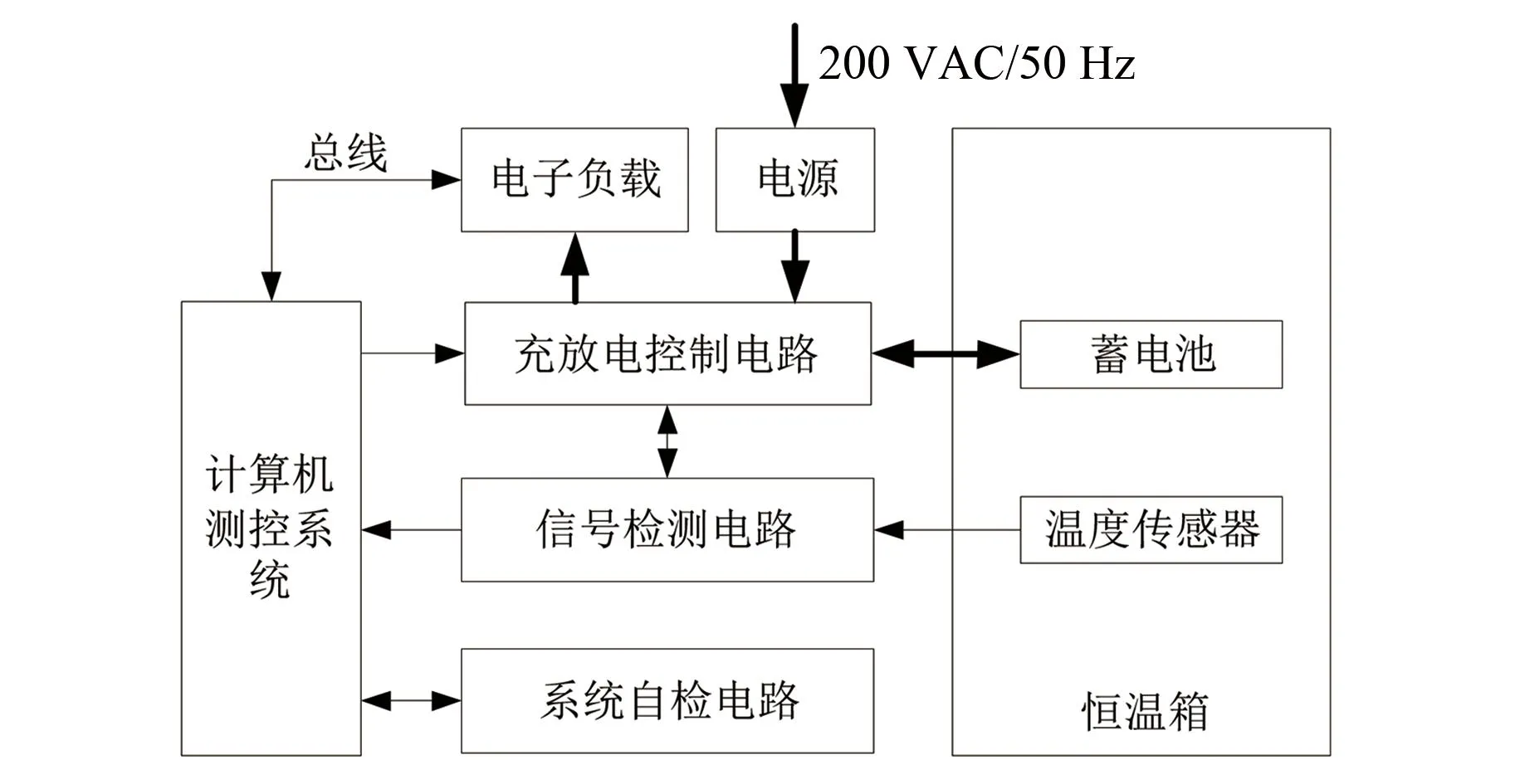
图1 试验测试硬件平台设计结构Fig.1 Design structure of test hardware platform

图2 试验实物平台Fig.2 Test physical platform

2.2 试验数据

2.2.1 自主搭建试验平台试验数据

本试验使用的锂电池选用三星ICR18650-22FM钴酸锂电池。该电池具体参数见表1。

表1 ICR18650-22FM电池参数Tab.1 ICR18650-22FM battery parameters

(1) 充电过程:

将恒温箱的温度设置为24 ℃,使用1C的倍率对锂电池进行恒流充电。当锂电池的电压增加至最大截止电压时,将恒流充电模式转换成恒压充电模式。当充电电流下降至110 mA时,停止充电。

(2) 放电过程:

1号电池以2C的倍率恒流放电,2号电池以1C的倍率恒流放电。当电池的电压降至最小截止电压时,停止放电。

上述(1)、(2)充放电过程组成一次标准的充放电循环,然后不断重复上述步骤,采集电池的电压、电流等试验数据。此外,本文还使用NASA提供的动态数据集NCM进行对照试验,进一步表明本文方法的有效性。

2.2.2 NCM数据集

NCM数据集由NASA提供,其中RW3、RW4、RW5以及RW6四个18650型电池为一组。具体的随机行走(Random Walk)循环方式如下:从集合{-4.5 A, -3.75 A, -3 A, -2.25 A, -1.5 A,-0.75 A, 0.75 A, 1.5 A, 2.25 A, 3 A, 3.75 A, 4.5 A}中随机挑选一个电流进行充电或者放电,其中正数为放电,负数为充电。当锂离子电池在所选的电流下,端电压降至3.2 V或者升至4.2 V,或者在该电流下工作了5 min,电池休息1 s,然后进行下一个随机充/放电过程。其中,每50个随机充/放电循环后,进行一次标准的充放电试验。本试验采取随机行走的充电过程,来模拟真实工况下锂离子电池的老化过程。

3 结果分析

要利用ICA进行锂离子电池的SOH估计,首先得作出关于锂离子电池的IC曲线,然后提取健康特征。本文对自主搭建试验平台获得的试验数据以及NASA中NCM动态数据集分别进行试验,分别基于预滤波以及RL-VC模型获取对应的IC曲线,并进行对比分析。

3.1 基于传统滤波方法

图3是自主试验平台获得的1号电池数据在恒流充电工况下第2次充放电循环下的原始IC曲线。该曲线存在明显噪声,无法直接提取电池的老化特征。

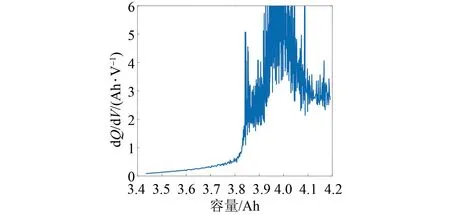
图3 原始IC曲线Fig.3 Raw IC curves

移动平均滤波器(Moving Average Smoothing Filter, MASF)使用固定宽度移动窗口并对窗口内的数据计算均值来实现滤波。如图4(a)所示,分别是使用窗口宽度为80、100、150、200、250的MASF滤波器得到的第2次循环下的IC曲线。从图4(a)中观察到随着MASF滤波窗口宽度的不断增加,IC曲线的波形逐渐失真。当滤波窗口宽度为80时,IC曲线存在明显噪声。当滤波窗口宽度增加至200时,峰值明显衰减甚至有消失的趋势。当滤波窗口宽度处于150～200区间内,虽然波形的完整性较好,但是峰值的衰减程度不同不能保证IC曲线的确定性。为了观察MASF的最佳参数是否随着电池的老化程度产生高度不确定性,本文使用相同的滤波器参数在1号电池的第8次充放电循环过程拟合IC曲线,试验结果见图4(b),表明相同的滤波参数在不同循环次数下的拟合效果也不相同。

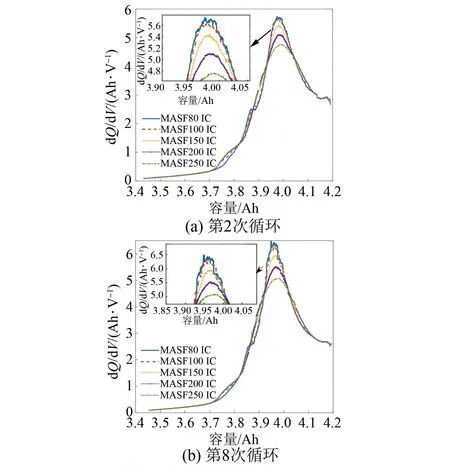
图4 MASF滤波结果Fig.4 MASF filtering results

使用MASF获得的IC曲线容易被窗口中的极值点影响,存在部分的信息丢失,为了使得作为对比的传统滤波方法结果更为客观,本文同时使用高斯平滑滤波(Gaussian Smoothing Filter,GSF)处理IC曲线。GSF根据高斯函数取得数据的加权平均值来实现滤波,其表达式为

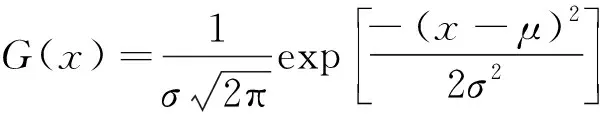
(12)

式中:x为输入数据;σ为控制滤波窗口大小的标准差;μ为均值。

为了与MASF进行对比,GSF的滤波窗口宽度同样选择了80、100、150、200、250。图5(a)和图5(b)分别是1号电池第2次和第8次循环充放电数据,该图表明GSF的滤波效果较MSF的滤波效果好,但波形同样随着滤波窗口宽度的增加出现明显失真,峰值明显衰减,不能保留IC曲线的重要特征。

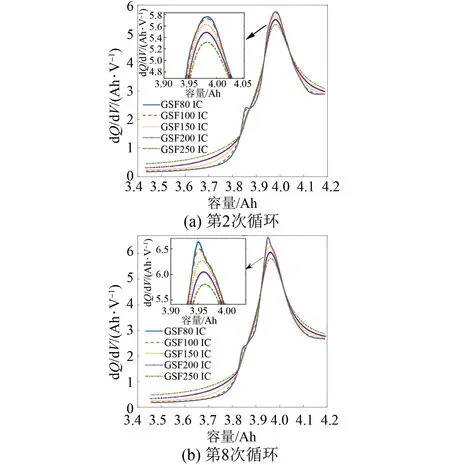
图5 GSF滤波结果Fig.5 GSF filtering results

上述试验结果表明,使用同样的MASF与GSF滤波器参数时,第2次的IC曲线相比于第8次的IC曲线,波形失真度与峰值衰减度明显减轻,说明MASF和GSF最佳参数随着电池老化产生了高度不确定性。相反基于VC模型的方法,通过基于原始IC曲线数据的拟合误差平方和最小化来保证最优性,不用加任何基于规则的约束。

3.2 基于RL-VC建模方法

所提方法可以概括为以下步骤:

步骤1:首先根据所研究电池的化学性质确定式(9)、式(10)给出的模型阶数和参数边界。

步骤2:建立的RL-VC模型用于拟合原始Q-V曲线,该数据通过恒流充电过程中的电流和端电压测量获得。

步骤3:对该模型的性能进行评价,即计算拟合模型与电池实际容量之间的平均绝对误差(Mean Absolute Error, MAE)。

步骤4:对获得的Q-V曲线进行微分,获得电池在不同循环次数下的IC曲线。

本节分别建立了1号电池和NCM数据集的RL-VC模型,并对模型的性能进行评估。评估标准采用平均绝对误差:

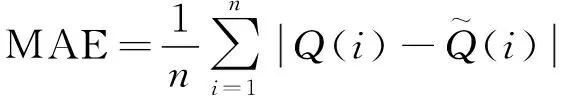
(13)

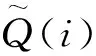
3.2.1 基于自主搭建试验平台数据

根据前文所述,试验平台中的1号电池n设置为2,该VC模型存在8个未知数。解出VC模型的参数后,对建立的RL-VC模型性能进行评估。通过建立RL-VC模型对锂离子的电池容量进行拟合,拟合结果见图6(a)。图6(a)中可以看出,曲线基本吻合,说明可通过RL-VC建模的方法拟合锂电池的真实容量。具体的拟合误差见图6(b),可知平均绝对误差范围在0.03 Ah以内,容量建模误差在0.23%以内。

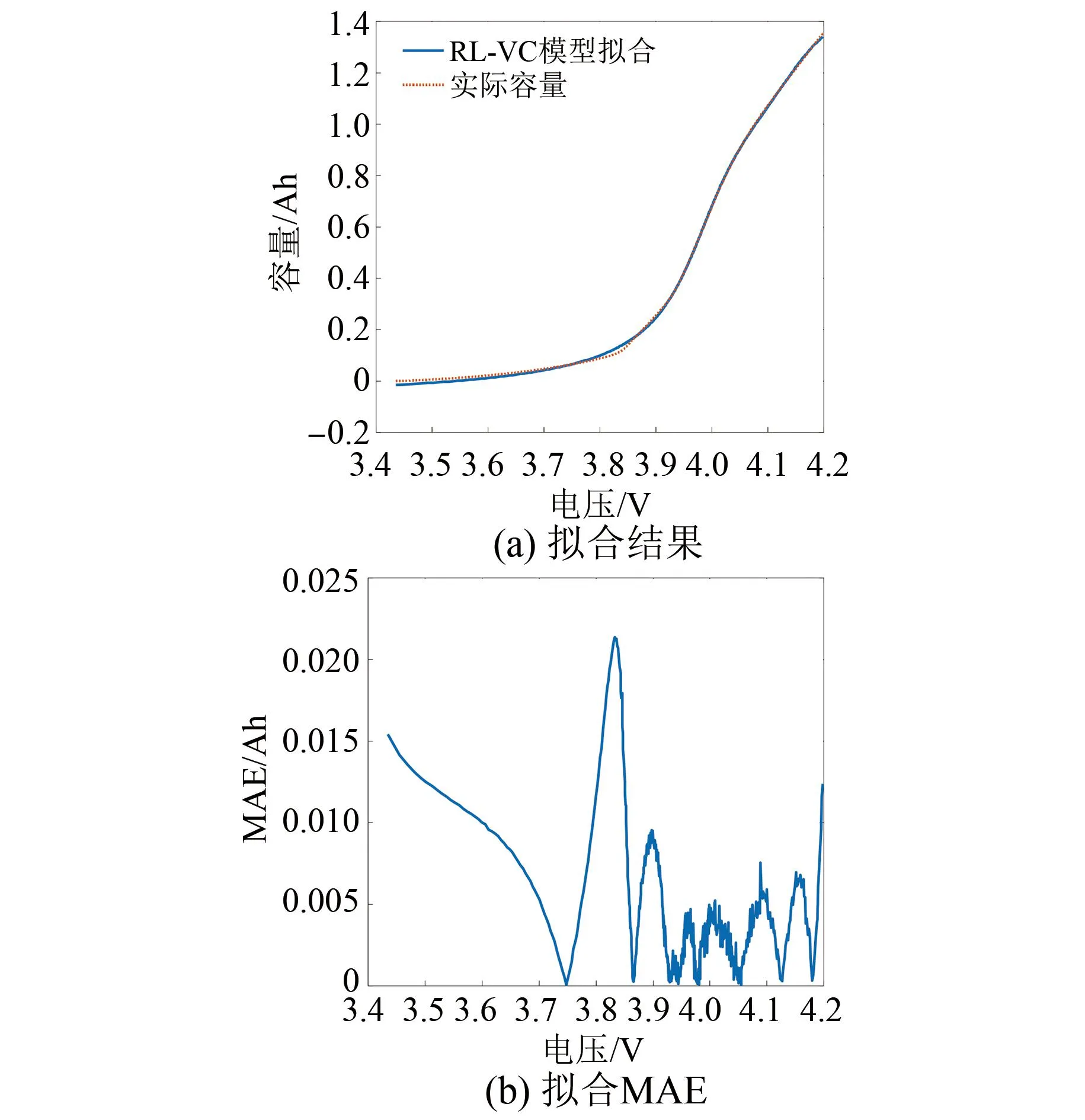
图6 RL-VC模型Q-V曲线拟合结果Fig.6 RL-VC model Q-V curve fitting results

根据VC模型建立第2、8、15、20和25次充放电循环下的IC曲线,试验结果见图7。图7中第2次循环下的IC曲线与图4(a)形成对比,图7中的第8次循环下的IC曲线与图4(b)形成对比。可以观察到,当使用传统滤波方法获得IC曲线时,不同的滤波方法和相同滤波方法不同的滤波窗口都会导致IC曲线的峰值出现明显的区别。而相比于图4、图5的传统滤波方法下的IC曲线,图7中所有曲线均保留完善的电池老化特征,在一定程度上反映了锂电池内部复杂的化学变化。IC曲线避免了传统滤波方法中的主观性和不确定性,且计算量相对适中。同时一次循环中设置的建模参数同样适用于其他循环过程,对电池老化具有高鲁棒性。本文提取了图7中的曲线峰值,观察其与锂离子电池的关联性,结果见图8。从图中可以看出峰值与电池容量之间存在高度线性关系,为后续进行锂电池的SOH估计奠定了基础。

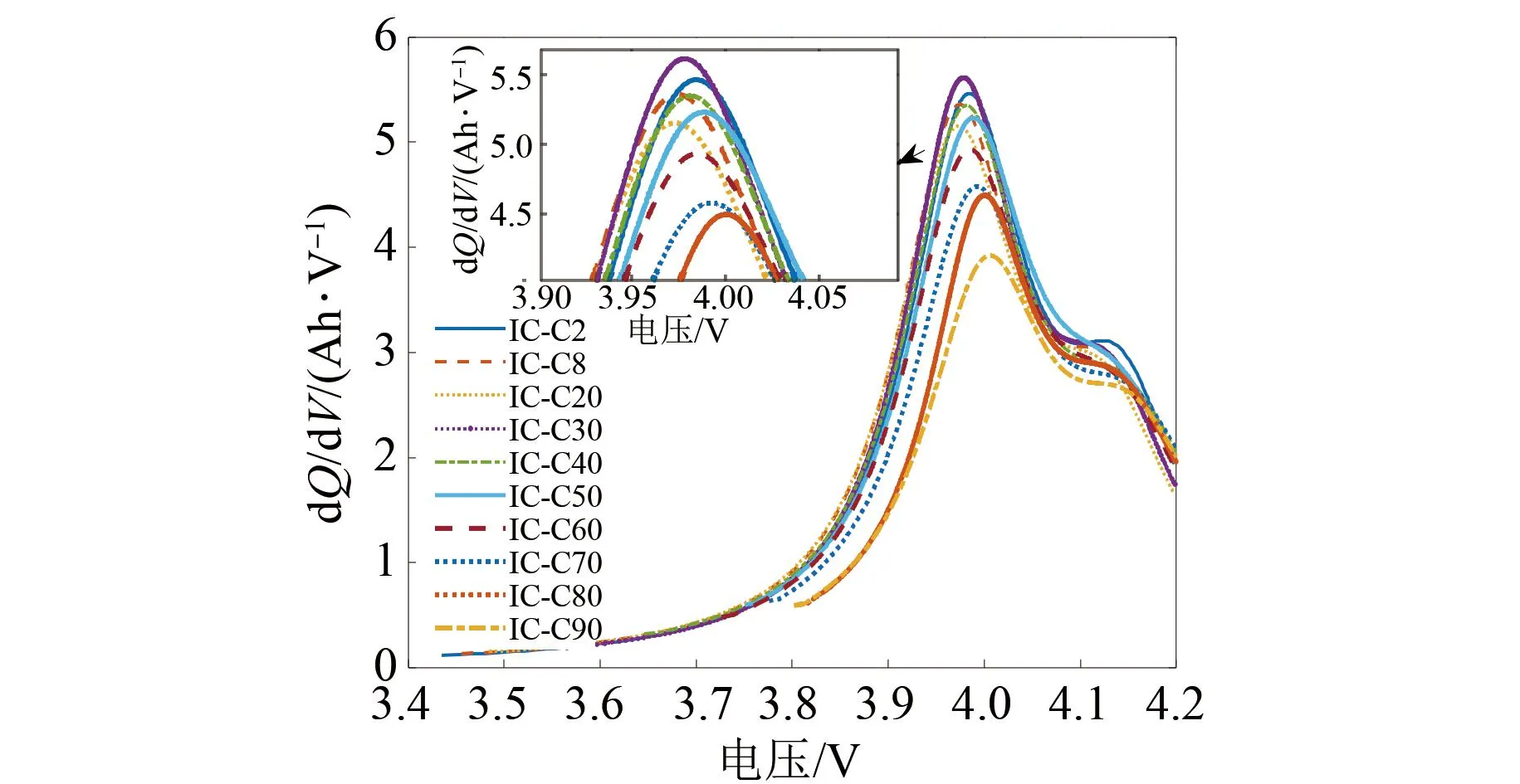
图7 不同循环下的IC曲线Fig.7 IC curves under different cycles

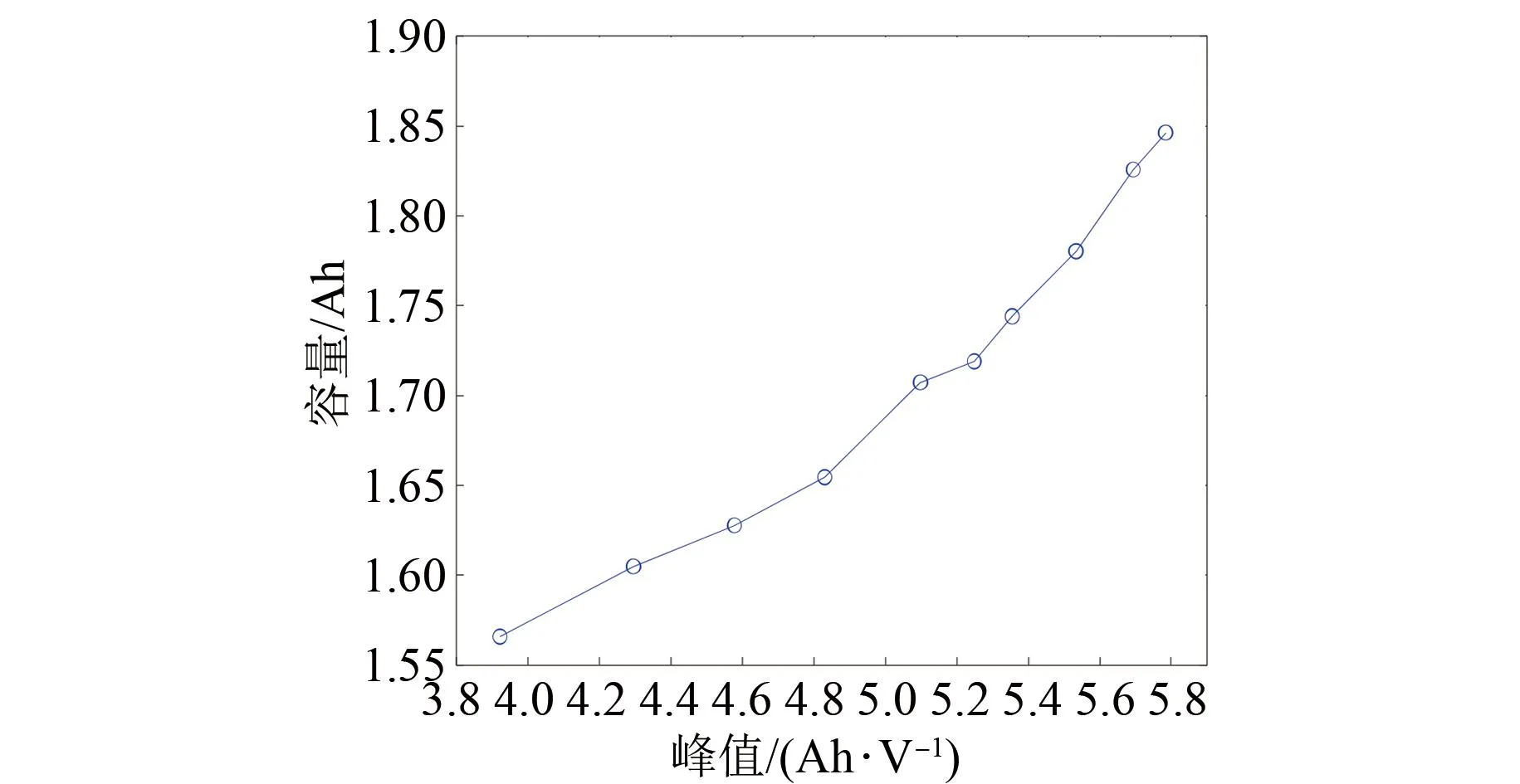
图8 峰值与电池容量关系Fig.8 Peak versus battery capacity

3.2.2 基于NCM数据集

现阶段,针对锂离子电池在动态条件下进行实时健康状态估计是一项巨大挑战。目前大部分锂离子电池的容量估计局限于固定充放电的锂电池试验数据集,很少使用更接近于实际情况的随机充放电的老化数据集。为了验证本文提出的RL-VC模型的性能,本文采用NASA数据集中的随机充放电模式下的数据集在基于RL-VC模型的基础上进行容量增量分析(ICA),可以在一定程度上反应锂电池在现实复杂工况下的容量变化。

根据前文VC模型的参数识别,NCM电池的n设置为3,该模型共含有11个未知数。根据该VC模型拟合的电池容量、实际电池容量与锂电池端电压的关系见图9(a)。之后对建立的RL-VC模型进行性能评估,计算拟合的平均绝对误差。从图9(b)中可以看出,平均绝对误差在0.05 Ah以内,容量建模误差在0.16%以内,说明该VC模型有较好的拟合效果。根据VC模型作出的IC曲线见图10。本文提取了根据RL-VC模型所作IC曲线的峰值,其与电池实际容量的关系见图11,从图中可以观察到峰值与电池容量之间有很强的线性相关性,有利于之后对锂电池的SOH进行估计。

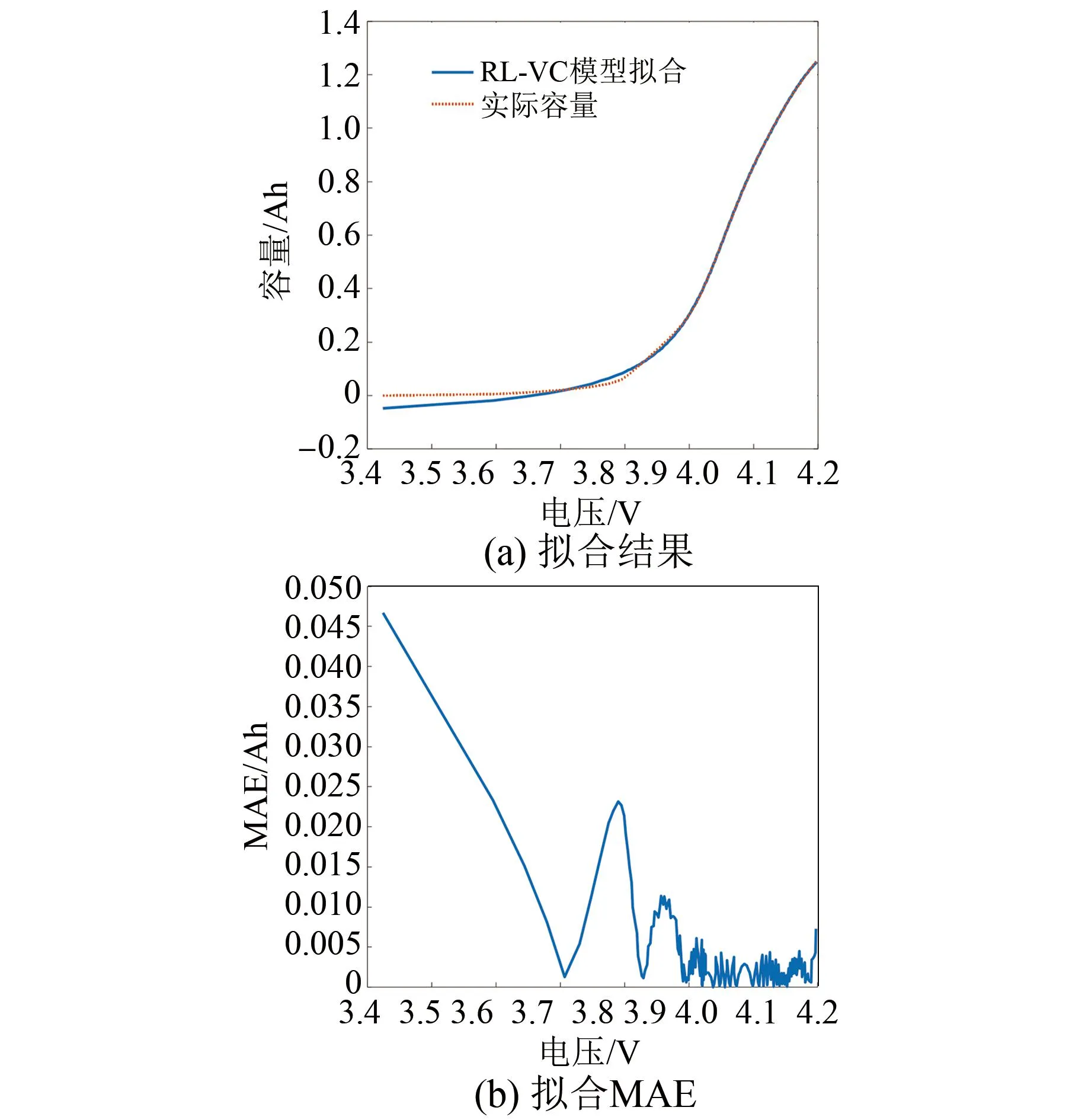
图9 RL-VC模型Q-V曲线拟合结果Fig.9 RL-VC model Q-V curve fitting results

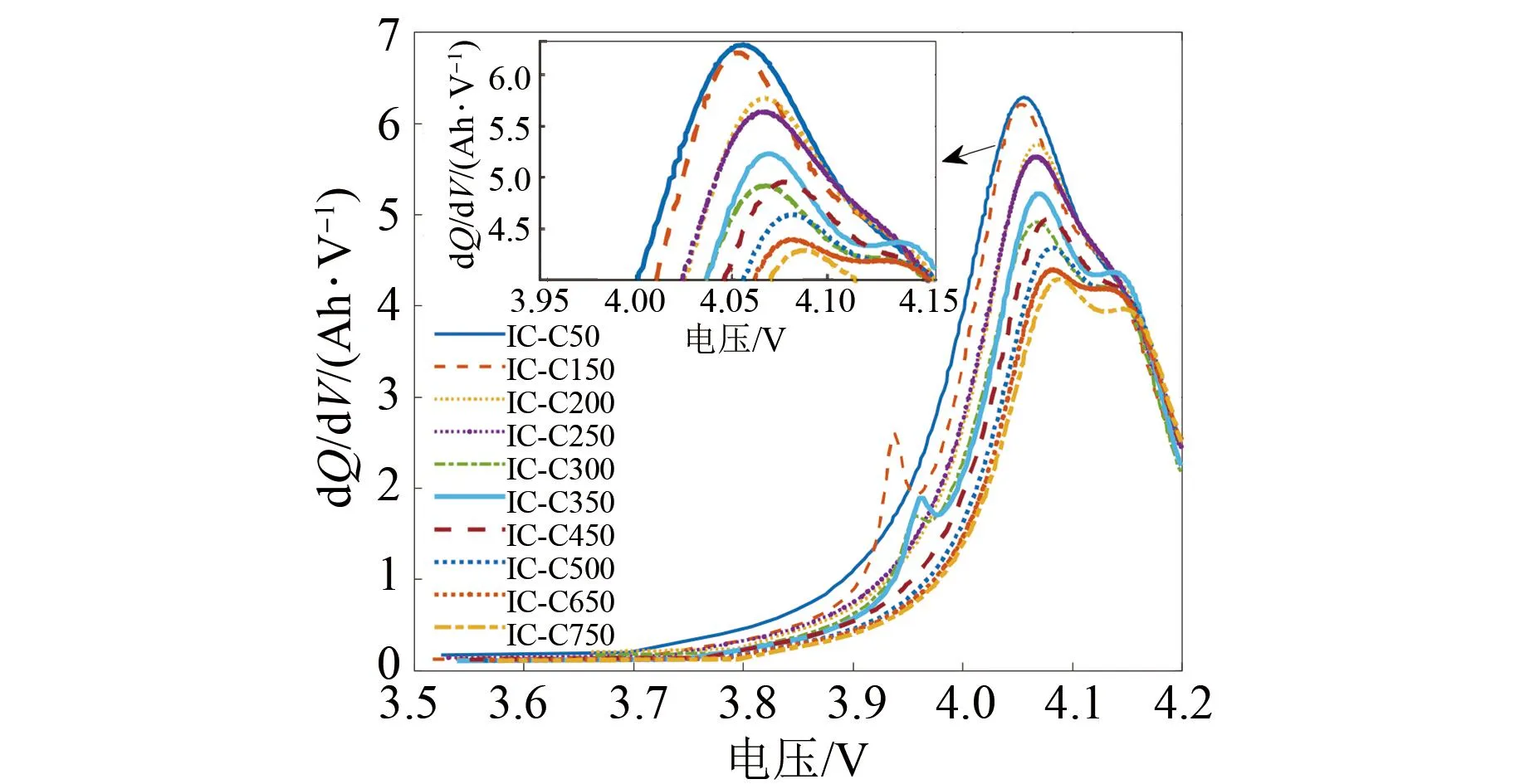
图10 不同循环下的IC曲线Fig.10 IC curves under different cycles

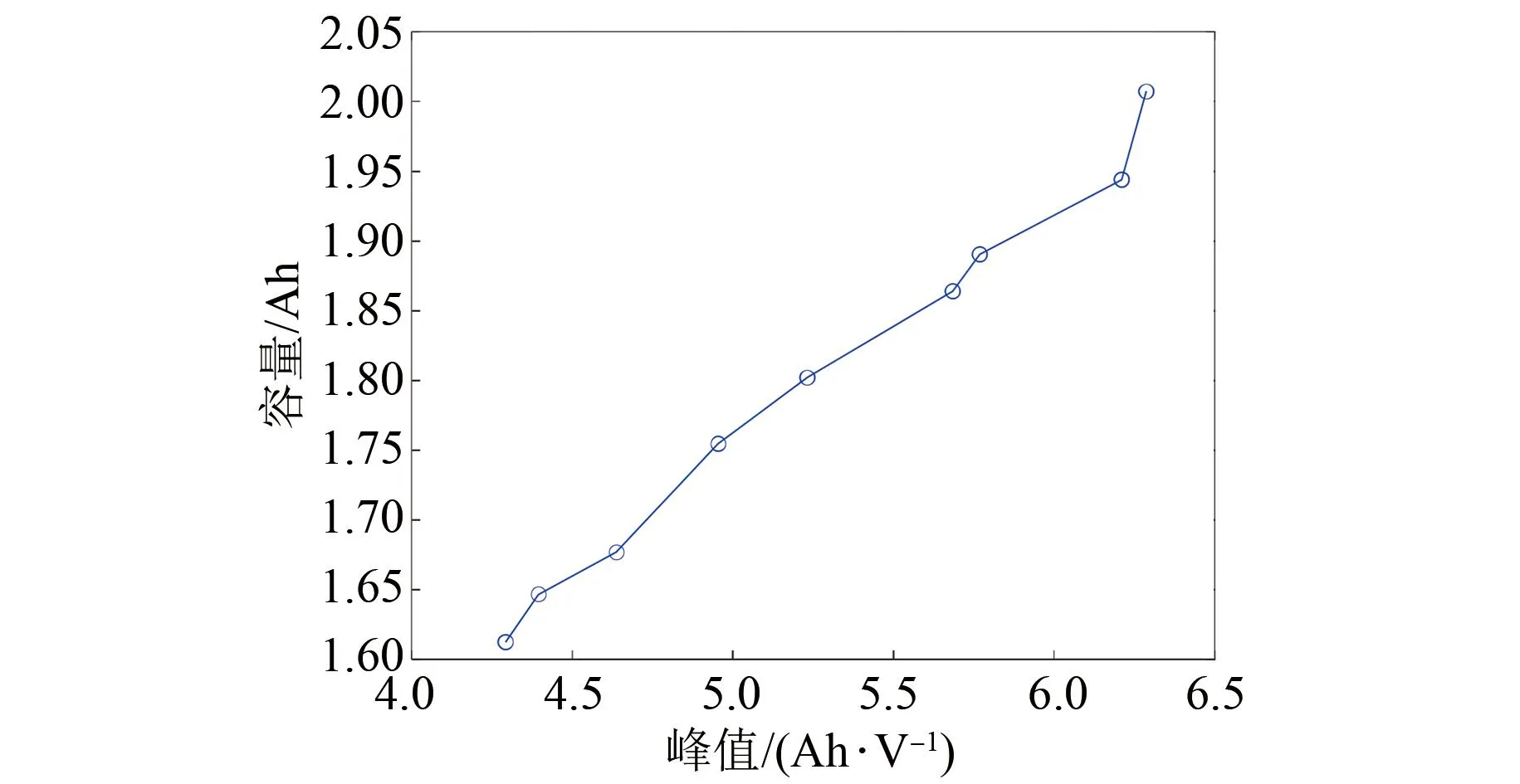
图11 峰值与电池容量关系Fig.11 Peak versus battery capacity

针对上述1号电池和NCM两种类型数据集建立RL-VC模型,基于实际的电化学机理确定n。但如果增加n的个数会对后期锂电池的SOH估计造成负面影响,因为增加多余的微弱峰,不仅增加了模型的计算成本,而且可能会造成过拟合现象,造成在IC曲线上提取的特征可靠性降低。

4 结语

本文提出了一种基于RL-VC模型的锂电池IC分析方法。本文的主要研究方案和成果如下:(1)使用传统滤波方法时,对于一个特定的循环去处理另一个循环,该滤波所设置的参数将失去最优性。与传统滤波方法相比,基于RL-VC模型对电池老化具有高鲁棒性;(2)本文提出的RL-VC模型通过比较简单的参数化模型来获得,相比传统滤波方法不需要大量的后处理来提取特征,计算量也相对适中,同时也避免了主观性和不确定性;(3)采用RL-VC模型对1号电池和NCM两种不同类型的数据集进行分析,可知容量建模误差分别在0.23%和0.16%以内。并且根据RL-VC模型作出的IC曲线提取的特征与电池容量高度线性相关,为后续锂电池的SOH估计奠定了基础。