多无人机辅助NOMA网络的联合无线资源分配算法

邵鸿翔，孙有铭，冀保峰，韩 哲，，刘云卿

(1.洛阳理工学院 计算机与信息工程学院，河南 洛阳 471023；2.中国人民解放军 61062部队，北京 100089；3.河南科技大学 信息工程学院，河南 洛阳 471023)

0 引言

5G和B5G(Beyond-5G)网络中,在数据高速率和低时延应用需求急剧增长的推动下,功率域非正交多址(Non-Orthogonal Multiple Access, NOMA)成为一种很有前途的多址技术[1-2]。NOMA可支持多个用户在同一正交资源内同时传输,接收端采用逐次干扰消除(Successive Interference Cancellation, SIC)技术对接收到的信号进行解码。与传统的正交多址(Orthogonal Multiple Access, OMA)技术相比,NOMA能有效提高频谱效率和能量效率,允许更多用户连接到所需的网络。

近年来,无人机(Unmanned Aerial Vehicle, UAV)因其具备高机动性、易于部署和高概率视距传播引发的高速率等特点备受关注。UAV辅助移动通信系统的研究可有效应对地面基站过载、突发灾害和紧急事件的通信增强和恢复[3]。UAV通信网络将是未来6G空天地一体化网络融合的关键组成部分,在战场侦查、野外救援和物联网信息传输等民用和军用领域发挥重要作用[4]。将NOMA引入UAV辅助移动通信系统,可实现终端接入数量的增加、用户服务质量(Quality of Service, QoS)的提升和无线通信中频谱短缺问题的缓解。

目前,对功率域NOMA的用户配对和功率分配方案的研究已取得了许多成果。文献[5]根据下行NOMA网络中用户的目标速率要求,提出了一种分布式强/弱用户配对和功率分配算法。文献[6]考虑了最小速率约束,提出了一种实现下行NOMA网络中和速率最大化的封闭式最优用户配对解决方案。文献[7]提出了一种基于NOMA网络的分布式群组切换用户配对方案,在考虑需求多样性的情况下,最大限度地提高用户体验质量。以上研究只考虑单一基站场景,未考虑多UAV场景和其机动性对NOMA网络中的资源分配带来的挑战。近年来,面向NOMA的UAV辅助通信网络系统级资源分配优化研究受到广泛关注[8-15],如能量和频谱效率[9,11],UAV轨迹[10,14],位置和功率联合优化[12-13],分组和功率联合优化[15]。文献[8]研究了利用周期性NOMA和UAV轨迹联合优化多用户通信调度,使地面用户最小吞吐量最大化。文献[9]考虑用户的多重QoS,从能效角度研究了UAV基站最优高度的NOMA方案。文献[10]研究了基于NOMA通信和能量收集的UAV辅助合作认知无线网络的最大吞吐问题。文献[11]研究了在UAV位置和功率约束下的辅助全双工非正交多址(FD-NOMA)系统的能量效率最大化问题。文献[14]研究了NOMA/OMA混合模式下的轨迹优化问题,实现UAV辅助通信系统中上行/下行链路平均数据速率最大化。文献[15]提出了基于图论最大割定理和辅助变量法的用户分组功率分配联合优化方法,实现了UAV-NOMA系统和速率的提高。然而,上述研究大多集中在单一UAV场景,仅关注单个UAV的能效和少量UAV间干扰,缺乏多UAV辅助通信NOMA网络的多维联合资源分配方法研究。本文的主要贡献如下:

① 研究多UAV空中辅助基站(Flying Base Stations, FBSs)和多地面站(Ground Base Station, GBS)混合组网复杂场景下的坐标位置,NOMA功率分配和用户配对多维联合优化问题,给出了一种从系统角度获得用户QoS提升的思路。

② 不同于文献[6,16]用户数等于信道数2倍的设定,在给定FBSs位置的多小区场景下,推导出最优的NOMA功率分配闭式解和通用NOMA用户配对方案。

③ 为最大化网络效用,将UAV的位置优化问题描述为一个局部利他博弈,证明它是至少包含一个纯策略纳什均衡(Pure Strategy Nash Equilibrium,PNE)的精确势能博弈,并设计了一种分布式学习算法以较低的复杂度找到PNE最优解。

1 模型和问题描述

图1 UAV辅助NOMA空地网络系统模型Fig.1 System model of UAV assisted NOMA air-ground network

1.1 干扰图模型

类似文献[17],利用非对称干扰图来捕捉各类型基站间同信道的复杂干扰关系。具体来说,应用广泛使用的干扰度量(Interference Metric, IM)来计算任意2个基站i和j的归一化干扰水平:

(1)

根据干扰关系,定义下面2种集合:

值得注意,不同的干扰图标准和基站间干扰关系的定义方法并不影响后续的数学推导、博弈模型的建立以及最后的结论。

1.2 问题描述

(2)

(3)

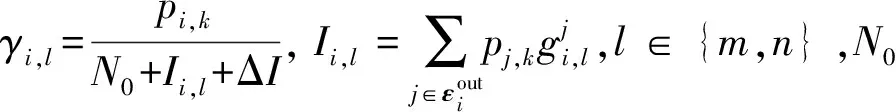
Ri(Li,PIi,αi),其中ci表示经济系数,可根据用户优先级、终端类型等设置,来刻画不同基站的权重关系;Ri表示基站i服务的所有用户速率和,Li、PIi、αi分别表示该基站的位置策略、用户配对策略和功率分配策略。为实现网络效用的最大化,考虑NOMA用户配对、功率分配和UAV位置联合优化问题,该问题可表示为:

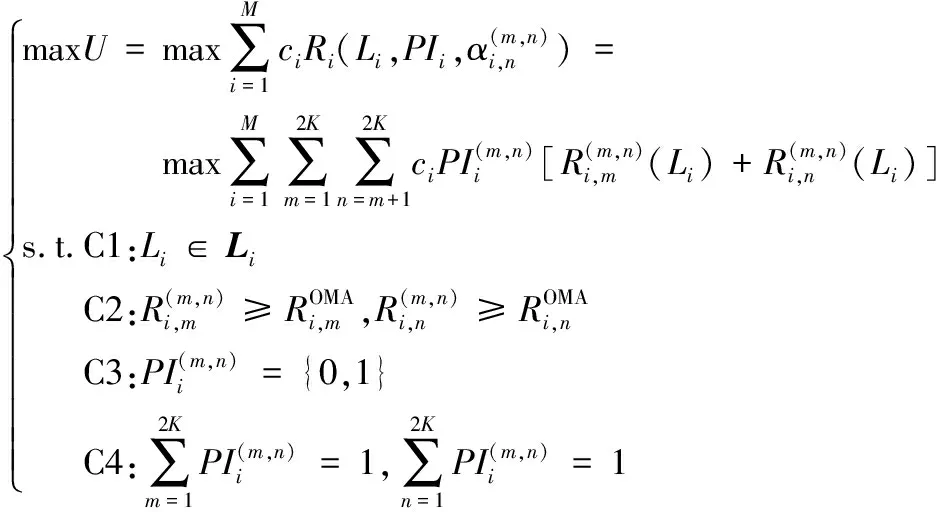
(4)

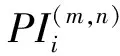
2 联合解决方案

为解决UAV辅助的多小区NOMA网络资源分配问题,提出一种复杂度相对较低的近乎最优的3步资源分配方案。首先,分析单基站场景下NOMA功率分配策略。然后,推导通用最优NOMA用户配对方案。最后,给出基于博弈的位置策略选择方法。

2.1 最优NOMA功率分配和配对策略

假设所有基站都选定其位置策略,并对一个相对简单的单基站系统来分析其最优功率分配和用户配对策略。

(5)

证明:根据式(2)和式(3),对NOMA模式接入同信道2用户的和速率求导得:

(6)

(7)

式(2)、式(3)、式(4)C2和式(7)联合可得到αn的取值为:

(8)

(9)

(10)

(11)

(12)

(13)

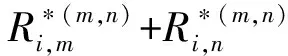
2.2 UAV基站位置优化

为了利用基站间相互作用和影响,采用局部合作博弈。不失一般性,每个基站作为一个博弈参与者是自私理性,目标都是尽可能最大化自己效用函数。运用博弈论,设计了一个具有局部合作的分布式位置优化方案。在形式上,对动态位置部署博弈建模为G=[BS,{Ai}i∈BS,GIM,{ui}i∈BS],其中BS={1,2,…,M}代表M个博弈参与者,Ai=Li表示博弈参与者基站i的策略集合,及UAV可选悬浮位置,ai∈Ai表示基站i的选择位置,a-i表示除参与人基站i以外的其他基站的位置选择策略;GIM表示网络各类基站间耦合关系的干扰图,ui表示基站i的效用函数。

类似文献[17],为获得全局最优UAV位置策略,定义博弈参与者i的效用函数为:

(14)

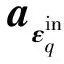
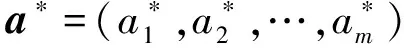
(15)

定理4:动态位置部署博弈G是一个精确潜博弈,至少存在一个纯策略NE点。

证明:首先,构造潜函数为:

(16)

根据干扰图的邻居关系,可以得到:

(17)

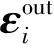
(18)

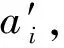
(19)

另一方面,基站i的效用函数值随其单边位置策略的改变可以表示为:

(20)

任意博弈者基站的效用函数由于其单方面改变策略发生的变化与构造的潜函数变化相同。因此,根据文献[18]对于潜博弈性质的定义,本节所提的位置部署博弈G是一个潜函数为φ的精确潜博弈。由于精确潜博弈有至少一个PNE点。所以,所提博弈G至少有一个纯策略纳什解,定理4证毕。

本文目的是最大化全网累加和速率最大。虽然从定理4知道,所提博弈至少存在一个PNE点,但是并不知道是否博弈能达到最优NE点。

定理5:全网累加和速率的全局最优解是所提博弈G的一个PNE。

根据定理5,如果能设计一个有效算法可以找到最优NE解,那将会得到式(4)所建立问题的全局最优解。

3 分布式学习算法

(21)

式中:a-i为BSi邻居的策略选择,b>0为学习参数,反映玩家的理性水平。根据文献[19],如果学习参数b足够大,CDSSA能够以任意高的概率使归一化网络容量最大化,具体执行如算法1所示。假设博弈有n个玩家,每个玩家有m种策略可选,所提CDSSA和BR算法每轮迭代的计算复杂度分别为O(nm3)和O(nm2)[20]。

算法1 CDSSA 初始化:收集定义网络范围内各类基站的位置信息、预发射功率,信道增益,根据式(1)及对应2.1节方法,构建有向干扰图模型。设置t=0,每个基站的位置策略等概率分布,及ℓaii(t=0)=1/Ai,∀i∈BS,ai∈Ai。学习算法执行过程,循环for t=1,2,…,kmax①所有基站根据其当前的策略概率分布ℓaii(t-1)选择位置策略ai(t),并与他们的“耦合”邻居基站交换信息。②第t次迭代,在干扰图中随机选择多个共存的FBS(无干扰影响的UAV可同时更新各自策略,加速算法收敛)。对于任意2个选择的FBSs i和j,它们的邻居集合εi∩εj=∅。根据式(14)和式(21)更新行动概率分布ΓAi(t)。然后,被选中的FBS根据ΓAi(t)随机选择一个动作。其他FBS的行动保持不变ai(t)=ai(t-1)。③每个FBS i感知其接入用户的信道增益,并根据式(5)和式(11)采用最优功率分配策略αoptn和用户配对PI∗(m,n)i。④如果达到了预定义的最大迭代步数kmax,则停止;否则执行步骤①。迭代结束 end for输出:博弈参与各基站的均衡位置策略和用户配对策略L∗i,PI∗i,α∗i,i∈BS。最后,计算所定义的全网效用U=∑Mi=1ciRi(L∗i,PI∗i,α∗i)。

4 仿真分析

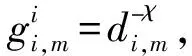
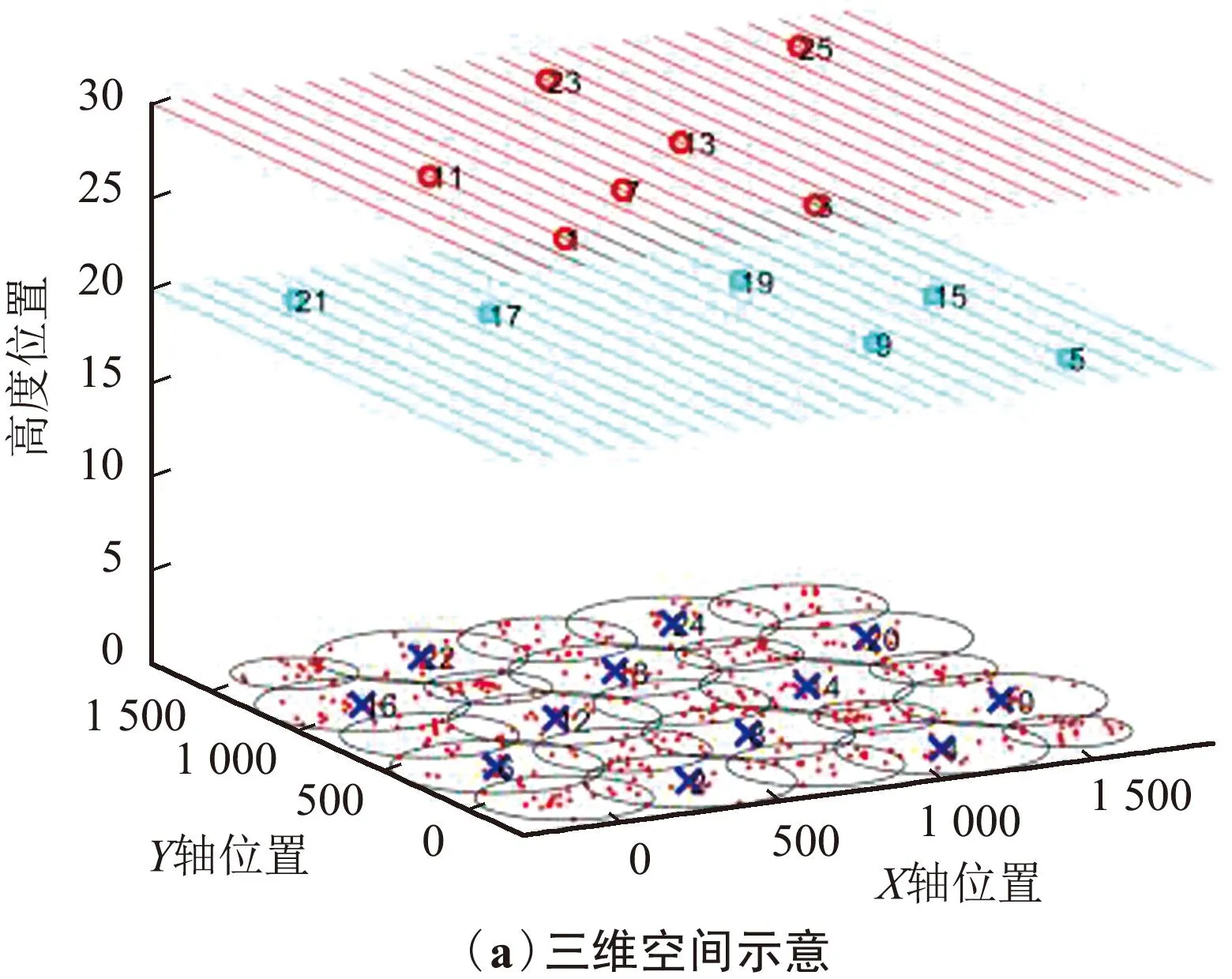
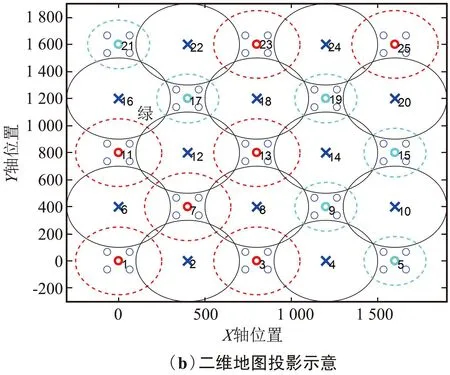
图2 5×5网格网络拓扑示意Fig.2 5×5 grid network topology

图3分别从单次结果和100次蒙特卡洛实验结果反映了所提方案的收敛性和最终可达速率。与BR算法中总是贪婪选择效用最大的更新策略不同,所提算法的位置策略更新是基于各策略效用/总和的概率向量形式,效用越大只是在下一次被选中的概率越大,而非一定会被选择,从而避免陷入局部最优。由于本文设定用户数Ui>2K,定理3所提最有配对效果优于定理2的首尾配对和随机配对。

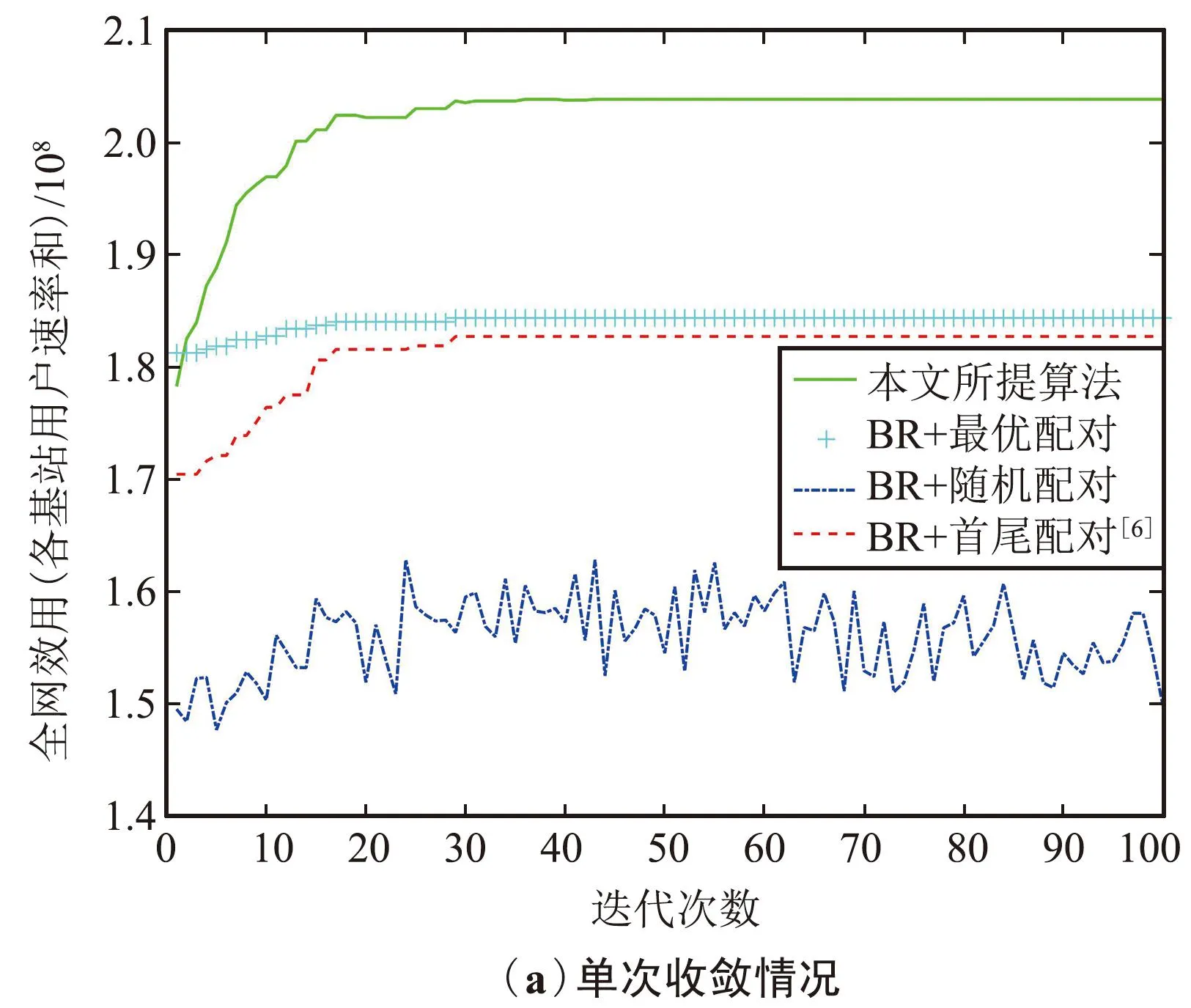
图3 所提方案的收敛性比较(用户数Ui=18)Fig.3 Convergence comparison of the proposed scheme and other algorithms(Ui=18)

从图3可看出,所提方案能够快速在40次迭代以内收敛到稳定点,并且所达网络效用优于其他方案。从平均网络效用的性能度量可以看出,所提方案与首尾配对方案和随机方案相比,性能分别提高了约14.67%和30.09%。

图4对比了不同用户数下各方案的性能。可看出在用户数大于12,及用户数大于2K时,所提最优配对方法更具优势。

图4 不同活跃用户时网络效用性能比较(K=6)Fig.4 Network utility comparison of the proposed scheme and other algorithms under different number of active users(K=6)

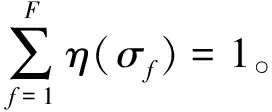
图5 不同信道状态误差下网络效用性能比较Fig.5 Network utility comparison of the proposed scheme and other algorithms under different channel errors

5 结束语

本文提出了一种最大化多UAV辅助下行NOMA网络总速率的UAV位置、用户配对和功率分配联合优化算法。在基站位置固定的多蜂窝场景下推导出最优用户调度配对和功率分配策略闭式解。在多基站网络情况下,将UAV的位置优化问题描述为一个局部利他的势能博弈,并证明该博弈模型至少包含一种PNE。为快速获得最优PNE,设计了一种分布式学习算法,最大化所定义的网络速率。仿真结果表明,该算法优于现有方案,显著提高了网络效用,并探讨了信道信息误差对性能的影响。后续研究可进一步考虑用户体验质量、各类型基站服务代价和其他非完美信息建模等条件下的UAV辅助通信资源优化。