基于机器学习的直角扣件滑移和扭转性能预测方法
2024-03-04鲍朱杰王斐亮
鲍朱杰, 李 祯, 王斐亮,4, 庞 博, 杨 健
(1. 上海交通大学 海洋工程国家重点实验室,上海 200240; 2. 上海市公共建筑和基础设施数字化运维重点实验室,上海 200240; 3. 广州建筑集团有限公司,广州 510030; 4. 宁波大学 冲击与安全工程教育部重点实验室,浙江 宁波 315211)
目前扣件式钢管模板支架凭借其承载力大、设计灵活、装拆方便、经济效益高等优势在建筑施工领域中有着广泛的应用.然而,由于模板支架架体结构设计不全面和管理缺陷等因素,模板支架倒塌事件频频发生[1],造成严重经济损失、人员伤亡和恶劣的社会影响.
扣件[2]和钢管是模板支架结构重要组成部分,影响模板支架承载性能的因素是多方面的,现有研究通过设计试验[3-6]和数值模拟方法[7-10],验证了扣件增加拧紧力矩对扣件抗滑承载力有着一定的提升,规范要求工程中扣件拧紧力矩介于40~60 N·m[11].同时,相关研究表明钢管厚度、钢管布置形式[6, 12]和实际工程中新旧扣件质量差异[3, 5-6]均会对模板支架承载能力与稳定性产生一定影响.综上所述,在扣件滑移性能和扭转刚度性能设计中应考虑扣件拧紧力矩、钢管公称壁厚、钢管材料属性、扣件铸件弹性模量多种参数的影响.
国内在扣件式钢管模板支架设计方法上参考的技术规范主要包括《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)[11]、《钢管脚手架扣件》(GB 15831—2006)[13]、《建筑施工临时支撑结构技术规范》(JGJ 300—2013)[14]等,《钢管脚手架扣件》中规定扣件铸件材料应按照《可锻铸铁件》(GB/T 9440—2010)[15]设计,模板支架应按照《低压流体输送用焊接钢管》(GB/T 3091—2015)[16]设计.然而,现有规范对扣件式钢管模板支架整体稳定计算以简化计算为主,并未考虑到实际工程中材料、几何尺寸、施工工艺及荷载等方面存在大量不确定因素.由设计标准计算所得到的模板支架失效模式较为单一,而传统的结构力学计算方法相对复杂,且采用简化计算的设计结果准确性难以得到保证.
随着计算机科学技术的发展,机器学习等人工智能技术逐渐应用于解决土木工程各领域的问题,利用机器学习方法可以解决模板支架结构承载性能设计中多变量非线性建模问题.基于神经网络[17-19]、支持向量机(SVM)[20-21]、随机森林(RF)[22]等方法可以识别不同预紧力作用下螺栓连接状态,同时机器学习可用于模板支架结构监测[23]并进行结构安全性分析[24-26],通过监测模板支架在施工过程中的工作状态,给定模板支架所在场地风险水平的安全预测指标,评估模板支架工作情况,建立建筑工地模板支架结构安全状况实时监测系统[27],提出模板支架故障诊断方法[28],确保建筑工地工作区域的安全性.机器学习方法一般需要计算机编程辅助得到预测模型,为得到更为直接的预测模型,有学者[29-30]提出基于基因表达式编程(GEP)开发工程设计直接计算公式.基于机器学习方法可以直接预测直角扣件滑移和扭转性能,同时避免有限元模型直角扣件单元数量多、建模复杂等问题.
针对实际工程中可能出现的扣件预紧力丧失以及复杂的荷载工况模式,本文首先设计直角扣件抗滑移性能和扭转性能试验方案,验证了不同拧紧力矩对扣件抗滑移性能和扭转刚度性能的影响,利用有限元软件建立扣件滑移模型和扭转刚度模型,根据试验结果设计扣件钢管约束条件和加载方式建立模型,同时确定模型输入参数,得到扣件计算模型,并与试验结果相互验证有限元模型的有效性.然后,基于数值模拟方法研究多种设计参数(扣件拧紧力矩、钢管几何参数、扣件铸件材料属性)对扣件承载性能的综合影响,提出模板支架稳定性的加固措施.基于有限元模型和试验结果建立数据库,分别采用随机森林、支持向量机、K最邻近算法(K-NN)3种机器学习算法提出了扣件抗滑移和扭转性能预测模型,从而快速准确进行模板支架安全设计,并对3种开发模型的预测性能进行评估,最后通过基因表达式编程提出模板支架扣件抗滑移和扭转性能的计算公式.
1 直角扣件抗滑移性能和扭转性能试验方案
1.1 试验设计
为探究模板支架螺栓预紧力对扣件节点受力性能的影响,获取不同预紧力条件下扣件节点滑移量,开展直角扣件刚度试验.在试验条件下,采用直角扣件连接竖管和横管,模拟模板支架结构中立杆、横杆连接形式.其中扣件采用KTH330-08可锻铸铁,钢管材料为Q235碳素钢,螺栓为5.6级普通螺栓.结合模板支架结构中扣件连接在实际工程中的应用,拟将抗滑移和扭转性能试件分成5组(S20、S30、S40、S50、S60),每组的扣件拧紧力矩分别为20、30、40、50、60 N·m,从而得到承载性能和失效模式与拧紧力矩之间的关系.
扣件试验方案如图1所示,图中尺寸与试验所需的尺寸保持一致.扣件抗滑移性能试验装置图如图1(a) 所示,横管、竖管长度均为435 mm,在距扣件中心点两侧75 mm处的横管点1处加荷载P/2.选取横管一侧荷载作用点(点1)安装位移计,测量此处的位移Δ1.

图1 扣件试验方案示意图(mm)Fig.1 Schematic diagram of fastener testing program (mm)
进行扭转性能试验中,采用横管为2 100 mm、竖管为435 mm的钢管试件,试验装置如图1(b)所示.试验时在距扣件中心一侧 1 000 mm 处的横管上施加荷载P.选取距扣件中心200 mm 的点2和无荷载端距扣件中心 1 000 mm 的横管点3处安装位移计,测量此处的竖向位移Δ2、Δ3.
1.2 试验装置及加载方案
为研究扣件抗滑移性能和扭转性能,设计试验装置图及加载方案如图2所示.在抗滑移性能试验中,加载点处进行1 kN的预加载,检查试验设备并清零位移测量仪表.清零数显扭力扳手初始数据,设置力矩单位为N·m,添加预置值,扳动手柄平稳施加拧紧力矩以获得不同拧紧力矩状态下的扣件.正式加载后,在扣件两侧的横管上竖向匀速加载,试验装置如图2(a)所示.

图2 扣件试验装置Fig.2 Fastener testing device
在扭转性能试验中,将竖管以铰接形式固定于试验台夹具上,当预加荷载P=20 N时,将测量仪表调整到零点,随后以每100 N为一级加荷,直至加到900 N.在每级荷载作用下记录压力机施加荷载和位移计读数,试验装置如图2(b)所示.
1.3 试验过程及结果分析
直角扣件试验结果如图3所示.对于抗滑移性能试验,从图3(a)中可以看出,加载初期,荷载较小,结构处于弹性范围内.随着荷载增加,钢管位移线性增加.螺栓拧紧力矩为20、30 N·m的构件在小于10 kN荷载作用下发生较大滑移,停止施加荷载,观察发现扣件和钢管并未发生明显的破坏形式.
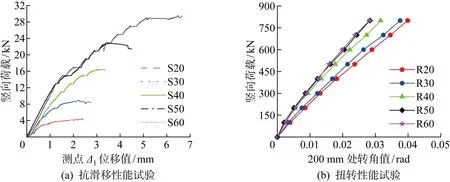
图3 直角扣件试验结果Fig.3 Test results of scaffolding right-angle fastener
随着荷载增加,钢管在荷载作用下的位移增加量逐渐变小,结构进入塑性段.试验结果显示,S40试件在17 kN荷载作用下发生较大滑移,螺栓拧紧力矩为50 N·m的构件在23 kN荷载作用下发生大幅度滑移,螺栓拧紧力矩为60 N·m的构件在 30 kN 荷载作用下发生较大滑移.综上所述,扣件预紧力越大,扣件所能提供的抗滑移能力载越大,抗滑移性能越好.
扭转性能试验如图3(b)所示,结构在受力过程中始终处于弹性范围内.螺栓拧紧力矩 50 N·m相对螺栓拧紧力矩20 N·m刚度提升40%以上.对于扭转性能模型,随着扣件预紧力增加,扣件的刚度可以得到较大的提升.
不同螺栓拧紧力矩作用下的滑移扣件破坏形式基本一致.图4为S40试验组结果的破坏试件,扣件整体无较大变形,扣件盖板内部与钢管接触表面出现油漆脱落现象;在集中荷载作用下,扣件盖板边缘部位产生较大的应力,扣件内侧面产生小变形.

图4 扣件变形图Fig.4 Diagram of fastener deformation
2 数值模拟及参数分析
根据拟定的试验方案建立直角扣件有限元模型,并通过试验结果对有限元建模方式进行验证.利用有限元软件Abaqus对直角扣件抗滑移模型和扭转性能模型进行建模分析,有限元模型中材料参数属性与试验保持一致.模型由扣件、螺栓、钢管组成,扣件采用三维实体模型,螺栓简化成connector单元连接,钢管采用壳单元.钢材应力应变本构关系采用双折线模型,设置接触属性时,法向采用硬接触,切向采用摩擦因数为0.7的罚函数形式,采用实体单元模拟扣件活动铰处螺栓杆,竖管下端采用铰接固定.钢管外径48.5 mm,壁厚3.5 mm.钢材弹性模量为210 GPa,密度为7.85×10-6kg/mm3,泊松比为0.3.
根据《现代机械设计手册》[31],螺栓预紧力计算公式为
fpre=T/(KD)
(1)
式中:fpre为螺栓预紧力;T为螺栓拧紧力矩;K为拧紧力矩系数,通常取0.15;D为螺栓公称直径.螺栓拧紧力矩转化为预紧力的结果如表1所示.
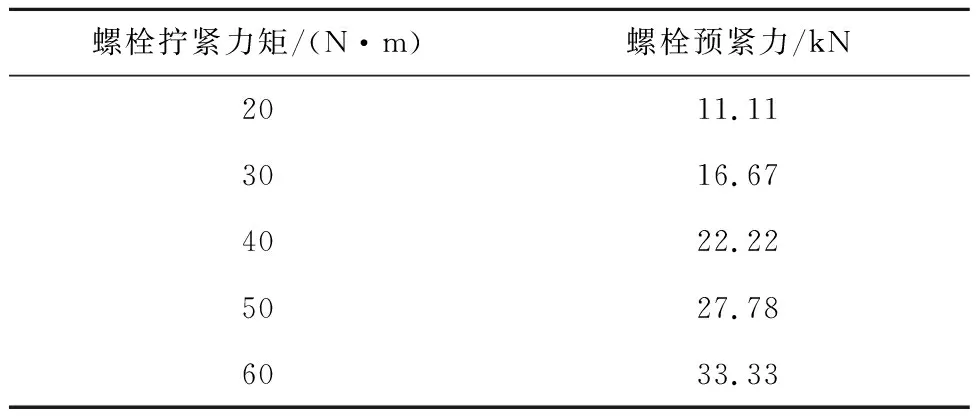
表1 螺栓预紧力Tab.1 Preload force of bolt
划分网格时对扣件板、钢管采取分步切割建模,保证扣件与钢管之间接触位置网格节点对齐,从而形成规则的四边形网格模型.通过网格敏感度分析,确定整个结构网格尺寸为 2 mm.
2.1 抗滑性能有限元模型建立
直角扣件抗滑移有限元模型如图5所示.抗滑性能模型中横管、竖管长度均为435 mm,分别在距离扣件中心75 mm处施加竖向荷载,以S40-M模型组为例,加载至30 kN时,对应的扣件有限元模型图如图5(a)所示.

图5 直角扣件抗滑移有限元模型Fig.5 Finite element model of right-angle fasteners against slippage
图5(b)为抗滑移模型中扣件Mises应力图,从图中可以看出,在竖向荷载作用下,应力较大的位置发生在直角扣件的盖板、底座以及盖板与底座之间连接处.有限元模型中为保证模型计算收敛,钢管与扣件需紧密接触,而试验中由于加工、安装误差等因素,接触面并非紧密接触,二者应力分布有一定差异.整体模型变形图如图5(c)所示.
2.2 抗滑性能有限元模型验证
基于抗滑性能试验结果对上述数值建模方法的准确性进行验证,建立不同预紧力状态下的直角扣件有限元模型.图6给出了5组抗滑移性能模型S20-M、S30-M、S40-M、S50-M、S60-M,分别对应不同螺栓拧紧力矩下测点1竖向位移有限元与试验值对比结果.
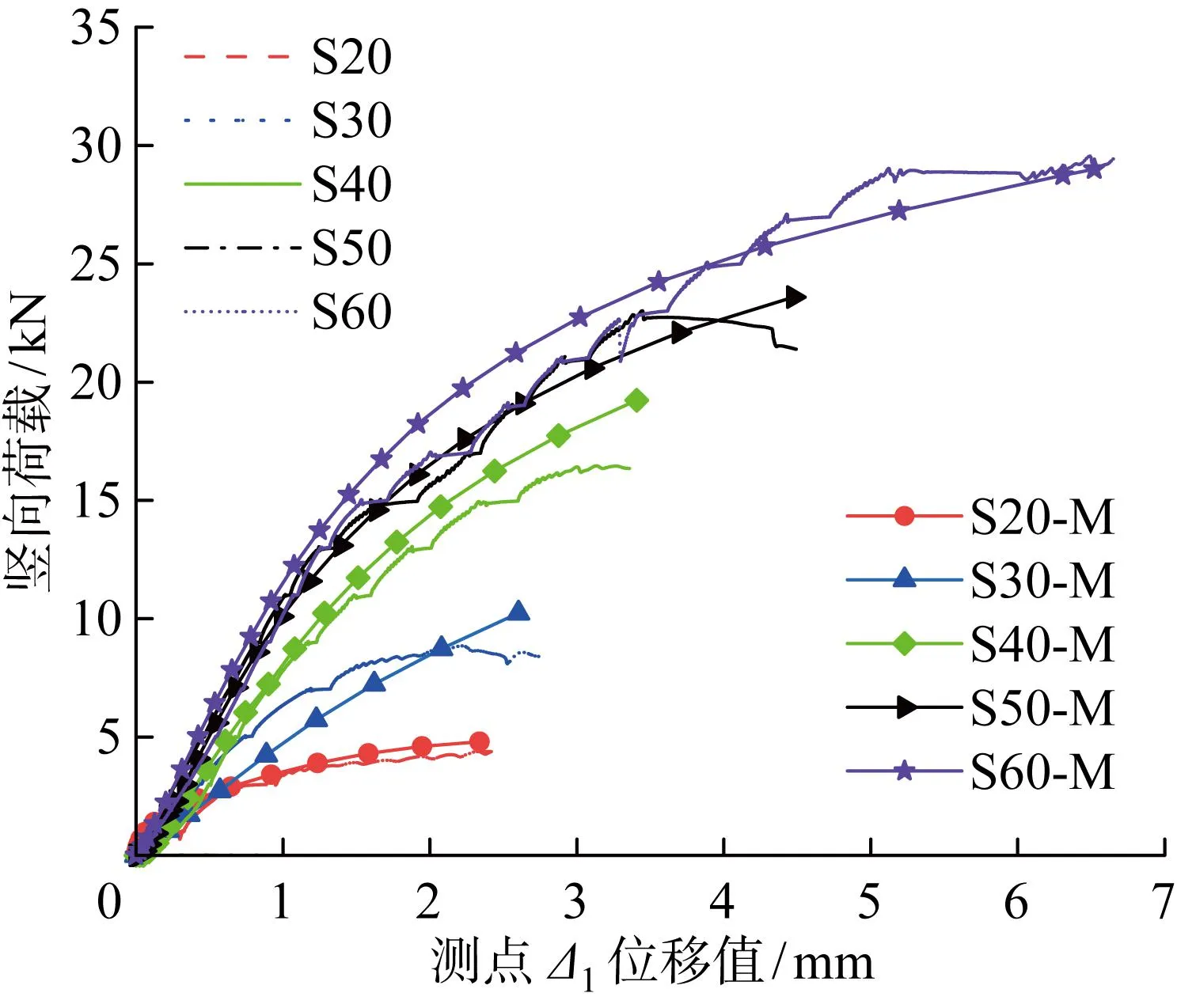
图6 抗滑移性能试验结果和有限元结果对比Fig.6 Comparison of experimental results and finite element results of slip resistance
从各曲线变化趋势上可见,外部荷载较小时,有限元结果和试验结果曲线之间存在一定误差,其误差亦为前述表面应力分布差异所导致.当荷载增加至扣件产生滑移时,有限元和试验结果显示的钢管最大竖向位移量基本相同.综上所述,本文的数值模拟方法可以较好地模拟扣件抗滑移性能.
2.3 扭转性能有限元模型建立
直角扣件扭转有限元模型如图7所示.扭转性能有限元模型与抗滑移性能模型不同之处在于,扭转性能模型中横管长度为2 100 mm,其他设计参数与抗滑性能模型中各参数相同,在距离扣件中心 1 000 mm 处施加竖向荷载,以R40-M模型组为例,加载至 1 000 N 时,扣件有限元模型图如图7(a)所示.

图7 直角扣件扭转有限元模型Fig.7 Torsional finite element model for right-angle fasteners
图7(b)为扭转性能模型Mises应力图,可以看出整个模型在受力过程中始终处于弹性范围内,对应的整体模型变形图如图7(c)所示.
为确定扭转性能试验中刚度对扣件-钢管系统的影响,对所测得位移数据进行处理,距横管中心 1 000 mm 处位移值Δ2按照下式进行转换成转角θ2:
θ2=arctan(Δ2/1 000)
(2)
距横管中心200 mm处位移值Δ3按照下式进行转换成转角θ3:
θ3=arctan(Δ3/200)
(3)
2.4 扭转性能有限元模型验证
基于扭转性能试验结果对上述数值建模方法的准确性进行验证,建立不同预紧力状态下的直角扣件有限元模型.图8给出了5组扭转性能模型R20-M、R30-M、R40-M、R50-M、R60-M中距扣件中心点200 mm处转角的有限元结果与试验实测值对比结果.

图8 扭转性能试验结果与有限元结果对比Fig.8 Comparison of torsional performance test results and finite element results
在扭转性能试验中,构件变形始终处于弹性范围内.从各曲线变化趋势上可见,模拟结果和试验值在整个受力过程中均呈现为线性增长,且两者变化趋势基本一致,本文提出的数值模拟方法可以较好模拟扣件扭转性能.
2.5 参数分析
设定抗滑移和扭转性能有限元模型中初始预紧力为40 N·m、钢管采用Q235材料、扣件弹性模量E=175 GPa、钢管壁厚w=3.6 mm,改变其中一个参数,令其他参数保持不变,进行数值参数分析,研究不同参数节点性能的影响规律,如图9所示.

图9 参数分析Fig.9 Parameter analysis
2.5.1螺栓拧紧力矩影响 考虑20、30、40、50、60 N·m 6种螺栓拧紧力矩工况.图6、图8给出了抗滑性能模型和扭转性能模型结果曲线图.从图中可以看出,R60-M模型扭转刚度是R20-M的1.3倍,改变螺栓拧紧力矩对扣件抗滑移性能和扭转刚度影响较大.工程中应尽量避免因螺栓松动导致的模板支架刚度不足问题.
2.5.2钢管钢材屈服强度影响 对于钢管钢材屈服强度,考虑Q235、Q345、Q450三种材料标号.扣件扭转性能试验始终处于弹性范围内,钢材材料属性对于扣件扭转刚度的影响较小.图9(a)为抗滑移性能模型结果曲线图.从图中可以看出,加载初始阶段(竖向荷载小于12 kN),不同强度构件的荷载位移曲线基本重合,钢材材料对于扣件扭转刚度影响较小,钢材材料标号会影响扣件抗滑移性能.
2.5.3扣件铸件弹性模量影响 扣件铸件材料采用力学性能不低于KTH 330-08牌号的可锻铸铁,铸造工艺、组织结构对于扣件弹性模量影响较大,考虑扣件弹性模量为175、150、125 GPa.图9(b)、图9(c)为抗滑性能模型和扭转性能模型结果曲线图.从扭转性能图中可以看出,弹性模量为175 GPa的扣件刚度相对于125 GPa提升了2倍左右,扣件铸件弹性模量对扣件扭转刚度影响较为明显.扣件铸件生产过程中需要严格保证工艺质量,保证扣件质量强度.
2.5.4钢管壁厚影响 钢管的公称外径和公称壁厚的允许偏差及力学性能应满足规范要求,考虑钢管公称壁厚为3.0、3.4、3.6、3.8 mm 4种常用尺寸.图9(d)、 图9(e)给出了抗滑性能模型和扭转性能模型结果曲线图.从图中可以看出,在抗滑移模型中,相同荷载作用下钢管壁厚为3.0 mm时横管测点位移是壁厚3.6 mm的1.3倍左右;在扭转性能模型中3.6 mm钢管壁厚构件相对于3.0 mm构件扭转刚度提升了10%.钢管壁厚同样会影响模板支架扣件结构性能,在进行模板支架设计时,应确保钢管质量达到规范要求.
3 基于机器学习的抗滑移位移和扭转刚度预测方法
目前大多数模板支架刚度要通过标准规范计算得到预测模型,现有公式和相应的失效模式仅适用于特定条件,然而实际工程中模板支架构件施工质量不同,扣件和钢管尺寸和材料均有不同,综合考虑多参数影响,采用规范公式对每一组扣件计算工作量较大.随着人工智能发展,机器学习技术逐渐应用于解决复杂的工程结构问题,采用机器学习算法模型可以预测不同参数条件下模板支架刚度.本文基于试验数据和有限元模型形成样本数据集,通过随机森林、支持向量机、K最邻近算法3种不同的基于机器学习的分类技术开发模板支架刚度预测模型.
3.1 数据处理
本文基于试验方法和数值模拟方法共收集 1 835 个模板支架扣件测点位移数据.通过改变有限元模型的参数w、钢材屈服强度(fy)、E、螺栓预紧力(fpre)4种参数得到在P作用下的测点竖向位移(d),扣件扭转刚度以横管200 mm处扭转角为评价指标.在收集的数据库中,选择20、30、40、50、60 N·m 6种扣件预紧力矩工况,扣件铸件弹性模量为125、150、175 GPa,钢材材料标号选择Q235、Q345、Q450三种碳素钢,对应钢管公称壁厚为3.0、3.2、3.4、3.6 mm,扣件抗滑移性能要求荷载大小在0~25 kN之间变化.对应不同大小的荷载,扣件抗滑移测点位移最大值为5.235 4 mm,上四分位数为 2.482 2 mm,下四分位数为 0.588 6 mm,所有测点位移平均值为 1.884 0 mm,测点位移中位数为1.273 9 mm;扣件扭转刚度最大值为 6 848.6 N·m/rad,上四分位数为 5 372.8 N·m/rad,下四分位数为 3 365.4 N·m/rad,刚度平均值为 4 624.2 N·m/rad,测点位移中位数为 4 860.4 N·m/rad.通过皮尔逊相关系数分析不同输入参数之间的相关性,计算结果如图10所示.从图中可以看出,非对角线数值结果均小于0.5,各参数间有较强的独立性,相关性较弱.
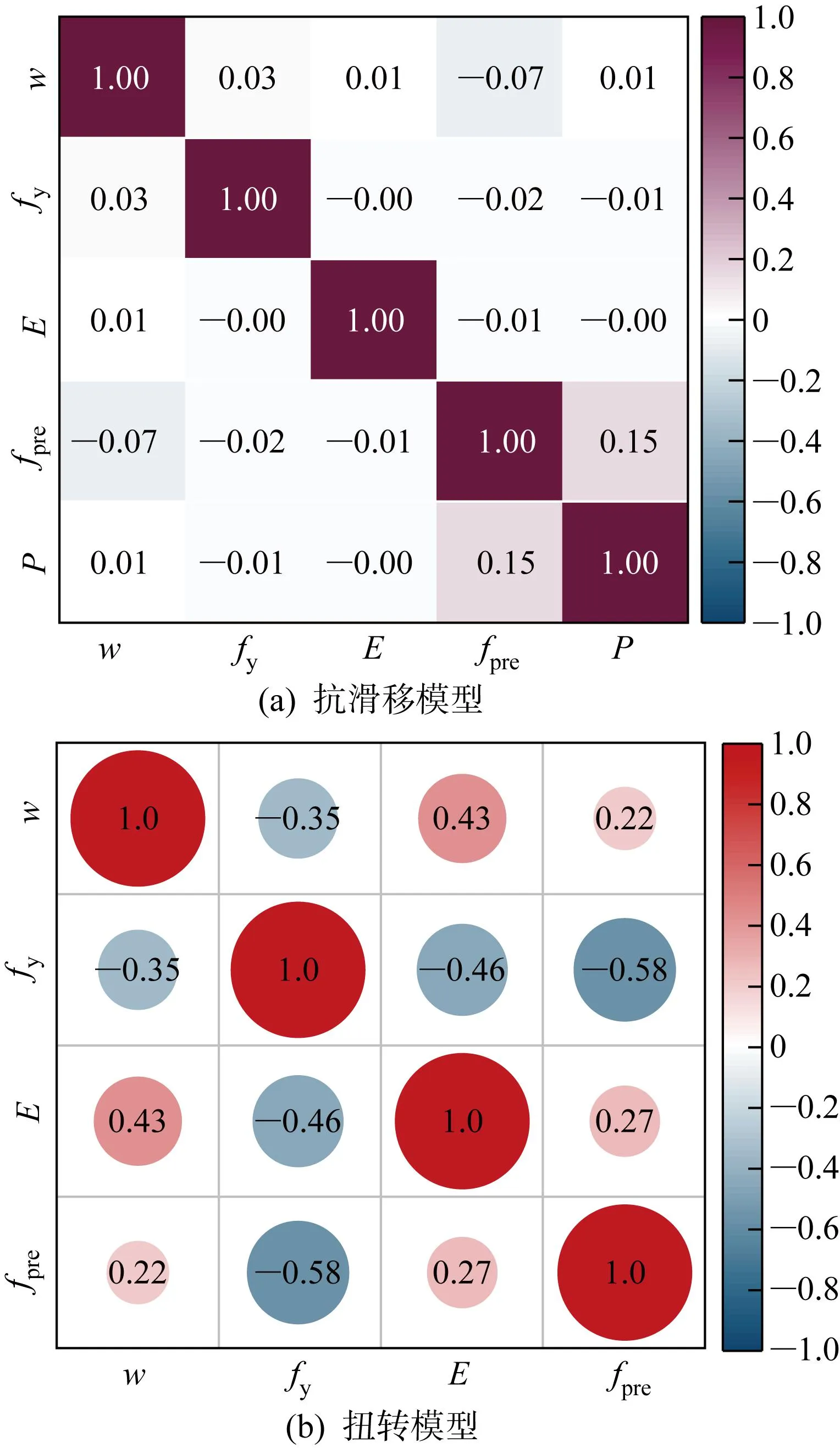
图10 影响扣件性能参数的相关性矩阵Fig.10 Correlation matrix of parameters affecting the performance of fasteners
为避免不同变量分布对模型训练的影响,加快梯度降低求最优解的速度并提高计算精度,对所有数据进行归一化处理.观察发现数据不服从正态分布,使用最大-最小标准化将输入特征缩放至 [0,1] 范围内.进行归一化处理后,将整个数据库随机分为训练集和测试集,其中70%的数据作为训练集,用于训练和优化机器学习模型,选取30%的数据作为测试集,用于测试和评估模型性能.
3.2 模型训练结果评估
基于机器学习算法训练数据集以进行预测模型训练,通过交叉验证调整超参数以减少模型训练过程中过度拟合并进行模型性能优化,采用3折交叉验证方法优化模型超参数.样本数据分为10个子集,9个子集用于训练模型,剩余子集用于测试,在每一步计算中子集分别作为独立测试集,而其他子集充当训练集,保证了均匀采样.表2给出了不同算法超参数的优化值.

表2 3种算法超参数优化值Tab.2 Optimized values of hyperparameters of three algorithms
采用不同的统计指标,相关系数(R2)、均方根误差(RMSE)、平均绝对误差(MAE)、平均值(Mean)和变异系数(COV)评估模型.表3、表4给出了抗滑移性能3种模型的统计指标,从表中可以得出:① RF、SVM模型中R2和平均值约等于1,模型拟合情况良好,对模板支架刚度预测的准确性较高;② 综合训练集和测试集测试结果,抗滑移性能模型和扭转性能模型中,SVM模型的预测性能最好.

表3 滑移模型性能评估Tab.3 Performance evaluation of slip models

表4 扭转模型性能评估Tab.4 Performance evaluation of torsional model
3.3 基因表达式编程(GEP)
为了获得显式的预测结果,采用基因表达式编程开发计算公式完成对扣件抗滑移性能和扭转刚度性能的预测,以方便工程人员的实际使用.GEP是由Ferreira[32]提出的一种基于生物基因结构和功能发明的新型自适应演化算法,实质是用广义的层次化计算机程序描绘问题.结合上述机器学习方法给出的不同算法模型性能评价结果,采用GEP对扣件抗滑移性能和扭转性能进行定量分析.
3.3.1模型建立 采用扣件抗滑移性能试验中钢管壁厚、钢管材料属性、扣件弹性模量、螺栓预紧力4种重要参数和集中荷载作为输入变量,取横管上距扣件中心75 mm处测点位移进行预测分析,即d=f(w,fy,E,fpre,P).扣件扭转刚度与钢管壁厚、钢管材料属性、扣件弹性模量、螺栓预紧力有关,即k=f(w,fy,E,fpre).GEP算法模型中涉及的重要参数如表5所示.
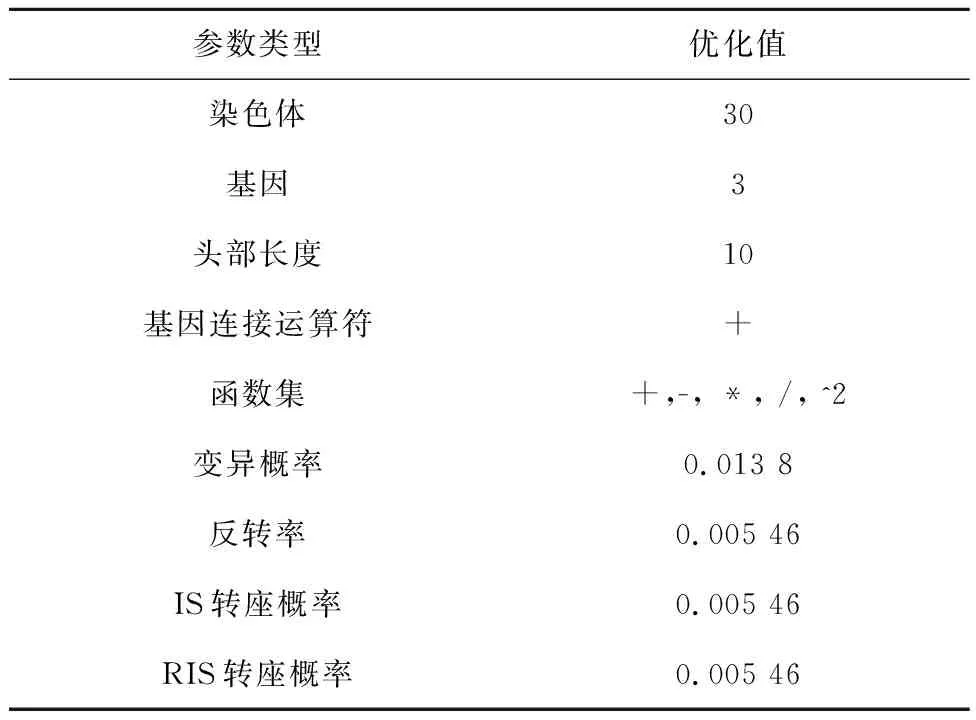
表5 GEP参数优化值Tab.5 Optimized values of GEP parameters
3.3.2模型结果 图11给出了GEP模型中扣件抗滑移测点位移和扭转刚度实际值和预测值, 抗滑移性能模型中训练和测试阶段模型的相关系数R2为0.91,扭转性能模型训练和测试阶段模型的相关系数R2为0.96.因此,采用GEP模型预测扣件抗滑移测点位移和扭转刚度具有较好的精确性.
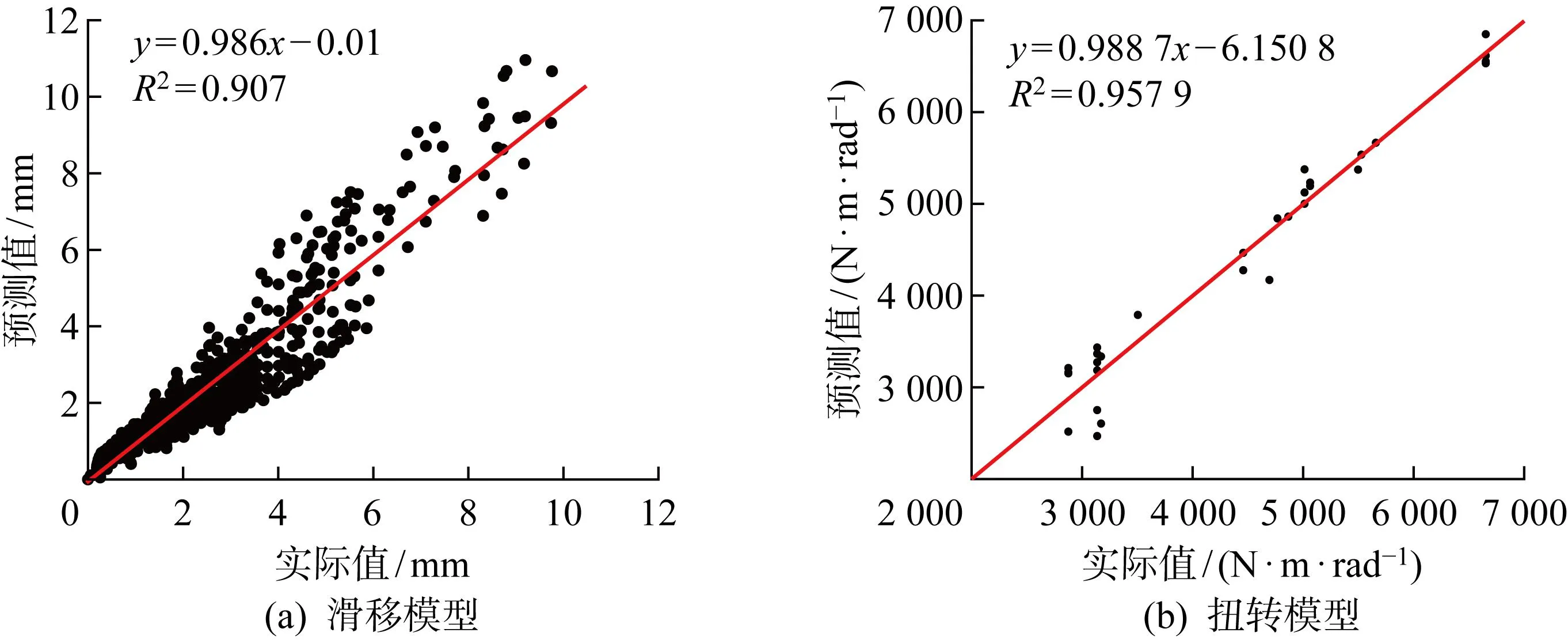
图11 实际值与预测值对比Fig.11 Comparison of actual and predicted values
根据现有模型的输入参数组合形式及试验数据库的皮尔逊相关性分析结果提出的扣件抗滑移位移和扭转性能刚度预测模型具有较高的精度,得到的公式能对扣件抗滑移性能和扭转性能刚度进行准确预测.预测扣件抗滑移测点位移d和扭转刚度k的表达式如下:
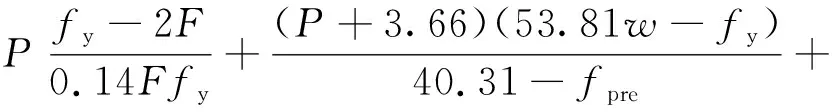
(4)
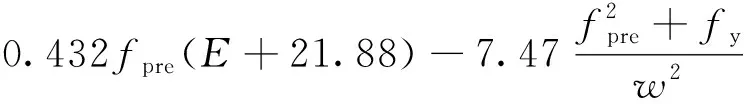
(5)
4 结论
(1) 模板支架扣件滑移试验结果表明,螺栓拧紧力矩对扣件滑移量影响较大,螺栓拧紧力矩为20、30 N·m的扣件均在10 kN以下产生大幅度滑移,螺栓预紧力为50、60 N·m提高了2倍以上的抗滑性能;扣件盖板边缘区域为模板支架结构受力薄弱部分,模板支架结构设计应加强该区域的受力分析.
(2) 本文采用的混合数值模拟方法可以较好反映扣件承载力试验中变形情况,二者拟合情况较好.钢材强度高的材料对于扣件抗滑性能有一定的提升,而Q450钢材相对于Q345钢材的抗滑性能提升较小,采用Q345钢材可满足抗滑性能基本要求;扣件弹性模量对节点的刚性影响较大,对扣件扭转性能影响较为明显;钢管公称壁厚较小时,对于整个扣件结构的削弱影响较大,钢管壁厚每减少4 mm,抗滑性能约降低20%.
(3) 本文提出3种基于机器学习算法预测模型,其中RF模型和SVM模型均能较好预测扣件抗滑性能,相关系数分别为0.99、0.98,且SVM模型的预测效果最好,均方根误差为0.65.根据GEP模型得到扣件抗滑移性能中测点位移和扭转性能刚度表达式,模型相关系数分别为0.91和0.96,对扣件抗滑移和扭转性能模型刚度预测较为精确.
