基于深度学习的螺旋桨水动力性能快速预报方法
2024-03-04胡安康侯立勋
高 楠, 胡安康, 侯立勋, 常 欣
(大连海事大学 船舶与海洋工程学院,辽宁 大连 116026)
螺旋桨的敞水水动力性能是校核优化设计和验证理论方法的重要依据.目前,敞水性能的获取方式主要有3类:敞水试验、势流理论法和基于黏性流体理论的计算流体力学(Computational Fluid Dynamics, CFD)法.
敞水试验是最传统的获取敞水性能的方法,也是研究螺旋桨水动力性能的重要方法,但试验成本偏高且不具备快速预报的能力.
势流理论法以3种为主:升力线法、升力面法、面元法.升力线法在涉及螺旋桨侧斜和纵倾问题时局限性很大;升力面法不能直接预报桨叶导边区域的压力分布,对空泡性能的预报精度较低;面元法未考虑流体自身黏性,无法解决与流体黏性相关的问题.
CFD法能够避免敞水试验高费用的缺点,并考虑了流体黏性,可以捕捉大量物理信息,在螺旋桨性能研究领域收到众多学者的应用,但计算周期长达数小时,不能满足实时预报的要求.
因此,开发一种基于桨叶几何参数进行快速预报不同类型螺旋桨敞水性能的方法对螺旋桨的优化设计和理论校核有重要意义.机器学习理论的发展为螺旋桨性能预报提供了新思路,例如Choi 等[1]利用深度强化学习预测船尾螺旋桨轴形变,Bakhtiari 等[2]通过构建一个3层的神经网络模型对某小螺距比的螺旋桨进行快速预报, Shora 等[3]基于反向传播(BP)神经网络预报螺旋桨敞水性能与空泡性能,王超等[4]基于椭圆基神经网络与遗传算法开展KP505桨的优化设计与参数分析,Xue 等[5]基于双隐藏层的BP神经网络与遗传算法对P4382桨进行优化设计,均显著提高了螺旋桨性能,还有些学者基于卷积神经网络进行螺旋桨辐射噪声预测[6-8],取得了不错的效果.总之,在对某一桨型进行优化设计或性能预报方面,机器学习的精度与快速性已经获得众多学者的认可与应用,但模型缺乏普适性,仅对特定桨有较高的精度,若预测其余桨型则需重新进行模型训练、调整模型的超参数,将耗费大量人力、时间成本,快速性的优势不复存在,这极大限制了其在工程实践中的应用范围.
缺乏普适性的原因在于目前的研究大多只采用单一结构的神经网络:BP神经网络、椭圆基神经网络或卷积神经网络,模型缺乏同时处理多个维度不同的螺旋桨几何参数的能力,输入向量缺乏足够表征桨叶形状的能力,这正是实现预测不同类型螺旋桨水动力性能的关键技术,因此目前只能实现对特定桨的快速预报.传统机器学习模型为避免梯度爆炸或消失问题导致模型收敛效果不佳,只能采用少量的隐藏层,并在每层中设置大量的隐藏单元,导致模型参数过多,收敛速度较慢,但对复杂数据的拟合效果并不理想.且当前研究仅凭随机产生的初始权重与阈值进行模型训练,因此模型存在陷入局部最优的问题,导致预测精度与CFD法相比存在差距,在实践中存在较大的局限性.
为实现螺旋桨水动力性能的快速、精确预报,提出一种基于改进的残差神经网络的螺旋桨水动力性能预报模型,通过残差连接方式彻底解决传统神经网络随深度增加导致的梯度消失或爆炸问题,从而大幅增加模型深度,采用多分支并联的 Inception 结构增加了模型宽度,可以同时从多个不同尺度提取数据特征,实现实时准确预报不同类型螺旋桨水动力性能. 为对模型的初始权重与阈值进行优化,避免模型训练陷入局部最优,进一步提高模型的预测性能,提出一种改进的天牛群搜索(Improved Beetle Swarm Antennae Search, IBSAS)算法,在每次更新全局与个体的历史最优解时,基于Metropolis准则进行二次判定,解决陷入局部最优的问题,每次迭代的搜索范围能够通过自适应因子根据当前搜索结果自行调节,避免错过最优解,最终为螺旋桨的设计工作提供一套高效、可靠的水动力性能预报工具.
1 方法原理与实验
1.1 改进的残差神经网络模型
传统机器学习模型的梯度随深度增加以累乘的方式递增,这极大限制了模型的纵向深度,使其对复杂的高维度数据的拟合能力欠佳,因此并不适用于预测不同类型螺旋桨的水动力性能.因此本文提出一种改进的基于Inception结构与深度残差神经网络(Deep Residual Network, DRN)相结合的深度残差网络(Improved Deep Residual Network, IDRN)模型,模型中每个模块的结构如图1所示.图中:虚线部分为残差连接方式;x为模型输入;F(x)为残差映射映射.模型误差的反向传播如下:
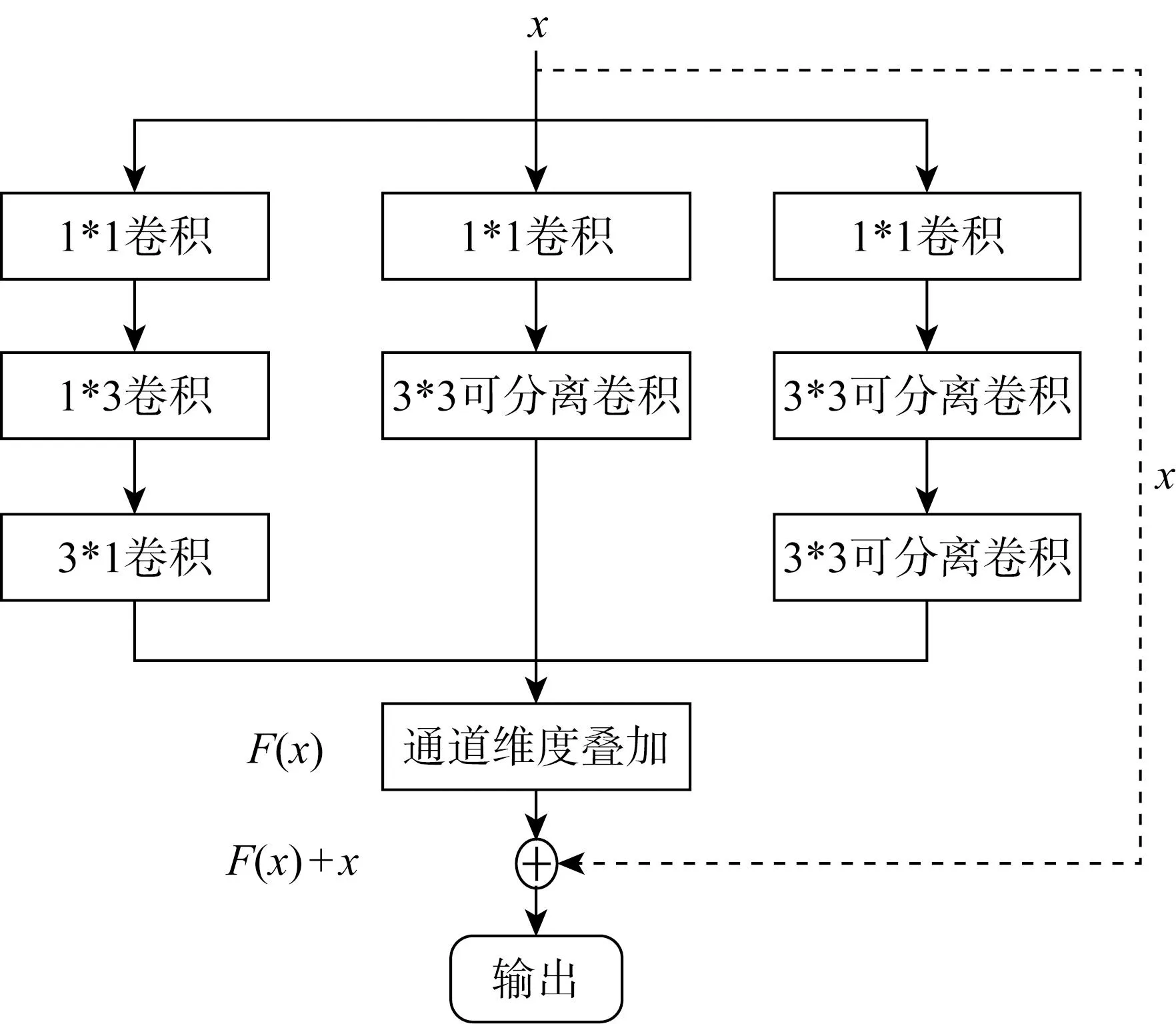
图1 改进的Inception-DRN结构Fig.1 Structure of the improved Inception-DRN
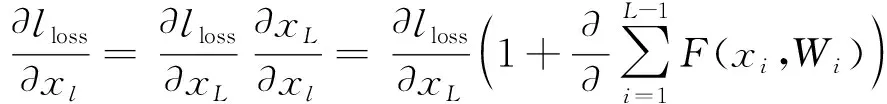
(1)
式中:lloss为损失函数值;F为输入与输出间的映射;xl为残差单元的输入;l为残差单元的索引值;L为比l更深的残差单元层数;W为权重.
模型梯度随深度增加以累加的方式递增,彻底解决深度增加导致的梯度消失或梯度爆炸的问题,使深度残差神经网络比基于单向连接的神经网络具备更深的纵向深度,大幅提高了模型的非线性拟合能力.每个模块由3个具有不同尺寸卷积层的分支结构并联而成,同时拓展了神经网络的宽度与深度.每个分支的第1层均使用1*1的卷积核进行降维,减少模型参数,后续每个不同尺寸的卷积核可以捕捉输入数据在不同尺度上的特征,虚线部分为用于调整通道维度的卷积运算.
传统神经网络随深度或宽度增加会导致网络中待学习参数过多,使模型收敛较慢,改进的Inception模块用连续的深度可分离卷积核替换常用的大尺寸卷积核,不降低计算精度并减少计算参数为传统卷积的1/5,缓解了 IDRN模型因深度与宽度的大幅增加导致的参数爆炸问题.
模型具体结构如图2所示.图中:x1,x2,…,xq为输入向量;KT和KQ分别为推力系数和转矩系数.模型整体由两部分构成:一部分由多个全连接层构成;另一部分由50个如图1所示的改进 Inception-DRN单元构成,二者分别用于提取FS1与FS2中的数据特征(FS1为一维标量,FS2为二维向量),使模型具备同时提取不同维度几何参数特征的能力,能够更精确地拟合螺旋桨桨叶形状与其水动力性能间的映射关系.

图2 深度学习预报模型结构Fig.2 Prediction model based on deep learning
模型的优化器为自适应矩估计(Adaptive Moment Estimation, Adam)算法, 以均方误差(Mean Square Error, MSE)为损失函数,其定义如下:
(2)
式中:yi为样本真实值;f(xi)为模型预测值;n为样本个数.
使用Morlet小波函数作为神经元的激活函数,其定义如下:
(3)
式中:A为重构时的归一化常数,本文A=1;ζ为神经元的输入值.
1.2 改进的天牛须搜索算法
天牛须搜索(Beetle Antennae Search, BAS)算法是一种仿生优化算法,搜索方向完全随机,收敛速度较慢,每次迭代的步长固定,可能会错过全局最优解或陷入局部最优.因此本文提出改进的天牛须搜索(Improved Beetle Antennae Search, IBAS)算法,利用k个智能体进行寻优,引入自适应步长调节因子c,其定义如下:
(4)
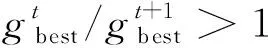
(5)
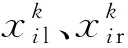
(6)
式中:fil与fir分别为左须与右须适应度值.假设当前的全局历史最优适应度值为fbest,仅当fbest更新时,全局历史最佳位置xgbest才会更新,但每轮迭代中的全局最优适应度仍会被记录,便于搜索步长根据式(6)进行自适应调节,个体的历史最佳适应度值与历史最佳位置的更新也同理.

Metropolis准则的作用如图3所示.
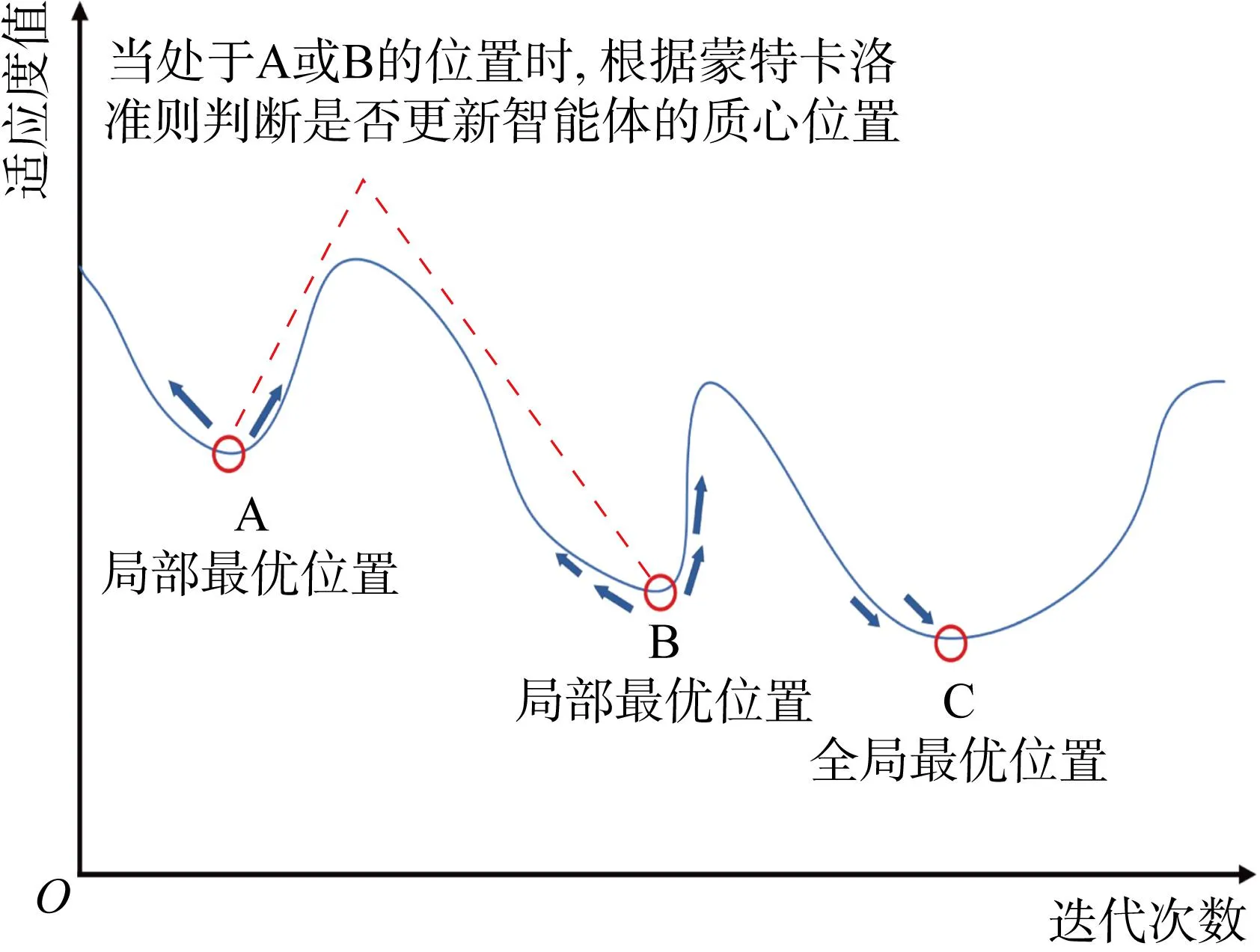
图3 Metropolis准则解决局部最优问题Fig.3 Metropolis criterion for solving local optimal problems
改进后的BAS算法流程如图4所示.图中:e为一个[0,1]的随机数.
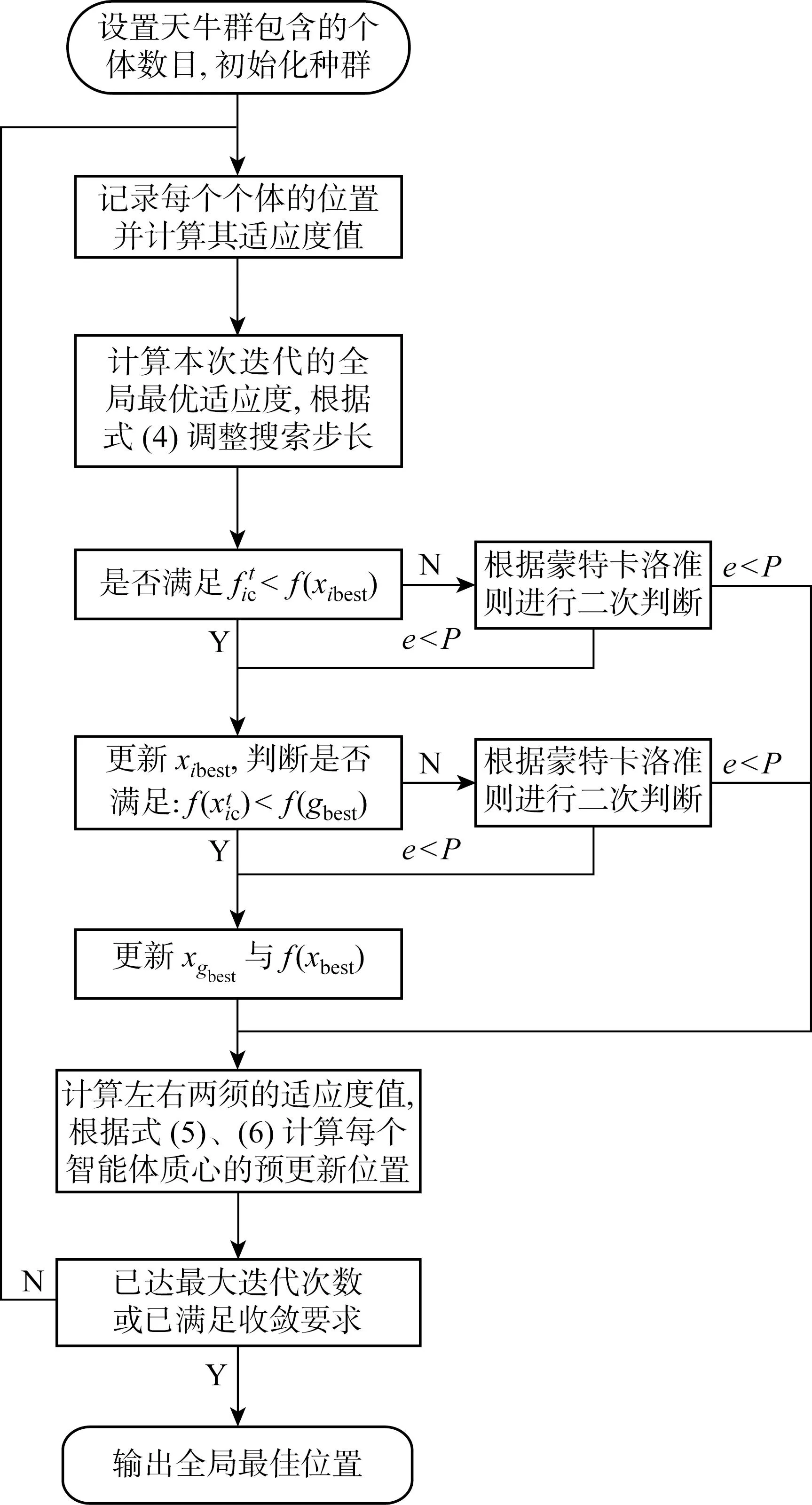
图4 改进的BAS算法流程图Fig.4 Process of the improved BAS algorithm
1.3 确定输入与输出变量
本文的输入变量input由FS1、FS2构成,输出变量output由敞水水动力性能(OPS)构成.FS1包含关于螺旋桨尺寸、工况的变量;FS2包含每个标准桨的11个桨叶剖面的几何特征,均为二维向量;OPS中涵盖了每个螺旋桨在J=0.1到J=1.0工况下的KT与KQ,数据集如表1所示.
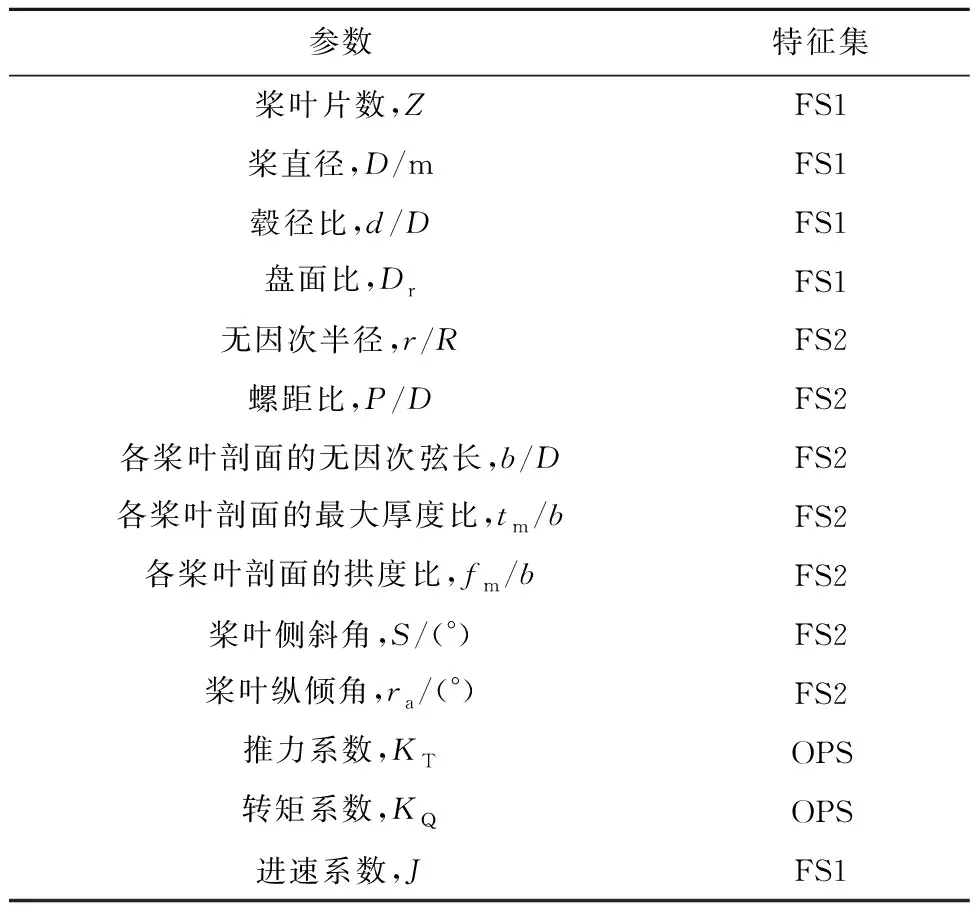
表1 桨叶几何参数及其敞定水水动力性能义Tab.1 Definition of blade geometrical parameters and hydrodynamic performance
为预测尽量多类型的螺旋桨的敞水性能,选取了常见的18种桨型(有无侧斜与纵倾、定螺距与变螺距、三叶桨至五叶桨),涵盖了各类型船舶常用的螺旋桨类型,满足不同船舶的性能需求,因为当前用于大型船舶的螺旋桨性能研究是该领域的前沿课题,所以数据集中用于大型船舶的螺旋桨占总数的比例约为61.1%,这使预报模型具备更强的工程实践意义.数据集详细数据如表2所示,相关几何参数与试验值见文献[9-33].表中:P/D(0.7R)为0.7R处的螺距比.以严格分割方式即训练集与测试集间无交集,将数据集分为训练集与测试集,训练集包含的桨型较多.

表2 数据集内的螺旋桨及其主要参数Tab.2 Propellers and their main parameters in the data set
2 试验与分析
首先基于8种标准测试函数开展基于改进的天牛群搜索算法的优化性能分析试验,并与几种传统优化算法进行对比,验证该算法的有效性.其次对比IDRN模型与其他深度学习模型对本文数据集的训练效果,并利用IBSAS算法对模型的初始权重与阈值进行优化,最后选择数据集之外的螺旋桨检验优化后的IDRN的性能.
测试函数及其取值区间如表3所示,f1~f4
为单峰函数,f5~f8为多峰函数.选取BAS、天牛群搜索 (Beetle Swarm Antennae Search, BSAS)算法、粒子群搜索(Particle Swarm Optimization, PSO)算法、模拟退火(Simulated Annealing, SA)算法作为对比算法,为确保算法的收敛性,所有算法均设置5 000次迭代,搜索空间的维度均为30,且在每个函数上的初始位置均由同一随机种子生成,避免因随机初始化带来的性能差异,PSO、BSAS、IBSAS的种群规模均为50.
2.1 基于单峰函数的性能评估
5种算法在f1~f44个单峰测试函数上的适应度收敛曲线如图5所示.
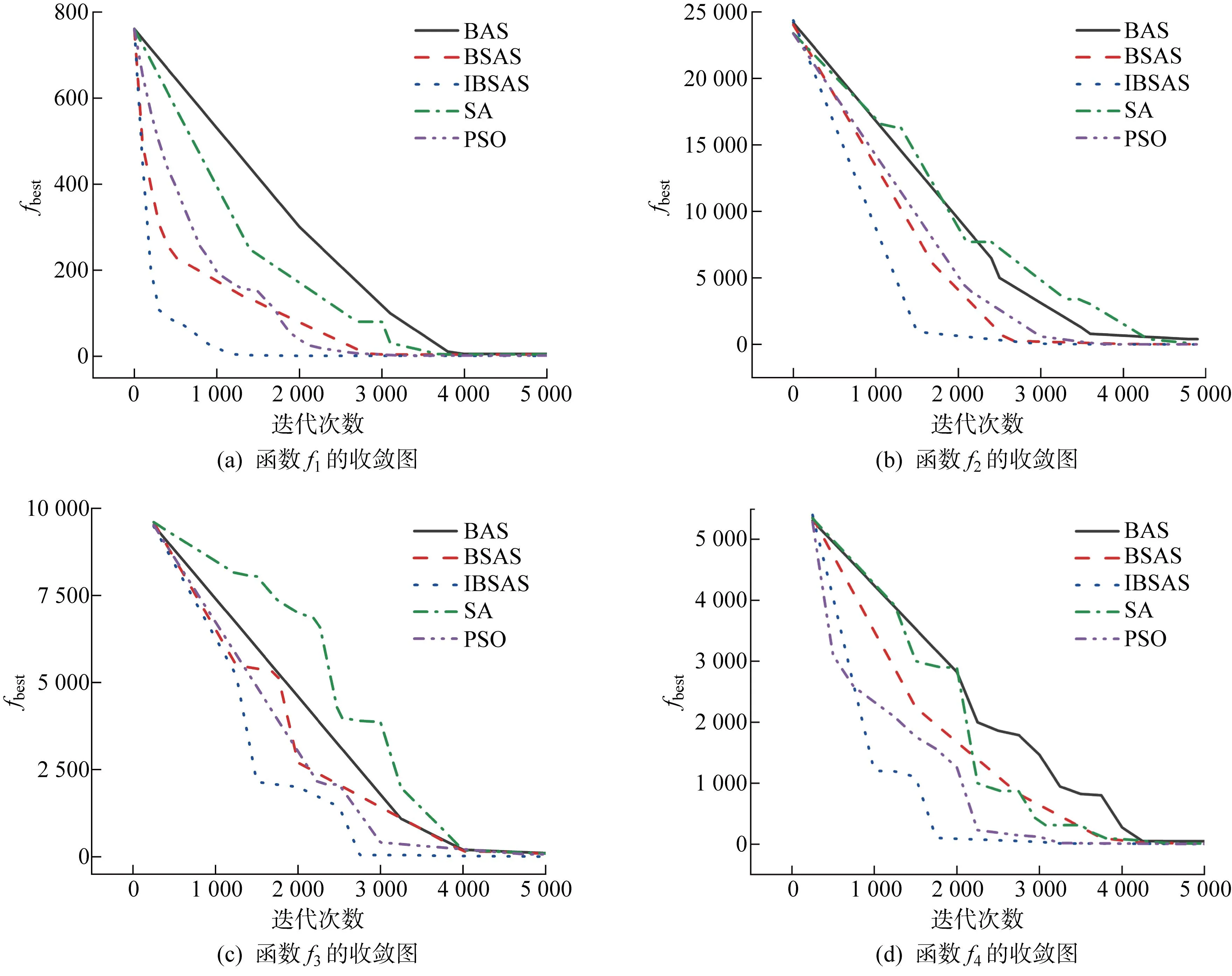
图5 5种算法在单峰函数的收敛曲线Fig.5 Convergence curves of five algorithms in unimodal functions
从总体来看,IBSAS算法在单峰函数上的性能表现明显优于其余4种算法.在f1~f4上,IBSAS 算法分别历时 1 249、1 748、2 736、1 826 次迭代时寻到最优值,其余3种算法最快则需 2 437、2 583、3 174、3 195 次迭代,证明IBSAS搜索效率显著高于传统算法;寻优过程中,IBSAS的收敛速度经历多次变化,这是因为步长调节因子在自适应的调节搜索步长,平衡算法的全局搜索能力与局部精确勘探能力,迭代初期快速接近最优解,当接近最优位置时则急速减小每次迭代的搜索范围,避免错过最优解.
2.2 基于多峰函数的性能评估
5种算法在多峰函数f5~f8上的适应度收敛曲线如图6所示.
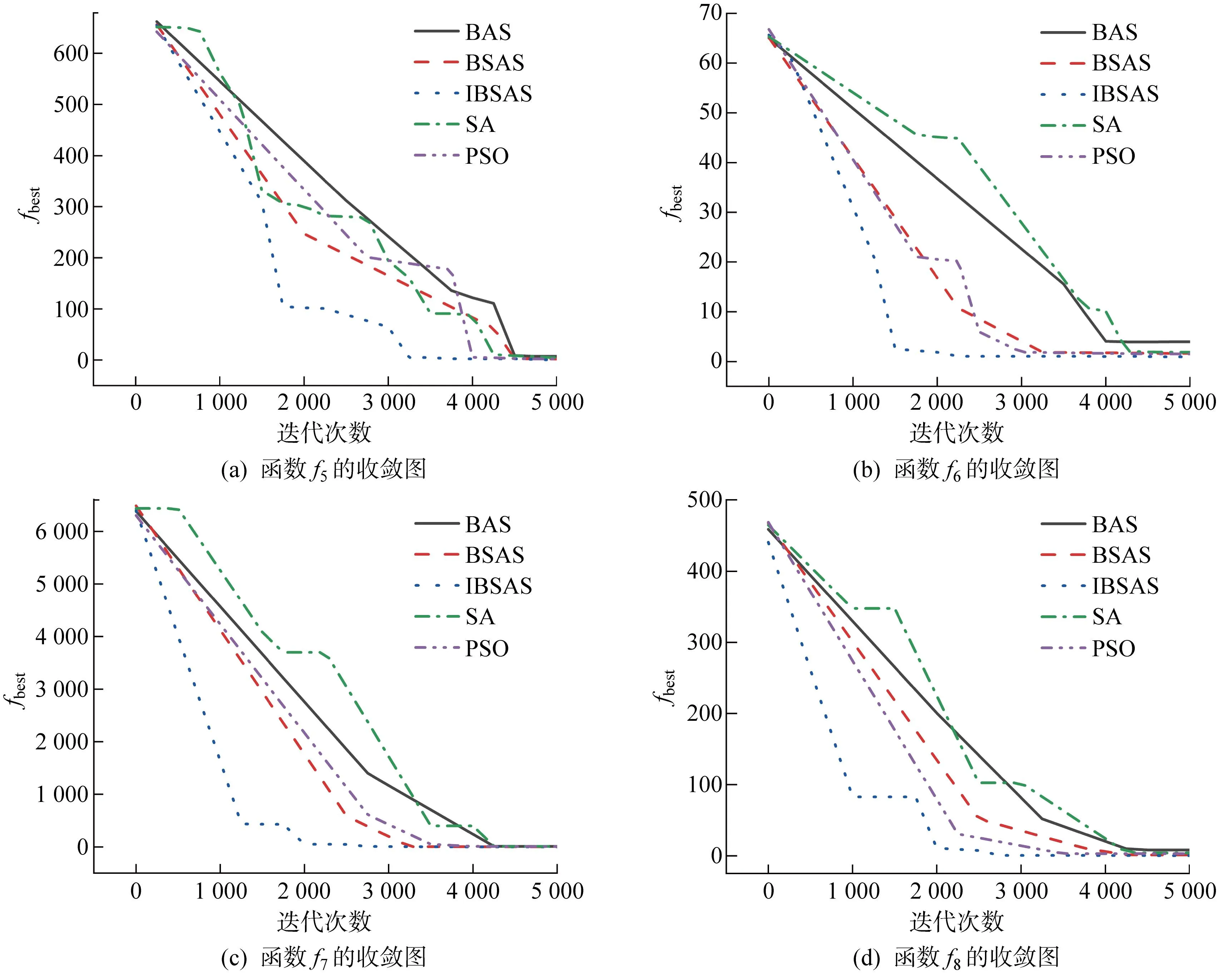
图6 5种算法在多峰函数的收敛曲线Fig.6 Convergence curves of five algorithms in multimodal functions
IBSAS算法在多峰函数上的寻优过程基本相同:初期收敛速度极快,然后进入一段停滞期,最后以逐渐下降的速度结束搜索.因为多峰函数存在多个局部最优解,IBSAS算法在搜索过程中陷入局部最优的频率明显高于单峰函数试验,停滞期也更长,但在个体质心位置迭代时结合Metropolis准则进行二次判定,使其在一定次数迭代后成功脱离局部最优位置.在f5、f6、f7函数上,IBSAS算法寻优速度远高于其余4种算法,分别历时 3 285、2 643、2 375 次迭代,其余4种算法中最快则需 4 087、3 471、3 657 次迭代,分别提高了19.62%、23.85%、35.06%;在f8函数上的性能表现是两者差距最小的一次,IBSAS算法历时 2 946 次迭代,其余算法中最快完成搜索的PSO算法则需 3 679 次迭代.总的来说,IBSAS算法在针对多峰函数上的优化效率全面优于传统算法.
2.3 基于IBSAS算法的深度学习模型优化
随机产生的初始权重与阈值极可能导致IDRN模型陷入局部最优问题,导致最终的收敛结果不理想.为解决这一问题,采用IBSAS算法对神经网络的初始权重与阈值进行优化,优化流程如图7所示.

图7 IBSAS算法优化IDRN流程图Fig.7 Optimization of IDRN by IBSAS
对比BAS、PSO、SA、BSAS算法对IDRN的优化效果,所有算法均设置6 000次迭代,每种算法在优化过程中的适应度收敛曲线如图8所示.
IBSAS、PSO、BSAS算法的种群规模均为50,IBSAS、BSAS、BAS算法的初始步长均为0.35,BSAS 的步长衰减系数均为0.95,每种算法均由同一随机种子完成初始化,IDRN模型中总计12 778 516 个初始权重与阈值待优化.
IDRN的参数数量远远超过8个测试函数的参数个数,输入与输出之间的映射关系也更复杂,因此算法间的优化效率差异愈发明显.从结果来看,IBSAS、BAS、BSAS、SA、PSO的fbest收敛值分别为0.030 49、 0.095 03、0.085 02、0.106 37、0.084 31,可见 IBSAS的优化效果远好于其余4种算法.优化过程中,IBSAS算法经历了两次约400次迭代的停滞,瓶颈期后收敛速度略有下降,这一方面是因为优化过程中IBSAS算法两次陷入局部最优,但都成功脱离;另一方面,收敛速度的下降是由步长衰减因子根据当前的优化进程自适应地调节搜索范围,避免错过全局最优解.其余4种算法的收敛值均在[0.084 3, 0.107 0]区间内,说明算法在fbest下降至这一区间时落入局部最优陷阱或因搜索步长过大而错过全局最优解,相比之下,IBSAS算法很好地弥补了这些缺陷.
图9给出了经以上5种算法优化后的IDRN模型与未优化的IDRN模型分别在训练集与测试集上的性能表现,训练轮次均为 3 000 次,学习率均为0.001.

图9 优化与未优化模型训练与测试过程的对照Fig.9 Comparison of training and testing process of optimized and unoptimized models
5种算法中,IDRN模型经IBSAS算法优化后的性能提升最为显著,在训练集上,IBSAS算法将模型的E值降低至仅为 0.008 44,而其余算法中优化效果最好的BSAS算法仅将E值降至 0.098 89,模型的收敛速度也略有提高;就模型测试而言,IBSAS 算法将E值降至 0.009 8,其余算法中优化效果最佳的BSAS算法仅将E值降至 0.131 92, IBSAS-IDRN 的收敛速度也显著高于其余模型.因数据集中螺旋桨的几何形状差异较大,模型的E值在收敛过程中处于波动状态,但IBSAS-IDRN的E值振幅远小于其余模型,说明IBSAS-IDRN的性能更加稳定.
2.4 IDRN模型性能试验
为进一步对比IDRN模型的性能,分别建立了基于深度卷积神经网络(DCNN)的模型与传统深度残差神经网络(DRN)模型进行对照试验,采用网格搜索法确定模型的超参数,应用IBSAS算法对其初始权重与阈值进行优化,因此,DCNN与DRN的结构针对本文数据集已调至最优,与IDRN对比时,可以排除非模型结构的影响,训练轮次为 3 000.IDRN与DCNN、DRN在训练与测试过程上的性能表现如图10和表4所示.表中:Etrain和Etest分别为模型训练与测试中的MSE收敛值.
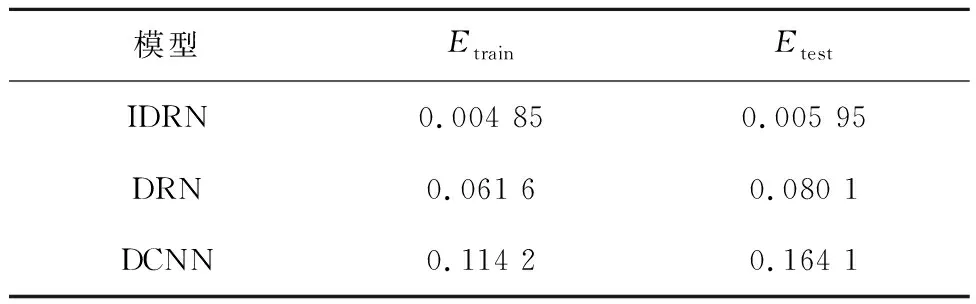
表4 IDRN、DRN、DCNN在训练与测试中的MSE收敛值Tab.4 Convergence value of MSE of IDRN, DRN, and DCNN in the training and test
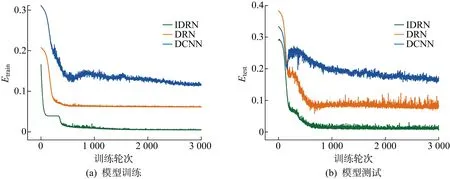
图10 IDRN、DRN、DCNN的性能对比Fig.10 Performance comparison of IDRN, DRN, and DCNN
由图10可知,IDRN在模型训练与测试时的性能表现明显优于DRN与DCNN:IDRN的收敛速度略快于其余模型,在训练与测试过程中DCNN的E值出现大幅的波动,而IDRN仅在初期存在小幅波动.由表4可知,IDRN的Etrain与Etest分别为 0.004 85 与 0.005 95,远低于DRN与DCNN,这说明IDRN模型具备更强的拟合能力,一方面是因为残差连接方式使模型的深度较DCNN有了大幅提高,另一方面是因为并行计算使模型可以从不同尺度提取数据特征.
IDRN模型的Etrain与Etest之间的差值也远小于DRN和DCNN,这表明IDRN在不同数据上的性能表现差异不大,其过拟合程度远低于DRN与 DCNN.
为检验IDRN对数据集之外的螺旋桨敞水水动力性能的预测能力,选取数据集之外的已公开几何参数的标准桨:KP505与B4-70为例[33-34],KP505桨与数据集中的任何桨均不属于同一系列,而B4-70桨与B4-55、B4-40桨同属于B型螺旋桨,全面考察模型的普适性与有效性、可行性.两者的几何参数如表5所示.表中:S(0.7R)、b/D(0.7R)、tm/b(0.7R)和fm/b(0.7R)分别为0.7R处的侧斜角、无因次弦长、最大厚度比与拱度比.用经IBSAS算法优化后的IDRN预测该桨的敞水性能,并与CFD法[34-35]、BP神经网络以及敞水试验值[34,36]对比.

表5 KP505与B4-70的主要几何参数 Tab.5 Main geometrical parameters of KP505 and B4-70
选择BP神经网络模型(BP Model, BPM)进行对照试验是因为它在预测特定桨的敞水性能方面已获得众多学者的应用,BPM的超参数由网格搜索法确定.利用IBSAS算法对初始权重与阈值进行优化,并基于KP505与B4-70的敞水试验值进行模型训练.
IDRN与BPM、CFD对B4-70的敞水性能预测值及其敞水试验值的对比如图11所示,IDRN预测的KT与10KQ的相对误差分布如图12所示.
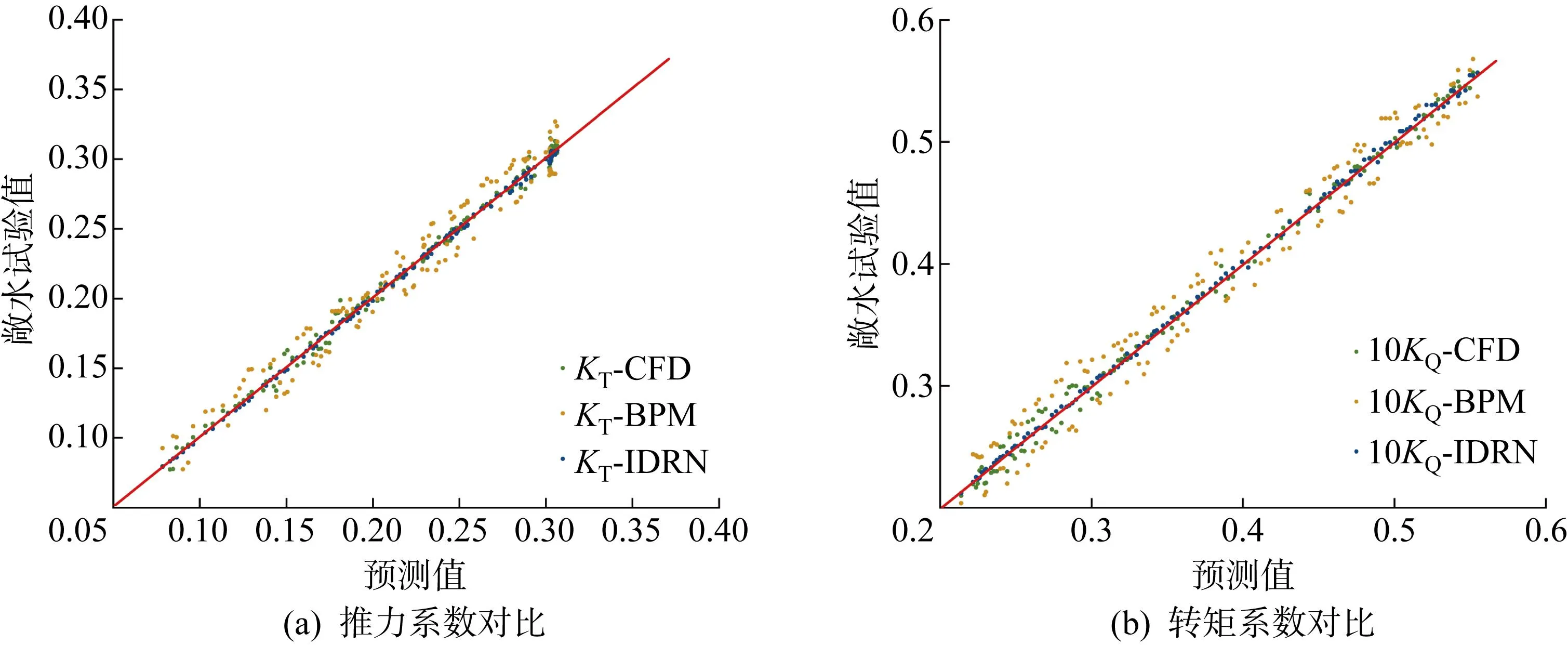
图11 IDRN、CFD法、BPM对B4-70的预测值与其敞水试验值的对比Fig.11 Comparison of the predicted values of B4-70 by IDRN, CFD, and BPM with the measured value of open water test

图12 IDRN对B4-70的预测值的相对误差分布Fig.12 Distribution of relative error of the value predicted of B4-70 by IDRN
图11中,选取进速系数J在区间[0.1, 0.9]内共128个工况下对应的KT与10KQ值,红线为完美回归线.B4-70与数据集中的B4-40和B4-55同属于B型螺旋桨,本实验旨在考察模型与数据集的有效性,结果表明,IDRN的平均预测精度显著高于BPM,所有工况下的预测值与试验值吻合度极高,预测值的最大相对误差仅为1.74%,在KT与10KQ的预测值中均仅有2个工况的相对误差大于1.5%.由图12可知,KT与10KQ的相对误差主要集中在0.5%~1.0%,这表明IDRN的预测精度与稳定性均远好于BPM;CFD的预测结果与试验值的吻合度较高,最大相对误差仅为3.17%,在KT与10KQ的预测值中分别仅有2个和3个工况的相对误差超过3%,可见,对于数据集中的系列螺旋桨,即使该系列中某螺旋桨不在数据集之中,IDRN依旧能够保持极高的预测精度与稳定性,精度甚至略高于CFD,这表明IDRN与数据集具备极高的可行性与有效性.
IDRN与BPM、CFD对KP505的敞水性能预测值与其敞水试验值的对比如图13所示,IDRN预测KP505的KT与10KQ的相对误差分布如图14所示.
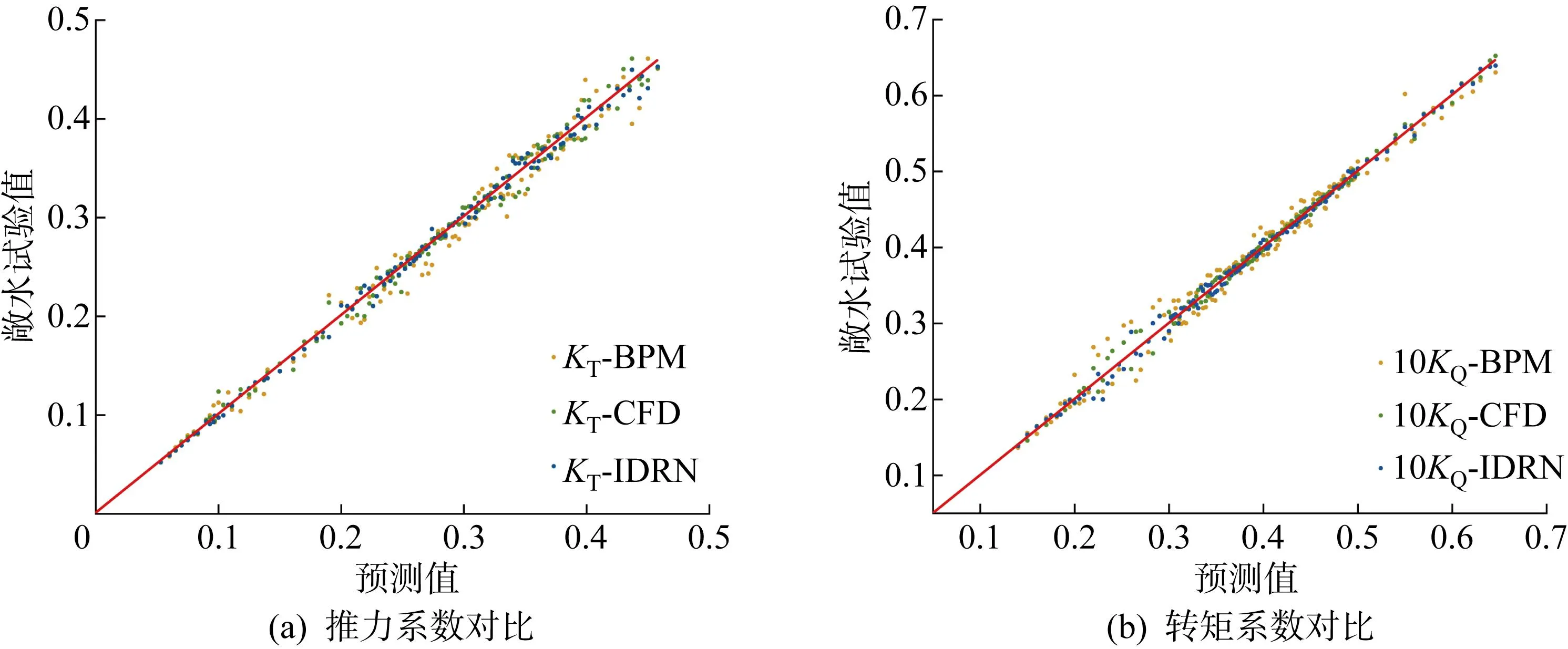
图13 IDRN、CFD法、BPM对KP505的预测值与其敞水试验值的对比Fig.13 Comparison of the predicted values of KP505 by IDRN, CFD, and BPM with the measured value of open water test
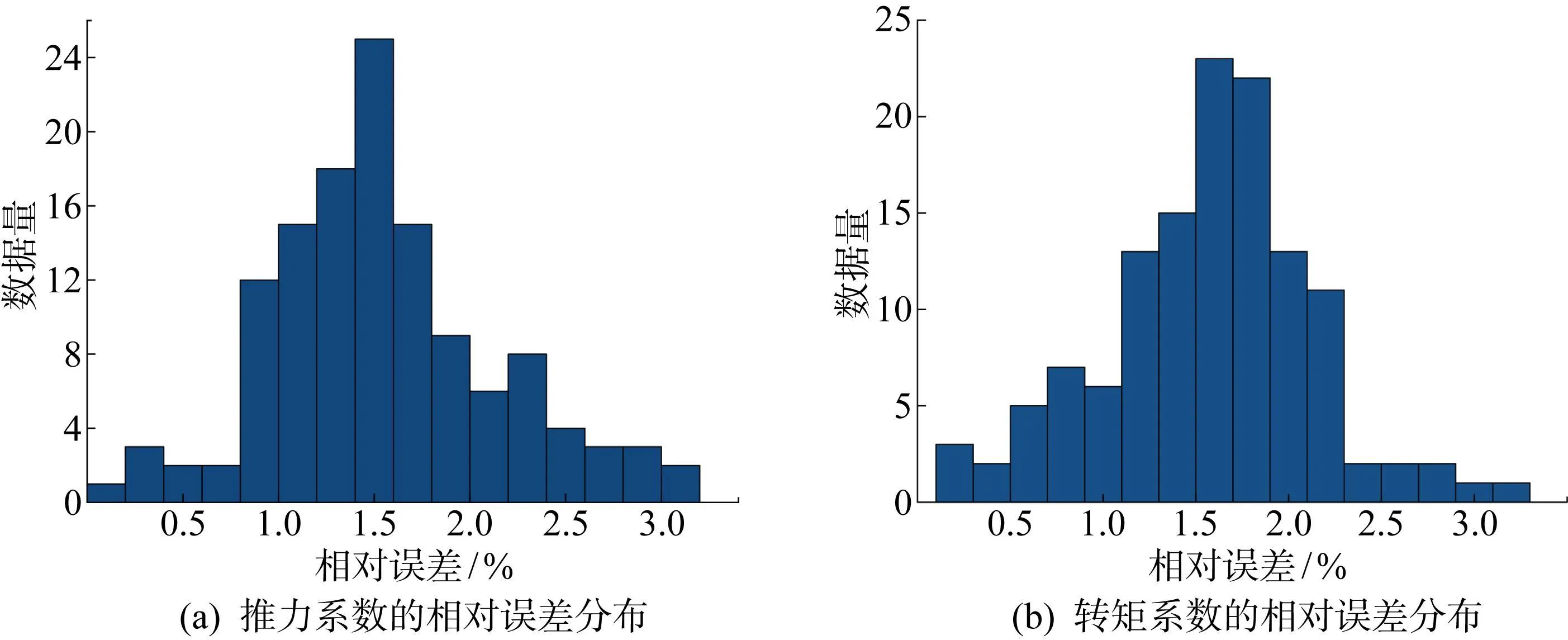
图14 IDRN对KP505的预测值的相对误差分布Fig.14 Distribution of relative error of the value predicted of KP505 by IDRN
KP505与数据集中所有螺旋桨均不属于同一系列桨,本实验旨在考察IDRN模型的稳定性与普适性.如图14所示,IDRN的预测值与敞水试验值的平均相对误差明显小于BPM,预测值的最大相对误差为3.12%,KT和10KQ的预测值中均仅有2个工况的相对误差超过3%,可见IDRN的精度与稳定性远好于BPM;CFD的预测值与敞水试验值吻合度较高,所有工况的相对误差均小于4%,在KT和10KQ的预测值中分别仅有2个和4个点相对误差超过3%,表现与IDRN相近.由图12可知,IDRN的相对误差主要集中在1%~2%的范围内,与预测B4-70敞水性能的实验相比,预测精度略有下降,但仍旧保持在与CFD基本持平的水平,预测稳定性依旧极佳,证明IDRN对预测不属于数据集中任何系列桨的某一螺旋桨依旧保有较高的精度,说明IDRN对桨叶几何参数与敞水性能间的映射关系的拟合度极高,表明IDRN模型具有极高的普适性与稳定性.
总的来说,CFD与IDRN的预测表现十分接近,但在以上的2个实验中,IDRN完成1个工况计算的平均用时仅为0.175 s,远小于CFD的计算周期,可以认为基本满足实时预报的需求.IDRN突破了传统CNN与BP神经网络在预测精度与预测范围的局限,使深度学习在螺旋桨设计阶段具备更高的工程意义.
3 结语
本文提出的IDRN,在残差连接结构的基础上与Inception结构相结合,大幅增加了网络的深度与宽度,使模型具备从多个不同尺度提取数据特征的能力,实现预测不同类型螺旋桨的敞水性能.
提出IBSAS算法,并开展优化性能研究,研究表明IBSAS算法比传统算法具备更好的优化性能,经其优化后的IDRN模型的收敛速度、精度、稳定性均大幅提高,过拟合问题也得以解决.
以KP505和B4-70桨为例,考察IDRN模型对数据集之外的螺旋桨的预测能力,验证其有效性与普适性.研究表明:模型预测值与实验值吻合度极高,偏差的分布十分集中,IDRN具备良好的预测稳定性,模型性能远高于BP神经网络模型,与CFD法几乎等同,在预测数据集内某系列桨性能时精度甚至略高于CFD法,对单工况预测的计算周期极短,可忽略不计.综上,基于本文方法建立的预测模型可以实现不同螺旋桨敞水性能的实时准确预报,提出的IBSAS算法在多参数模型的优化效率较传统算法有显著提高.
日后将加入与复杂工况相关的变量,让设计者们准确掌握螺旋桨复杂工况下的性能,便于进行优化设计.
