基于人因工程的船舶驾驶室人机界面布局优化设计

季煜恒, 李春通, 骆晓萌, 杨雪莲, 王德禹

(1. 上海交通大学 海洋工程国家重点实验室,上海 200240; 2. 上海交通大学 海洋装备研究院,上海 200240; 3. 中国船舶集团有限公司第十一研究所,上海 200032;4. 上海外高桥造船有限公司,上海 200137)

高性能人机界面具有标准化、易于使用和更高效的特征,可以使作业人员安全有效地完成监视和操作任务[1].较早开展人机界面研究的是1973年英国的一个研究机构,该机构开发了控制界面布局设计程序CAPABLE[2].1993年龙升照[3]系统地讨论了人-机-环境系统工程并应用于人机界面布局.进入21世纪后,各种人机界面研究蓬勃发展.在船海领域关于人机界面的研究以一维的布局优先序研究较多,如王帅旗[4]通过蚁群算法开展了工作站布局优化,人机设计与评价交互进行;马雨薇[5]考虑人体工程学因素,开发了舰桥导航设备的优化布局.陈登凯等[6]研究了包括显控装置在内的潜水器工作舱布局设计方法.最新的人机界面研究已步入智能化设计阶段:Hartman等[7]研究了智能轮椅上人机界面的交互与控制;Deng等[8-9]基于认知心理学理论,对钻机控制室的人机界面进行了优化设计,并进行了视觉美学相关研究;Lu等[10]基于多维感知研究了自动驾驶汽车的界面设计;Hao等[11]将机器视觉技术应用于人机界面的布局设计.新技术的诞生和日渐复杂化的工作流程都在推动船舶人机界面达到更高的性能水平.然而,目前国内关于船舶人机工效设计的规范与国外相比较为落后,舰船人-机-环系统工程缺乏完善的理论体系和模型化方法[12].因此,有必要开展人机界面布局优化研究,建立船舶驾驶室高性能人机界面设计方法.

目前关于人机界面布局问题的研究多数以提高界面空间、材料的利用率以及降低成本为核心,而鲜有在人机界面的布局设计中考虑人的身体特征、认知规律和心理特性等需求[13].另外,对人机界面的设计评估多以定性分析为主,或者以某单一因素为研究对象,缺乏系统的定量研究.因此,从人机工效的角度对驾驶室工作站人机界面的布局进行优化与评估具有非常重要的意义.本文在设计初期将人因工程学理论融入优化数学模型,使布局设计更加科学合理的同时,也能极大地提高优化设计的效率.

以船舶驾驶室工作站人机界面的布局优化设计为目标,以控制面板为研究对象,构建了人机界面二维布局优化模型,将人因工程学准则量化分析后与优化模型相结合,采用差分进化算法和粒子群算法进行优化迭代.对最终获取的优化布局方案进行虚拟仿真评价.本文提出的布局优化方法,适用于不同船型、操作方式、人体差异下各工作站面板的布局设计,可为提高船舶驾驶室工作站人机界面的布局设计效率、合理性、作业人员的工作效率和舒适度提供支撑.

1 人机界面布局优化的问题描述和数学建模

1.1 问题描述和相关假设

主要研究控制面板的布局优化问题.对于工作站面板的布局优化设计应当在驾驶室设计、工作站设计与布置、各显控装置设计已经完成并且合理合规的基础上进行.根据规范以及现有的工作站面板形式,假定工作站面板和待布局的装置为矩形结构,装置四边与面板四边平行,原点定义为作业人员位置,如图1所示.图中:O为面板原点;A、B为面板的长、宽;Ai、Bi为第i个装置的长、宽;xw、yw为第w个装置中心点的横、纵坐标;xiw为i和w间的横向间距,yij为i和j间的纵向间距;xvo为第v个装置与面板边界的横向距离,yvo为与面板边界的纵向距离.

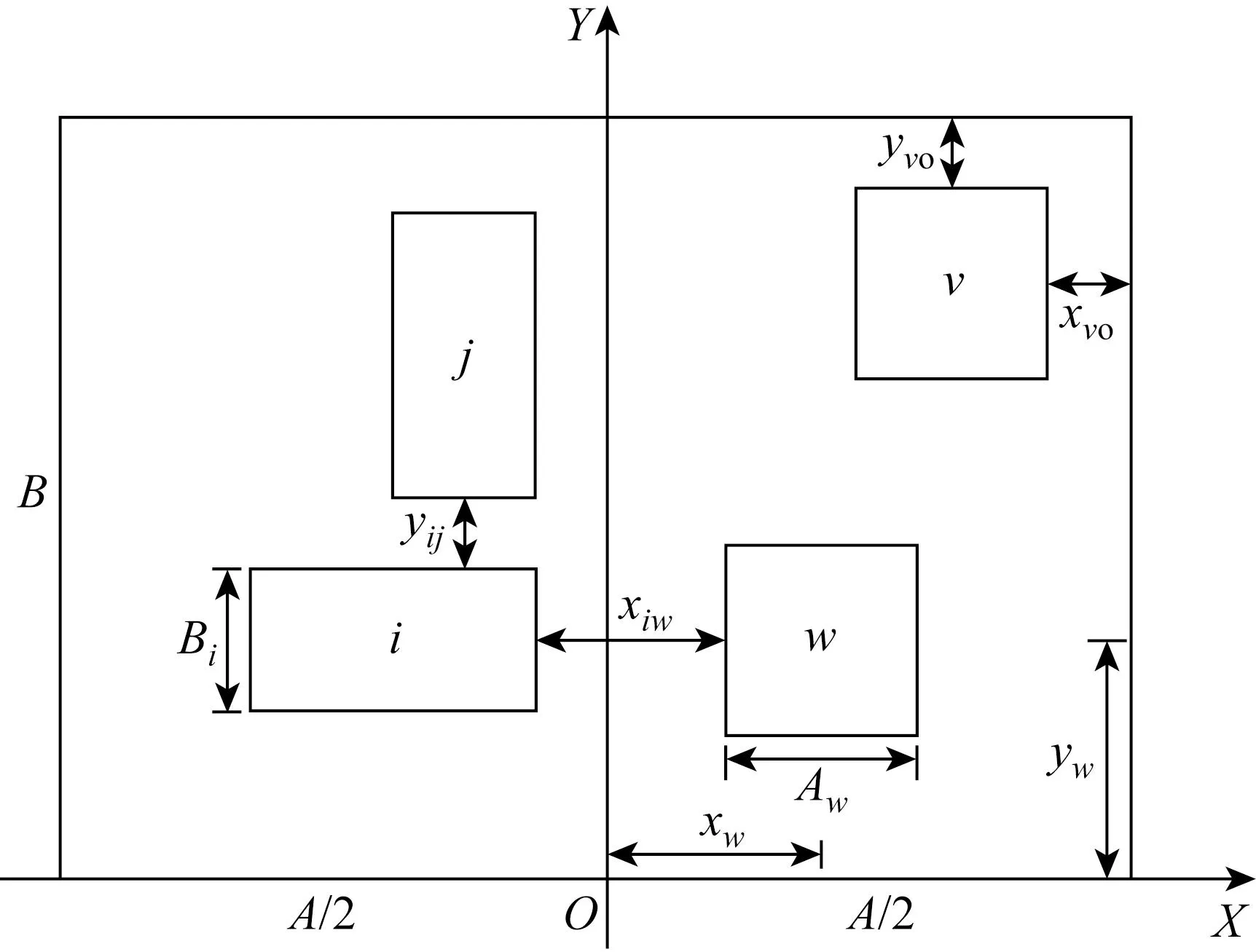
图1 面板和装置坐标图Fig.1 Coordinate diagram of panel and equipment

1.2 布局准则和人因工程学准则

结合国内外规范中的显控装置布局准则和人因工程学准则,船舶驾驶室工作站面板布局应当重点考虑以下原则.

(1) 功能分组原则.相同功能的元件应当进行集成化设计.

(2) 重要性原则.重要性高的装置应当布置在最优、最易观察或操作的位置.

(3) 使用频率原则.使用频率越高的装置应当布置在操作舒适度越高的位置.

(4) 顺序原则.在进行布局排列时,在各项任务中优先使用的装置应当靠左和靠上进行布置.

(5) 相关性原则.相关性越高的装置应当靠的更近.

(6) 空间相容原则.装置之间、装置与面板边界应当按照保留一定的间距.

1.3 布局优化数学模型

很多学者在车间、舱室等布局优化设计的数学模型建立方面已经进行了大量详细的研究[14-15].基于前文的问题描述和相关假设,本文在常规布局优化数学模型的基础上结合量化分析后的人因工程学准则建立船舶驾驶室人机界面的布局优化数学模型.以功能分组原则为设计前提,以重要性原则、使用频率原则、顺序原则和相关性原则作为子目标并构建目标函数,以空间相容原则为约束条件,进行数学建模.设计变量为每个装置的中心点在面板上的坐标(xi,yi).

1.3.1目标函数 分别建立重要性原则、使用频率原则、顺序原则和相关性原则4个子目标函数.定义待布局装置数量为n,船舶作业任务有k项.

(1) 重要性子目标函数:

(1)

式中:D(i)为第i个装置中心到最优操作点的距离,其中最优操作点位置人机交互虚拟仿真确定;Dm为面板上距离最优操作点的最大值;Pi为装置i的重要性权值.

Pi越大,表示装置i的重要性越高.应当由多位有经验的专家对不同装置的重要性进行协同打分,将各专家的评分取均值,作为各装置的重要性评分pi.分值为1～5分,分别表示绝对不重要、比较不重要、中等重要、比较重要和绝对重要.Pi的计算公式如下:

(2)

(2) 使用频率子目标函数:

(3)

式中:Ci为装置i所在面板区域的作业舒适度权值,通过人机交互虚拟仿真确定;Qi为装置i的使用频率权值.

IACS Rec.95[16]对不同工作站和不同任务下对各装置的使用情况进行了说明.Qi体现待布局装置的使用频率,Qi越大,装置i的使用次数越多.Qi通过统计对应工作站某航行任务内所负责的各作业任务的平均次数N,以及各作业任务中装置的使用次数uij进行确定,如uij=2代表装置i在任务j中被使用2次.Qi的计算公式如下:

(4)

(5)

(3) 使用顺序子目标函数:

(6)

式中:Si为装置i的顺序权值.

Si体现待布局装置的使用优先度,Si越小,装置i的使用优先度越高.Si通过统计各作业任务中装置的使用顺序来确定.Si的计算公式如下:

(7)

式中:si为装置i的顺序均值,

(8)

Mij为装置i在任务j中的使用顺序值之和.若装置i在任务j中被使用2次,且使用顺序为第2和第4个被使用,则Mij=6.

(4) 相关性子目标函数:

(9)

式中:dij为装置i和装置j的距离;dm为面板上两装置的最远距离;rij为装置ij间的相关性权值.

rij体现待布局装置间的相关度.rij=0,则装置i、j完全不相关;rij越大,装置i与装置j的联系就越大;rii=1.rij应由多位有经验的专家进行协同评估,将各专家的评估值取均值,作为各装置间的相关性权值.

(5) 子目标函数均已为无量纲函数,采用加权平均法将4个子目标函数合成为总目标函数:

f=ω1f1+ω2f2+ω3f3+ω4f4

(10)

式中:f为总目标函数值,体现布局方案的合理性;ω1为重要性子目标权值;ω2为使用频率子目标权值;ω3为使用顺序子目标权值;ω4为相关性子目标权值.子目标权值体现各子目标的重要度,可针对不同航行任务、工作站类型等具体需求按需设定,但应满足:

ω1+ω2+ω3+ω4=1

(11)

1.3.2约束条件 根据空间相容性原则构建约束条件如下.

(1) 边界约束.装置不应超出面板边界,并且应当与面板边界保持一定间距.

(2) 间距约束.装置不能发生重叠,且装置间应当保持一定间距.GB/T 14775—1993[17]中规定了控制装置的允许间隔距离和最佳间隔距离.

(12)

(13)

当式(12)或(13)满足条件时,装置i和j满足间距约束.

2 人机交互虚拟仿真和布局优化算法

工作站人机界面布局优化流程如图2所示,通过虚拟仿真确定人机界面的最优操作点位置和各区域的舒适度权值;采用差分进化算法获取粒子初始位置;通过粒子群算法进行优化迭代计算获得最优布局解;最后再通过虚拟仿真验证布局合理性.

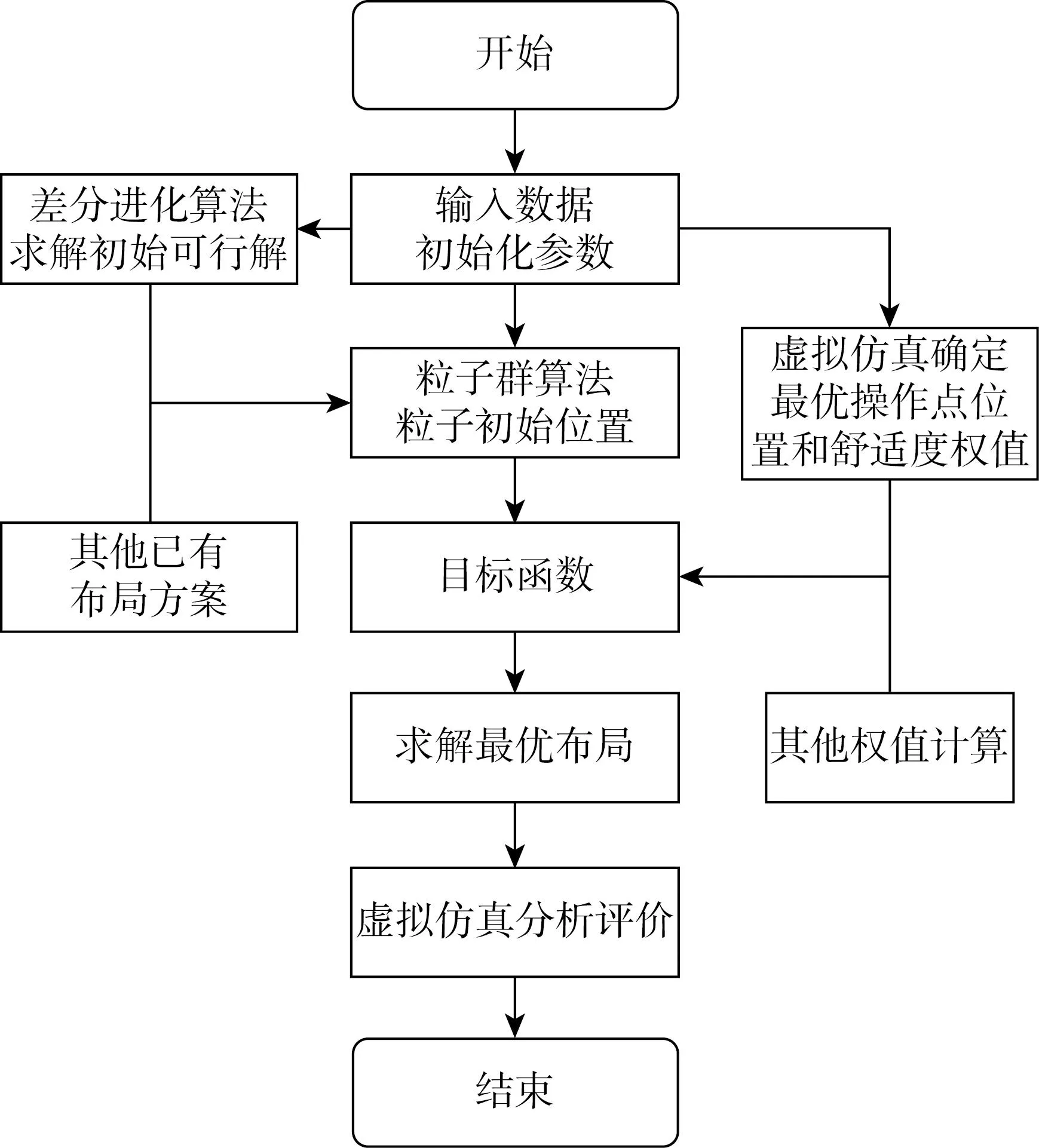
图2 布局优化流程图Fig.2 Flow chart of layout optimization

2.1 虚拟仿真

通过虚拟仿真来获取待布局工作站面板的最优操作点位置以及各区域舒适度权值,使用 Delmia 软件进行人因工程学虚拟仿真.

2.1.1建立人体和工作站虚拟模型 基于Human Builder模块建立不同百分位数的三维人体模型,并定义相应的操作姿态.将待优化的工作站面板模型(文件格式为.stl)导入仿真系统.

2.1.2快速上肢评估与面板各区域舒适度权值划分 快速上肢评估(Rapid Upper Limb Assessment,RULA)通过对人体姿势、用力情况、肌肉使用情况的研究来评估工作相关肌肉骨骼损伤的风险大小[18].采用RULA分析船舶驾驶室工作站作业人员的操作舒适度.RULA的评价结果为1～7分,并划分为4个级别,如表1所示.

表1 RULA评估分数Tab.1 Assessment score of RULA

当前各规范中对工作站面板的各区域舒适度与可达性仅有简单的描述和划分.为了对各区域舒适度进行量化分析,对待布局面板进行网格划分,并对人体手部触及各网格中心点时的姿势进行RULA分析.兼顾RULA评分精度和区域划分要求,采用长、宽为0.2 m左右的网格,网格对称分布,如图3所示.在Human Activity Analysis模块中获取作业人员在操作不同面板区域时各部位的RULA评分,将各部位的RULA评分相加,得到网格i的RULA总分Ri,定义ci为网格i的舒适评分,ci越高的区域,操作舒适度越高.将ci最大的网格的舒适度权值Ci定义为1,ci最小的网格的舒适度权值Ci定义为0,其他网格在[0, 1]间线性插值,可以得到面板各区域的舒适度权值Ci.ci的计算公式如下:

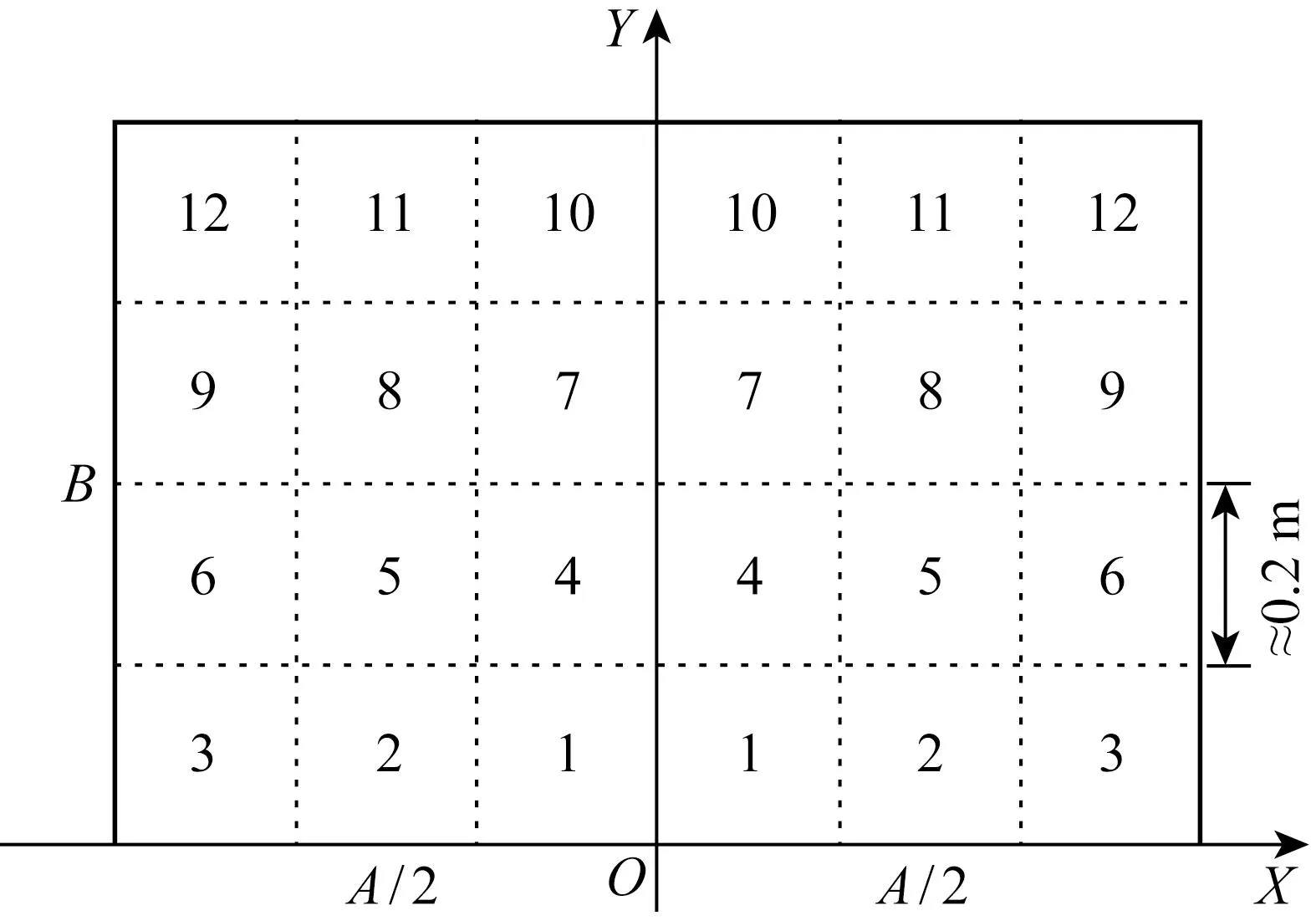
图3 面板网格划分与编号Fig.3 Meshing and numbering of panel

(14)

2.1.3姿态分析与最优操作点位置 MSC/Circ.982[19]中规定最重要的装置应当布置在最优、最易触及的位置,最优操作点位置的确定仍是一项难题.本文认为最优操作点为作业人员在最优作业姿态下,最易触及的工作站面板位置,该点也为整个面板操作舒适度最高的位置.为了准确获得该点位置,需要进行相比RULA分析参数更多、结果更精细的姿态分析.在Human Posture Analysis模块中对人体各部位设定角度界限与首选角度.为简化评估过程,对人体模型各部位首选角度按照3个等级进行划分,如表2所示.其中,可达域的上下边界为角度界限.接下来使用查找最优姿态功能,人体模型自动调整为最优姿态.可通过RULA分析验证当前姿态是否为舒适度最高姿态.再通过最少的调整使人体模型以更高的姿态评估分数接触到工作站面板,接触点为最优操作点.

表2 首选角度等级表Tab.2 Rating of preferred angles

2.1.4虚拟仿真分析评价 在完成优化求解得到优化布局结果后,对布局结果再次进行虚拟仿真,验证其可视性、可达性与舒适度,提出改进意见.

2.2 粒子群优化算法

粒子群优化算法通过粒子间共享信息,在个体历史最优和全局历史最优的共同作用下,向下一个方向寻优[20].粒子群算法参数少且寻优能力强,本文采用粒子群算法进行全局寻优.粒子群算法中基于式(12)和(13)以罚函数形式施加间距约束[21].在实际进行布局优化时,若待布局装置数量多且面板剩余空间小,采用常规的随机粒子初始位置难以获取满足间距约束的最优解.面对严格的间距约束,往往计算效率低下.因此,还需要获取大量满足间距约束的初始布局方案,作为粒子的初始位置.

2.3 差分进化算法求解初始位置

差分进化算法是一种基于群体智能理论的全局寻优算法,通过变异、交叉和选择操作来实现进化[22].采用常规的变异、交叉操作,选择操作为统计个体中满足间距约束的装置对数T,每当式(12)或(13)满足条件时,T增加1,选择T更大的个体作为下一代的初始种群.若T=n(n-1)/2,则所有装置保持一定间距,当前布局满足间距约束,结束运算,并输出满足空间相容性原则的解.通过差分进化算法可获得大量满足空间相容性约束的解,作为粒子群算法的粒子初始位置[23].

3 算例研究

3.1 参数确定与虚拟仿真

工作站和人机模型如图4所示.以国产化大型远洋客船H1508的导航与操纵工作站(型号:YA/865-SECT.E)的大面积控制面板作为算例进行布局优化设计,如图4(a)所示.首先确定工作站操作方式、尺寸、待布局装置数量、各装置尺寸、各项权值以及人体模型各部位首选角度.该控制面板长度A=1.416 m、宽度B=0.938 m.面板上各装置以按功能分组原则进行分组,分组与命名参考规范IACS Rec.95[16]和MSC/Circ.982[19],分组后待布局装置的编号、尺寸和初始坐标如表3所示,各装置的重要性权值、使用频率权值、顺序权值和相关性权值采用1.3.1节中的方法进行计算,其中涉及主观评价的数据参考文献[4].

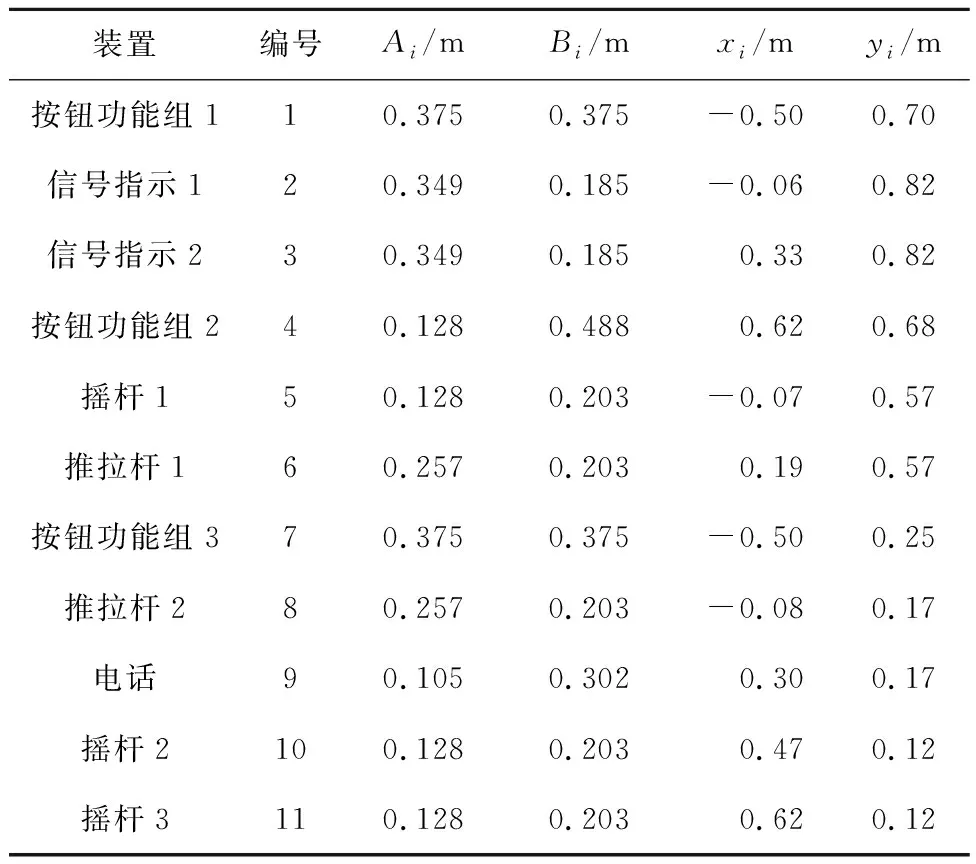
表3 装置编号、尺寸和初始坐标Tab.3 Number, size, and initial coordinates of equipment

图4 工作站和人机模型Fig.4 Workstation and human-machine model

该控制面板由作业人员站立操控,本文使用的人体模型数据来源于GJB/Z 131—2002[24]中舰艇人员的人体测量数据.案例中的工作站面板面积较大,构建第95百分位的人体模型,导入工作站模型,建立人机交互模型,如图4(b)所示.对虚拟人体模型在1～12号网格区域的作业姿态进行RULA分析,获取手腕、前臂、上臂、躯干的RULA评分,求得各网格的舒适评分ci和面板各区域的作业舒适度权值Ci如表4所示.

表4 第95百分位舒适度权值Tab.4 Comfort weight of 95th percentile

人体模型各部位首选角度设定参考文献[25].所得最优姿态如图5所示, 最优姿态与标准站立姿态相比上臂略微外展,前臂微屈.对当前所得最优姿态进行RULA分析,各部位以及综合RULA评分均为1,首选角度设置合理.由最优姿态获取最优操作点坐标为(±0.3 m, 0.17 m).

图5 最优姿态Fig.5 Optimal posture

3.2 差分进化算法求解初始解

综合考虑计算效率和需要的初始可行解数量,设置种群个数为250,空间维数为22,最大迭代次数为500.采用线性递增的缩放因子和交叉概率,避免个体过早趋同,经过多次计算验证,设置最小缩放因子为0.1,最大缩放因子为0.9,最小交叉概率为0.1,最大交叉概率为0.6时,可高效获得初始可行解.允许最小间距均为0.03 m.计算出 1 999 组初始可行解,其中一组初始可行解如表5所示,加入表3中的初始设计方案,得到 2 000 组初始可行解.

表5 初始可行解Tab.5 Initial feasible solution

3.3 粒子群算法求解最优布局

读取初始可行解,合理设置种群个数、空间维数和最大迭代次数使得算法能够快速收敛.设置粒子个数为 2 000,空间维数为22,最大迭代次数为500.采用目前较为常用的线性递减惯性权重,设置最小惯性权重为0.6,最大惯性权重为1.经过多次计算验证,速度下界为-0.5,速度上界为0.5,自我学习因子为0.4,群体学习因子为0.6时,可高效获得最优布局解.文献[4]中在认为子目标同等重要时, 设置相同的子目标权值.本算例中认为4个子目标同等重要,考虑到式(11),因此4个子目标权值都取为0.25.粒子群算法迭代过程如图6所示.多次求解得最优布局方案如图7所示,各装置编号与图4(a)相同.对应的最优布局解坐标如表6所示.

表6 最优布局解Tab.6 Optimal layout solution

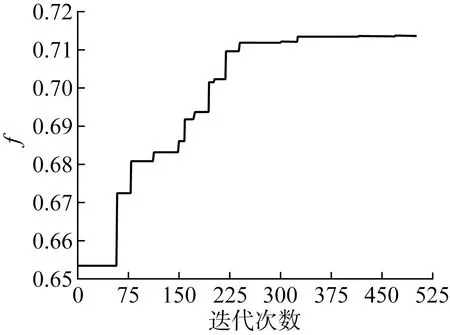
图6 粒子群算法迭代曲线Fig.6 Curve of PSO iteration

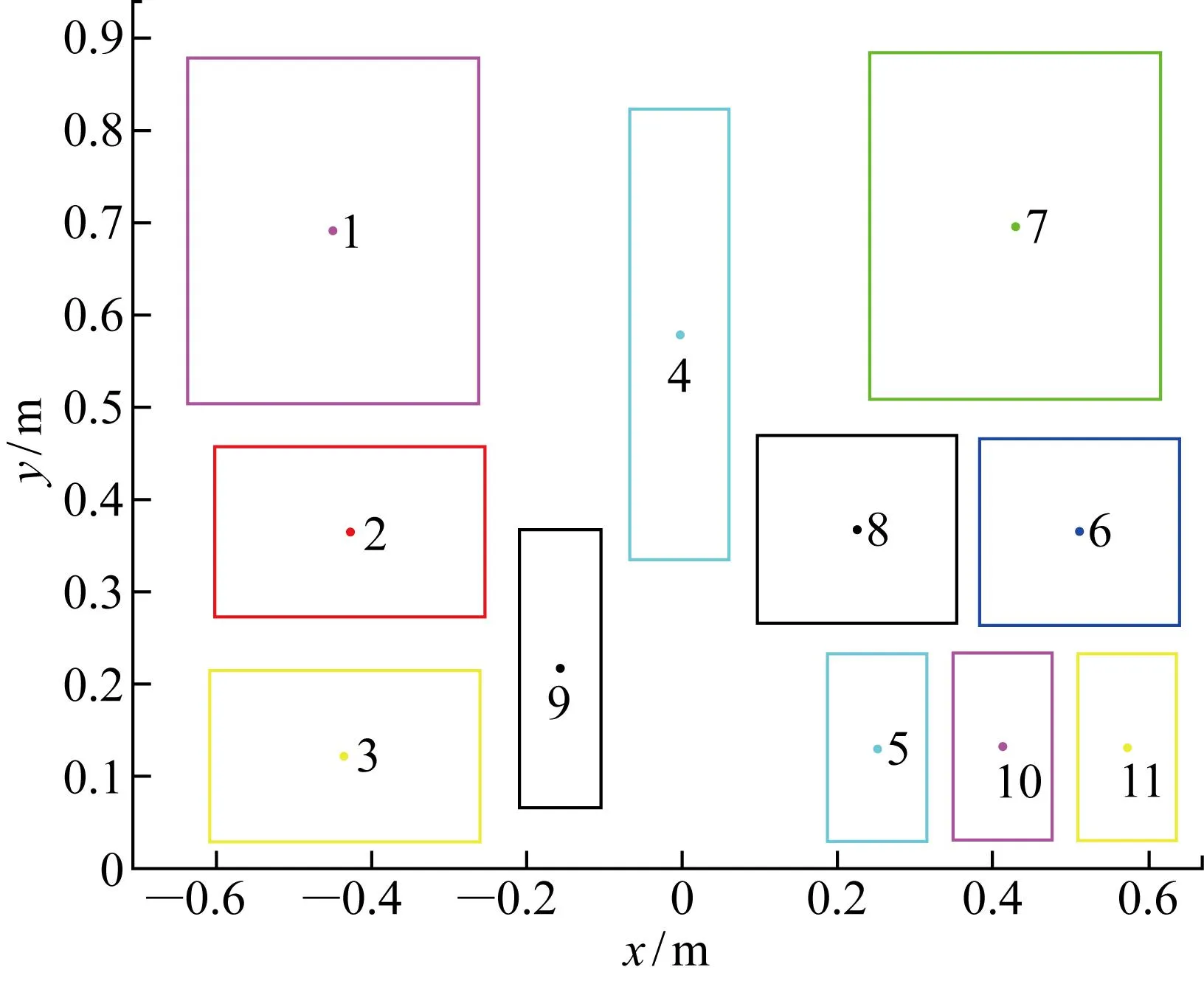
图7 第95百分位最优布局图Fig.7 Optimal layout of 95th percentile

3.4 人体模型参数差异对比

对于人机界面的优化设计,人体尺寸数据是人因分析的重要输入,影响不可忽略[26].选取与第95百分位差异较大的第5百分位人体数据进行对比试验,探讨人体参数变化对人机界面布局优化设计的影响.构建第5百分位的人体模型,与人体参数无关的其他参数与前文第95百分位的人体模型算例保持一致.

通过RULA分析,得到面板网格1～12的Ci分别为1.00,1.00,0.79,0.69,0.39,0.29,0.29,0.29,0.19,0.09,0.09,0.00.人体模型各部位首选角度不变,进一步通过姿态分析确定此时的最优操作点坐标为(±0.3 m, 0.155 m).对比表4和表7可知,相比第95百分位,第5百分位下原本舒适度较高的区域舒适度进一步提高,而原本舒适度较低的区域舒适度进一步降低.但面板各区域的相对舒适度关系没有变化,且最优操作点位置也仅略有改变.进一步求解得第5百分位最优布局方案如图8所示.对比图7和图8,仅各装置略有小幅度位移,而相对位置关系没有变化.因此,在本算例中,人体参数在合理范围内的改变对布局设计的结果影响很小.

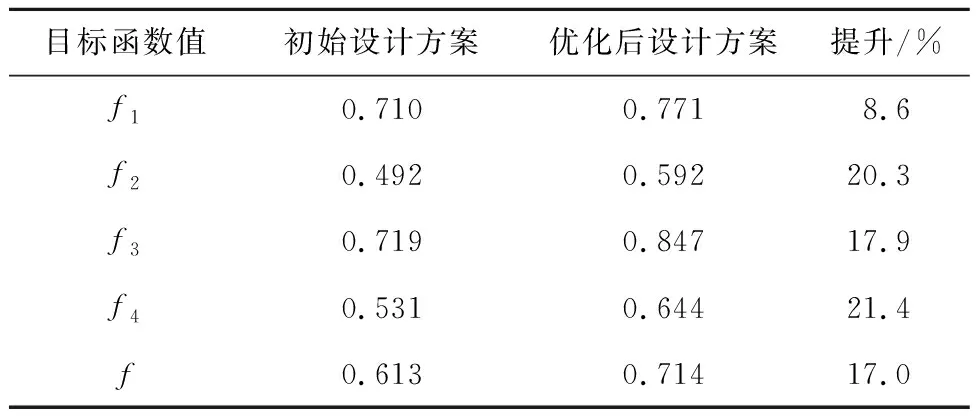
表7 目标函数对比Tab.7 Comparison of objective function

图8 第5百分位最优布局图Fig.8 Optimal layout of 5th percentile

3.5 虚拟仿真评价

考虑到本算例中,人体参数的改变对布局优化结果影响较小,因此使用Delmia软件对第95百分位人体参数下的最优布局方案开展人机交互虚拟仿真与评价.

3.5.1可视性分析 GJB 2873—1997[27]规定,头部自然向上、向下、向左、向右转动15°范围内为最佳视角区域.捕捉站立姿态(视线水平向前)及低头15°(垂直视角内视线向下15°)时的视野如图9所示.站立姿态平视前方时,工作站面板遮挡有限,正前方仍有良好视野.人体模型低头15° 时,控制面板均在可视域内,相关控制装置清晰可见.所有装置都在最佳视角区域内,当前工作站布局满足可视性要求.

图9 视野分析Fig.9 Vision analysis

3.5.2可达性分析 由GB/T 14779—1993[28]可知,在坐姿的情况下,身体前倾的舒适角度应小于25°.对于站姿情况,仅改变身体前倾角度,可测得躯干的RULA评分.前倾0°～20° 时,躯干的RULA得分小于2;21°～56° 时,躯干的RULA得分小于4.因此,认为在站姿的情况下,身体前倾的舒适角度应小于20°,作业角度应小于56°.显示人体模型在身体前倾20° 时的上肢伸展域作为舒适可达域,56° 时的上肢伸展域作为作业可达域,如图10所示.

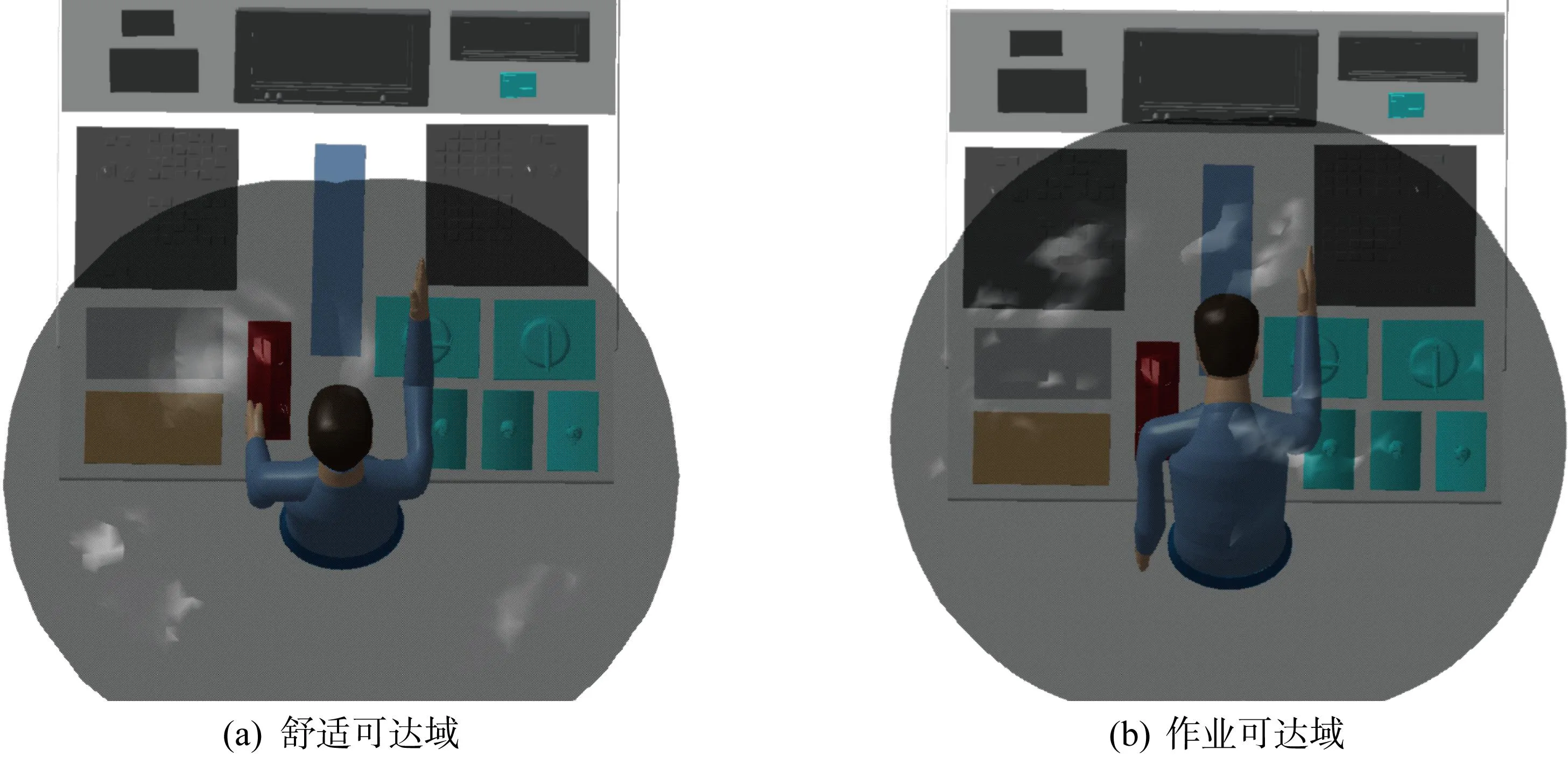
图10 上肢伸展域Fig.10 Upper body extension

当前布局下,63.6%的装置在舒适可达域内,重要性和使用频率较高的装置也都在舒适可达域内,且所有装置都在作业可达域内.采用孙守迁等[29]提出的可达性评价方法:

(15)

式中:E为可达性评分;Z为最远可达距离.

评价结果E在[0,1]间,当E<0.5时,认为系统可达性可行.对于当前布局,在站姿操作下Z为0.8 m,E=0.35.若限制到舒适可达域,Z取0.6 m时,E=0.47,可认为当前布局满足可达性要求.若该控制面板采用坐姿操作,则Z=0.4 m,E=0.70,可达性较差.若控制面板宽度较大,则不适合采用坐姿操作.

3.5.3舒适度分析 初始设计方案和优化后设计方案的4个子目标函数值如表7所示.相比初始方案,优化后的布局方案更好地满足了所有子目标原则.其中,使用顺序原则和相关性原则子目标函数的提升,表明优化后的布局方案提升了工作效率,降低了操作失误率.而使用频率原则子目标函数最能体现布局方案的舒适度,优化后的布局方案舒适度提升显著.总目标函数体现布局方案的合理性,依据式(10),在各子目标权重相同时,布局合理性提升了17.0%.

4 结论

(1) 以船舶驾驶室工作站的人机界面为研究对象,通过虚拟仿真将人的身体特征、认知规律和姿态舒适度量化并融入目标函数,建立了对重要性、使用频率、使用顺序与相关性这4个指标的布局优化数学模型.借助差分进化算法丰富了初始种群多样性,并采用粒子群优化算法高效地获得了最优布局方案,布局合理性提升了17.0%.

(2) 通过Delmia虚拟仿真模拟作业人员的实际操作姿态,验证了现有控制面板能够满足可视性和可达性两个基本需求,且优化后的布局方案提升了作业人员的操作舒适度和工作效率.通过虚拟仿真可以对作业人员姿态进行定性校核和定量评价,为人机界面的人机性能研究提供理论依据.

(3) 本文提出的布局优化方法可移植性强,通过建立不同场景下的各项权值、操作舒适度、最优操作点位置等数据库,结合适度的人工输入以满足实际场景需求,本研究可以为实现智能化人机界面的高效自动布局提供支撑.