波浪中的螺旋桨水动力性能数值分析
2024-03-04姚建喜
张 耕, 姚建喜,b
(武汉理工大学 a. 高性能舰船技术教育部重点实验室; b. 船海与能源动力工程学院, 武汉 430063)
螺旋桨是目前最常用的船舶推进器,其水动力性能与船舶的快速性和经济性密切相关,对螺旋桨水动力性能进行预报分析是螺旋桨设计工作的重要内容之一[1].蔡荣泉等[2]采用雷诺平均NS(RANS)方法研究螺旋桨的敞水性能,发现在桨叶的叶背表面,最大负压区域集中在内部的弯凸部位,叶梢轮廓两侧叶面与叶背间的压力连续变化.刘志华等[3]采用RANS方法对不同叶数、不同侧斜度和不同剖面形式的螺旋桨的敞水性能进行了数值预报,计算结果与试验数据吻合较好.Yao[4]采用RANS方法对斜流中螺旋桨的水动力性能进行了数值预报,在多种进速系数和攻角组合的情况下,得到了螺旋桨的推力及转矩,以及螺旋桨盘面在旋转一周过程中的平均推力分布.王超等[5]采用RANS方法,对敞水中螺旋桨的桨叶表面压力分布进行了考察与分析,发现桨叶压力面上的压力由叶根至叶梢先增大后减小.
以上研究仅考虑螺旋桨在无限水深条件下的水动力性能,而不考虑自由面、波浪等的影响.实际上,这些因素在一定条件下,对船后工作螺旋桨的性能有很大影响.近年来,国内外学者基于水池试验结果并结合理论分析,针对存在自由面且无波浪条件下的螺旋桨水动力性能进行了研究.例如,Califano等[6]采用RANS方法研究螺旋桨在自由面附近的水动力性能,发现在螺旋桨旋转过程中,与静水中不存在自由面的情况相比,推力及转矩出现周期性振荡,且单片桨叶的振荡幅度更大.Kozlowska等[7]研究了浸深对螺旋桨水动力性能的影响,发现当进速系数较大时,螺旋桨推力的数值计算结果与试验数据较为吻合,而当进速系数较小时,数值计算结果与试验数据相差较大.张磊等[8]采用RANS方法计算分析了浸深与进速系数对螺旋桨水动力性能的影响,发现当浸深与进速系数较小时,螺旋桨的推力及转矩易发生突变,且桨叶受力脉动更加剧烈.
此外,船舶在海上航行时,不可避免地会受到波浪的作用,船体会产生摇荡运动,此时船后工作的螺旋桨可能会刺穿水面,与空气发生接触,产生吸气、飞车等现象,导致螺旋桨的推力及转矩减小、效率下降.不仅如此,螺旋桨周期性出入水面,会导致桨叶产生负荷脉动变化,进而引起发动机转速及功率的巨大变化,影响螺旋桨和船舶动力系统轴系的强度.在较大的波浪作用下,螺旋桨性能的恶化还可能导致船体失去控制,威胁船舶航行安全.曹梅亮[9]开展了波浪中不同浸深条件下的螺旋桨水动力性能试验,发现随着浸深减小,螺旋桨推力及转矩的平均值也随之减小,效率亦会下降,而当浸深较大时,螺旋桨在波浪中的推力及转矩曲线与无波浪时相同浸深下的曲线很接近.董国祥等[10]开展了一系列波浪中的螺旋桨水动力性能试验,研究了在浸深相同的条件下,波长对螺旋桨推力、转矩和效率的影响,发现波浪中螺旋桨的推力增量、转矩增量在短波段的变化比长波段大,且在波浪中选取不同的进速系数时,推力增量、转矩增量的变化规律一致.Tokgoz等[11]采用RANS方法,对不同浸深与进速系数条件下波浪中螺旋桨的推力波动现象进行了研究,发现当浸深较大时,数值计算结果与试验数据吻合良好,而当浸深较小时,误差较大.尽管如此,与存在自由面且无波浪的静水条件相比,目前针对波浪中螺旋桨水动力性能的研究还相对较少.
本文采用RANS方法,数值预报存在自由面且无波浪的静水条件下和波浪中螺旋桨的水动力性能,分析浸深与进速系数对螺旋桨推力、转矩、桨叶表面压力分布和水面扰动变形的影响,在现有其他学者的研究基础上,进一步分析波浪中螺旋桨水动力性能的特点.
1 螺旋桨几何模型及计算工况
采用基于OpenFOAM的RANS求解器,数值预报螺旋桨在波浪中的水动力性能.研究对象为国际研究标准船模KVLCC2(The Second KRISO Very Large Crude Carrier)使用的螺旋桨,编号为KP458.数值计算时,螺旋桨的缩尺比取100,对应的KVLCC2垂线间长Lpp为3.2 m.螺旋桨的几何模型如图1所示.螺旋桨模型的主要参数为:直径 0.098 6 m;螺距比 0.721 2;盘面比0.431;毂径比0.155;桨叶数4.

图1 螺旋桨几何模型Fig.1 Geometry of propeller
为了将计算结果与文献[11]中的试验数据进行比较,验证计算精度,计算考虑的波浪参数与该文献中的参数一致,即规则波的波长取1倍船长(3.2 m),波幅取0.019 m,波陡为 0.011 9.计算时,螺旋桨转速n取30 r/s,但考虑了不同的浸深比与进速系数,具体工况为:J=0.20,0.35,0.50;I/R=1.20,1.60,2.00,3.39,4.00.螺旋桨浸深比(I/R)定义为螺旋桨旋转中心至无扰动水面的距离I与螺旋桨半径R之比,如图2所示.进速系数定义为
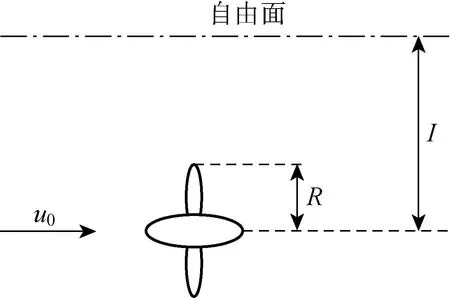
图2 浸深比的定义Fig.2 Definition of immersion depth ratio
(1)
式中:u0为来流速度;D为螺旋桨直径.
此外,为了对比分析波浪对螺旋桨水动力性能的影响,本文还计算了不考虑波浪的静水工况,但考虑了自由面的影响,具体工况为:J=0.15,0.20,0.25,0.30,0.35,0.40,0.50,0.60;I/R=1.20,1.60,2.00,4.00.
2 数值方法
2.1 流动控制方程
在空间直角坐标系O-xyz下,描述螺旋桨周围流体的流动,坐标原点O位于螺旋桨旋转中心,x轴指向来流方向,z轴垂直向下,如图3所示.
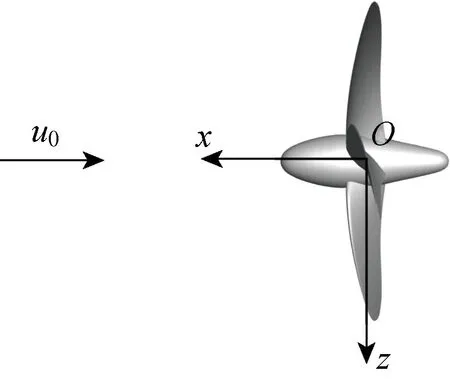
图3 坐标系示意图Fig.3 Definition of coordinate system
基于不可压缩的牛顿流体假设,螺旋桨周围的流体流动满足质量守恒方程(连续性方程)和动量守恒方程(RANS方程),其张量形式如下:
(2)

根据Bousinesq假设,雷诺应力可表示为
(3)
式中:νt为涡黏系数;k为湍流动能;δij为Kronecker系数.
采用SSTk-ω湍流模型[12]近似式(3)中的涡黏系数νt.
采用流体体积分数法(Volume of Fluid, VOF)捕捉自由面,流体体积分数F满足以下传输方程:
(4)
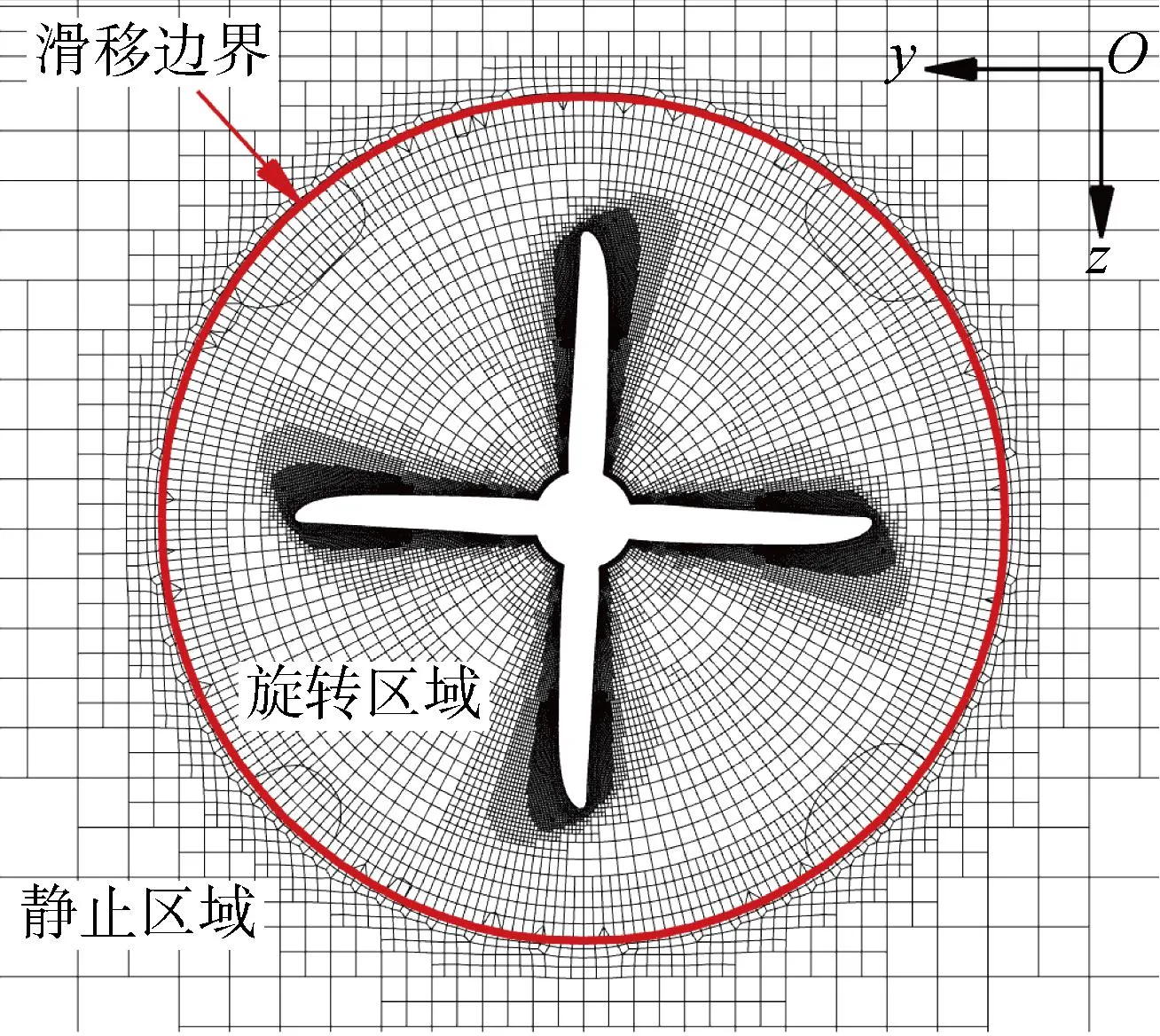
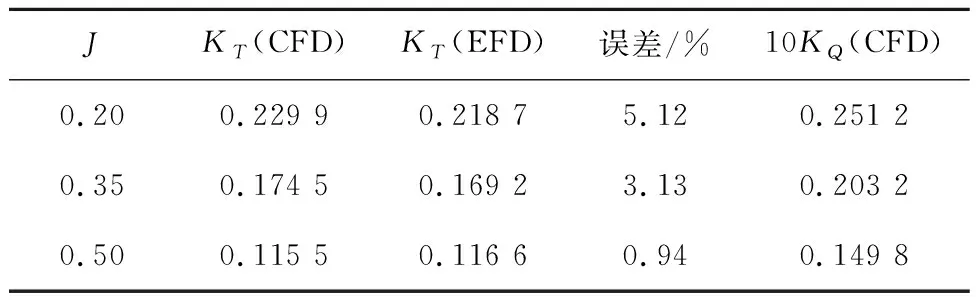
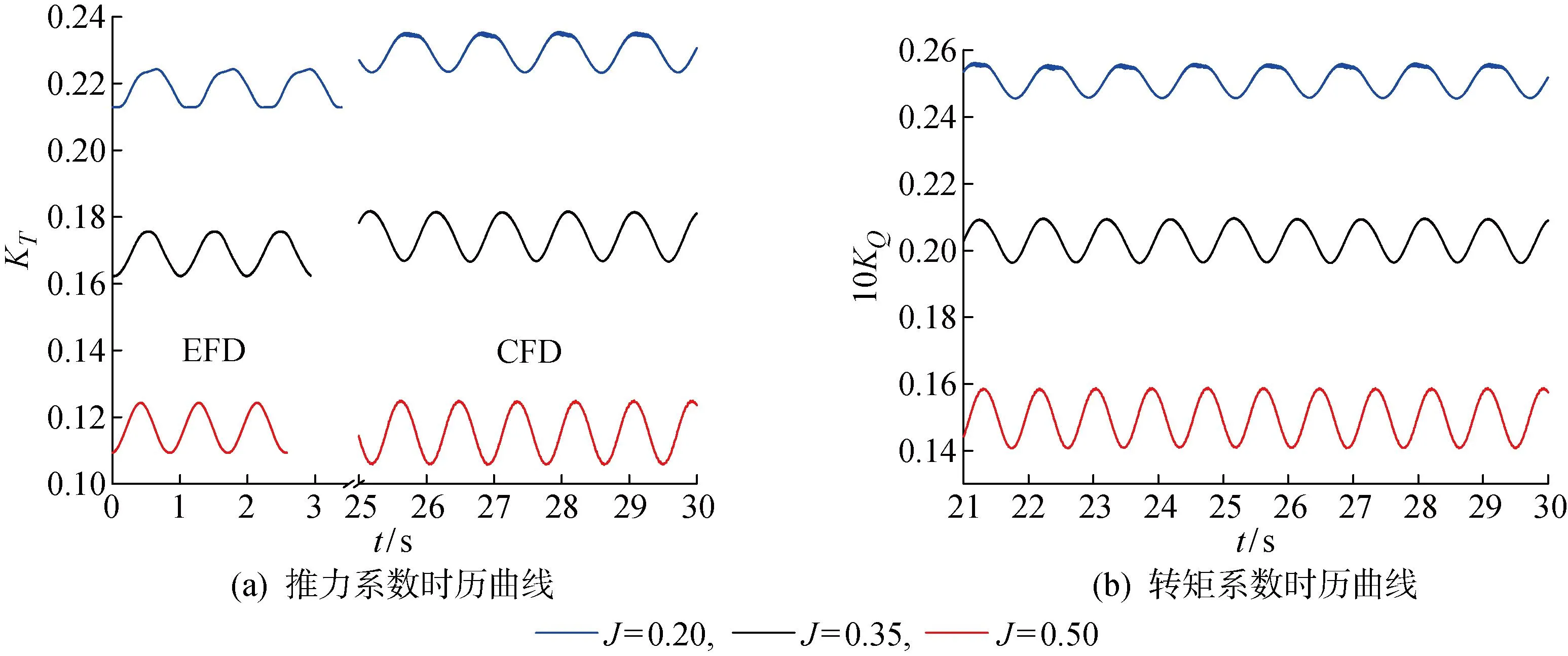
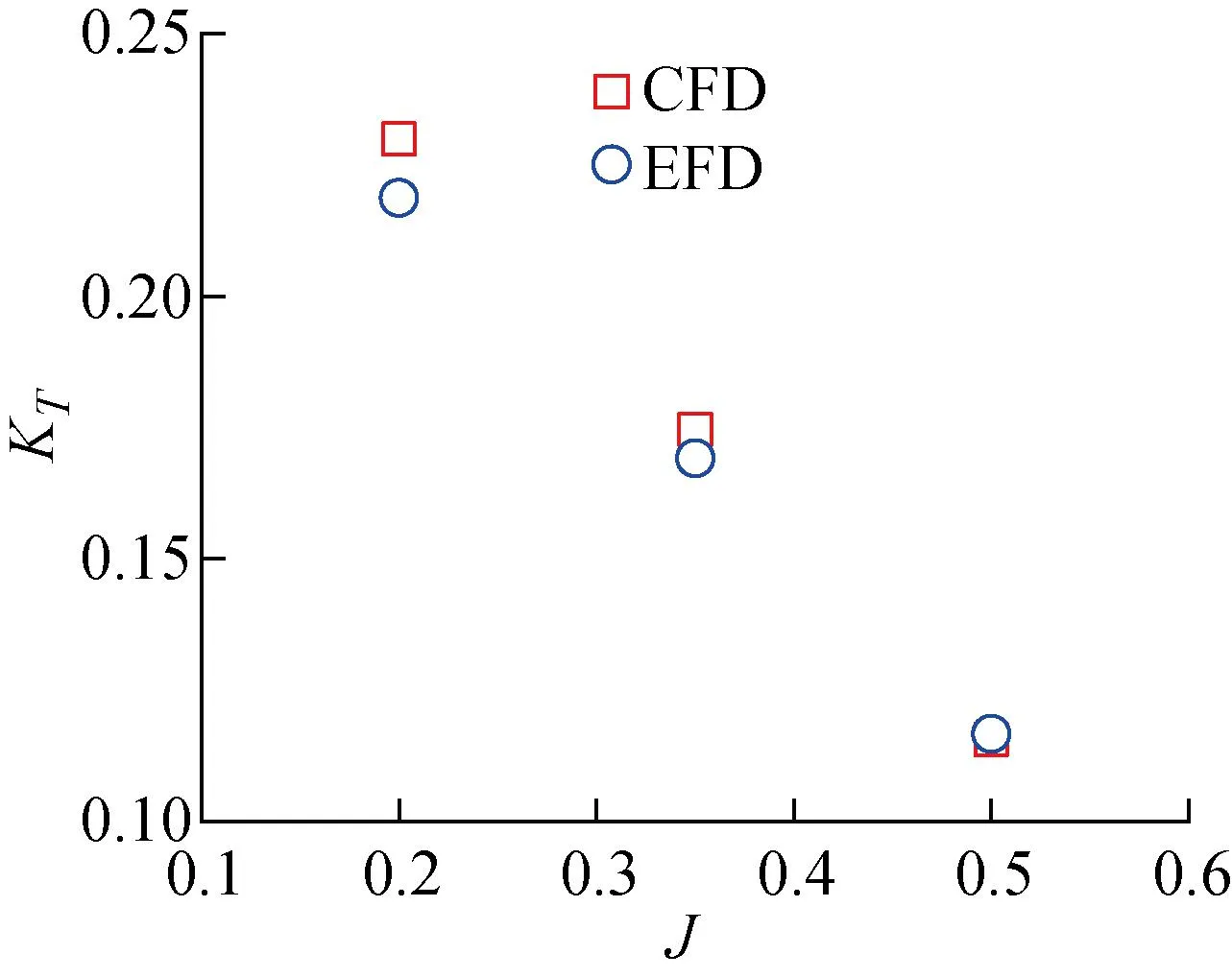
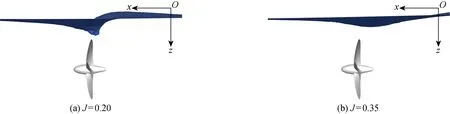
对于单个网格单元,若F=0,则该网格单元充满空气;若F=1,则该网格单元充满水;若0 (5) 式中:下标w和a分别表示水和空气. 数值计算的计算域取一长方体,其具体范围为-2.5Lpp≤x≤0.5Lpp,-10.14D≤y≤10.14D,-Lpp≤z≤Lpp,如图4所示. 图4 计算域示意图Fig.4 Computational domain 采用在远场边界上给定无扰动流场和波面的方法在计算域内数值造波,基于线性波浪理论,入口边界处(即x=0.5Lpp处的边界,见图4)的流速为来流速度与造波流速的线性叠加[14],即 (6) 对应的波面表达式为 ζ=-Asin(ωet+kwx) (7) 式中:ζ为波面升高. 为了保证计算精度,需要消除下游边界(即x=-2.5Lpp处的边界,见图4)反射波的影响.本文采用阻尼消波法在下游区域消波,在消波区域内RANS方程中的fi≠0,其表达式为 fi=(0,0,d(x)w) (8) (9) 式中:w为Ui的第3个分量,即Ui=(u,v,w);α为消波系数;xs为消波区域的起始位置. 在计算域的4个侧边界上,即y=±10.14D、z=±Lpp处,设置滑移边界条件;而在螺旋桨(桨叶、桨毂)表面上,设置壁面边界条件.具体边界条件如表1所示.表中:ω为比耗散率;β1=0.075,为湍流模型系数;yw为到壁面距离;kin和ωin由下式估算: 表1 边界条件Tab.1 Boundary conditions (10) 式中:It≈0.05,为湍流度;Cμ=0.09,为湍流模型系数;ls为湍流长度尺度,与网格尺度接近;uin为入流流速. 采用有限体积法(Finite Volume Method, FVM)求解流体动力控制方程,其中RANS方程中的扩散项和对流项分别采用中心差分格式和二阶迎风格式进行离散处理,时间项采用一阶隐式欧拉格式进行离散处理,湍流方程采用二阶迎风格式进行离散处理.压力速度耦合算法采用PIMPLE算法,即将SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)算法和PISO(Pressure Implicit with Splitting of Operators)算法相结合,利用“预报-校正”的策略,通过迭代的方式将速度场和压力场的耦合方程组解耦.对于由离散方程得到的线性方程组,采用高斯-赛德尔迭代法迭代求解流速、湍流动能和比耗散率,采用GAMG(Generalized Geometric Multi-Grid)法迭代求解压力[15]. 采用OpenFOAM中的滑移网格方法模拟螺旋桨的旋转运动.运用该方法时,计算区域被划分为包含螺旋桨几何形状的旋转区域和剩余的静止区域.在计算过程中,随着时间的步进,旋转区域围绕桨轴旋转,静止区域和旋转区域之间存在一对几何尺寸相同的滑移交界面(见图5),两个滑移交界面之间的流动信息(流速、压力等)采用面积分数法进行插值交换. 图5 滑移网格(x=0 m)Fig.5 Sliding grid (x=0 m) 本文使用商业软件Hexpress生成计算网格.圆柱体旋转域的直径为1.3D,高为0.7D;静止区域为长方体,范围如前所述:-2.5Lpp≤x≤0.5Lpp、-10.14D≤y≤10.14D、-Lpp≤z≤Lpp,其中Lpp=3.2 m.旋转域的中心位于静止区域内部x=0 m、y=0 m、z=0 m的位置,两者之间存在一对几何尺寸相同的滑移交界面.本文不采用壁面函数近似边界层内的流动,因此在生成网格时,将靠近壁面第1层网格与壁面间的无量纲垂直距离,即y+,控制在y+<1. 为了确保计算精度并尽量减少计算时间,首先开展了网格依赖性分析,计算工况为J=0.20、I/R=2.00.使用商业软件Hexpress生成了3套疏密程度不一的多面体非结构化网格,分别记为coarse、medium和fine.网格生成过程中,在x、y、z方向上使网格单元数量等比例增加.为了保证网格质量,在叶尖及叶边处,进行了加密处理.3套网格的网格单元总数分别为 357 494、692 314 和 1 350 755,其中旋转域的网格单元数分别为 269 196、491 250 和 932 883;静止域的网格单元数分别为 88 298、201 064 和 417 872.图6为fine网格的旋转域网格和静止域网格. 图6 Fine网格Fig.6 Fine grid 网格依赖性分析时,定义螺旋桨旋转一周的时间步数量为Ns.为了节省计算资源,在计算域内开始造波时,计算时间步长取0.005 s,直至流场稳定后再减小时间步长,取Ns=200.使用3套网格计算得到的螺旋桨推力系数(KT)及转矩系数(10KQ)时历曲线,如图7所示.可以看出,随着网格加密,时历曲线变得接近,其中采用medium网格和fine网格得到的计算结果已经十分接近. 注意到,图7中给出的是无因次推力及转矩时历曲线,其表达形式如下: (11) 式中:T为推力;Q为转矩. 采用3套网格计算得到推力系数KT的平均值分别为0.224 7、0.228 6 和 0.229 9,转矩系数10KQ的平均值分别为 0.249 5、0.251 3 和 0.251 2.由此可见,采用medium网格和fine网格的计算结果已经十分接近,继续加密网格,计算结果已不会出现显著的变化.但是,本文为获得更为细致的流场信息,仍采用fine网格对后续算例进行计算. 采用上述fine网格,对时间步长依赖性进行分析,Ns取100、200和400,对应的时间步长分别为 0.000 333 s、0.000 167 s和0.000 083 s.计算得到的时历曲线如图8所示.可以看到,随着时间步长减小,螺旋桨推力系数及转矩系数的时历曲线逐渐接近.采用3个时间步长得到的推力系数计算平均值分别为0.224 5、0.229 9 和 0.231 0,转矩系数计算平均值分别为 0.247 9、0.251 2 和 0.252 9,Ns取200和400得到的平均推力系数和转矩系数已经十分接近.若进一步减小时间步长,计算得到的推力系数与转矩系数的峰值估计会更加接近. 图8 时间步长依赖性分析Fig.8 Time-step dependency study 通过以上分析,可以看出,对后续工况的计算,采用fine网格且Ns取200,能够保证足够的计算精度. 此外,对数值造波、消波的效果进行了考察.图9给出了工况J=0.20、I/R=2.00在纵剖面y=0.99 m处的理论波形与数值波形.可以看出,在-0.5 m≤x≤1.6 m范围内(螺旋桨旋转中心位于x=0 m),计算波形与理论波形符合较好,波幅没有出现明显衰减.从x=-0.5 m起(消波起始位置xs=-0.5 m),波幅迅速衰减,在下游靠近出口边界处,波幅几乎衰减至0. 图9 造波消波验证Fig.9 Verification of wave-making and wave-elimination 首先对存在自由面且无波浪的静水条件下螺旋桨的水动力性能进行预报分析.为了验证计算精度,将推力系数及转矩系数的计算平均值与 SIMMAN 会议公开的KP458螺旋桨敞水试验数据进行比较,如表2、表3和图10所示.可以观察到:当I/R>1.60时,螺旋桨推力系数及转矩系数的计算平均值与试验数据相比较为接近,说明此时自由面对螺旋桨水动力性能没有显著的影响;对于I/R=1.20、进速系数较小的情况,推力系数及转矩系数的计算平均值显著减小,说明此时自由面对螺旋桨水动力性能影响较大;计算时,没有考虑螺旋桨空化的影响, 然而I/R=4.00的数值计算结果与试验数据吻合良好,间接说明所考虑的计算工况没有出现空化现象. 表2 静水条件下的推力系数Tab.2 Thrust coefficient under the condition of calm water 表3 静水条件下的转矩系数Tab.3 Torque coefficient under the condition of calm water 图10 静水条件下的计算结果与试验数据Fig.10 Computational results and experimental data under calm water conditions 3.3.1浸水深度 为了分析浸深对波浪中螺旋桨水动力性能的影响,对一系列工况进行了计算:I/R=1.20,1.60,2.00,3.39,4.00,J=0.50,并将计算流体力学(CFD)计算结果与工程流体力学(EFD)试验数据进行比较.计算得到的推力系数及转矩系数时历曲线,如图11所示.图12给出了不同浸深比条件下的水面变形情况,水面变形越大,说明波浪对螺旋桨的水动力性能影响越大.图13给出了对应工况下的桨叶表面压力分布.可以看出,浸深比越小,螺旋桨对水面的扰动越显著;当浸深较小时,距离自由面最近的桨叶叶梢处压力最小,且叶面表面存在受到负压的区域,随着螺旋桨的浸深逐渐增大,叶面表面受到的正压也逐渐增大,受到负压的区域逐渐减小. 图11 推力系数及转矩系数时历曲线(J=0.50)Fig.11 Time history curves of thrust coefficient and torque coefficient (J=0.50) 图12 波谷处水面形态(J=0.50)Fig.12 Disturbance of free surface at wave trough (J=0.50) 图13 波谷处桨叶表面压力分布(J=0.50)Fig.13 Distribution of blade surface pressure at wave trough (J=0.50) 注意到,采用无量纲化的压力系数Cp来表示图13中螺旋桨桨叶表面的压力分布情况,其表达式为 (12) 式中:p0为静压. 从图中可以看出,I/R=1.20的推力系数及转矩系数时历曲线在部分时间段出现剧烈振荡,与其他浸深比的情况相比,呈相反的变化趋势.此时,波谷经过螺旋桨附近,导致桨叶刺穿水面,直接暴露在空气中,如图12(a)所示.暴露在空气中的桨叶无法拨水产生推力,桨叶表面的压力分布如图13(a)和图13(b) 所示,因此推力及转矩出现了剧烈振荡且减小. 表4给出了推力系数及转矩系数的计算平均值,将工况I/R=2.00,3.39的推力系数计算结果与大阪大学拖曳水池中测得的试验数据进行比较,可以看出,两种浸深比下的相对误差分别为0.94%和0.09%,计算精度较高.图14给出了推力系数平均值随浸深比变化的情况,可以观察到:螺旋桨推力随浸深比的减小而减小,且浸深比越小,螺旋桨推力减小得越快.与静水条件相比,波浪中螺旋桨推力系数及转矩系数的平均值均有减小. 表4 推力系数及转矩系数计算值(J=0.50)Tab.4 Computational results of thrust coefficient and torque coefficient (J=0.50) 图14 推力系数随浸深比的变化(J=0.50)Fig.14 Thrust coefficient versus immersion depth ratio (J=0.50) 对进速系数J=0.35的工况进行了对比分析,I/R=1.60,2.00,3.39,4.00,推力系数及转矩系数的时历曲线和计算平均值分别如图15和表5所示.推力系数随浸深比的变化如图16所示.将工况I/R=2.00,3.39 的推力系数计算结果与大阪大学拖曳水池中测得的试验数据进行比较,两者之间的相对误差分别为3.19%和4.52%.与静水条件相比,波浪中螺旋桨推力系数及转矩系数的平均值均有减小. 表5 推力系数及转矩系数计算值(J=0.35)Tab.5 Computational results of thrust coefficient and torque coefficient (J=0.35) 图15 推力系数及转矩系数时历曲线(J=0.35)Fig.15 Time history curves of thrust coefficient and torque coefficient (J=0.35) 图16 推力系数随浸深比的变化(J=0.35)Fig.16 The change of thrust coefficient with immersion depth ratio (J=0.35) 图17给出了不同浸深比条件下的水面变形情况,图18给出了对应工况下的桨叶表面压力分布.同样可以看出,浸深比越小,螺旋桨对水面的扰动越显著. 图17 波谷处水面形态(J=0.35)Fig.17 Disturbance of free surface at wave trough (J=0.35) 图18 波谷处桨叶表面压力分布(J=0.35)Fig.18 Distribution of blade surface pressure at wave trough (J=0.35) 3.3.2进速系数 为了分析进速系数对波浪中螺旋桨水动力性能的影响,对一系列工况进行了计算:J=0.20,0.35,0.50,I/R=2.00.计算得到的推力系数及转矩系数时历曲线如图19所示,可以看出:J=0.20的推力系数计算平均值与试验数据相比偏大,但两者的振荡幅度一致;J=0.50的推力系数计算平均值与试验数据更加接近,但计算所得时历曲线的振荡幅度偏大.推力系数及转矩系数的计算平均值如表6所示,将推力系数计算结果与试验数据进行比较,J=0.20,0.35,0.50的相对误差分别为5.12%、3.13%和0.94%,精度良好.进速系数越大,相对误差越小,如图20所示. 表6 推力系数及转矩系数计算值(I/R=2.00)Tab.6 Computational results of thrust coefficient and torque coefficient (I/R=2.00) 图19 推力系数及转矩系数时历曲线(I/R=2.00)Fig.19 Time history curves of thrust coefficient and torque coefficient (I/R=2.00) 图20 推力系数计算值与试验值(I/R=2.00)Fig.20 Computational results and experimental data of thrust coefficient (I/R=2.00) 当I/R=2.00且波谷经过螺旋桨附近时,水面形态与桨叶表面压力分布分别如图21和图22所示.可以观察到:当浸深比相同时,进速系数越小,螺旋桨对水面的扰动越明显,桨叶的叶面表面主要受正压,叶背表面主要受负压,且进速系数越小,叶面表面受到的正压越大. 图21 波谷处水面形态(I/R=2.00)Fig.21 Disturbance of free surface at wave trough (I/R=2.00) 图22 波谷处桨叶表面压力分布(I/R=2.00)Fig.22 Distribution of blade surface pressure at wave trough (I/R=2.00) 采用基于OpenFOAM的RANS求解器,计算了螺旋桨在静水和波浪中受到的推力及转矩,分析了浸深与进速系数对螺旋桨受力特性、水面扰动变形和桨叶压力分布的影响.通过对比分析,得出以下结论: (1) 在静水条件下,当I/R>1.60时,自由面对螺旋桨水动力性能没有显著的影响. (2) 对于存在波浪的情况,随着浸深逐渐减小,螺旋桨推力及转矩的平均值也随之减小,波浪对螺旋桨水动力性能的影响变大,当浸深较小时(I/R=1.20),桨叶会在波谷处刺穿水面,此时推力及转矩发生突变且显著减小. (3) 当浸深较小时,距离自由面最近的桨叶叶梢处压力较小,且叶面表面存在受到负压的区域,随着浸深逐渐增大,叶面表面受到的正压也逐渐增大,受到负压的区域逐渐减小. (4) 与试验数据相比,数值计算的结果精度较高,相对误差大多在5%以内.2.2 计算域与边界条件

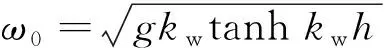

2.3 离散格式
2.4 滑移网格
3 计算结果分析
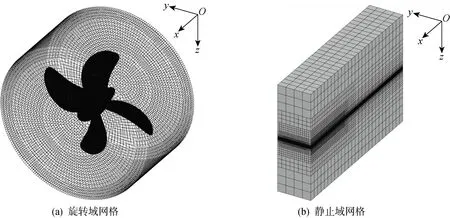
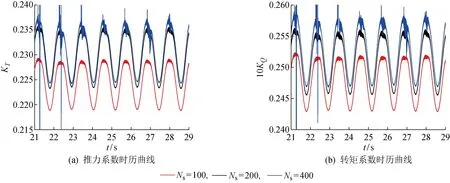
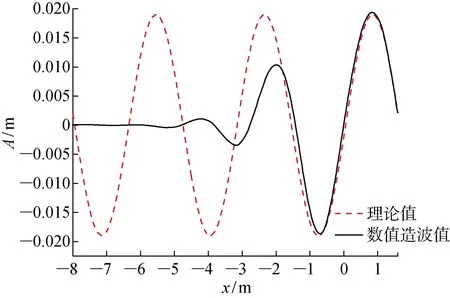
3.1 网格生成与依赖性分析
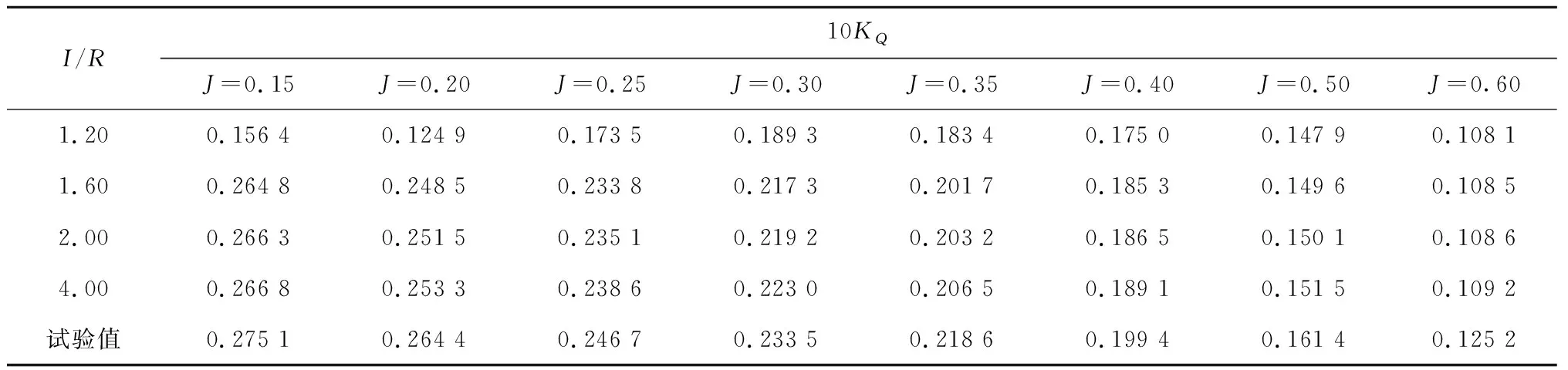
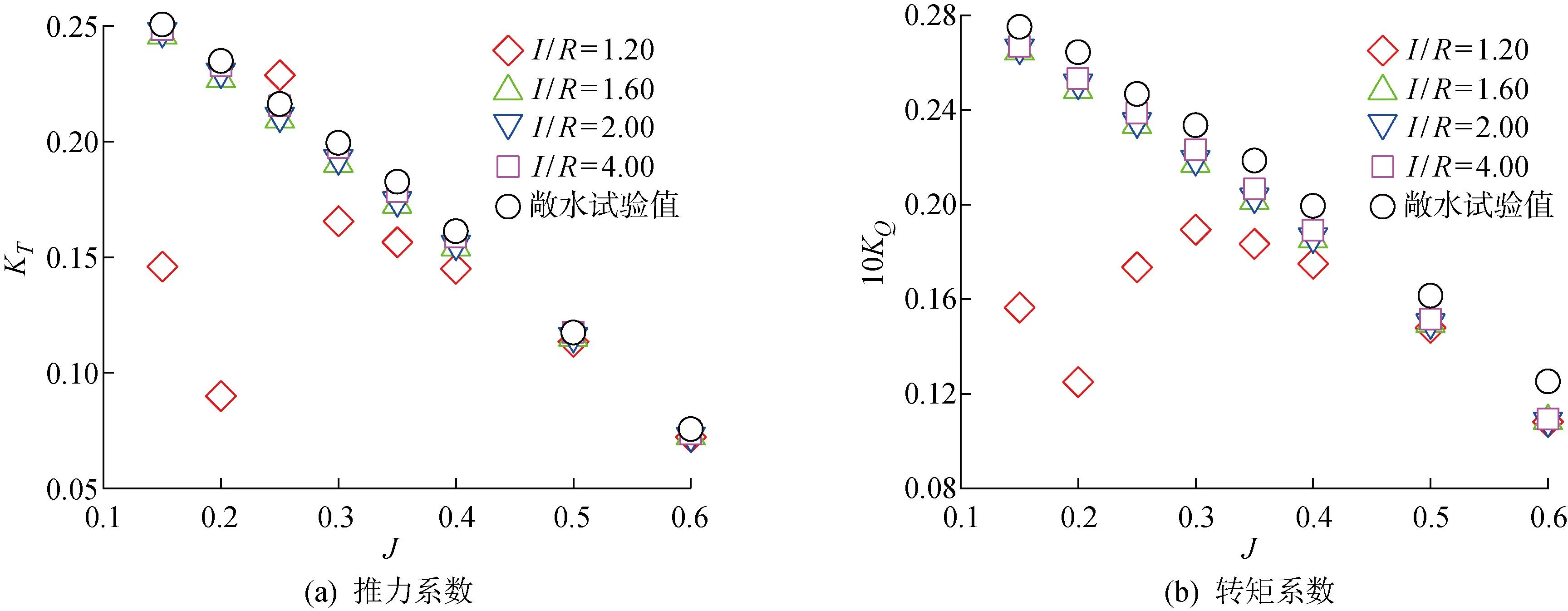
3.2 静水条件下的计算结果与分析

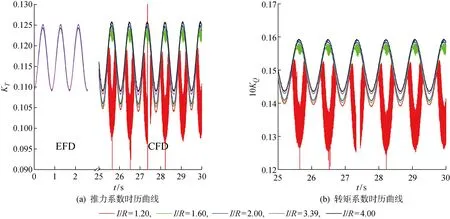
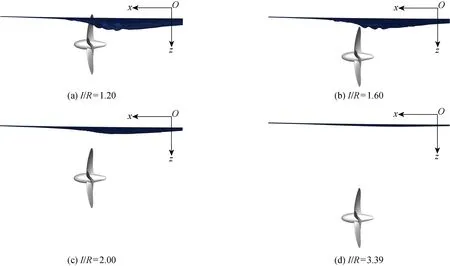
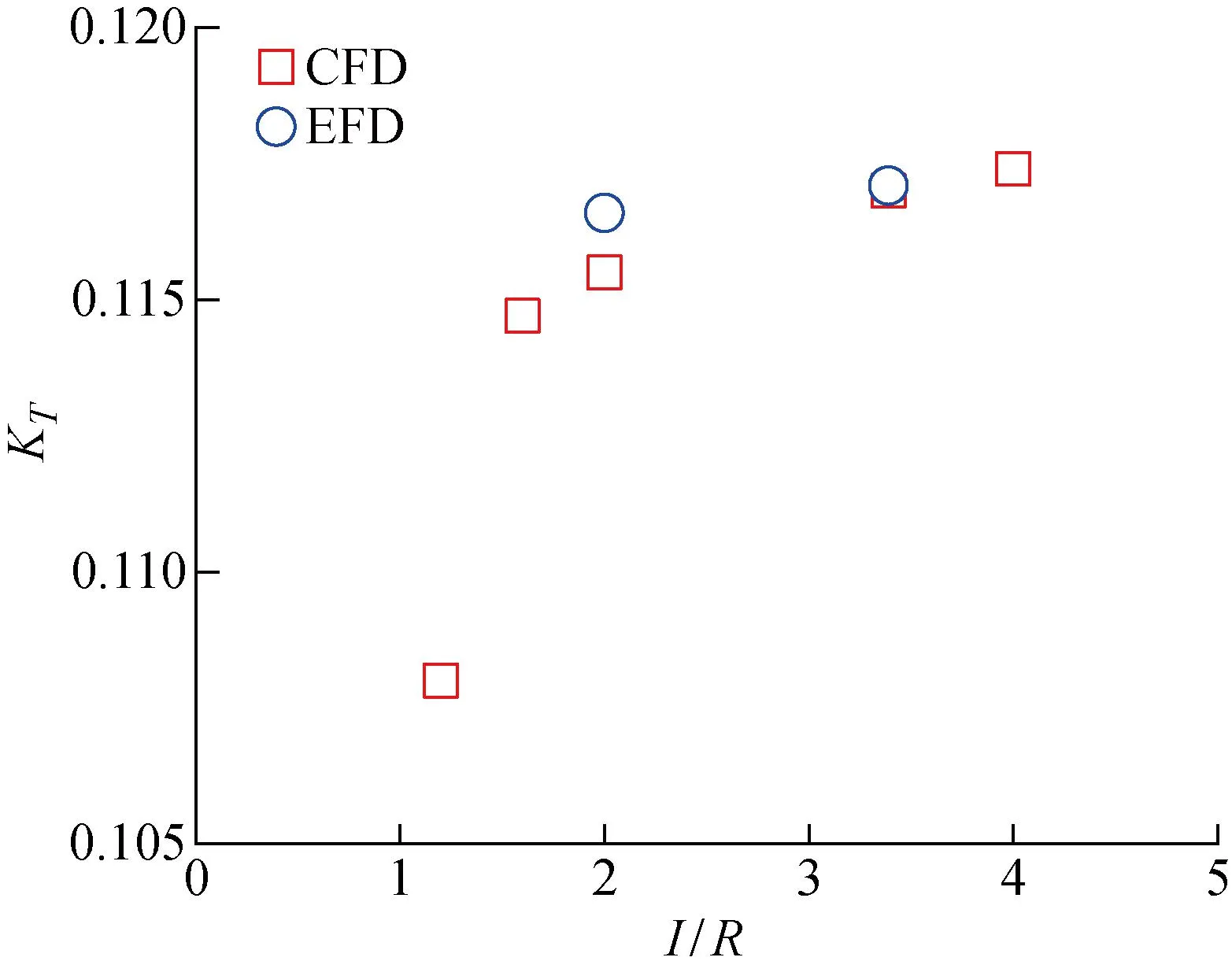
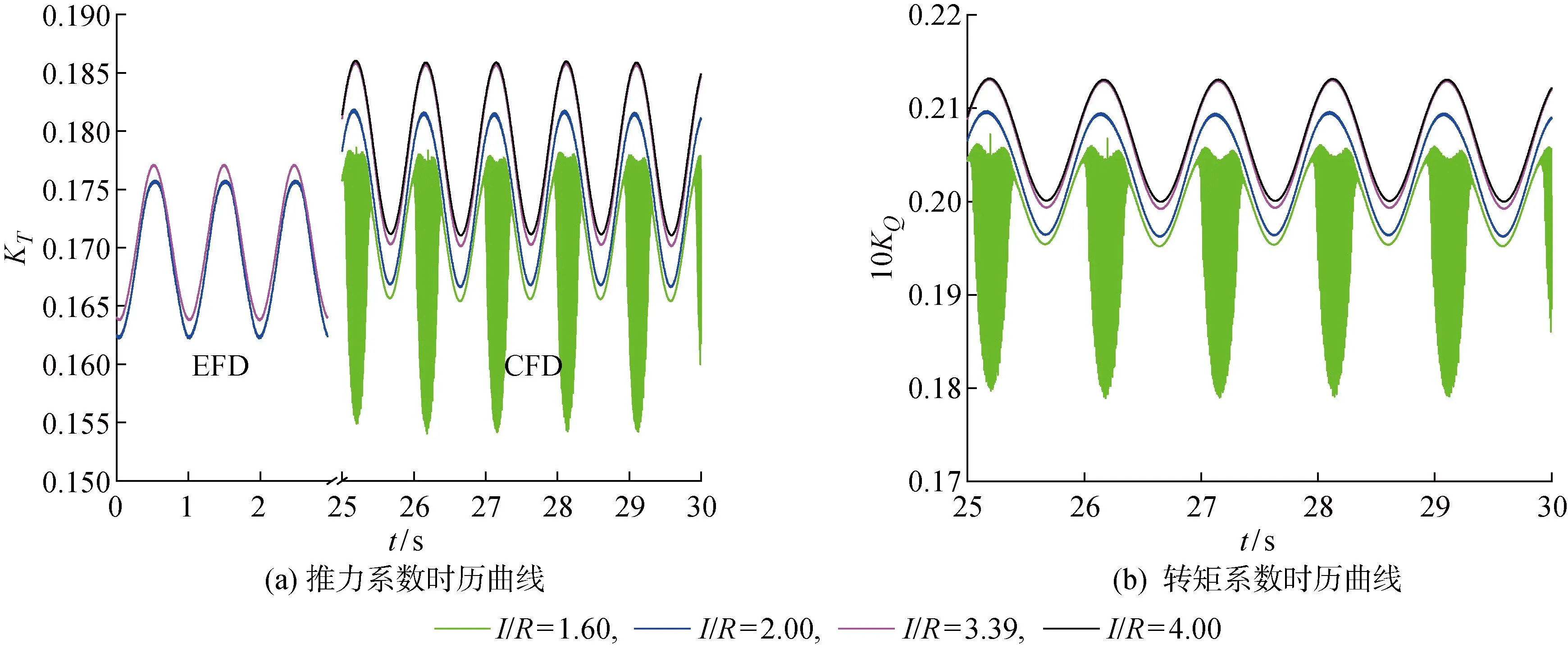
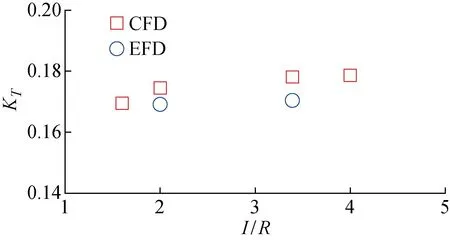
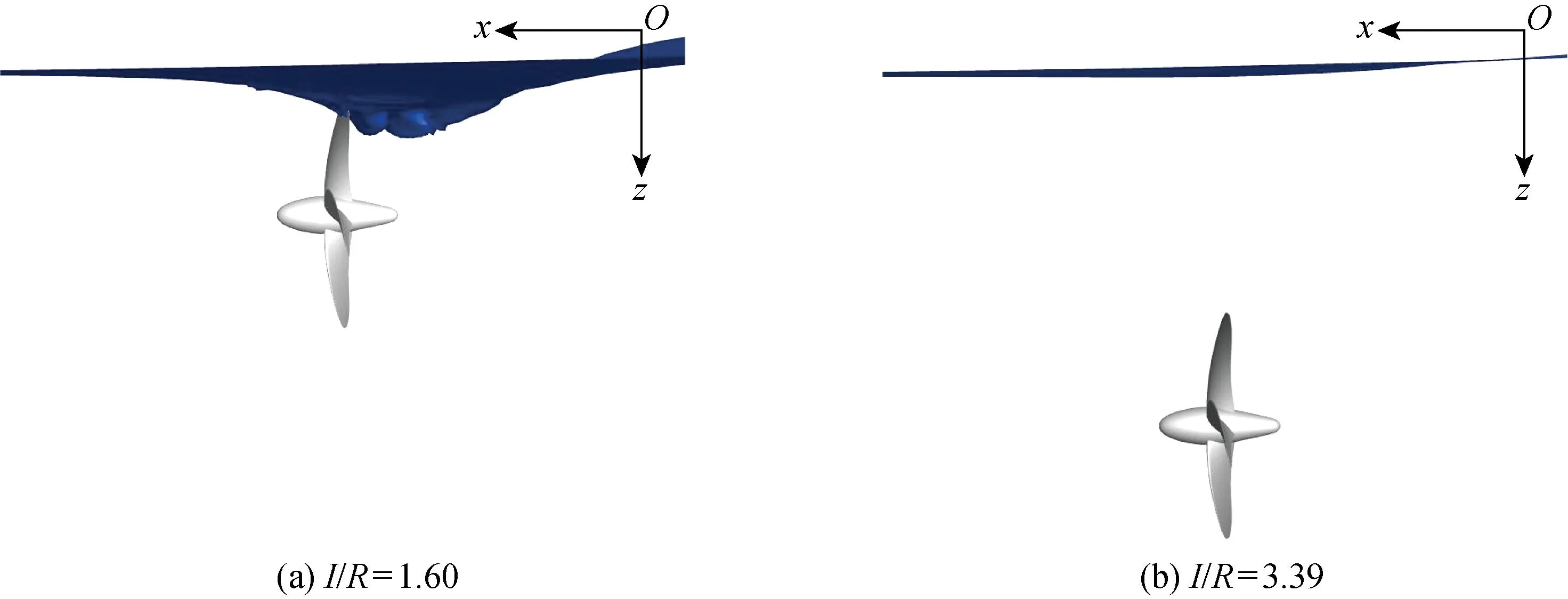
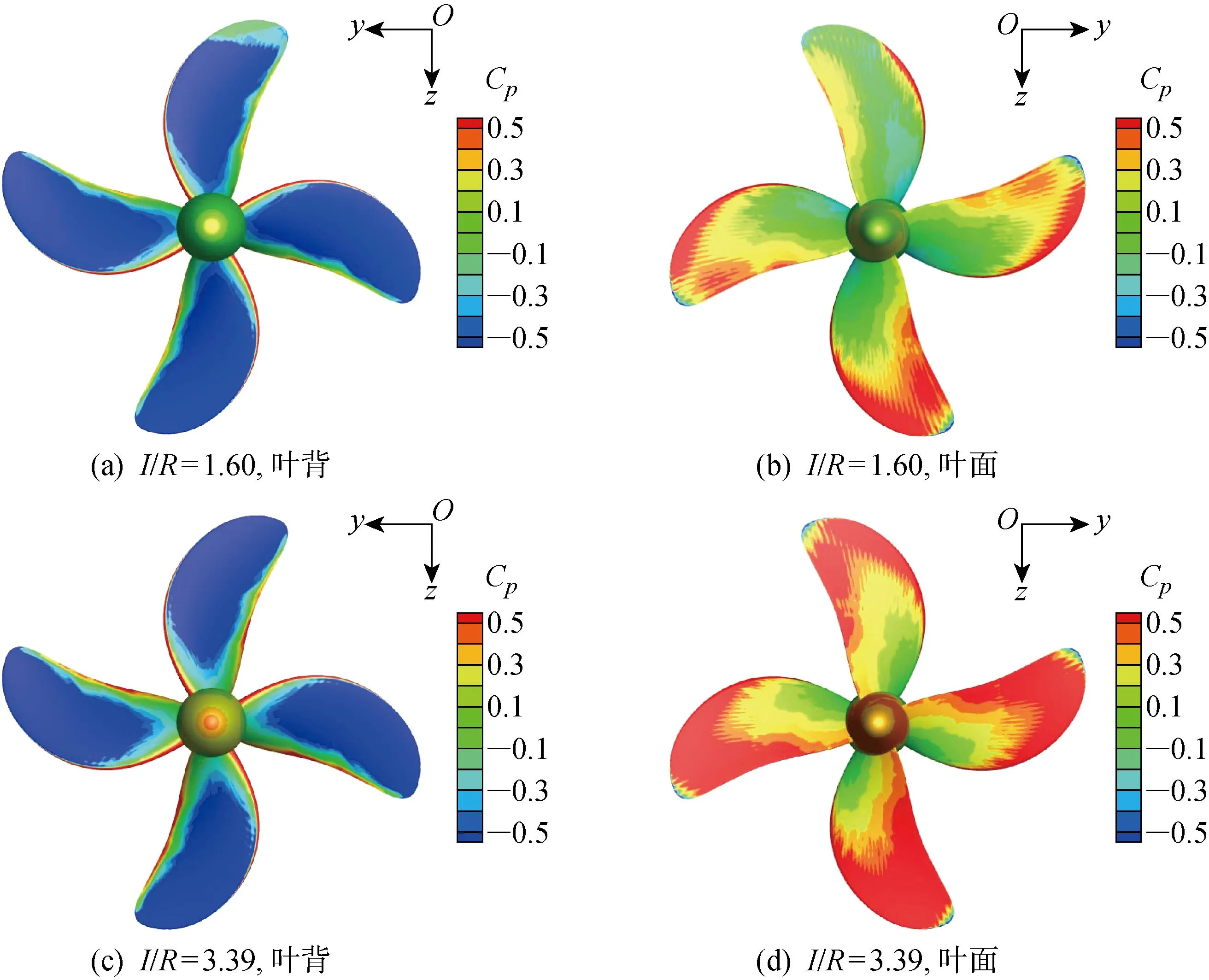
3.3 波浪中的计算结果与分析




4 结论
