STEM教育理念下初中数学项目式学习的实践探索
——以“纸张规格与的教学为例
2024-03-03沈宝松邮编361001
沈宝松 (邮编:361001)
福建省厦门双十中学
1 背景介绍
《义务教育数学课程标准(2022年版)》中提出,要让学生经历项目式学习的全过程.能综合运用数学和其他学科的知识与方法,在实际情境中发现问题,并将其转化为合理的数学问题;经过独立思考和小组合作,提出解决问题的思路,设计解决问题的方案;并能根据问题背景分析结论的意义,反思模型的合理性,最终得到符合问题背景的模型解答.
本节课是基于STEM教育理念下的初中“综合与实践”的项目式学习,能促进学生理解数学.应用数学,形成和发展学生应用意识,提升获取信息的能力、合作探究的能力、语言表达能力,感悟数学与生活、数学与其他学科的关联,发展学习能力、实践能力和创新意识.
2 教学分析
2.1 学情分析
学生已经学过二次根式,具备二次根式的基本知识和基本运算法则,为本节课的探究学习奠定了知识基础和思想理论基础.同时学生经历了二次根式、勾股定理以及四边形的学习,对几何图形的理解、实际问题的探究有更深入的了解,便于本节课的教学计划的实施.
2.2 教学目标
(1)通过探究A、B、8K等多个系列纸张的长宽比,发现比值是一个定值,并进一步思考定值产生的原因.引导学生学会在实际情境中发现问题,并将其转化为数学问题,体验数学与生活的关联.
(2)培养学生理解数学,形成和发展学生应用意识,通过材料分析提升获取信息的能力,并能用数学的语言表达实际问题,提升语言表达能力.
(3)从学生已有的生活情境出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学的理解,在思维能力、情感态度和价值观等多方面得到进步与发展.
2.3 教学重点与难点

难点:将实际问题抽象成数学问题,并用数学语言描述问题.
2.4 教学方法
本节课采用任务驱动法和小组合作学习,教师给学生布置探究性的学习任务,学生自主查阅资料,对问题进行探究,再选出小组代表进行汇报与讲解,最后由教师进行总结.
3 教学过程
3.1 探究纸张规格

图1
活动1请各学习小组展示制作的B系列的不同型号的纸张.
师生活动(1)同学展示裁剪的B系列纸张.
(2)思考这些不同大小的纸张中是否蕴藏着某些数学知识.

3.2 猜想B型纸长宽比
活动2请计算B0~B10的长宽比,并将表格填好,你能得出什么猜想?

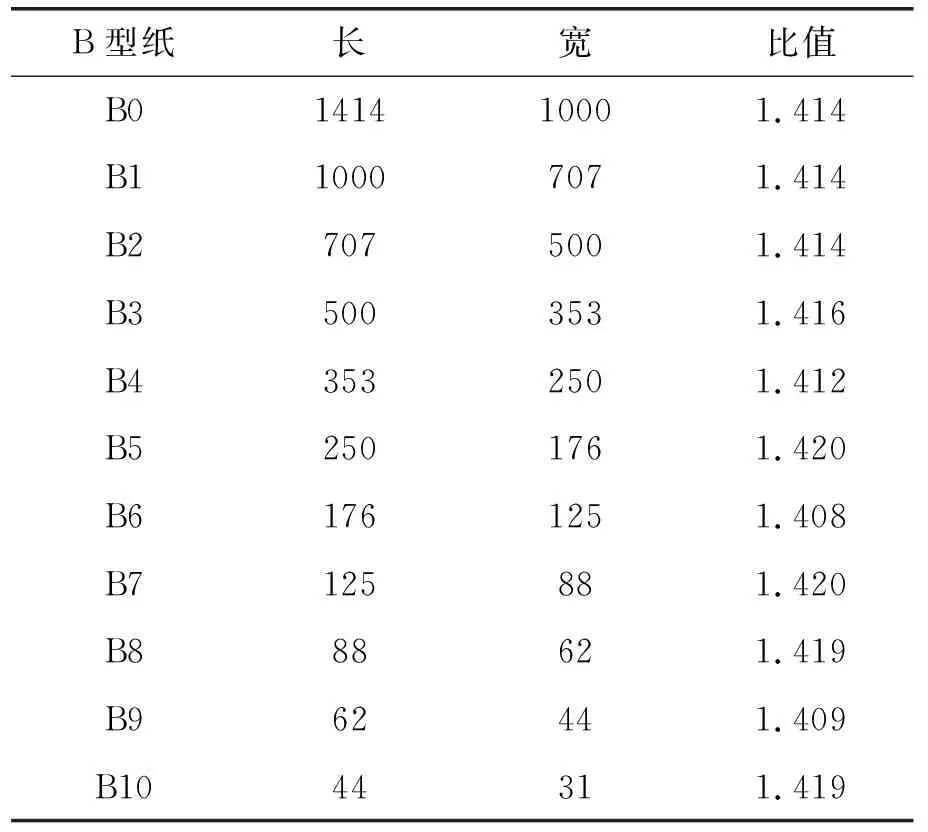
表1
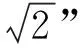
3.3 进一步猜想A型纸长宽比
活动3:我们再看一个常见的纸张类型.请同学们计算A系列的纸张长宽比值并填入表格.思考刚才的猜想是否还是成立的?
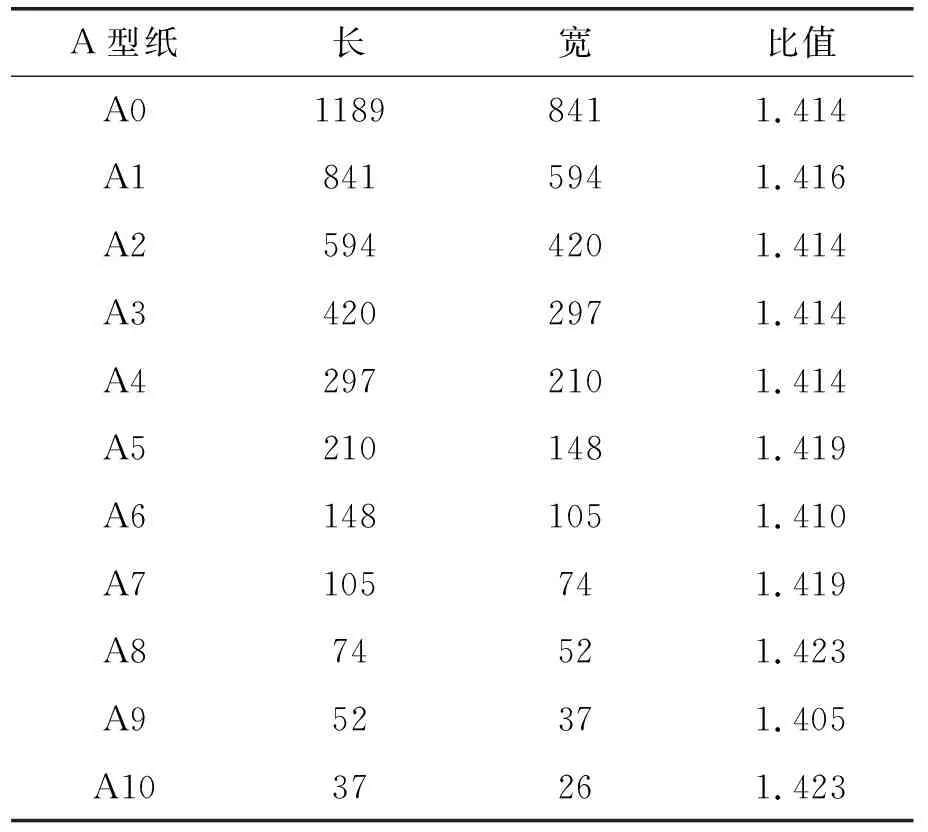
表2

师生活动学生进行计算,并发现猜想依然成立.同时引导学生思考,改变纸张的长宽比,在折叠过程中,比值是否不变,如果变化,该如何变化.
设计意图通过另一个系列—A型号的纸张长宽比计算,发现猜想依然成立.该系列中A4、A3为日常较为常见型号,能增加学生学习兴趣.在探究过程中,体验从特殊到一般的数学思想,对猜想进行举例验证,引发学生思考.在这个环节中,引导学生理解对于新问题引发的新思考、新猜想,将其应用到一般情况,让学生领悟数学的严谨性和科学性,培养学生科学探究问题的精神.该活动暂时还不进行严格证明,仅先进行举例验证.
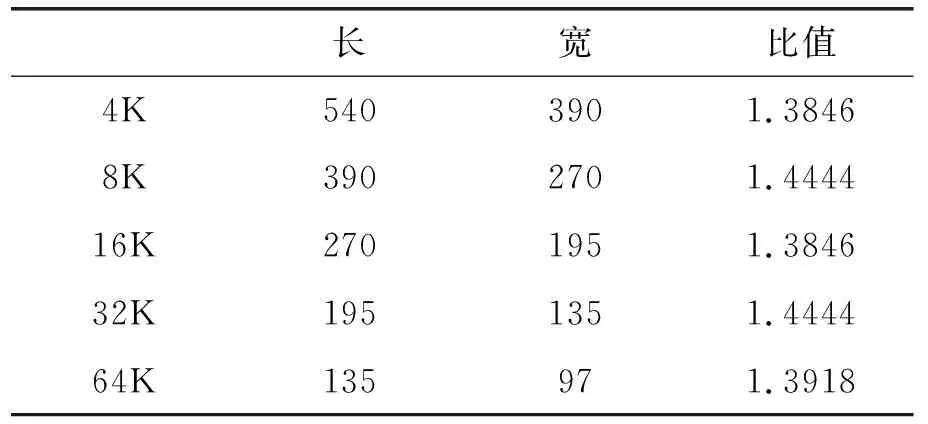
表3
3.4 进一步猜想其他类型纸张长宽比

把这张纸对折得到两张16K的纸,计算此时长与宽的比值,和刚才的比值对比,你发现了什么?
你觉得如果再次对折,比值会如何变化?动手计算看看,并提出你的猜想.
师生活动利用8K纸张进行验证,发现比值变化.

设计意图通过实际操作,发现比值变化.进一步提出,比值会如何变化?经历猜想、验证、再猜想、再验证的过程,体验数学抽象过程,形成数学能力.通过问题设置,促使学生养成多角度、多层次思考问题的习惯,培养学生直观想象素养和逻辑推理能力.在授课中,学生容易发现长宽比值发生了变化,但是要进一步地发现比值是交替出现的两个定值,是有难度的.在授课中,学生提出用正方形来进行折叠,可以更快地发现结论,这个例子更具有一般性,更有利于学生探究结论.
3.5 探究任意矩形的长宽比

表4
活动5任意一张矩形纸张,长为a,宽为b(b 设计意图通过上述几个问题的研究,逐步得出猜想,并验证猜想的正确性,培养学生数学抽象与逻辑推理素养,提高学生发现问题、解决问题的能力.也正是通过该问题的探究,培养学生善于发现生活中的数学,体会数学思想在生活中的应用. 活动6我们为什么要规定A型、B型纸中每种尺寸的纸张,长和宽的比值都相同呢?这样做的好处在哪里呢? 师生活动学生通过查阅资料,小组讨论,交流学习心得. 学生2:工业生产需要的是标准化,而1∶1.414是最适合于标准化纸张型号的比例,以A0到A6这个区间来说,A0=841×1189mm面积正好是1平方米,不断将长边对折分割并且不会改变原来的比例关系,而且在大量的生产过程中不会造成任何的纸张浪费. 学生3:生活中有很多物品的尺寸不仅仅是依靠人们的经验制定的,更多的是利用数学方法计算出更加合适的标准,形成行业标准,进一步推动人类社会的进步. 设计意图将数学内化成为自己的思维,这也正是数学的学科意义所在.善于从实际生活中抽象出数学模型,从已知领域到未知领域的探索,让思维实现质的飞跃.我们要用数学的眼光去观察,用数学的思维去思考,一定会有别样的收获. 基于STEM教育理念下的初中“综合与实践”项目式学习,强调数学学科与学生校园生活、家庭生活和社会生活相关联的内容,这些内容是当数学的图形、数量关系、结构、空间形式和其他学科以及生活经验发生联系时产生的研究型内容.综合与实践只有跳出数学本身的狭窄范畴,教学内容才能得到有效扩充.同时,数学的理性和准确性对项目式学习的方向、广度、深度有着决定性的作用. (1)从实际问题抽象出数学问题 (2)用数学思维解决数学问题 在该课中,主要是以数学的思想方法为跳板,借用数学计算工具和生活经验,经历分工合作、建立模型、计算反思、解决问题的过程,用数学的概念、定理或者公式予以表达,凸显数学应用的价值,促进学生思维能力的培养,逐步形成“会用数学的思维思考现实世界”的核心素养. (3)用数学语言表达实际问题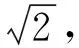
3.6 交流学习心得

4 教学反思
