数学运算素养的高考测评比较研究——以2021—2023年新高考Ⅰ卷、Ⅱ卷和全国甲卷为例

丁红艳 杨晓丹 (邮编:550025)

贵州师范大学数学科学学院

随着新课改的不断推进,数学核心素养成为了当代数学教育家研究的热点话题之一.2014年,教育部颁布的《关于全面深化课程改革落实立德树人根本任务的意见》中明确提出建立核心素养体系[1].2018年,教育部颁布的《普通高中数学课程标准(2017年版)》中提出了六大数学核心素养,即数学抽象、逻辑推理、数学建模、直观想象、数学建模和数据分析[2].近年来,研究者从不同角度、不同领域对数学核心素养进行了大量的研究,其中朱立明、喻平、胡典顺、王尚志等是数学核心素养的主要贡献者.如朱立明在《高中数学教学类型的理论探析:数学学科核心素养视角》中基于数学学科核心素养提出了数学教学类型划分的三个研究视角[3];喻平在《数学核心素养评价的一个框架》中将数学核心素养划分为三个水平:知识理解、知识迁移和知识创新[4];胡典顺在《数学教与学、数学动机及知识熟悉程度对数学核心素养的影响》中运用定量分析的方法说明了学生的学、教师的教、数学动机、知识熟悉程度对数学核心素养均存在显著的影响作用[5],可见数学核心素养在数学教学中的重要地位.经过文献的整理分析发现,研究者更倾向于对数学核心素养整体进行研究,就某个核心素养的研究较少.数学运算素养作为六大核心素养之一,而高考是检验高中学生数学学习成果的重大考试, 因此文章将基于数学建模素养,参照喻平教授对数学核心素养的评价框架,以2021～2023年新高考Ⅰ卷、Ⅱ卷和全国甲卷(理科数学)为例进行测评研究.

1 研究设计

1.1 评价框架

基于《普通高中数学新课程标准(2017年版)》,参考喻平教授制定的核心素养评价框架中划分的三个水平,即知识理解、知识迁移、知识创新[4],对高考数学试题中的数学运算考查情况作针对性的分析,根据本文研究需要,将数学运算素养评价框架及水平划分调整如表1.

表1 数学运算素养不同水平的要求

1.2 试题编码

(1)对试题的量化计数

根据高考数学试题的划分,考查形式涉及选择题、填空题、解答题,由于解答题中会有2～3个小题,因此采用小题计数的方法对2021～2023年新高考1、Ⅱ卷和全国甲卷(理科数学)9套试卷中涉及运算素养的题目数量及分值进行统计.由于全国甲卷包含选做题2道(只做1道),为使统计结果更加准确,三类试卷均选择第22题进行编码.

(2)试题评价指标量化过程

按照喻平教授对核心素养的评价框架进行统计,并运用加权平均值的算法,统计数学运算素养各水平的均值,以此衡量其考查程度.为使结果更加准确,对9套试卷进行多人编码统计,经过讨论,最终获得相对一致的结果.具体方法为:对各个水平进行赋值,若题目没有考查数学运算,则赋值为1,在考查数学运算的情况下,考查知识理解水平,赋值为2;考查知识迁移水平,赋值为3;考查知识创新水平,赋值为4,用字母分别表示为C1,C2,C3,C4,见表1,计算公式如下:

其中d表示数学运算水平的加权平均值,ni表示试题中属于数学运算素养中的第i个水平的数量,其总数和等于试题总数.di表示数学运算素养在第i个水平上的权重.

(3)例题分析

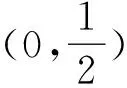
(i)求W的方程;

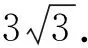
该题考查了数学运算素养,第一问为基础题,主要考查两点间距离公式,只要学生熟记公式,便可进行解答,运算过程相对简单,因此属于知识理解水平,赋值为2.第二问包含的知识点较为综合,涉及导数、函数的单调性、函数的对称性、直线方程与抛物线方程公式及特征、求最值等知识点,并且运算过程复杂,需要学生合理选择运算方法,该题的关键是学生能利用放缩法求最值,对学生的思维层次和运算能力较高,因此属于知识迁移水平,赋值为3.

2 研究结果与分析

2.1 数学运算素养考查试题信息汇总

经过数据整理,得到三类试卷在数学运算素养各个水平上的试题考查数量统计,见表2.

表2 数学运算素养各个水平的考查情况

2.2 数学运算素养的考查情况比较研究

(1)数学运算素养的直观比较

统计结果见图1,2021～2023年共九套试卷的样本中,新高考Ⅰ卷、Ⅱ卷、全国甲卷都比较注重数学运算素养的考查,没有考查数学运算素养的题目分别占3.53%、 5.75%、4.82%.考查数学运算素养的题目中,三套试卷都比较注重对知识理解和知识迁移水平的考查,属于知识理解水平的题目分别占32.94%、42.53%和55.42%,占比最高的是全国甲卷,新高考Ⅰ卷占比最低,说明新高考Ⅰ卷最重视对知识的理解.属于知识迁移水平的题目分为占56.47%、41.38%和38.55%,占比最高的是新高考Ⅰ卷,最低的是全国甲卷,说明新高考Ⅰ卷对知识的迁移最为重视.属于知识创新水平的题目分别占7.06%、10.34%和2.41%,占比最高的是新高考Ⅱ卷,最低的是全国甲卷,说明新高考Ⅱ卷比较重视学生学会运用运算结果解释数学现实问题及其创新应用,但整体上看三类试卷对知识创新的考查比重较低.

图1 数学运算素养考查占比

(2)数学运算素养考查程度比较

运用加权平均值公式,得到结果如图2所示,三类试卷对数学运算素养的考查程度分别为2.67、2.46和2.39.考查程度最高的是新高考Ⅰ卷,最低的是全国甲卷.

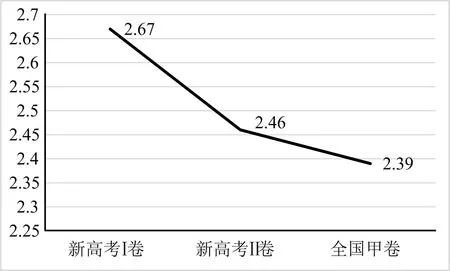
图2 加权平均值

(3)数学运算素养的卡方检验

为了进一步比较三类试卷数学运算素养之间的差异性,运用SPSS26.0软件对频数加权后再进行卡方检验,结果见表3,皮尔逊卡方检验的显著性p=0.043,p<0.05,说明新高考Ⅰ卷、新高考Ⅱ卷和全国甲卷之间具有显著性差异.

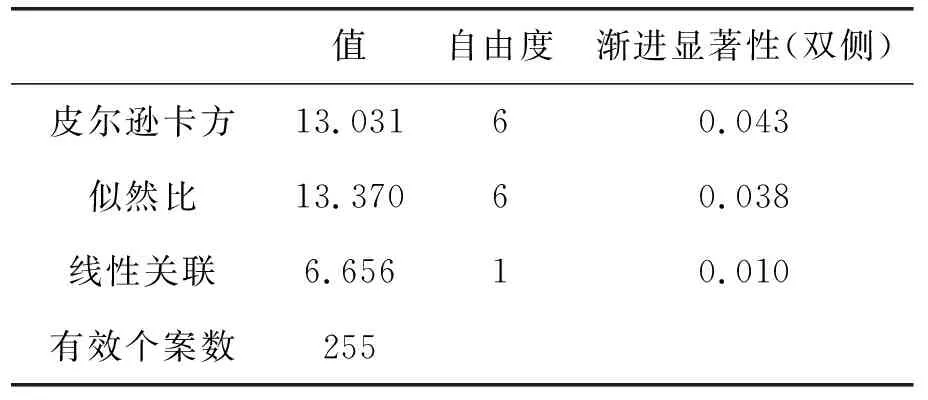
表3 新高考Ⅰ卷、新高考Ⅱ卷和全国甲卷卡方检验

为具体确定哪两类试卷之间存在显著性差异,对多组间进行两两比较,卡方检验时调整p值(邦弗伦尼法)[6].

由表4可知,皮尔逊卡方检验的显著性p=0.257,p>0.05,说明新高考Ⅰ卷和新高考Ⅱ卷之间不具有显著性差异.

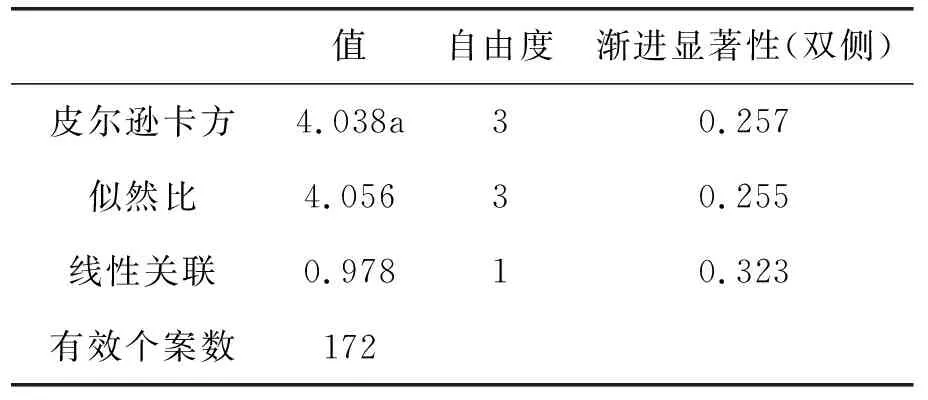
表4 新高考Ⅰ卷和新高考Ⅱ卷卡方检验

由表5可知,皮尔逊卡方检验的显著性p=0.108,p>0.05,说明新高考Ⅱ卷和全国甲卷之间不存在显著性差异.

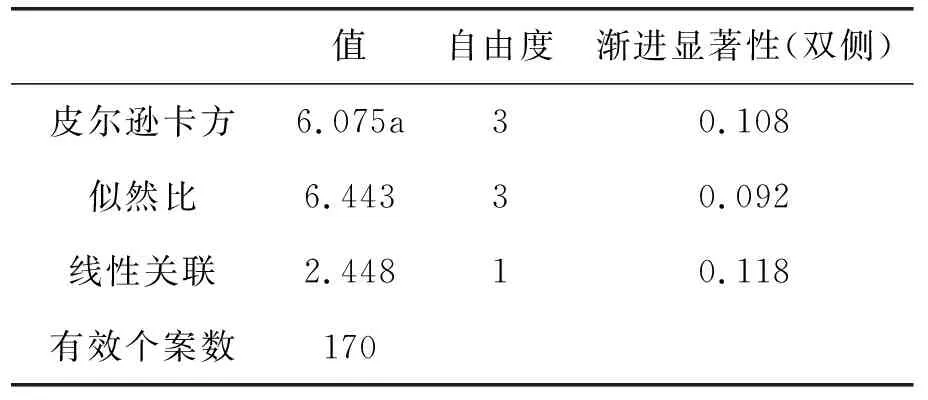
表5 新高考Ⅱ卷和全国甲卷卡方检验

由表6可知,皮尔逊卡方检验的显著性p=0.023,p<0.05,可认为新高考Ⅰ卷与全国甲卷之间具有显著性差异.

表6 新高考Ⅰ卷和全国甲卷卡方检验

(4)数学运算素养的对应分析

为分析三类试卷的分布特征和分散距离,运用SPSS26.0对数据进行对应分析[7].由图3所示,整体上看,新高考Ⅰ卷、新高考Ⅱ卷和全国甲卷在空间上呈分散状态,三类试卷在维度1和维度2上均与原点的距离相差较大,说明三类试卷对数学运算素养考查程度区别较大,命题特点各不相同,与上文的卡方检验结果一致.从各类试卷的考查特征看,全国甲卷离知识理解水平较近,其更注重对知识理解的考查;新高考Ⅰ卷离知识迁移水平较近,其更注重学生对知识迁移能力的考查;在知识创新水平方面,而新高考Ⅱ卷离得更近,相对于其他两套试卷,其更注重开发学生的创新意识.

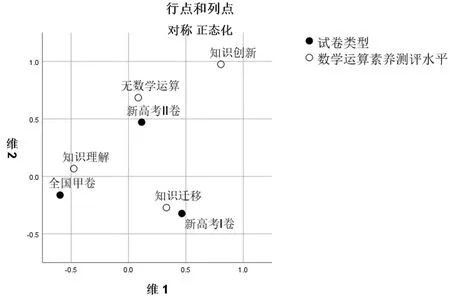
图3 对应分析

3 研究结论与建议

3.1 结论

根据上述研究,在数学运算素养的考查方面,直观上,三类试卷都比较注重对知识理解和知识迁移水平的考查,对知识创新水平考查程度较低.从加权平均值结果来看,新高考Ⅰ卷的考查程度最深,全国甲卷最低.经过卡方检验,发现三类试卷之间存在显著性差异,两两比较后,得出具有显著性差异的是新高考Ⅰ卷和全国甲卷.进一步运用对应分析方法,得出全国甲卷更关注对知识理解水平的考查,新高考Ⅰ卷更重视对知识迁移水平的考查,而新高考Ⅱ卷对知识理解和知识迁移水平的考查相差不大,但在创新水平上,相对于其他两类试卷,新高考Ⅱ卷更注重对知识创新水平的考查,说明其命题趋势逐渐转为考查学生的创新能力.

3.2 教学建议

(1)培养学生良好的运算习惯

通过上文对新高考Ⅰ卷、新高考Ⅱ和全国甲卷的直观分析,高考数学试卷大部分的题目都有考查数学运算核心素养,可见学生具备数学运算能力的重要性.而形成良好的运算习惯对于提升学生的数学运算核心素养具有重要作用[8],如学生在解题过程中时常因为没有仔细审题、计算粗心、书写混乱等导致解题错误,因此,教师在教学时,应该培养学生仔细审题、计算仔细、书写整齐等习惯,有利于培养学生的数学运算核心素养,同时也能提升数学成绩.

(2)加强对学生逻辑推理能力的培养

根据上述研究,三类试卷对数学运算素养知识迁移水平的考查比重较大,可见高考对学生知识迁移能力的重视.学生合理运用正确的迁移方法是正确解题的关键,在解题过程中,选择哪一种运算方法则体现的是学生的逻辑思维能力,若学生的逻辑混乱,将无法得出正确答案.逻辑推理是六大核心素养之一,《普通高中数学课程标准(2017年版2020修订)》指出逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证[9].因此,教师在教学过程中应重视学生逻辑推理能力的培养,可通过活动交流、信息技术、问题提出等的教学方式提升学生的直觉感知,培养学生的学习兴趣,使其能对知识进行推理,深度掌握数学知识.

(3)加强对学生创新意识的培养

2019年,教育部考试中心明确提出了“一核”“四层”“四翼”的中国高考评价体系,其中要求高考题目设置要具有创新性[10].从上文对三类试卷的直观分析发现,新高考Ⅱ卷的题目逐渐向创新方面发展,意在考查学生灵活运用知识的能力,可见创新性题目未来高考的一个命题趋势.因此,教师在日常教学过程中,应采取灵活有效的教学方式、更新自身的教学理念,加强对学生创新意识的培养.