基于学生问题意识培养的初中数学教学探索

陆青

当下，部分教师会关注学生分析和解决问题的能力的培养，却忽视了培养学生发现问题和提出问题的能力。一味强化学生分析和解决数学问题的能力，很难让学生达到“用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界”，所以，初中数学的课堂教学应该关注学生发现问题的意识及能力的培养，而问题意识的培养是学生提出问题的前提。下面，笔者以“图形的旋转”复习课为例，谈谈对基于问题意识培养的教学实践的探索。

一、设计理念

平移、旋转和翻折是几何变换中的三种基本变换，九年级学生对此已充分了解。笔者从三个方面进行思考，以更大程度地培养学生的问题意识，增强学生的空间观念和推理能力。一是问题意识的引导。学生在面对某一学习对象的时候，如果能够自发地产生问题，也就意味着引导成功了。所以，教学要以容易激发学生兴趣的情境或问题导入，让学生产生迫切探究的欲望，为问题意识的产生做足准备。二是问题冲突的呈现。教师要在教学设计中创设足够的探究空间，供学生自由思考和表达。三是问题解决的深化。问题设计要有“闭环”意识，通过开放性问题的设计，不断分析、解决同一情境下的不同问题，或者从不同角度解决同一问题，寻找“变”中的“不变”。

二、教学片段

1. 情境引入（问题意识的引导）

师：如图1所示，静止汽车的雨刮器在转动时，你能找到雨刮器上的雨刷AB，绕着点O逆时针旋转45°后的雨刷A′B′的位置吗？

生：将雨刷看成一条线段AB，点O看成旋转中心（图2），作出线段AB关于点O逆时针旋转45°后所得的线段。

师：很好，这就是一个基本的旋转作图。哪位同学为我们演示一下作图的步骤？

学生在黑板上演示作图（图3），讲解作图步骤。

师：在这个变换中，你能得到哪些结论？

生：0A=0A′，OB=OB′，AB=A′B′，∠A0A′=∠BOB′。

师：旋转的性质有哪些？

生：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角相等且都等于旋转角；旋转前后的图形全等。

师：你还能得到其他结论吗？

生：∠AOB=A′OB′。

师：旋转是一种全等变换，它只改变了图形的位置，所以旋转变换会产生很多相等的边、相等的角、相等的线段。

【设计意图】通过实际问题，思考画旋转图形的方法、旋转的本质、旋转后的结论，为后续的问题呈现和问题深化提供实践基础。

2. 自主探究（问题冲突的呈现）

师：旋转在生活中应用广泛，在数学中是解决平面几何问题的重要工具之一，其看似简单的变换可以产生很多复杂的问题，下面我们就从矩形的旋转开始探究。

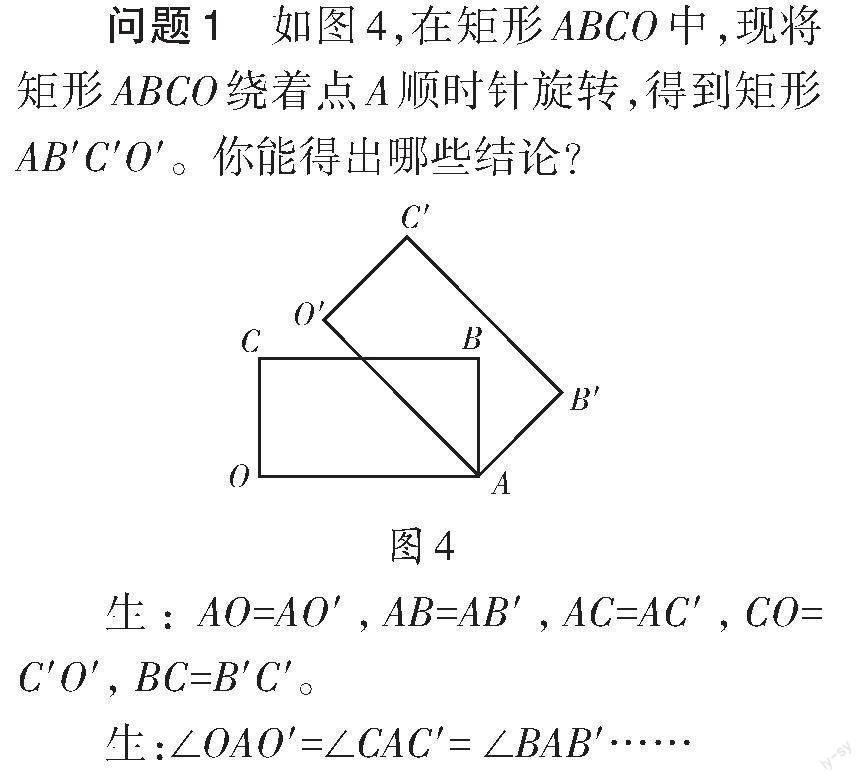
问题1 如图4，在矩形ABCO中，现将矩形ABCO绕着点A顺时针旋转，得到矩形AB′C′O′。你能得出哪些结论？

生： AO=AO′，AB=AB′，AC=AC′，CO=C′O′， BC=B′C′。

生：∠OAO′=∠CAC′= ∠BAB′……

师：除了全等、相等的线段和相等的角，还有其他结论吗？大家可以进行讨论交流。

生：我发现，△CAC′、△OAO′、△BAB′相似。

生：通过相似还可以得到比值关系，CC′[∶]OO′[∶]BB′=AC[∶]AO[∶]AB。

师：你还有什么发现？

生：在图形变换的过程中，有些关系、有些值是不变的。

【设计意图】教师创设宽松和谐的课堂氛围，逐步增强学生的自信心，给予学生独立发现的时间，引导学生提出富有价值的问题。问题的呈现让学生充分暴露自己的认知，并更加准确地描述和表达自己的认知。当不同的学生带着不同的观点参与课堂活动时，在该环节，学生慢慢发现旋转的不变性。在这个逐步递进的过程中，教师应当充分利用好合作学习这个环节，让学生在和谐的氛围中表达自己的观点。此时，问题意识的激活与深化起到了关键的作用。

3.变式训练（问题解决的深化）

问题2 如图5，在矩形ABCO中，点B的坐标为（8，4），现将矩形ABCO绕着点A顺时针旋转，得到矩形AB′C′O′。你能提出哪些问题？并尝试解决问题。

生：可以求BB'与CC'的比值。

生：可以求OB′、OC′的范围。

生：可以求旋转45°后O′、B′、C′的坐标。

生：可以求图形面积。

……

师：大家在设计问题、解决问题的过程中，有没有什么发现或想法呢？

生：解决旋转问题的根本是抓住变中的不变性。

【设计意图】学生提问，学生解决，学生在智慧碰撞中，发现解决旋转问题的根本是抓住旋转不变性。从发现、提出问题，到分析、解决问题，都由学生主导。随后，教师可引导学生总结、归纳其中的思想方法，挖掘其本质。

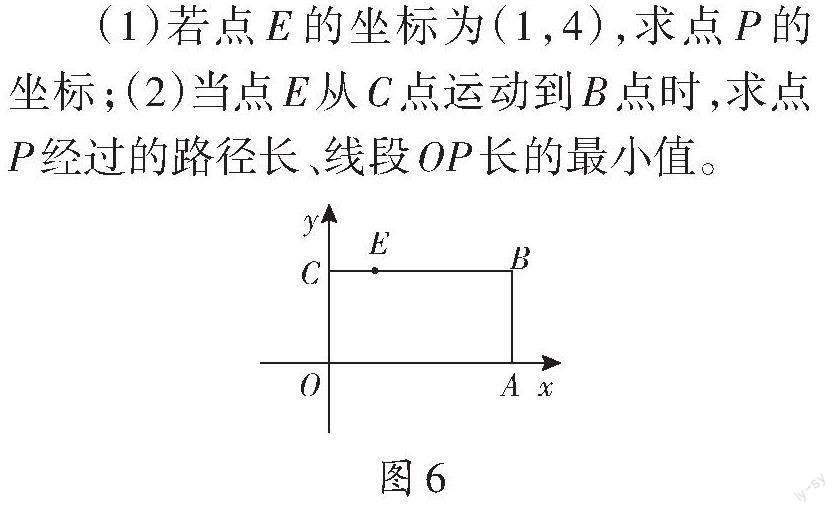
问题3 如图6，在矩形ABCO中，点B坐标为（8，4），点E是线段CB上一动点，以点E为旋转中心，把线段EA绕点E逆时针旋转90[°]，点A的对应点为点P。

（1）若点E的坐标为（1，4），求点P的坐标；（2）当点E从C点运动到B点时，求点P经过的路径长、线段OP长的最小值。

4. 总结反思

最后，教师引导学生从这几个方面进行总结：如何研究图形的旋转？关于图形的旋转主要研究哪些问题？怎样进行研究？研究图形旋转时要注意采取哪些思想方法？类比图形的选择，在解决图形的变换的问题时，你有哪些想法？

【设计意图】旋转中心由定到动进行变化，学生在分析过程中，发现解决旋转问题的根本仍是抓住不变性，同时发现可以用函数的思想解决问题。该问题的设计促成了问题教学的“闭环”。通过问题3，了解学生的学习情况，本节课达成了预期效果。最后的总结反思帮助学生进一步梳理、完善和强化所学习的知识，也对问题的解决进行最后的深化。

三、教学反思

数学学习必须有问题，没有问题无法学好数学。在学习过程中，打破惯性思维和惰性思维，进行不断质疑产生的新思想才是学生真正的收获。在此过程中，学生的创新意识也在加强，所以，创新教育实际上是以培养学生问题意识作为起点的。

本节课，笔者从日常的汽车雨刮器的转动情境中，引导学生用数学的眼光观察世界。学生在自主思考中復习了画旋转图形的方法、旋转的本质、关于旋转的结论。通过没有条件的旋转能得到哪些结论？学生自由思考。每个学生都是从自身的已有知识经验和生活经验出发理解新事物的，因此，不同学生对于同一个情境可以提出不同的问题。当学生的思维自由发散时，他们原有的知识和经验与新的学习内容之间就很容易发生“冲突”，这个“冲突”就是问题形成的基础。如果让学生产生兴趣是问题教学开展的前提，那么让学生自由呈现“冲突”和问题则是问题教学的关键。一题多变、 一题多解可以帮助学生呈现对同一问题的不同思考。学生在各种“冲突”中，通过研究，关注到旋转的不变性，发现了解决旋转问题的根本是抓住旋转不变性，哪怕旋转中心由定到动变化，解决旋转问题的根本仍是抓住不变性。通过对问题的“闭环”设计，深化对问题的思考和研究；通过对“冲突”的分析和总结，提炼解决问题的思想和方法。

本文系江苏省南京市教育科学“十四五”规划课题“指向核心素养的初中数学问题教学实践研究”（课题编号：JZ/2021/058）阶段性研究成果。

（作者单位：南京师范大学附属中学江宁分校）