基于认知状态的互补均衡聚类分组模型研究

王彬彬，李 强

人工智能和数据挖掘技术在教育领域的应用已取得阶段性成果［1］.教育领域已采集并存储了海量的数据，针对数据的分析，人们也提出了大量的算法与模型［2−7］.数据驱动的协作学习已成为重要的研究方向［2］，在教育数据挖掘领域得到了广泛关注.

目前基于聚类的分组方法使用样本间的距离进行相似度分析［5−6］，在应用中主要有三方面的挑战：一是聚类方法容易导致不均衡的划分；二是聚类方法产生的是同质分组，相似的学生被划分在一起，不利于实现能力互补的协作学习；三是现有的分组方法对学生的学习能力进行评估时，主要通过问卷或者人工标注的方式，量化不充分.

为了解决目前分组中存在的不足，设计了一种基于知识互补的学生分组模型，通过认知诊断对学生知识状态进行量化之后，使用一种改进的均衡聚类算法对学生进行分组.对比实验验证了该算法能够有效提升分组的知识互补与均衡.

1 认知状态特征表示

互补均衡分组方法的执行过程如图1 所示.首先需要依据认知诊断模型，估计出学生的认知状态，量化学生的知识点掌握情况.然后使用改进后的均衡聚类算法，依据学生的认知状态进行聚类，将认知相似的学生聚到相同的簇中.最后依据组内知识互补、组间知识均衡的分组目标，将聚簇中的学生分配到每个小组中，获得最终的分组方案.

图1 分组流程示意图

认知状态是学生知识水平和认知结构的量化体现，应用于众多教育数据挖掘领域.在广泛使用的DINA、rRUM 等认知诊断模型中，认知状态通常使用二分向量αi=[αi，1，αi，2，…，αi，t，…，αi，T]进行表示.其中，模型共包括T个知识点，αi表示第i个学生的认知状态，αi，t表示学生i对第t个知识点的掌握状态.αi，t=1，表示学生i掌握了第t个知识点，反之，αi，t=0，则表示学生i未掌握第t个知识点.表1 给出了两个学生认知状态示例，学生1 的认知状态可以表示为α1=[ 1，0，1，1，0 ]，学生2 的认知状态可以表示为α2=[ 1，1，0，0，1] .

表1 学生认知状态示例

通过认知诊断模型，可以精确地获得学生的量化认知状态特征，之后便可以基于学生的认知状态进行协作学习分组，达到组内学生知识更为互补、组间总体知识更为均衡的效果，进而提升协作学习的效率.

2 互补均衡聚类分组模型

2.1 分组目标定义

知识互补是指学生之间通过相互学习，从对方身上学到自身未掌握知识的过程.显然学生之间掌握的知识差异越大，能从对方身上学习到的知识越多，学生之间的知识互补程度越高，因此可以通过学生之间掌握的知识差异程度来衡量学生之间的知识互补程度.学生p和学生q之间的知识互补率d(p，q)可以定义为：

知识点总数为T，当学生p和学生q都掌握或都未掌握知识点t时此时学生p和学生q无法在知识点t上进行互补.而如果则表示学生p和学生q中有一名学生掌握了知识点t，另外一名学生可以通过知识互补学习到知识点t.显然d(p，q)的值越大，表示学生p和学生q的知识互补程度越高.

对于包含多名学生的小组来说，小组的知识互补率u(gj)可以用两两学生的知识互补率均值表示：

其中：gj={gj，1，gj，2，…}表示小组j中包含的学生集合，zj表示第j组中学生的数量，表示两两学生组合的个数.显然，u(gj)的值越大，表示小组的整体知识互补程度越高，即两两学生相互学习的帮助越大.

对于包含多个分组的分组方案，分组方案的整体知识互补率U，可以用分组方案中所有小组（分组数量M）的知识互补率均值表示.

U越大，代表分组方案中，各小组的知识互补程度越高，越有助于小组成员间的相互学习.然而在进行分组时，除了要考虑组内的知识互补度，还要考虑组间的知识均衡度.组间知识水平差异过大，会造成不同小组成员成绩分化严重.在小组间无法提供公平的竞争，从而打击部分学生学习的积极性.理想情况下，小组在各个知识点上的平均掌握程度相等时，小组之间的知识水平最为均衡.

令st表示所有学生（学生数量N）在知识点t上掌握程度的均值.

令sj，t表示小组j中各学生在知识点t上掌握程度的均值.

其中：zj表示小组gj中的学生数量.显然当所有小组在知识点t上掌握程度的均值sj，t等于知识点k的整体掌握矩阵st时，所有小组在知识点t上的知识水平最为均衡.因此对于所有小组（分组数量M）在知识点t上的均衡率可以表示为：

v(t)的值越接近1，所有小组在知识点t上的知识水平越均衡.同理扩展到其他知识点，则分组方案的整体知识均衡率可以表示为：

在进行分组时，既要考虑分组方案的整体知识互补率U，又要考虑分组方案的整体知识均衡率V，因此分组的目标函数可以定义为：

其中：w1为知识互补率的权重系数，w2为知识均衡度的权重系数.w1和w2的值可以依据场景需要进行设置.在分组时，需要最大化F的值来提高分组方案的整体知识互补度和整体知识均衡度.

2.2 分组方法

首先使用K−means 聚类算法，将认知状态相似的学生分到同一簇中，然后将簇中的学生逐个分到各个小组中，从而达到组内成员知识互补的效果.但经典K−means 算法在进行聚类时，无法保证聚类后，每个聚簇中的样本数量均衡，若簇中的学生数量大于小组数量，依据鸽巢原理可知，必然会造成同一个簇中的多个学生分到同一小组的情况，降低了小组成员的知识互补度.因此本文基于均衡聚类算法对学生进行聚类，该算法可以限定聚簇中样本的数量，从而达到聚簇规模相近的目的.

使用K−means 算法进行聚类时，K值的选择尤为重要.因为聚类后，要将聚簇中的学生逐一分配到各个分组中，为保证簇的大小尽量均衡，各个簇内的学生数量，应接近分组数量M.若各个簇内的学生数量相近（数量差值不超过1），则聚簇的数量K可以通过如下方式进行计算，

即聚簇数量K等于学生数量N除以分组数量M的整数部分.此时再进行均衡聚类时，便可以确保簇内的学生数量接近于分组数量M，且聚簇规模相近.

完成学生聚类后，下一步，需要将簇中的学生逐一分配到各个分组中.聚簇后，簇内的学生具有相似的认知状态，簇间的学生认知状态存在较大差异，可以达到知识互补的效果.

传统分配方案是将簇中的学生随机分配到各个聚簇中，这种分配方案虽然能在一定程度上达到组内知识互补、组间知识均衡的效果.但是分配结果不够稳定，可能会造成组内成员互补性较差（将不同簇中认知状态最相似的学生分到同一组中）或组间均衡度较差（将认知状态较好或较差的学生分配到同一组中）的现象.

为了解决这一问题，在组员分配时，定义的组内知识互补率和组间知识均衡率作为分组依据，分组时需确保目标函数最大化.具体分组过程如算法1 所示.

算法第1 步是初始化学生分组groups，记录每个学生所属的分组编号，长度为N.算法的第2 步用于记录将聚簇中学生分配到各个分组后剩余的学生（聚簇中的学生数量可能大于分组数量）.

算法的第3 步到第10 步，依据目标函数，遍历每个聚簇，将聚簇中的样本分配到各个分组中，并记录下尚未分组的学生.

算法的第11 步到第14 步是将未分配的学生分配到各个分组中.分组时除了要确保目标函数最大外，还需保证分组中的学生人数不能超过设定的最大值.

3 实验分析

3.1 实验数据

实验从学生规模、小组规模和知识规模三个维度，构建了9 个仿真数据集，验证算法在不同维度下的分组效果.其中学生规模表示参与分组的学生总数，小组规模表示小组内成员的数量，知识规模表示认知状态中包含的知识点数量.仿真数据集的相关配置如表2 所示.其中前3 个数据集用于考查学生规模对分组效果的影响，中间3 个用于考查小组规模对分组效果的影响，最后3 个用于考查知识规模对分组效果的影响.

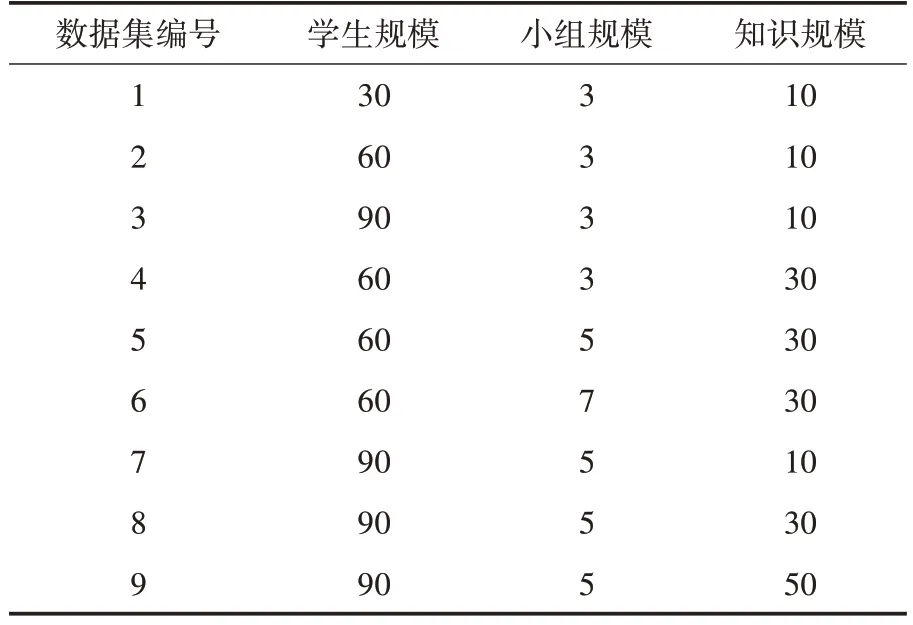
表2 数据集配置

3.2 对比算法

在实验中对比了本文提出的互补均衡分组方法（CBKM）、随机分组方法（RAND）、K−means 两阶段分组方法（KM）和约束K−means两阶段分组方法（BKM），分析了4 种模型在组内知识互补率和组间知识均衡率两项指标上的性能表现.

为了确保实验结果稳定可靠，实验中，每个算法在每个数据集上均进行了10 次随机实验，并用10 次随机实验的均值作为最终的实验结果.

3.3 结果分析

实验从3 个维度对分组效果进行分析.

学生规模维度.图2 从学生规模维度给出了不同算法生成分组方案在组内知识互补率和组间知识均衡率两项指标上的对比结果.图2 显示本文提出的知识互补均衡分组方法（CBKM），明显优于现有的分组方法，可以达到更高的组内知识互补和组间知识均衡的效果，有助于提升组内学生相互学习、互相帮助，组间相互竞争、共同提高的协作学习效果.

图2 不同学生规模下互补率与均衡率对比

小组规模维度.对于小组规模维度，对比了小组成员为3 人、5 人、7 人情况下，不同算法生成的分组方案效果，如图3 所示.无论在组内知识互补率和组间知识均衡率上，本文提出的知识互补均衡分组方法（CBKM）均取得了最佳效果.需要指出的是，从图3 可以看出，随着小组人数的增加，组内两两成员的平均知识互补率均值呈现下降趋势，这是因为随着小组成员的增加，在知识点总量不变的情况下，两两成员的知识差异性均值在减小，造成了平均互补率的下降.因此在实际分组过程中，并不是成员数越多，越有助于组内成员沟通和协作.

图3 不同小组规模下互补率与均衡率对比

知识规模维度.知识规模维度越大，考虑的特征数量越多，人工分组的难度越大.因此在多特征场景下，常使用基于规则的自动化分组方法.实验分别仿真模拟了10 个知识点、30 个知识点、50 个知识点三种知识规模，并考察了不同算法的分组效果.从图4 中可以看出，无论知识规模是10 个、20 个还是30 个，本文提出的知识互补均衡分组方法均优于其他方法，取得了最佳的平均互补率和知识均衡率.需要注意的是，随着知识规模的增大，组内两两成员的平均知识互补率和组间知识均衡率呈现下降趋势，这是因为随着知识总量的增加，虽然互补的知识数量在增加，但是互补的知识点数占总知识点数的比例在减少，造成组内两两成员的平均互补率随着知识规模的增加呈现下降趋势，同理，小组各个知识点掌握的均值与总体均值的偏差也会增大，组间知识均衡率随着知识规模的增加呈现下降趋势.

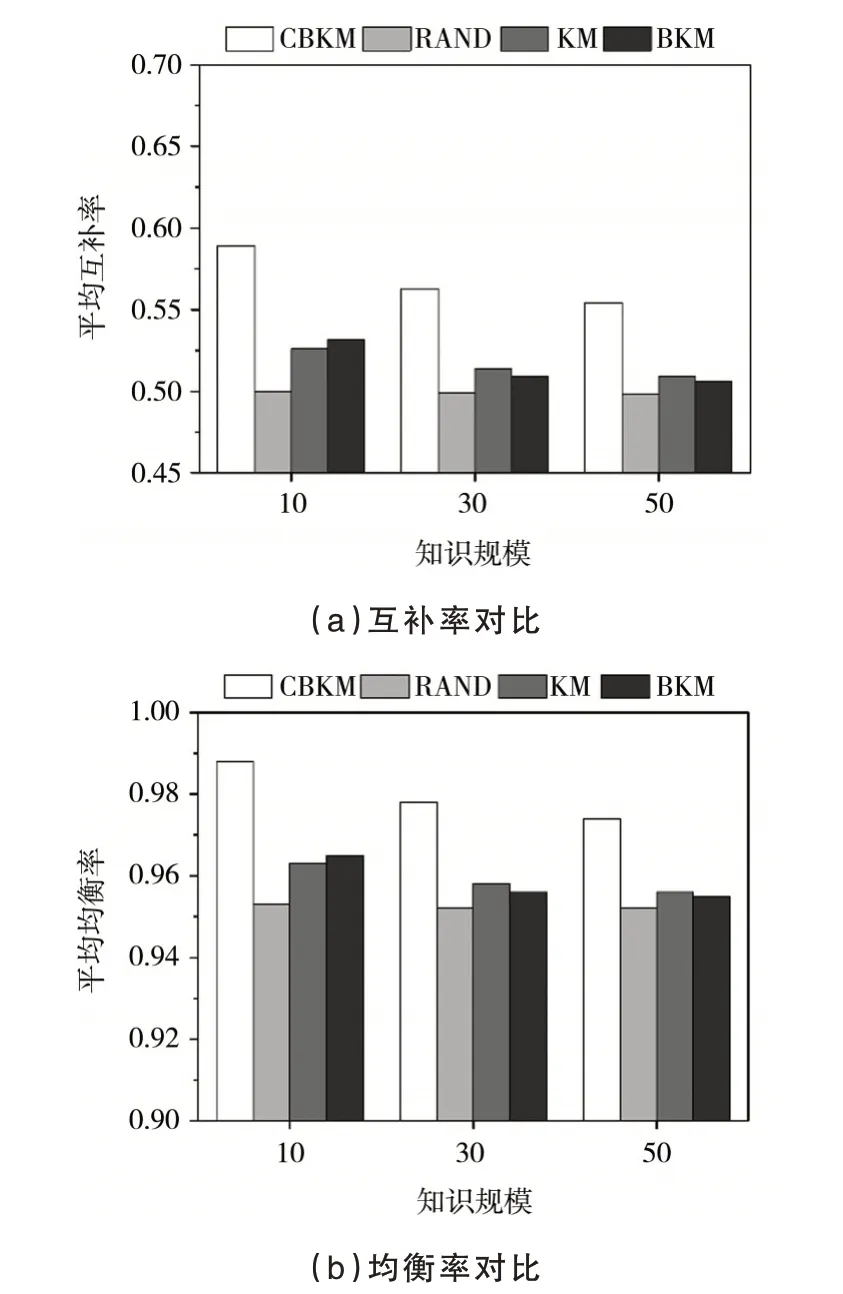
图4 不同知识规模下互补率与均衡率对比

4 结语

学生分组是协作学习的核心问题之一，学生分组主要面对两方面挑战.其一是学生特征难以获得，标注的方式繁琐且难以标准化；其二是分组后小组人数和学习能力不易均衡.本文的主要贡献是提出了一种基于认知状态的互补均衡分组模型，使用认知诊断的相关技术获取学生的认知特征，定义了学生分组的目标函数，并提出了一种组内互补、组间均衡的分组方法.在实验中对该模型和现有的三种分组方法进行对比，设置了多种数据集的配置，分别在不同的学生规模、不同的小组规模和不同的知识点规模下，验证了该模型的有效性.