手机成瘾动力学模型的定性分析

高德宝，张 桢，邱嘉仁

长时间低头玩手机的群体称之为“低头族”［1］“.低头族”亦称为手机成瘾（或手机控）群体，该群体无论何时何地都低头看屏幕，想通过盯住屏幕的方式，把零碎的时间填满.长时间低头玩手机主要有两方面隐患：一是安全隐患，低头玩手机就会忽视周围的环境情况，容易导致危险的发生.二是健康隐患，长期低头看手机，容易导致颈椎关节发生错位和视力快速下降.手机成瘾与酗酒［2−3］和吸烟成瘾［4−5］有相似之处，而且比酗酒和吸烟成瘾更具有普遍性.

手机成瘾问题日益严重，引起了人们的广泛关注.手机成瘾不仅能够导致一些疾病的发生，还会增加许多安全隐患.一些学者从生物数学［6−7］角度，应用微分动力学［8−10］研 究酗酒模型［11−12］和吸烟模型［13−14］的构建和稳定性.本文也考虑应用微分动力学的知识对手机成瘾群体进行模型构建和定性分析.

1 手机成瘾模型的构建与分析

1.1 手机成瘾模型的构建

考虑到手机成瘾群体中有主动或被动戒除手机瘾的用户，可将手机用户分为四个群体.用P(t)，C(t)，G(t)，S(t) 分别表示t时刻的潜在手机成瘾群体人数、手机成瘾群体人数、戒瘾群体人数和正常手机用户群体人数.若令N(t)表示t时刻手机用户的总人数，则

为书写方便，记P=P（t），C=C（t），G=G(t)，S=S(t).

根据四个群体之间的人员转移规律绘制的关系图如图1 所示.

图1 手机用户不同群体之间的人员转移关系图

其中：γ为手机用户的常数增加率，将新加入的手机用户看作潜在的手机成瘾用户.由于手机成瘾用户对潜在的手机成瘾用户具有一定的“传染性”，所以α1表示手机成瘾群体对潜在手机成瘾群体的有效传染率，α2表示手机成瘾群体中主动或被动向戒瘾群体的转移率，α3表示戒瘾群体向正常手机用户群体的转移率，β1表示潜在手机成瘾群体向正常手机用户群体的转移率.在戒瘾群体中，由于一部分人的自控能力不强，会重新转移到手机成瘾群体或潜在手机成瘾群体中，β2、β3分别表示戒瘾群体向手机成瘾群体和潜在手机成瘾群体的转移率，μ表示各个群体的自然退出率.图1 中的所有系数均为正数.

根据各变量之间的对应关系，图1 所对应的微分方程系统为：

基于系统（1）的实际意义，本文将在其最大正向不变集，即

内进行研究.

1.2 平衡点的存在性

系统（1）的平衡点满足如下的代数方程组.

易知，系统（1）始终存在无手机成瘾的非负平衡点

根据文献［15］中的算法，系统（1）的基本再生数为：

在式（2）中，由第3 个方程可得

将式（3）代入式（2）的第2 个方程可得

将式（3）和式（4）代入式（2）的第1 个方程可得

定理1 系统（1）始终存在无手机成瘾的非负平衡点E0(P0，C0，G0，S0).当R0>1 时，系统（1）存在唯一的正平衡点E*(P*，C*，G*，S*).

注：非负平衡点E0是所有手机用户中不存在手机成瘾用户的临界状态.当R0>1 时，手机成瘾用户会增加，正平衡点E*表示手机成瘾用户增加的上限状态.

1.3 平衡点的稳定性

定理2 当R0<1 时，系统（1）的无手机成瘾非负平衡点E0(P0，C0，G0，S0)是局部渐近稳定的.当R0≥1 时，E0是不稳定的.

证明 系统（1）在E0点的Jacobi 矩阵为：

则特征方程|J(P0，C0，G0，S0)−λE|=0 的具体表达式为：

所以特征方程的前两个根为：

若令λ3，λ4为特征方程的后两个根，有

当R0<1 时，K<0，所以λ3⋅λ4>0.因此λ3，λ4为一对共轭复根或一对同号非零实根.

当K<0 时，有

所以λ3+λ4<0，从而λ3和λ4的实部为负数.

综上所述，当R0<1 时，λi(i=1，2，3，4)的实部均为负数.因此，系统（1）的无手机成瘾非负平衡点E0是局部渐近稳定的.

当R0≥1 时，K≥1，从而λ3⋅λ4≤0.因此λ3和λ4中有一个非负实根.所以，当R0≥1时，系统（1）的无手机成瘾非负平衡点E0是不稳定的.

定理3 当R0>1 时，系统（1）的唯一正平衡点E*(P*，C*，G*，S*)是局部渐近稳定的.

证明 系统（1）在E*点的Jacobi 矩阵为：

则特征方程|J(P*，C*，G*，S*)−λE|=0 的具体表达式为：

因此λ1=−μ<0，而其余的三个特征值满足如下方程：

根据Hurwitz 准则［15］可知，方程（6）的所有根具有负实部.

综上所述，方程（5）的所有根具有负实部.因此，当R0>1 时，系统（1）在唯一的正平衡点E*(P*，C*，G*，S*)处是局部渐近稳定的.

定理4 当R0<1 时，系统（1）的无手机成瘾非负平衡点E0(P0，C0，G0，S0)是全局渐近稳定的.

证明 考虑系统（1）的第1 个方程和第2个方程构成的子系统：

所以该系统在其可行域中无闭轨，结合无手机成瘾非负平衡点的局部渐近稳定性，由Bendixon−Dulac 判别法可知，系统（1）的无手机成瘾非负平衡点E0(P0，C0，G0，S0)在D上是全局渐近稳定的.

同理可知下面的定理5 成立.

定理5 当R0>1 时，系统（1）的唯一正平衡点E*(P*，C*，G*，S*)是全局渐近稳定的.

根据定理4 可知，当R0<1 时，手机成瘾用户会逐渐减少，直至达到灭绝点E0.根据定理5 可知，当R0>1 时，手机成瘾用户会逐渐增加，直至达到平衡点E*.

2 数值算例

为了验证系统（1）的理论结果，给出此系统的数值模拟.

取γ=0.06，μ=0.07，α1=0.15，α2=0.03，α3=0.04，β1=0.1，β2=0.05，β3=0.06，则系统（1）的非负平衡点与基本再生数分别为E0=(0.353，0，0，0.504)，R0=0.568.

再取初值P(0)=5，C(0)=30，G(0)=40，S(0)=60，利用Matlab 软件对系统（1）进行数值模拟，所得结果如图2 所示.

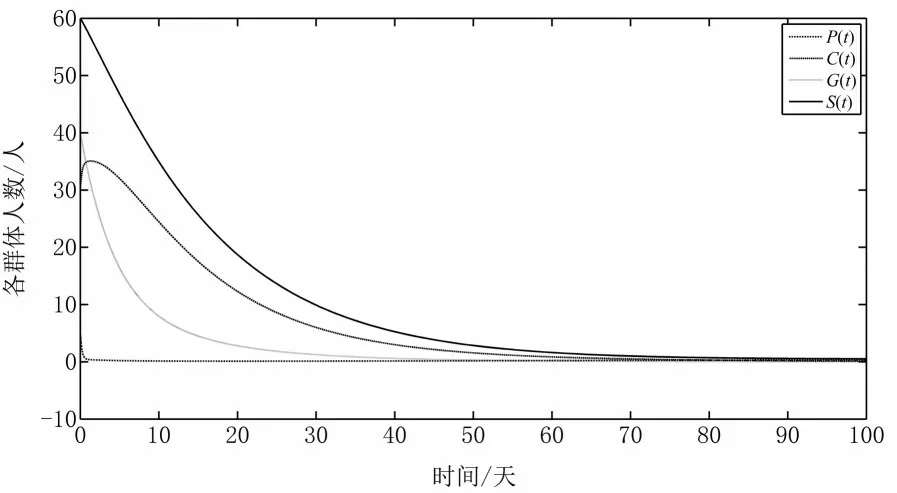
图2 系统（1）非负平衡点的全局稳定性

从图2 可以看出，当R0<1 时，随着时间的流逝，手机成瘾群体会消失.

取γ=0.7，μ=0.08，α1=0.15，α2=0.03，α3=0.06，β1=0.25，β2=0.36，β3=0.07，则系统（1）的唯一正平衡点与基本再生数分别为E*=(0.607，5.719，0.301，2.123)，R0=3.495.

再取初值P(0)=10，C(0)=20，G(0)=40，S(0)=70，利用Matlab 软件对系统（1）进行数值模拟，所得结果如图3 所示.

图3 系统（1）唯一正平衡点的全局稳定性

从图3 可以看出，当R0>1 时，系统（1）的解最终趋向于一个正的非零常数，表明手机成瘾群体将会持续存在，且E*是全局渐近稳定的.

3 结语

本文构建了手机成瘾群体人数动态变化的动力学模型，得到其基本再生数.若基本再生数大于1，则手机成瘾群体人数会动态变化并趋向于一个常数.若基本再生数小于1，则手机成瘾群体会逐渐消失，这两个结论在数值算例部分得到了验证.