基于CART 和聚类分析的古代玻璃分类预测模型研究

邵光明，夏贤齐，殷何杰

随着考古工作的不断深入，我国已出土了数以千计的古代玻璃制品，并且这些玻璃制品主要出土于古代丝绸之路沿线，这从侧面反映了丝绸之路是我国古代重要的贸易之路，也是重要的中西文明交流之路［1］.我国最早的玻璃类型主要有铅钡硅酸盐玻璃和钾硅酸盐玻璃等，但是由于年代久远，玻璃埋在土中（如古墓内的葬品）会受到环境影响而风化［2］，玻璃风化后往往风化产物会堆积在玻璃表面形成白色斑点或大片的雾状物从而影响其化学成分比例，进而影响对其类别的鉴别，这对我国玻璃制品化学成分的研究及玻璃文物类别鉴定造成了较大困难.

目前，关于古代玻璃制品的研究部分集中在其出土地或者其制造技术的起源［3］，部分集中在文物的历史发展或者是古代玻璃制品的特点［4］，还有部分集中在分析其成分特点或制造工艺［5］，鲜有文章关注其化学成分鉴别和分析.由于风化程度的不同，不同古代玻璃制品鉴别的困难程度也有所不同.玻璃制品的研究还可使用回归分析、主成分分析［6］、机器学习［7］、X 射线［8］等方法，这些方法可以鉴别玻璃制品的成分，但是大部分文献没有涉及对未知化学成分的预测分析.本文构建了CART 和聚类分析预测模型，使用聚类分析模型对不同化学成分进行比例分析，进而通过不断迭代得出最优的聚类中心点，即选取合适的化学成分，利用CART 模型，将未知玻璃制品的化学成分放入模型中训练，最后对其类别进行正确的分类.

1 模型构建

1.1 聚类分析

①系统聚类.系统聚类是将每个样本独立化，按照距离，将最近的两个样本合为新类，计算新类与其他类的距离，重复此过程，直到所有样本都在一个大类中.最后绘制聚类图，确定类的个数.

②K−means 聚类.K−means 的核心思想是首先从数据集中随机选取k个初始聚类中心Ci(1 ≤i≤k)，计算其余数据对象与聚类中心Ci的欧氏距离，找出离目标数据对象最近的聚类中心Ci，并将数据对象分配到聚类中心Ci所对应的簇中，然后计算每个簇中数据对象的平均值作为新的聚类中心，进行下一次迭代，直到聚类中心不再变化，迭代停止［9］.

1.2 主成分分析

主成分分析法是Pearson 于1901 年首次提出的，通过研究指标体系的内在结构关系，把多指标转化成少数几个互相独立而且包含原有指标大部分信息的综合指标的多元统计方法，其优点是此方法确定的权数是基于数据分析而得到的指标之间的内在结构关系，而且得到的综合指标（主成分）之间彼此独立，这使得分析评价结果具有客观性和可确定性［10］.其步骤如下：

①按列计算均值和标准差，得出标准化矩阵.

②计算协方差矩阵R的特征向量和特征值λ1≥λ2≥…≥λp≥0（R是半正定矩阵）.

③通过式（1）和式（2）分别计算贡献率和累计贡献率，其中累计贡献率越大，说明其成分包含的信息量越多.

1.3 决策树模型

决策树［11］本质上是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别［12］.使用决策树前，先进行选择，判断哪一个特征确定了树的功能，并进行子表划分.CART 算法常采用基尼系数来划分特征.基尼系数即一个样本被分错的概率.在样本数量为d的样本集D，k为种类个数，每个种类对应的样本数量为Ck时，计算公式如下：

式中：p(Xi)表示样本种类为i时被选中的概率，计算公式为

2 结果与讨论

2.1 数据处理

数据来源于2022 年全国大学生数学建模竞赛官网提供的古代玻璃制品的相关数据.现已知这些文物样品的化学成分比例和玻璃类型为高钾玻璃和铅钡玻璃.由于检测手段等原因可能导致成分比例的累加为非100%的情况，因此，规定在85%～105%之间才视为有效数据.将数据进行求和会发现15 号和17号的累加不在范围之内需剔除.数据存在空白值，不属于缺失值，将其设为0，以此方便后面模型的计算.对数据进行标准化，本文采用Z 标准化方法.

2.2 结果分析

①聚类分析结果.针对玻璃种类是否风化进行分析，将系统聚类的结果与实际值进行比较，从而判断分类标准划分的合理性，将检测到的主要成分指标通过SPSS 25.0 软件进行系统聚类，聚类结果谱系图如图1 所示.

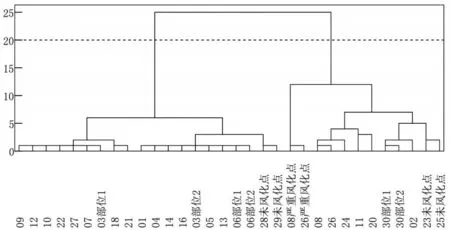
图1 玻璃类型高钾与铅钡系统聚类结果谱系

从图1 可以看出，当距离大于20 时，其呈现明显的两大趋势.聚类结果的两个大类可以反映不同风化程度的玻璃样本.即距离小于20 的样本在某种程度上具有相似的风化特征，而距离大于20 的样本则表现出更大的差异性.

K−means 聚类之后对分类数目进行敏感性检验得到的结果如表1 所示.

表1 敏感性检验结果

从表1 可以看出，分类数目与准确率不成正比，当分类数目为3 时，准确率最高为89.71%.然而，在其他分类数目下，准确率存在波动性且有下降趋势，表明过多或过少的分类数目可能导致分类结果的不准确.由此可以看出，从获得的数据中将古代玻璃类别分为高钾类和铅钡类两大类和三个亚类是最佳选择.

此分类方案可为文物研究和管理提供重要的分类依据，有助于深入理解文物的特征和更为精确的分类关系.为确保该分类方案的有效性和可靠性，仍需要进一步研究与验证.

②主成分分析结果.由于本文指标较多可能导致高维度数据，且部分指标存在大量的零值.为降低维度减少数据的复杂性和数据的稀疏性，本文利用主成分分析法，将所收集到的玻璃文物数量作为样本，14 个化学成分作为指标，建立矩阵，运用SPSS 25.0 软件计算相关矩阵和特征值等.主成分分析的特征根如图2 所示.

图2 主成分分析的特征根

从图2 可以看出不同特征根的特征值大小.当提取的因子小于6 个时，特征值变化较大，这表明新增的因子对解释原有变量的贡献较大.当提取的因子大于6 个时，特征值变化较小，增加特征值对原有变量贡献相对较小，由此可知，提取前六个因子对原有变量有显著作用.

③CART 决策树预测.根据化学成分的比例大小，对被分为高钾和铅钡的两类玻璃文物，通过使用Python 进行训练，得到一个决策树模型，如图3 所示.

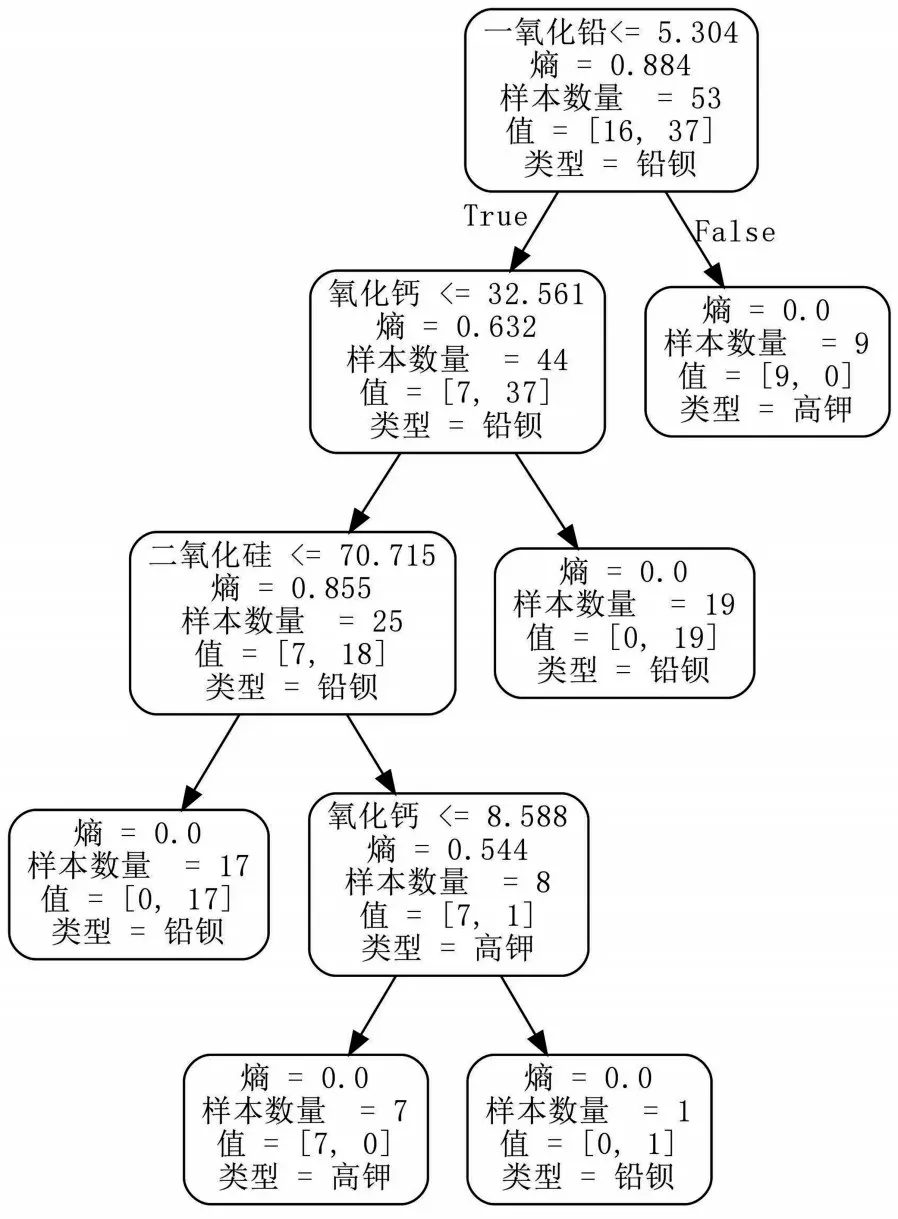
图3 决策树模型结构

从图3 可以看出，沿着决策树不同的分支路径进入可以帮助其对玻璃文物进行分类和识别.这种基于决策树模型的分类和识别方法可以为玻璃文物研究和鉴定提供有力的支持.

将未知文物的化学成分数据作为测试集，并通过已建立的CART 决策树模型进行预测.模型根据输入A1～A8 的特征值，对每个未知文物进行玻璃类型的预测，预测结果如表2所示.

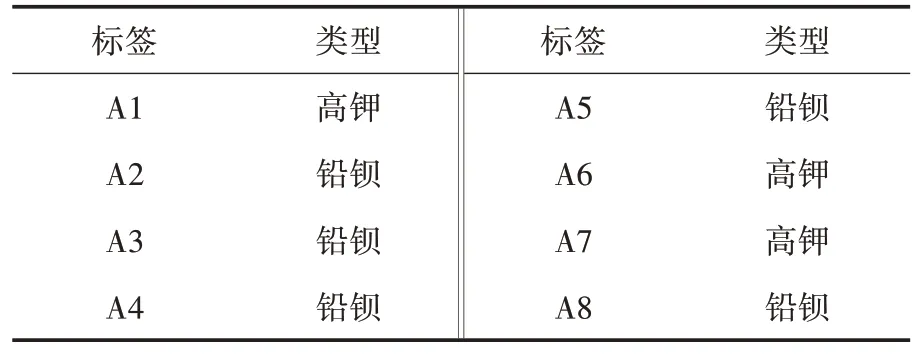
表2 未知文物预测结果

从表2 可以看出，基于决策树模型根据训练数据中的特征值和对应的已知玻璃类型进行学习，得出的预测结果为高钾类或铅钡类.例如，A1、A6 和A7 被预测为高钾类，而A2、A3、A4、A5 和A8 被预测为铅钡类.

3 结语

文章使用Python 和SPSS 软件，构建CRAT决策树分类预测模型，对古代玻璃制品进行分类预测，采用系统聚类和K−means 聚类方法对古代玻璃制品进行分类，从而提高了模型的合理性和准确性.

本研究存在的局限性：一是模型预测结果需要进一步验证，以确保结果的精确性与模型的稳定性；二是由于不同时期和地区的古代玻璃制品存在差异性，可能需要更多的样本数据和特征信息，以改进分类预测的效果.后续将针对这些局限性进行认证.