Recursive filtering of multi-rate cyber-physical systems with unknown inputs under adaptive event-triggered mechanisms∗#
2024-03-01YingSUNMiaomiaoFUJingyangMAOGuoliangWEI
Ying SUN ,Miaomiao FU ,Jingyang MAO ,Guoliang WEI
1Business School, University of Shanghai for Science and Technology, Shanghai 200093, China
2Shanghai Caoyang Vocational School, Shanghai 200333, China
3School of Electrical and Electronic Engineering, Shanghai Institute of Technology, Shanghai 201418, China
4School of Intelligent Emergency Management, University of Shanghai for Science and Technology,Shanghai 200093, China
Abstract: Cyber-physical systems(CPSs)take on the characteristics of both multiple rates of information collection and processing and the dependency on information exchanges.The purpose of this paper is to develop a joint recursive filtering scheme that estimates both unknown inputs and system states for multi-rate CPSs with unknown inputs.In cyberspace,the information transmission between the local joint filter and the sensors is governed by an adaptive event-triggered strategy.Furthermore,the desired parameters of joint filters are determined by a set of algebraic matrix equations in a recursive way,and a sufficient condition verifying the boundedness of filtering error covariance is found by resorting to some algebraic operation.A state fusion estimation scheme that uses local state estimation is proposed based on the covariance intersection (CI) based fusion conception.Lastly,an illustrative example demonstrates the effectiveness of the proposed adaptive event-triggered recursive filtering algorithm.
Key words: Cyber-physical systems;Multi-rate;Joint recursive filtering;Adaptive event-triggered mechanisms;Unknown inputs
1 Introduction
Recursive filters,widely used in various practical engineering,computer science,instrumentation,and other fields,have sparked significant research interest (Glentis,2008;Gravina et al.,2017;Sheng et al.,2018;Kumar et al.,2019;Chen WB et al.,2022;Xie XP et al.,2022;You et al.,2022).When focusing on cyber-physical systems (CPSs) with the integration of cyberspace and physical space,the traditional single-sensor monitoring and tracking function is no longer sufficient,necessitating the research of multi-sensor systems (Su et al.,2022).Multisensor synthesis algorithms can be categorized into two canonical forms: centralized algorithms and distributed algorithms (Ju et al.,2022;Ge et al.,2023;Ning et al.,2023).In a centralized manner,a local filter can be first designed to obtain the estimation of the system state,and then the estimated states are sent to the fusion center to improve the estimation precision and robustness via information fusion.
Due to the increasing complexity,CPSs appear to have some prominent characteristics,such as multiple rates of information collection and processing,unknown inputs (control demands or decisions),as well as dependency on information exchanges(Chen W et al.,2019;Shakiba et al.,2022;Song HF et al.,2022).The treatment of unknown inputs in early studies can be categorized into either of the following two approaches: such inputs could be(1)directly ignored,which inevitably leads to modeling bias,or(2) described by additional models such as random processes(Xing et al.,2021)or constant bias(Friedland,1969),which depends on some prior information.For instance,the unbiased minimum variance state estimation was initially proposed in Kitanidis(1987)for the case with unknown inputs or parameters.However,the filter does not achieve global optimality in the mean square sense.Then,Darouach and Zasadzinski (1997) proposed an unbiased minimum variance filter with unknown exogenous inputs,and proved that it is optimal in the sense of an unbiased minimal variance.The estimator design can vary greatly as to whether the measurement equation contains unknown inputs.Furthermore,for systems that do not assume any specific structure for the direct feed-through matrix,the singular value decomposition method can be employed to separate the measurement equation into two parts: one part does not involve the direct feedforward matrix,while the other part includes such a matrix with full rank(see Yong et al.(2016)for some latest literature).
Due to different physical limitations and calculation capabilities in cyberspace,different components such as sensors,filters,and state evolution in CPSs may have different signal frequencies.Hence,it is unreasonable to use only traditional single-rate sampling methods.Nowadays,the issue of multi-rate sampling has received attention,with some interesting results being reported in the literature(Tan et al.,2017;Liu S et al.,2018;Zhao and Liu,2022).Generally speaking,the lifting technique can be used to overcome the challenges from multiple rates.On the other hand,the time-triggered scheme of transmitting data in a fixed period has been widely used in control engineering (Gungor et al.,2010).However,the sampling data based on the time-triggered mechanism must carry data with minimal fluctuations.The frequent transmission will lead to the waste of communication resources and result in a tremendous increase in computing costs.Event-triggered communication protocols transmit signals only when specific prior conditions are met,thereby reducing the loss of network communication resources(Sun et al.,2021;Ge et al.,2022;Han et al.,2022b;Liu ZQ et al.,2022;Xie ML et al.,2022;Zhang XM et al.,2023).In the realm of connected autonomous vehicles on highways,a method for event-triggered robust control has been developed.This method aims to minimize the usage of communication resources while ensuring the stability of virtual platoon systems,even in the presence of time-varying uncertainties (Han et al.,2022a;Hu et al.,2022).Consequently,the influence of events’occurrence on the event-triggered scheme has sparked the research curiosity of researchers.This approach has found applications in diverse system categories,including but not limited to sensor networks,complex networks,and multi-agent systems (Wang et al.,2016;Song WH et al.,2019;Xing et al.,2021;Yang et al.,2022).
Note that the above mentioned event-triggered mechanisms are all based on a static rule that data will be released only when the measurement difference meets a predetermined fixed threshold.In practical research,it is difficult to directly give a reasonable fixed threshold,let alone in multi-rate systems with unknown inputs.To address such issues,an adaptive event-triggered mechanism with adaptive threshold parameters was developed(Zhang H et al.,2019;An et al.,2022),and this mechanism provides more flexibility in scheduling data transmission.In recent times,a mechanism for triggering adaptive events has been suggested which incorporates an extra function of internal dynamic variables to guarantee the stability of the resultant closed-loop system(Girard,2015).In addition,an event-triggered protocol has been developed to reduce the number of instances of communication between adjacent sensors,where the triggering threshold of the event-triggered protocol is a time-varying threshold parameter that can reach the upper and lower bounds (Ge et al.,2019).Therefore,optimizing event-triggered parameters is meaningful,which also constitutes one of the motivations of this paper.
In response to the above analysis,the main challenge we face is the quest for a means to construct a fusion recursive filter with an adaptive eventtriggered mechanism.We also need to verify the sufficient conditions for the boundedness of the filter error covariance and ensure filtering performance under information fusion.According to the previous discussions,this paper focuses on the issue of adaptive event-triggered recursive filtering for multi-rate CPSs with unknown inputs.The main contributions can be summarized as follows:
1.A joint recursive filter with an adaptive eventtriggered mechanism is constructed to simultaneously estimate unknown inputs and system states.
2.The ideal filter gains are obtained by recursively solving two algebraic matrix equations using the lifting technique.
3.A sufficient condition is derived using classical algebraic operations to verify the boundedness of the filtering error covariance.
4.The filtering performance is enhanced by employing a famous state fusion scheme in the covariance intersection(CI)based fusion conception.
2 Problem formulation
Consider the following class of CPSs with unknown inputs:
wherex()∈Rnxrepresents the system state,d()∈Rndrepresents unknown inputs,ω() is a zero-mean Gaussian white noise sequence with covarianceW()>0,andA() andB() are known time-varying matrices with appropriate dimensions.Here,we assume thatis the state updating period of the system,wherehis a known positive constant.
According to the above CPSs with unknown inputs,interested information is sampled by multiple sensors with distinct rates:
whereyi(lt)∈Rnyis theithsensor measurement output,νi(lt)is the zero-mean measurement noise of sensoriwith covarianceVi(lt)>0,andCi(lt) is a known time-varying matrix with appropriate dimensions.The system is measured bymsensors with a sampling periodah≜lt+1-lt,wherea ≥2 is a known positive integer.
Assumption 1All stochastic variables,i.e.,ω() (t ≥0),νi(lt) (1≤i ≤m,k ≥0),andx(r0),are uncorrelated mutually.
It becomes evident from Eqs.(1) and (2) that the system under consideration is fundamentally a multi-rate system.The lifting technique is employed to streamline the filter design process,thereby ensuring that the multi-rate CPS undergoes conversion into a single-rate system.The corresponding dynamics with the timescaleltis reorganized as follows:
where,forq=1,2,···,aandj=1,2,···,q-1,
For notational simplicity,we define
Furthermore,the compact form is received as follows:
Remark 1In real-world scenarios,dynamic models often have varying frequency attributes,and the sampling rate for different system components tends to differ.In this study,the system operation involves two rates: system state update rate and measuring sampling rate.To simplify subsequent research,we assume that these two rates are integer multiples of each other,and then use lifting technology to convert them into a unified rate for analysis.
To optimize communication efficiency,one can implement an adaptive event-triggered communication protocol between the sensor and the filter.This protocol ensures that the measured signal is transmitted only when the preset triggering conditions are met.To model such a rule,one first constructs the following function:
whereσi(lt)=yi(lt)-yi() withyi() is the last transmitted measurement andρi(lt) is the adaptive dynamic parameter.In light of the latest eventtriggered instanton the sensori,the next eventtriggered instantis determined by the following iterative relationship:
Here,the parameterρi(k) is adaptive and satisfies the time-varying law:
whereλ>0 and∈[0,1] are suitable positive scalars.The initial value ofρ(lt) is denoted asρ(0)with 0≤ρ(0)≤.
Under such a communication mechanism,forwe construct a local filter for theithnode as follows:
In what follows,substituting the first two formulas into Eq.(4)results in
Denoting the estimation error of the unknown input,the prediction error,and the filtering error as
To eliminate the influence of unknown input on the error system,the designed gain needs to satisfy the following constraint:
Noting the definition ofNi(lt+1),one can easily inter from Eq.(13)that
Finally,Eqs.(8)and(12)can be rewritten as follows:
In summary,the purpose of this paper is to develop a joint filter(4)such that
2.the filter gainsKi(lt+1) andLi(lt+1) are parameterized to minimize the above upper bounds at every time step,and
3.a state fusion scheme leveraging local state estimation is proposed via the CI-based fusion conception.
3 Main results
In this section,we initially derive the upper bound of the error covariance matricesΞi,d(lt) andΞi,x(lt+1|lt+1)for the undetermined inputs and state of the system.Subsequently,we formulate the necessary filter gains state of the system and formulate the necessary filter gainsLi(lt+1) andKi(lt+1)through minimization of the aforementioned upper limits.Following this,we identify a sufficient condition that guarantees the boundedness of the upper limit of the obtained filtering error covariance.Lastly,we establish a state fusion estimation scheme within the CI fusion framework by leveraging local state estimation techniques.
3.1 Design of local filters
At the outset,let us give the following lemmas for the subsequent theoretical derivation:
Lemma 1(Boyd et al.,1994) For an arbitrary positive scalarαand arbitrary matrices with compatible dimensionsX1,X2,andY=YT≥0,one has
Lemma 2(Tian et al.,2019) Consider the timevarying functionρi(lt) withρ(0)≤given by Eq.(7).For the predetermined constantλand any variableσi(lt),the sequence{ρi(lt)}is monotonically increasing and satisfiesρ(0)≤ρi(lt)≤.
Theorem 1Consider the jointly local filter(8)under event generator conditions(5)–(7)for multi-rate CPSs consisting of the time-varying system (1) and measurements (2).Under the uncoupling condition(13),the bounds of filtering error covariance matrices of unknown inputs and system states are
ProofThe proof of this theorem is provided in the supplementary materials.
Theorem 2Consider the jointly local filter(8)under event generator conditions(5)–(7)for multi-rate CPSs consisting of the time-varying system (1) and measurements (2).Under the uncoupling condition(13),the bounds of filtering error covariance matrices of unknown inputs and system states are minimized by selecting the following two gains:
ProofThe proof of this theorem is provided in the supplementary materials.
3.2 Boundedness analysis
In this subsection we discuss the boundedness of filtering error dynamics.For the sake of subsequent discussion,we first introduce the following definitions and assumptions:
Definition 1For real numbersc1>0,c2>0,and 0 holds∀l>0,then the stochastic process(lt|lt) is exponentially bounded in the mean square sense. Assumption 2Given positive real constants,,the following conditions hold for the addressed multi-rate CPSs consisting of the time-varying system(1)and measurements(2). Theorem 3Under Assumption 2,consider the jointly local filter (8) under event generator conditions (5)–(7) for multi-rate CPSs consisting of the time-varying system(1)and measurements(2).Under the uncoupling condition (13),if the joint filter(8) adopts the gains designed in Theorem 3,if the following condition is true,where then the filtering error dynamics (16) is exponentially bounded in the mean square sense. ProofThe proof of this theorem is provided in the supplementary materials. For the multi-sensor system considered in this paper,a CI fusion estimation scheme is adopted,considering the objectives of avoiding the calculation of cross-covariance and ensuring the robustness of state estimation. The state fusion estimate and state fusion covariance are represented by(lt|lt) andΞf,x(lt|lt),respectively.The fusion scheme is as follows: To improve the robust accuracy of CI-based fusion,parameterwisatisfies the following nonlinear constrained optimization problem: Theorem 4Consider the jointly local filter(8)under event generator conditions(5)–(7)for multi-rate CPSs consisting of the time-varying system (1) and measurements (2).The CI-based fusion estimation schemes(24)and(25)are consistent: ProofConsideringPi,x(lt+1|lt+1)≤Ξi,x(lt+1|lt+1),the proof of Theorem 4 can be obtained directly from the relevant proof presented in Deng et al.(2013). Remark 2The problem of recursive filtering for a class of multi-rate CPSs under the event-triggered protocol has been successfully solved.In Theorem 1,we derive an upper bound on the filtering error covariance.We then determine the filter gain to minimize this upper bound and obtain the smallest possible upper bound in Theorem 2.These derived minimum upper bounds provide comprehensive information about the multi-rate sampling and event-triggered mechanisms.Furthermore,Theorem 3 presents sufficient conditions to guarantee the exponential boundedness of the filtering error in terms of dynamic mean square. In this section,we demonstrate the effectiveness of the filter design approach explained in the present study by providing a numerical illustration. The parameters of the considered CPS(1)monitored by sensors(Eq.(2))are set as follows: Covariance matrices of process noiseω(rl)and measurement noiseνi(lt)are set as 0.001,and the initial value of the system statex0is uniformly distributed over [0.18,0.16].For the dynamic triggering conditions (6) and (7),the thresholds are chosen asρ0=0.01,=0.05,andλ0=0.01.Based on these parameters,the filter parametersKiandLifori=1,2 can be calculated at each iteration according to Eqs.(19)and (20). The simulation results are presented in Figs.1–7.Specifically,Figs.1 and 2 display the trajectories of the true states and the corresponding estimates,showing that the estimation trajectories accurately track the true ones.Figs.3–6 depict the trace of the minimum upper bound and the mean square error (MSE) for the state estimation.The triggering instants of each sensor node under the dynamic event-triggered mechanism can be observed in Fig.7.Overall,the simulation results demonstrate the feasibility of the dynamic event-triggered filtering algorithm proposed in this paper. Fig.1 State estimates of x1 and x2 and their fusion estimates (References to color refer to the online version of this figure) Fig.2 Unknown inputs and their estimates(References to color refer to the online version of this figure) Fig.3 Upper bound of the trace of filtering error covariance of system state x1 Fig.4 Upper bound of the trace of filtering error covariance of system state x2 Fig.5 Upper bound of input Fig.6 Upper bound of the trace of filtering error covariance of unknown inputs Fig.7 Triggering instants Remark 3To conserve sensor energy,we use a pre-determined event-triggered mechanism to regulate data transmission between the sensor and the estimator.Furthermore,we present an illustrative example to demonstrate the effectiveness and applicability of the proposed filter design technology.The triggering moment determined by the eventtriggered protocol clearly shows a significant reduction in the number of data transmissions. In this paper,we use an event-based adaptive mechanism to study the filtering problem for CPSs with unknown inputs.To reduce communication costs,we use a dynamic-event-based strategy to determine when a sensor node sends its measurements to neighbors.The system operation consists of two rates,namely the system state update rate(i.e.,the measured sampling rate)and the measuring transmission rate (i.e.,the estimated output rate).Our goal is to set enough conditions to guarantee an upper bound on the filter error covariance.We use a specific set of recursions to obtain the parameters of the desired filter.On this basis,a state fusion estimation scheme based on the CI-fusion method is proposed using local state estimation.Finally,we verify the effectiveness of the proposed adaptive event-triggered recursive filtering algorithm through an example.Further research topics include extending this algorithm to other control or filtering mechanisms with time-varying topologies.Additionally,the exploration of alternative communication protocols such as the Round-Robin protocol,the weighted Try-Once-Discard protocol,and the random communication protocol is being investigated,with these being anticipated to serve as possible replacements for dynamic event-triggered mechanisms. Contributors Ying SUN and Miaomiao FU designed the research and processed the data.Ying SUN drafted the paper.Jingyang MAO helped organize the paper.Ying SUN,Miaomiao FU,and Guoliang WEI revised and finalized the paper. Compliance with ethics guidelines Ying SUN,Miaomiao FU,Jingyang MAO,and Guoliang WEI declare that they have no conflict of interest. Data availability The data that support the findings of this study are available from the corresponding author upon reasonable request. List of supplementary materials 1 Proof of Theorem 1 2 Proof of Theorem 2 3 Proof of Theorem 33.3 Fusion estimation scheme
4 An illustrative example

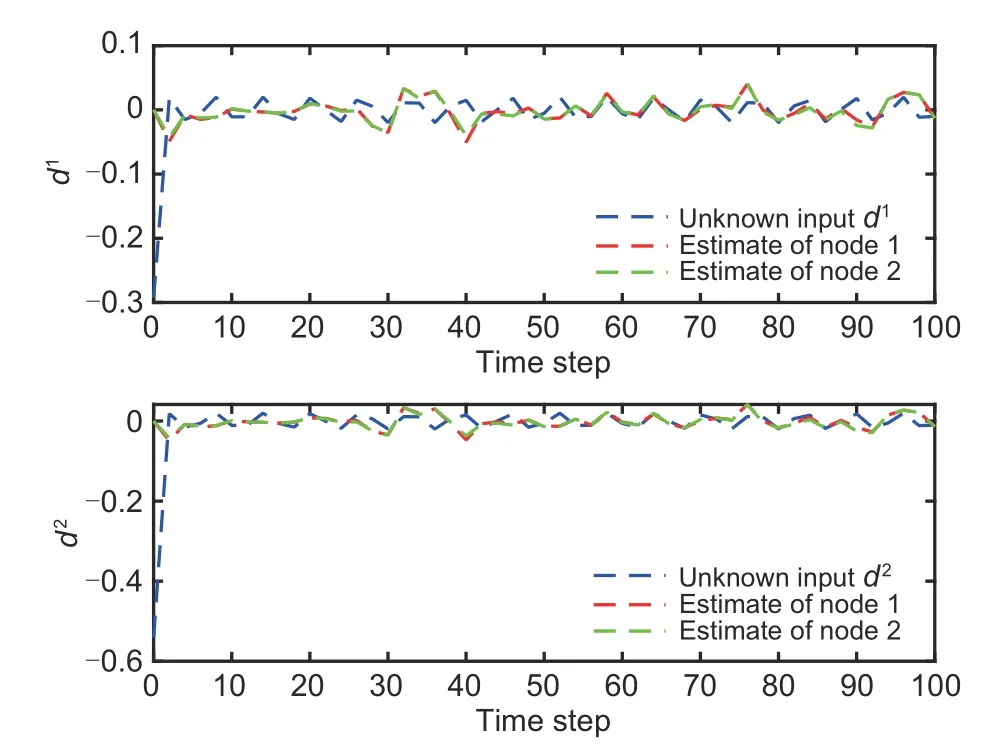



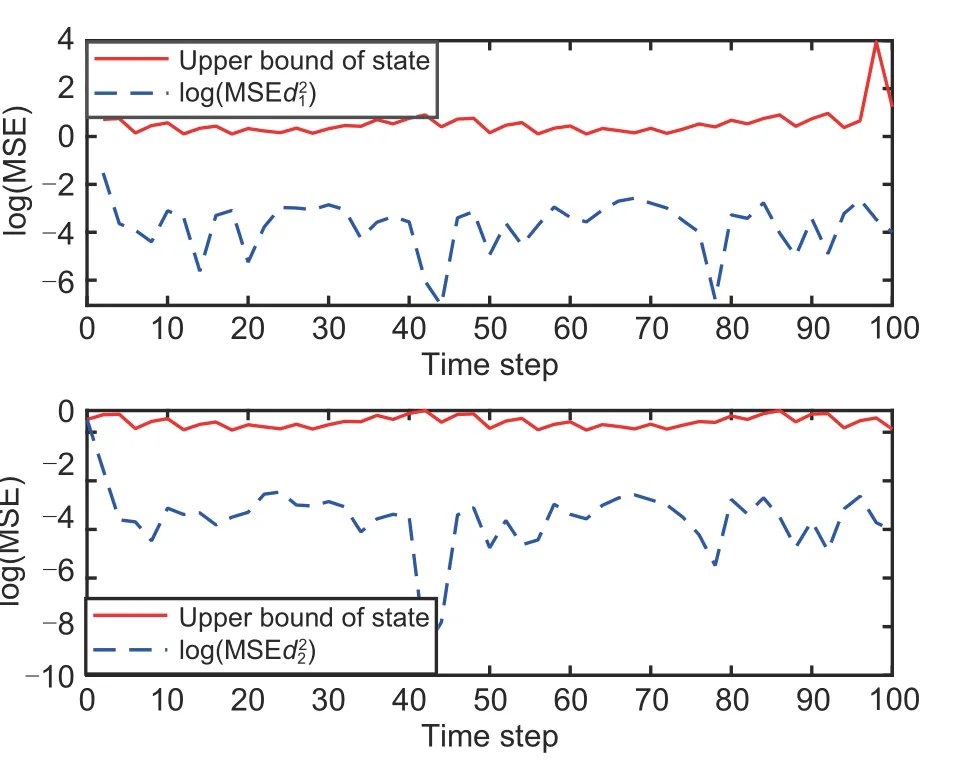

5 Conclusions
杂志排行
Frontiers of Information Technology & Electronic Engineering的其它文章
- Towards resilient average consensus in multi-agent systems:a detection and compensation approach∗&#
- Modified dynamic event-triggered scaled formation control for multi-agent systems via a sparrow search algorithm based co-design algorithm∗
- Event-triggered distributed optimization for model-free multi-agent systems∗#
- Event-triggered finite-time command-filtered tracking control for nonlinear time-delay cyber physical systems against cyber attacks∗
- Outlier-resistant distributed fusion filtering for nonlinear discrete-time singular systems under a dynamic event-triggered scheme∗
- Estimation of Hammerstein nonlinear systems with noises using filtering and recursive approaches for industrial control*
