Modified dynamic event-triggered scaled formation control for multi-agent systems via a sparrow search algorithm based co-design algorithm∗

Yanping YANG ,Siyu MA ,Dawei LI,3 ,Jinghui SUO

1College of Information Science and Technology, Donghua University, Shanghai 201620, China

2Engineering Research Center of Digitized Textile & Apparel Technology, Donghua University, Shanghai 201620, China

3State Key Laboratory for Modification of Chemical Fibers and Polymer Materials,College of Information Science and Technology, Donghua University, Shanghai 201620, China

Abstract: This paper is concerned with the scaled formation control problem for multi-agent systems (MASs) over fixed and switching topologies.First,a modified resilient dynamic event-triggered (DET) mechanism involving an auxiliary dynamic variable (ADV) based on sampled data is proposed.In the proposed DET mechanism,a random variable obeying the Bernoulli distribution is introduced to express the idle and busy situations of communication networks.Meanwhile,the operation of absolute value is introduced into the triggering condition to effectively reduce the formation error.Second,a scaled formation control protocol with the proposed resilient DET mechanism is designed over fixed and switching topologies.The scaled formation error system is modeled as a time-varying delay system.Then,several sufficient stability criteria are derived by constructing appropriate Lyapunov–Krasovskii functionals (LKFs).A co-design algorithm based on the sparrow search algorithm (SSA) is presented to design the control gains and triggering parameters jointly.Finally,numerical simulations of multiple unmanned aerial vehicles(UAVs) are presented to validate the designed control method.

Key words: Scaled consensus;Formation control;Dynamic event-triggered scheme;Switching topology

1 Introduction

With the recent advances in network communication engineering and automatic control technologies,the cooperative control for multi-agent systems(MASs)has attracted ever growing attention because of its wide application scopes in various fields,such as microgrids (Shan et al.,2021;Ning et al.,2023),multi-vehicle systems (Ge et al.,2022,2023;Xie et al.,2023;Zhang XM et al.,2023),wireless sensor networks(Guan and Ge,2018;Ge et al.,2019;Shen et al.,2020),and distributed games (Ye MJ et al.,2023).Specifically,an MAS is usually composed of a mass of distributed agents interconnected through some network medium.Through mutual information exchange and interaction between individuals,MASs can accomplish a large number of complicated tasks that are beyond the capabilities of individual agents(He et al.,2022;Su et al.,2022).The agents in MASs can eventually achieve cooperative goals through collaborative control strategies like rendezvous,target encirclement,formation control,and consensus control(Cao et al.,2013).

In the past years,consensus control has been studied thoroughly in the context of collaborative control of MASs.In common consensus control issues,all agents in an MAS eventually reach the same state.Zhang D et al.(2018) proposed an alternative switched system model to address the consensus problem in heterogeneous linear MASs with nonuniform sampling.Hu et al.(2019) explored the consensus control of high-order MASs with antagonistic interactions and communication noises,where a control strategy employing random approximation was devised by leveraging the information from neighboring agents.Chen et al.(2022) solved the pathfollowing control problem for MASs within finite time.Zhang LZ et al.(2022) investigated the bipartite asynchronous impulsive tracking consensus control for MASs with nonzero leader control inputs.However,in some scenarios,consensus is insufficient to handle complex environments.For example,when aircrafts are searching for targets,the positions of the targets can be determined more effi-ciently through reasonable formation flights.Therefore,formation control,owing to its practical applications,has widely been an area of interest recently.Yu JL et al.(2022) discussed the adaptive optimal time-varying formation tracking control for MASs having a noncooperative leader,and this was achieved in their research through the design of a new formation tracking protocol involving extended state observers and adaptive neural networks.Lin et al.(2014)presented a control protocol based on a complex Laplacian matrix to realize the specified formations using relative positions between agents.Ma et al.(2021) considered theH∞cluster formation problem for MASs under external disturbance and random sampling behavior.Furthermore,in fire rescue operations,firefighters need to be divided into several groups to speed up the rescue,which means that a single formation would be inadequate;accordingly,cluster control and scaled control are introduced into MASs corresponding to such circumstances.There have been numerous research results on cluster control for MASs in the literature.Guo et al.(2021) studied cluster consensus with an event-triggered mechanism for MASs with heterogeneous nonlinear second-order dynamics subject to cyber-attacks.Ge et al.(2018)addressed the cluster formation for MASs subject to aperiodic sampling and transmission delays simultaneously.Scaled consensus means that the states of agents can achieve different consensus according to the pre-determined ratios.In this paper a more practical collaborative control of MASs was investigated through combining scaled consensus and formation control.

The communication among agents in cooperative control of MASs is highly dependent on the underlying network topology.Wang H et al.(2019) investigated the fixed-time consensus problem for MASs with nonlinear first-order dynamics in the presence of directed communication topologies.Huang et al.(2020) designed an innovative control protocol to accomplish the consensus of nonlinear MASs exhibiting second-order kinetics.Luo and Ye(2022)investigated the cluster consensus control for linear MASs without regard to the coupling intensities or connection scenarios.Note that the research outcomes derived in Wang H et al.(2019),Huang et al.(2020),and Luo and Ye (2022) were obtained exclusively under fixed network topologies.However,in some cases,such as when there exist cyber-attacks,the original topology structure has to be changed.In response to the switching topologies,agents need to form new formations to complete the tasks.Meng and Jia (2016) solved the consensus problem of MASs with switching topologies,where all agents agree on a value at different time-varying scales.Zhu et al.(2022) considered the formation control for linear MASs with switching directed topologies by proposing two distributed observer-based event-triggered control mechanisms based on absolute or relative outputs.Dong et al.(2017) discussed the time-varying formation tracking problem of MASs with second-order dynamics.Several sufficient and necessary criteria for the feasibility of formation tracking control were given with regard to switching interaction topologies.

In MASs,the states and control information of agents are exchanged through network transmission with high requirements in terms of network bandwidth and hardware equipment (Wang XL et al.,2022).To maximize the utilization of network resources,an event-triggered scheme was introduced.This scheme ensures that the states and control signals of the agents are updated only when specific conditions are ensured,thereby reducing unnecessary communication.Xu and He (2018) considered the cluster consensus control for MASs with a distributed static event-triggered (SET) strategy.To further achieve the balance between resource saving and system stability,the dynamic event-triggered(DET) mechanism was proposed.It was implemented by introducing an auxiliary dynamic variable(ADV) or a dynamic threshold parameter (DTP).By proposing a distributed DET mechanism involving a DTP,He et al.(2020) studied the consensus problem of linear MASs in leaderless and leader-following topologies under an adaptive control framework.Du et al.(2020)explored the leaderfollowing consensus control in MASs by developing a distributed event-triggered mechanism that incorporates an ADV.Similarly,Ju et al.(2022)studied an ADV-based distributed DET consensus control problem for MASs via fault-estimation-in-the-loop.He and Mo (2022) proposed distributed SET and DET mechanisms for the utilization alleviation of communication resources.The security consensus control for MASs subject to scaling deception attacks was investigated.Note that MASs usually have complex network communication topologies.Thus,it is of significance to explore a better means to balance system stability and network resource saving.

In this study,the scaled formation control for MASs with a modified resilient DET mechanism under fixed and switching topologies is considered.The main contributions are threefold:

1.By introducing a random variable and two different threshold parameters into the traditional DET mechanism,the event-triggering conditions can be adjusted by choosing different threshold parameters according to different statuses of the network,and such an arrangement can enable better use of network resources for the whole system.

2.Different from traditional event-triggered mechanisms where the triggering condition is driven once the combination error term exceeds a certain positive scalar or variable,the absolute value of the combination error term and an ADV are introduced.Thus,the number of event-triggered moments can be effectively reduced and more efficient convergence can be achieved.

3.In the context of MASs with a huge amount of computation,by introducing the sparrow search algorithm (SSA) into the stability criteria for the formation error system in terms of nonlinear matrix inequalities,the control gain can be obtained more reasonably and accurately,thereby reducing the conservatism for control gain design.

2 Preliminaries

2.1 Notations

N denotes the set of non-negative integers.R represents the collection of real numbers.Rnstands for the Euclidean space withndimensions.Rm×nmeans the set of real matrices withm×ndimensions.col{·}represents a column vector.diag(·)denotes a diagonal matrix.⊗is the Kronecker product.C>0 (C ≥0) indicates that matrixCis positive definite (positive semi-definite).INexpresses theN-dimensional identity matrix.1Nstands for anN-dimensional column vector where all elements are 1.sgn[c]means the sign of scalarc.λmin(P)denotes the smallest eigenvalue of matrixP.The superscript T represents the transpose of a matrix or a vector.The asterisk∗indicates the symmetry in symmetric block matrices.||·||represents the Euclidean norm for a vector or matrix.|·|denotes the absolute value for a scalar.E[·] is the mathematical expectation operator.Niis the set of neighbors of theithagent.

2.2 Graph theory

G={V,E,A}refers to a directed graph whereV={v1,v2,···,vN}denotes a set of vertices,E ⊆V×Vindicates a set of edges andA=[aij]∈RN×Nis a weighed adjacency matrix.εij=(vi,vj)∈Esignifies that there exists an edge connectingviandvj,indicating thatvican receive information fromvj.In other words,vjis considered a neighbor ofvi.GraphGis said to be strongly connected if there exists a directed path between each pair of vertices(vi,vj).Fori≠j,if (vi,vj)∈E,aij≠0;otherwise,aij=0.For anyi,aii=0.The Laplacian matrix ofGis defined asL=[lij]∈RN×N,whereliiis the sum of the weights of all edges incident to vertexvi,denoted by,andlijis equal to the negative weight of the edge connecting verticesviandvj,represented by-aijfori≠j.

3 Problem statements

3.1 Agent dynamics

Consider a general linear MAS involvingNagents.The kinetics of theithagent is denoted by

wherexi(t)∈Rnandui(t)∈Rmare the state and the control input of theithagent,respectively.A ∈Rn×nandB ∈Rn×mare real matrices.This paper aims to propose a scaled formation control framework to ensure that each agent’s states in Eq.(1)reach a preset formation according to specified ratios with other agents on its own scale.To do so,the following definitions are presented:

Definition 1(Roy,2015) We set a scale vector=whereαiis a non-zero scalar.For arbitrary initial statesxi(0),the scaled consensus for MAS (1)is achieved if

Definition 2MAS (1) is defined to asymptotically reach scaled formation consensus if

Remark 1According to the above definitions,is established for anyholds.As a result,the scaled formation consensus is achieved eventually.Note that the scaled formation is degenerated to a general formation ifαi=αj.The formation is degenerated as one point iffi(t)=fj(t).In particular,iffi(t)=fj(t)=0,the original scaled formation issue can be reduced to a common scaled consensus problem.

3.2 Modified resilient dynamic eventtriggered mechanism

Fig.1 shows the framework of each agenti.Specifically,the state of theithagent is sampled by sampleriwith a fixed periodh>0 with the sampling sequence{0h,1h,2h,···,ιh,···}(ι ∈N).The sampled statexi(ιh)and its time stampιare encapsulated into a sampled-data packet (xi(ιh);ι) and delivered to the event generator of the neighboring nodes.The triggered states of agentiand its neighbors are transmitted to storeri,and finally sent to controllerito update the control input of theithagent.

Fig.1 Scaled formation control framework for the ith agent

Let us suppose that the triggering sequence for agentiis described as(k ∈N),whereis thekthevent-triggered instant of agentiand=0.The next triggering instantis determined by

whereℓ ∈N,

δi>0,andσi>0.Φ>0 andΩ>0 are the weighting matrices.ei(+ℓh) is denoted as the error variable:

χi()is the accumulated error between agentsiandj,i,j=1,2,···,Nandi≠j,and

ζi(t)is an auxiliary variable satisfying

whereβi>0 andθ1>θ2>0 are positive constants.indicates whether the communication channel of groupis busy–when the communication is busy,=1;otherwise,=0.denotes the group in which agenti(i=1,2,···,N) is located.When agentsiandjare in one group,=.It is obvious that agentsiandjare in the same group whenαi=αj.

Lemma 1For prescribed scalarsδi>0,σi ∈(0,1),andh>0,the auxiliary variableζi(t+ℓh)can be obtained as follows:

Remark 2In traditional DET mechanisms,as a measure of the consensus error,Υiis sometimes positive and sometimes negative.WhenΥiis positive and the event-triggered condition is researched,the states or control information can be updated;whenΥiis negative,the event-triggered condition cannot be met.As a result,the convergence performance of the system is not good enough with a considerable total triggering number.In the modified resilient DET mechanism (4) presented in this paper,by introducing the absolute value ofΥi,the monotonically increasing property can be ensured and the event condition can be triggered when the originalΥiis negative and not triggered.Therefore,the events can be triggered more reasonably and satisfactory convergence performance can be achieved.

Remark 3It is known from Lemma 1 that the smaller the parametersare valued,the easier the event is triggered.In the proposed DET mechanism(4),a random variableis introduced to select two different threshold parameters according to network conditions resiliently.When the network is free,a smaller threshold parameterθ1is chosen and the triggering frequency increases;when the network is busy,a larger threshold parameterθ2is selected and the triggering frequency decreases.The network resources for the whole system can thus be better used.

3.3 Scaled formation control protocol for a fixed topology

In this subsection,a scaled formation control protocol update strategy with the modified resilient DET mechanism(4)is presented for MAS(1):

whereKis the control gain matrix to be designed.Thus,the following closed-loop system can be obtained:

Therefore,the scaled formation error system can be obtained as

4 Stability analysis under a fixed topology

In this section,the stability of error system(14)will be analyzed.

Theorem 1Givenδi>0,σi ∈(0,1),βi>0,θ1>θ2>0,>0,h>0,scale vectorα,and control gain matrixK,system (14) with control protocol(9)and modified resilient DET mechanism(4)is asymptotically stable if there exist matricesR∊>0,Φ>0,Ω>0,andS,such that

ProofSee Appendix A.

5 Scaled formation control protocol for a switching topology

When the MASs are assigned to form several formations to complete complicated tasks,the topology connection may be destroyed due to the varying environment or unexpected incidents such as denial of service (DoS) attacks.The number of groups,the number of agents in each group,and the connection topology need to be re-allocated to cope with the actual situations.In this section,the switching topology caused by DoS attacks obeying the Markov chain(Ye N et al.,2004)is considered.

We setG(ω(t))={G1,G2,···,Gr}(r ∈N)as the set of all possible topologies,whereω(t) is a continuous-time Markov process with its values taken in a finite setR={1,2,···,r}.Π=[ξbd] is defined as the transition rate matrix withb,d ∈R.The transition probabilities can be given by

where Δt>0 and limΔt→0o(Δt).ξbd>0 is the transition rate at which the statebat timetswitches to statedat timet+Δt,andwhenb=d.The corresponding Laplacian matrix is denoted asL(ω(t))={L1,L2,···,Lr}.Then,under the Markov switching topologies and the modified resilient DET mechanism(4),the control protocol is presented as follows:

wheret,andK(ω())is the control gain matrix to be designed.

The error system can be obtained by applying the designed control protocol(18):

The initial condition of the statez(t) is supplied byz(θ)=ψ(θ),θ ∈[-,0] withψ(0)=z(0) andψ ∈Θ,whereΘrepresents the Banach space of absolutely continuous functions [-,0]→RnNwith square-integrable derivatives and the norm

Definition 3(Yu JJ et al.,2009) Under any initial conditions,system(19)is exponentially stable in the sense of mean square,if there exist positive scalarsεandνsuch that

6 Stability analysis under a switching topology

In this section,the stability of scaled formation error system(19)is analyzed.

Theorem 2Givenδi>0,σi ∈(0,1),βi>0,θ1>θ2>0,>0,h>0,Π,scale vectorαb,and control gain matrixKb,system (19) with the proposed control protocol (9) and modified resilient DET mechanism (4) under switching topologies is exponentially stable in the mean square sense if there exist matrices>0,R∊>0,Φ>0,Ω>0,andSsuch that inequality (16)is satisfied and

ProofSee Appendix B.

7 SSA-based control and triggering parameter co-design

It can be seen that matrix inequality (15) in Theorem 1 is nonlinear because of the coupling of variable matricesR1,R3,R4and control matrixK.Similarly,the coupling ofand control matrixKbresults in the nonlinearity in matrix inequality(21)in Theorem 2.One can transform nonlinear inequalities into linear inequalities by applying traditional linearization techniques such as iterative linear matrix inequality (ILMI),cone complementarity linearization (CCL),and the state-space transformation approach,and then calculate the control gain matrix via the MATLAB LMI toolbox.However,on one hand,traditional linearization methods may introduce a certain amount of conservatism,and on the other hand,there may be limited scalability,especially for high dimensions of matrix inequalities for MASs,which usually possess numerous nodes and complex topological connections.Therefore,it is important to develop an effective algorithm to compute the triggering parameters,weighting matrix,and control gain jointly in the context of MASs.

SSA is a nature-inspired optimization algorithm that draws inspiration from the foraging and predator avoidance behaviors exhibited by sparrows(Xue and Shen,2020).Specifically,the sparrows are classified into three categories: discoverer,joiner,and scout.The discoverers,commonly possessing a high fitness value,are in charge of offering fields and directions of foraging for joiners.The joiners monitor and follow the discoverers constantly for earning better food.When the scouts spot predators,they emit warning signals,as a result of which the whole community of sparrows would instantly show predation behavior.The fitness function is designed as the distance between each sparrow and food.The next movement direction of the sparrow group can be determined using the optimal fitness value.This innovative algorithm showcases remarkable optimization capabilities and exhibits high convergence speed.

In this section,SSA is applied to compute the control gain matrix and triggering parameters in the framework of MASs by dealing with the nonlinear inequalities directly.The control gains and triggering parameters are defined as the sparrow positions,and the scaled formation error state is viewed as the fitness value.The pseudo code of the SSA-based control and triggering parameter co-design is shown in Algorithm 1.The following descriptions provide a comprehensive breakdown of the detailed design process: Step 1: initialize parameters.The maximum number of iterations is set as iter and the sparrow cluster size as num.The initial position of the sparrow (i.e.,the control gainK) is randomly selected while the conditions in Theorem 1 or 2 are ensured.

Step 2: design the fitness function.The fitness function is designed as the scaled formation error state for each sparrow.The best position is obtained when the fitness function reaches its minimum value,and the worst position is obtained when the maximum fitness value is reached.

Step 3: update sparrow positions.tis set as the current iteration.denote the positions in thejthdimension in thetthiteration of theithsparrow,which may be categorized variously into discoverer,joiner,and scout,respectively.The updating rules are as follows:

Hereinu ∈[0,1]andρ ∈[0,1]are the stochastic variables for warning;ST∈[0.5,1]is the safety value;μis the stochastic variable obeying the normal distribution;υ ∈R1×dimis the matrix where each element is 1;J+=JT(JJ-1)-1,whereJis a column vector with the same dimension as each sparrow,and the internal elements ofJare composed of 1 and-1;ϖis a random parameter obeying the normal distribution,and refers to the step of position updating;c ∈[-1,1] is a stochastic variable;fidenotes the fitness function of the current sparrow individual;fbandfware the best and worst fitness values,respectively;kbest(t) andkworst(t) are the best and worst positions,respectively;ςis a small constant.

8 Numerical examples

In this section,a simulation platform of a system with multiple unmanned aerial vehicles (UAVs)is set up to confirm the validity of the presented scaled formation control protocols (9) and (18) and the proposed modified DET mechanism(4).

8.1 Multi-UAV system

The kinematic equation of quarotor UAVipresented in Fig.2(the related parameters are described in Table 1)is represented by

Table 1 Parameters of UAV i

Fig.2 Quadrotor UAV schematic

φs=sinφ,φc=cosφ,θs=sinθ,θc=cosθ,ψs=sinψ,andψc=cosψ.

Thus,the decomposition of Eq.(25) in theXandYdirections can be obtained as

Linearization can be performed according to the following principles (Ren and Atkins,2005): (1)Given thatθandφare very small angles,it may be established thatθs≈0,φs≈0,θc≈1,andφc≈1;(2) If the hovering of the UAV is nearly steady,Fi=mig;(3)We may assume that the desired yaw angleψ=0.As a result,Eq.(25)can be rewritten as

whereuxi=-gθanduyi=gφare the decomposition of control input in theXandYdirections (Mahony et al.,2012;Wang JH et al.,2020),respectively.

Thus,the description in Eq.(25) can be linearized as

where⋆representsXorY.p⋆i(t),v⋆i(t),andu⋆i(t)are the displacement,velocity,and control input components for theX(orY)axis,respectively.

We denotexi(t)=col{pxi(t),vxi(t),pyi(t),vyi(t)}andui(t)=col{uxi(t),uyi(t)}.Eq.(27) can be rewritten as

8.2 Scaled formation control under a fixed topology

The scaled formation flying is accomplished if the position states achieve a pre-set formation with a certain scale and the velocity states reach the same value.The underlying topology is illustrated in Fig.3,where an arrangement is presented by which the 12 UAVs are required to take up a threesome formation through the determination of an appropriate scale vector.

Fig.3 Topology G1

Leth=0.01 and=0.5.The formation information and initial states of UAVs 1–12 are given in Table 2.We setζ1i(0)=ζ2i(0)=1.The triggering parametersδi,σi,βi,θ1i,andθ2iare valued in Table 3.The scale vector under the fixed topology is set asα1=By dealing with criteria (15) and (16) in Theorem 1 and the SSA-based co-design algorithm,the triggering weighting matricesandand the control gain matrixcan be calculated.Fig.4 depicts the position trajectories of UAVs 1–12.It is easy to see that the positions of UAVs 1–3 achieve a triangular formation,those of UAVs 4–7 a square,and those of UAVs 8–12 a pentagon.Fig.5 presents theX-andY-axis components of the velocity state responses of the 12 UAVs.Fig.6 plots the sequences of event-triggered moments of UAVs 1–12 based on the modified DET mechanism(4).

Table 2 Formation information and the initial states of UAVi

Table 3 Parameter values

Fig.4 Position states of UAVs 1–12 under G1 (i=1,2,···,12)

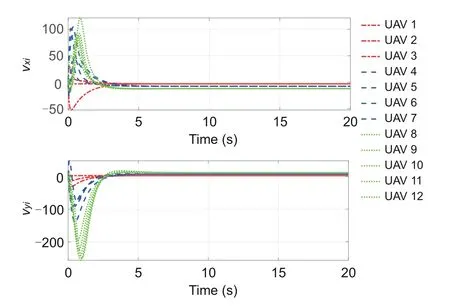
Fig.5 Velocity states of UAVs 1–12 under G1 (i=1,2,···,12)

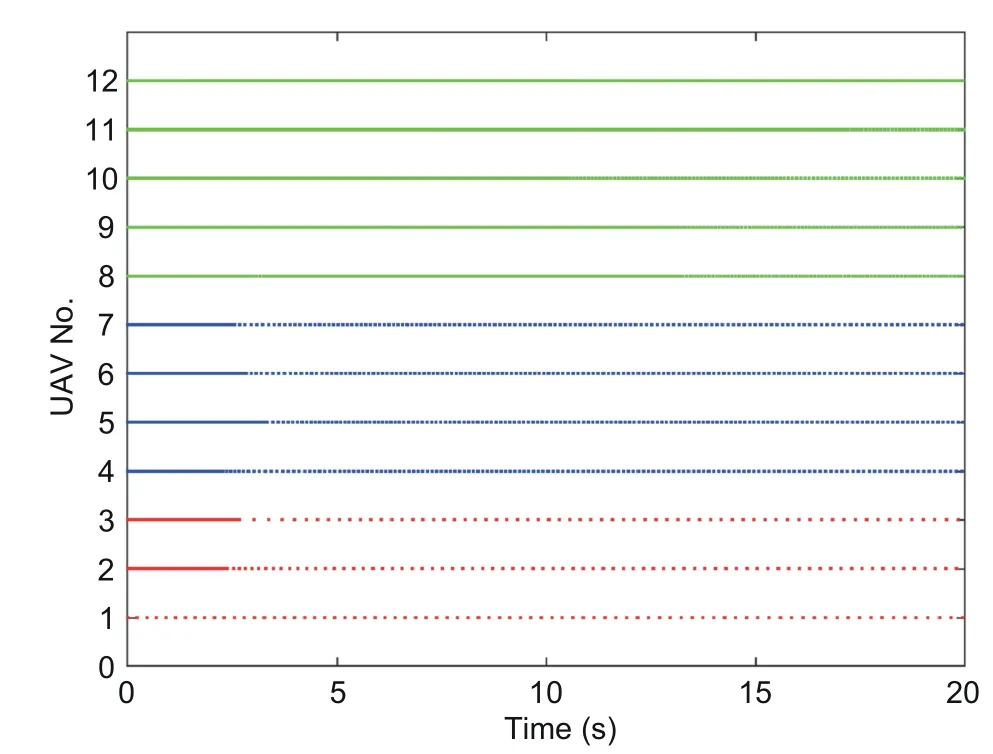
Fig.6 Triggering instant sequences of UAVs 1–12 under G1

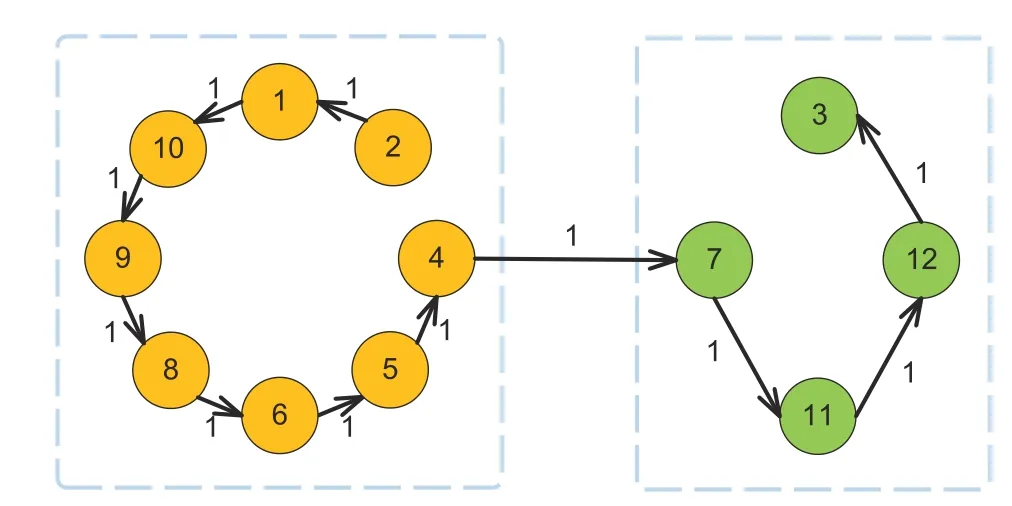
Fig.7 Topology G2

8.3 Scaled formation control under a switching topology

Fig.8 depicts the position trajectories of UAVs 1–12 during the entire running time of 0–20 s.Figs.9 and 10 depict the position trajectories of the UAVs before and after topology switching,respectively.It can be seen that during 0–10 s,the positions of UAVs 1–3 achieve a triangular formation,those of UAVs 4–7 a square,and those of UAVs 8–12 a pentagon.During 10–20 s,the positions of UAVs 1,2,4–6,and 8–10 transform into the formation of a circle,and those of UAVs 3,7,11,and 12 into that of a rhombus.Fig.11 presents theX-andY-axis components of the velocity state responses of the 12 UAVs.Fig.12 gives the triggering sequences of UAVs 1–12 based on the modified DET mechanism(4).

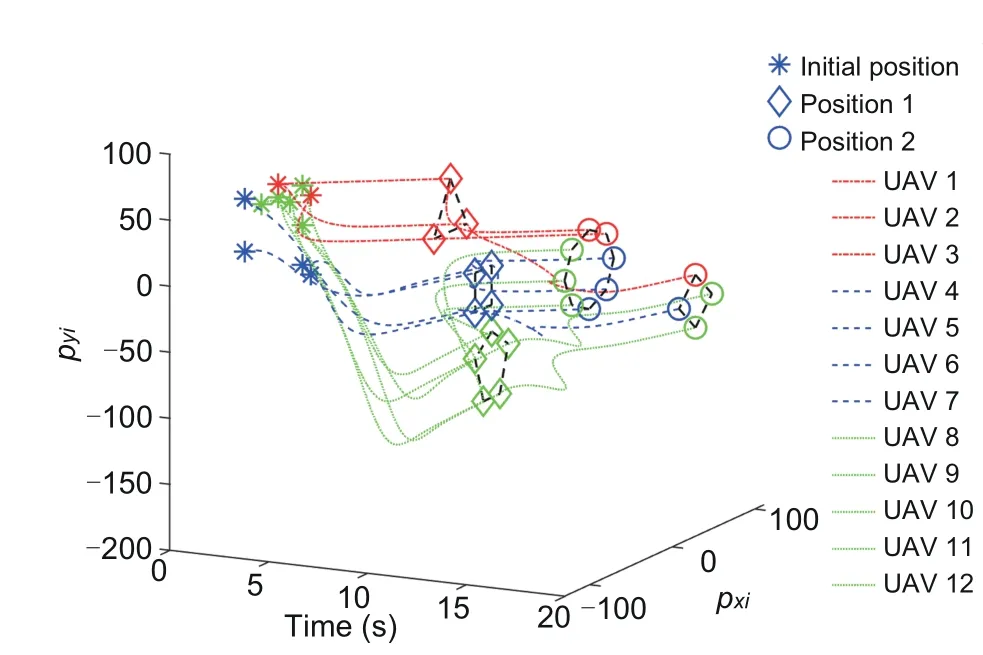
Fig.8 Position states of UAVs 1–12 under G1 and G2(i=1,2,···,12)

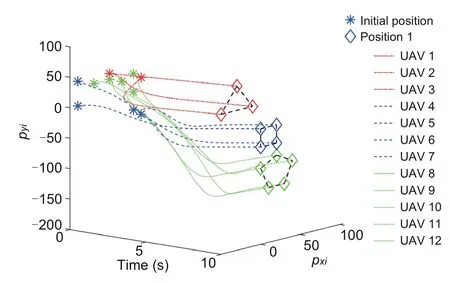
Fig.9 Position states of UAVs 1–12 under G1 in [0,10] s (i=1,2,···,12)

Fig.10 Position states of UAVs 1–12 under G2 in [10,20] s (i=1,2,···,12)

Fig.11 Velocity states of UAVs 1–12 under G1 and G2 (i=1,2,···,12)

Fig.12 Triggering instant sequences of UAVs 1–12 under G1 and G2

8.4 Comparison and discussions

For comparison,four different event-triggered schemes are employed.The total triggering number and errors are obtained and listed in Tables 4 and 5 for fixed and switching topologies,respectively.Table 4 shows that,pursuant to the use of a modified resilient DET mechanism(4)with an absolute value,the required formation control can be reached under a fixed topology with a smaller error,as well as a greater number of instances characterized by a small triggering number.Table 5 shows that the proposed modified resilient DET mechanism (4) exhibits better performance in realizing the expected formation control under a switching topology with a reduced error,while maintaining the same level in terms of the number of instances of triggering.

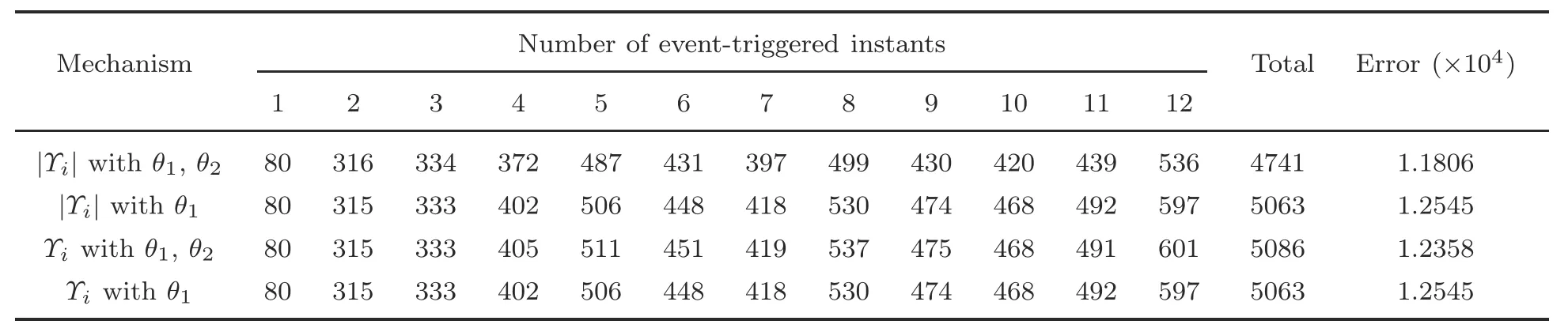
Table 4 Number of event-triggered instants under different mechanisms with a fixed topology for UAVs 1–12

Table 5 Number of event-triggered instants under different mechanisms with a switching topology for UAVs 1–12

9 Conclusions

In this study,the scaled formation control for MASs subject to fixed and switching topologies is investigated.Different from traditional DET mechanisms,a modified resilient DET mechanism based on sampled data with two different threshold values and the absolute value of the combined error is proposed.A scaled formation control protocol is designed by introducing certain formation information,through which agents in an MAS can realize its formation in groups.Then,by choosing appropriate Lyapunov–Krasovskii functionals (LKFs),the stability of the scaled formation error system is verified.Adoption of the SSA algorithm has made it possible to deploy a co-design algorithm through dealing with the derived criteria in terms of matrix equalities,which is essential for the design of the control gain matrix and triggering parameters.In the end,a multi-UAV system is applied as an example for the confirmation of theoretical results.

It is of significance to explore event-triggered cooperative security control for MASs subject to malicious cyber-attacks.An MAS usually consists of a considerable number of nodes distributed in different spatial locations.The nodes in different regions have different network communication conditions;i.e.,the attack type,attack time,and attack intensity may be different.Thus,it is desirable to explore more effective event-triggered security control strategies for MASs in vulnerable networks.

Contributors

Yanping YANG designed the research.Siyu MA drafted the paper.Yanping YANG and Dawei LI helped organize the paper.Dawei LI and Jinghui SUO revised and finalized the paper.

Compliance with ethics guidelines

All the authors declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Appendix A:Proof of Theorem 1

The following Lyapunov–Krasovskii functionals(LKFs)are chosen:

whereU=L+LT>0,R∊>0(∊=1,2,3,4).

Taking the derivative of LKF(A1)yields

By applying a reciprocally convex approach(Park et al.,2011),one obtains

According to the modified DET mechanism(4),the following inequality can be ensured:

Appendix B:Proof of Theorem 2

Appropriate LKFs are chosen as

where>0,R∊>0,∊=1,2,3,4.

We define the weak infinitesimal operatorLofV(t)as

Then one can obtain

By applying a reciprocally convex approach(Park et al.,2011),one can obtain

According to the modified resilient DET mechanism(4),the following inequality is ensured:

In view of inequality (B4),there exists a scalarϖsuch that

For Eq.(B5),we apply the integral from 0 toT>0 on both sides,and calculate expectation

Thus,there exists a scalarϖ>0 such that