Event-triggered distributed optimization for model-free multi-agent systems∗#

Shanshan ZHENG ,Shuai LIU ,Licheng WANG

1College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China

2College of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract: In this paper,the distributed optimization problem is investigated for a class of general nonlinear modelfree multi-agent systems.The dynamical model of each agent is unknown and only the input/output data are available.A model-free adaptive control method is employed,by which the original unknown nonlinear system is equivalently converted into a dynamic linearized model.An event-triggered consensus scheme is developed to guarantee that the consensus error of the outputs of all agents is convergent.Then,by means of the distributed gradient descent method,a novel event-triggered model-free adaptive distributed optimization algorithm is put forward.Sufficient conditions are established to ensure the consensus and optimality of the addressed system.Finally,simulation results are provided to validate the effectiveness of the proposed approach.

Key words: Distributed optimization;Multi-agent systems;Model-free adaptive control;Event-triggered mechanism

1 Introduction

Recently,the distributed coordination of multiagent systems (MASs) has been widely applied in various practical engineering fields,such as smart grids (Mao et al.,2021),automated vehicles (Xie et al.,2022;Ge et al.,2023a;Zhang XM et al.,2023),and distributed filtering (Chen et al.,2022;Liu S et al.,2022).Generally speaking,MASs are composed of interacting individual agents that work collaboratively under certain protocols to handle complicated problems.During the past decades,the analysis,control,and optimization of MASs have emerged as popular research areas and have attracted considerable research attention.Among the research topics of MASs,the consensus is a fundamental problem whose main purpose is to develop some control methods to propel all agents’states to a common value (Chen et al.,2020;Ju et al.,2022;Li and Wei,2022;Zhang QC and Zhou,2022;Ning et al.,2023;Zhang WJ et al.,2023).

For the consensus issue of MASs,it is commonly recognized that the dynamics of agents is available.However,due to the ever-increasing complexity of engineering systems,it is usually difficult and even impossible to establish precise dynamical models of each agent,and this is particularly true for practical MASs that exhibit complicated characteristics including high order,strong nonlinearity,and tight coupling.This gives rise to the model-free MASs whose analysis and synthesis topics have drawn preliminary academic attention.Because the explicit system model is ambiguous and the availability of information regarding system dynamics is confined to merely input/output (I/O) data,the quest for the means to design an effective model-free control approach by using the I/O data is a rather challenging problem.To address this problem,datadriven control methods have been developed in the past decades,among which the model-free adaptive control (MFAC) method is a representative datadriven approach.Different from traditional modelfree methods that require identification of unknown nonlinear models,MFAC employs a novel dynamic linearization technique,based on which the general nonlinear system is equivalently converted into a dynamic linearized model.Owing to their advantages in dealing with the nonlinearities,MFAC algorithms have received ever-growing research interest,with a large number of results both in the theoretical analysis(Hou and Jin,2011a,2011b;Bu et al.,2018;Hou and Xiong,2019;Wang XL et al.,2022;Zhu QM et al.,2023) and practical applications including intelligent transportation (Liu SD et al.,2019),aircraft control (Ye et al.,2022),and medical device control(Fetanat et al.,2020;Pinto et al.,2022).

In certain engineering applications of MASs,we not only are concerned with collaborative behaviors (e.g.,consensus,flocking,and swarming),but also take the economic point of view into account(e.g.,operation cost and resource utilization effi-ciency),which can be concluded as the optimization problem for MASs.The optimization problem for MASs is considered in light of various objectives of individual agents,and the main purpose of adopting this approach is the designing of certain optimization approaches that would enable a globally optimal solution to be achieved.For existing optimization schemes for MASs,there are two representative optimization approaches,namely,the centralized optimization and the distributed optimization.Under the context of the issue of distributed optimization,agents communicate with their neighboring agents by only using the local information exchange and make the optimal decisions through collaborative efforts.Although the centralized optimization scheme might achieve a better performance compared with the distributed optimization approach,it is quite sensitive to network connectivity and is more computationally intensive.When it comes to the case wherein the system scale becomes large,together with the quantum of resources available for computation being limited,such a centralized optimization method is rendered inapplicable.Therefore,the distributed optimization for MASs has been an active research topic that has found extensive applications in parameter estimation of energy configuration(Martins and Oleskovicz,2022;Yu et al.,2022),communication network (Luo et al.,2023;Zhu WB and Wang,2023),and economic dispatch of smart grid(Mao et al.,2021;Wang LC et al.,2022b).

For distributed optimization problems,it is essential to establish an effective optimization algorithm.Moreover,the dynamics of the agents and the corresponding communication topology play a crucial role in evaluating the performance of optimization algorithms.Up to now,plenty of classic algorithms have been devoted to various distributed optimization problems,involving both the undirected and directed communication topologies,and these studies have served as a basis for subsequent works (Nedic and Ozdaglar,2009;Nedić and Olshevsky,2015;Lu and Tang,2012;Shi et al.,2014).In addition,much research effort has been put forward for different types of agent’s dynamical models(e.g.,double-integrator systems,linear systems,and Euler–Lagrangian systems) (Hu et al.,2020;Huang and Meng,2022;Cui et al.,2023).However,the aforementioned results are built on the basis that the dynamics of agents is precise and known a prior,which unfortunately is usually unrealistic to fulfill in practice.As a consequence,how to develop an optimization algorithm without acquiring accurate system dynamics is of both theoretical significance and practical necessity.

It is worth mentioning that for the purpose of achieving certain collaborative tasks,the data exchange among agents is inevitable.However,in numerous practical applications especially for the digital-communication-based MASs,it is often the case that the communication resource is limited,which means that frequent communication is unrealistic (Wang LC et al.,2022a,2023).In this case,it is crucial to alleviate communication burden.Recently,the event-triggered(ET)mechanism has been employed in state estimation/control/optimization problems due mainly to its advantage of efficient resource usage (Ge et al.,2022;Liu ZQ et al.,2022;Ma et al.,2022).A thorough literature search has revealed that the ET scheme has hardly been applied to model-free MASs,not mentioning the corresponding distributed optimization problem,which motivates us to fill this gap.

Building on the aforementioned discussions,in this paper,the ET distributed optimization problem for model-free multiple-input multiple-output(MIMO) MASs has been investigated.This is by no means a trivial task due primarily to the following challenges: (1)How to develop an ET mechanism for the model-free MASs? (2)How to embed the MFAC scheme into the distributed optimization algorithm?(3) How to conduct effective analysis guaranteeing the convergence of the addressed MAS?

In view of the above issues,we endeavor to propose a novel event-triggered model-free adaptive distributed optimization (ET-MFADO) algorithm,by which the consensus performance of MASs is achieved and the optimality of the global objective function is ensured.The main contributions of this study are summarized as follows:

1.A novel ET-MFADO algorithm is proposed to derive the optimal solution of the global objective function for nonlinear MIMO MASs.

2.Compared with existing results,the datadriven ET-MFAC strategy is successfully embedded into the distributed optimization algorithm for model-free-based MASs.

3.Sufficient conditions are established to address the convergence of both the consensus performance and the proposed optimization algorithm.

Notations: Let Rnand Rp×qdenote thendimensional Euclidean space and the set of allp×qreal matrices,respectively.The Kronecker product of matricesAandBis described asA ⊗B.ATrepresents the transpose ofA.ρmin{A}refers to the minimum eigenvalue of matrixA.For a vectorxand a matrixX,‖x‖and‖X‖denote the Euclidean norm and the Frobenius norm,respectively.sign(x) is called a sign function.diag{·}stand for a block-diagonal matrix.A column vectoris defined as colN{ai}.N stands for the set of natural numbers.

2 Preliminaries and problem formulation

2.1 Preliminaries

For any vectorsx,y ∈Rn,functionf(·):Rn →R is called a convex function if the following condition is satisfied:

where∇f(·)∈Rndenotes the gradient of functionf(·).

A weighted undirected graph can be described asG≜{V,E,A},whereV≜{1,2,...,N}is the node set containingNagents,E ⊆ V×Vis a set of edges,andA≜[aij]∈RN×Nrepresents the weighted adjacency matrix of the graph.If agentican acquire information from agentj,it means that there is a path from agentjto agenti,(j,i)∈E,andjis called a neighbor of agenti.The set of neighbors of agentiis denoted byNi≜{j ∈V|(j,i)∈E}.In this case,aij=aji>0 if and only if (i,j)⊆E,andaij=0 otherwise.The Laplacian matrix of graphGis defined asL≜A-D,whereD≜diag{d1,d2,...,dN}is an in-degree matrix with

2.2 Problem formulation

Consider a nonlinear MAS composed ofNagents,in which the MIMO system,given the following,describes the dynamics of agenti:

whereyi(h)∈Rnis the measurement output of agentiwhose value is available at time steph,andui(h)∈Rnis the control input of agenti.gi(·,·):Rn×Rn →Rnis an unknown nonlinear vector-valued function of agenti.

To facilitate our analysis,some assumptions are proposed for nonlinear system(1).

Assumption 1The partial derivative of nonlinear functiongi(x,y) is continuous with respect toy.

Assumption 2System (1) satisfies the generalized Lipschitz condition;that is,for any nonzero vector Δui(h)≜ui(h)-ui(h-1),one has‖Δyi(h+1)‖≤m‖Δui(h)‖with Δyi(h+1)≜yi(h+1)-yi(h)andmbeing a known positive scalar.

Remark 1It should be mentioned that the above assumptions are quite common in engineering applications.In particular,Assumption 1 is actually a mild constraint on the system nonlinearity.The system output signal’s change rate is capped by Assumption 2 at an upper limit,which is a crucial and reasonable requirement for a broad range of practical systems including the MASs (Tan et al.,2022),the interconnected microgrid systems (Zhang HG et al.,2017),and the implantable heart pump systems(Fetanat et al.,2020).

On the basis of the above assumptions,we are in a position to introduce the following valuable lemma,which plays an important role in the subsequent design of the MFAC scheme:

Lemma 1(Hou and Jin,2011a) Given that MAS (1)satisfies Assumptions 1 and 2,if‖ui(h)‖≠0 holds,then system (1) is equivalently converted into the dynamic linearization model as follows:

is called the pseudo-partial-derivative(PPD)matrix and satisfies‖ʊi(h)‖≤m.

With the help of such an equivalent transformation,it is ensured that there is no loss of system information during the linearization process,so that there is no theoretical modeling error between Eqs.(1)and(2).

2.3 Distributed optimization

In this subsection,the distributed optimization problem associated with MAS (1) is formulated as follows:

wherefi: Rn →R is a local convex cost function of agenti,i ∈V.f∗≜minx∈Rn f(x∗) andx∗≜arg minx∈Rn f(x) are defined as the global optimal value of optimization problem (3) and the solution that minimizes the global objective function,respectively.

To guarantee that convex optimization problem(3) has a unique optimal solution,the following assumptions are given:

Assumption 3The gradient of each local objective functionfi(·)is bounded;that is,there exists a positive scalardsuch that fori ∈V,‖∇fi(·)‖≤d.

Assumption 4The diminishing step-sizeα(h) is a positive sequence satisfying the following conditions:

for allh>ς ≥0.

2.4 Event-triggered mechanism

For the sake of saving communication resource,the ET mechanism is employed to reduce the quanta of data necessitated by communication among agents and their neighbors.To be specific,represents the series of triggering instants of agenti,which is iteratively determined by the following rule:

where the event generator functionΓi(ei(h),θi) is defined as follows:

Remark 2To determine whether there prevails a necessity of triggering an event,the controller evaluates,at each operating moment,whether the sampling error surpasses a predetermined threshold.When ET condition (6) is satisfied,the control signal is updated and sent to the actuator to make the error return to zero.Otherwise,the system input remains at its current value.It should be noted that the trigger condition will not continue to be satisfied indefinitely as long as there is a lower bound on the sampling period.As a result,the ET mechanism that has been designed can avoid Zeno behavior.

Before proceeding further,the following definitions and lemmas are introduced first.Denotingby the consensus error of agenti,we then obtain the augmented consensus error dynamics as

Definition 1The closed-loop system(1)is said to be ultimately consensusable,if the augmented consensus error dynamics satisfies

Definition 2The output trajectoriesyi(h) of MAS (1) converge to the optimal solutiony∗if the following condition is met:

Lemma 2(Polyak,1987) Let{t(h)},{π(h)},and{∊(h)}be three nonnegative scalar sequences that satisfy∊(h)≥0,π(h)≤1,and,such that

for allh ∈N.Then,limh→∞t(h)=0.

Lemma 3(Nedić and Olshevsky,2015) Let{ϱ(h)}be a nonnegative scalar sequence.If there exist scalarsϑ(h)≥0,ϕ(h)≥0,andφ(h)≥0 satisfying,such that

for allh ∈N,then the sequenceϱ(h) converges to 0,namely,

Lemma 4(Hardy et al.,1952) Given anyx,y ∈Rn,for any scalarℓ>0,the following inequality holds:

To summarize,the primary goal is to design an MFAC schemeui(h)for MAS(1)under ET communication mechanism (5),in such a way that the following two requirements are simultaneously satisfied:

(1) The closed-loop system (1) is ultimately consensusable;

(2) The output trajectoriesyi(h) of MAS (1)converge to the optimal solutiony∗.

3 Main results

In this section,the ET-MFADO algorithm is proposed by using the MFAC method,considering communication resource constraints.Then,we discuss the convergence of both the consensus performance and the proposed optimization algorithm for MAS (1).

3.1 Algorithm design

1.The traditional distributed MFAC.In engineering practice,it is usually difficult to determine the exact value ofʊi(h)in Eq.(2).Thus,an alternative way is to develop a certain estimation algorithm to obtain an estimate ofʊi(h)by using the I/O data(i.e.,ui(h) andyi(h)).In this sense,the following distributed MFAC scheme is designed:

The following performance index functions are introduced:

We differentiate Eqs.(12)and(13)with respect to(h) andui(h),respectively,and let them equal to 0.

Then,we have

Remark 3It follows from Lemma 1 that nonlinear MAS (1) can be converted into linearized model (2).Moreover,the update of parameter estimate (14) and control scheme (15) are obtained by minimizing two performance indicators that have been defined in Bu et al.(2018).For details,readers can refer to Bu et al.(2018) and the references therein.

2.The ET-MFADO.To better study the distributed optimization problem,we introduce a gradient variable for control inputui(h).The ETMFADO algorithm is given as follows:

3.2 Consensus analysis

At the level of MASs,some system states can be described as the following column vectors:

ξi(h),in the research of MASs,represents the state information that can be obtained from each agent and the neighboring agents,as expressed by the following:

In combination with Eq.(6),one can deduce that

Then,Eq.(21) can be reformulated as the following form:

whereLis the Laplacian matrix andInis ann×nidentity matrix.

In what follows,from Eq.(2),the average consensus error is reformulated as

According to control input update algorithm(18),Eq.(23) can be reformulated as

By means of augmentation operation,one obtains the following compact system:

In the following theorem,the consensus of error system(25)with the proposed MFADO algorithm is investigated:

Theorem 1Given Assumptions 1 and 2,let scalarsν,μ>0,τ,λ,γ ∈(0,1),and matrices,,andbe known.MAS (1)is ultimately consensusable under the proposed algorithm in Eqs.(16)–(18) if there exist positive scalarsε1–ε3andℓ1–ℓ6satisfying

ProofThe proof of this theorem is provided in the supplementary materials.

3.3 Optimality analysis

After setting the consensus criterion for MAS (1) in Theorem 1,in this subsection,our primary attention will be focused on the distributed optimization problem (3).Based on the results obtained in Theorem 1,we aim to provide a suffi-cient condition for ensuring that the convergence of the output trajectories of MAS (1) is in an optimal manner.

Defining the optimization errorcolN{y∗},andδ(h) ≜yd(h)-,based on the boundedness ofyd(h) and,it can be found that there exists a positive scalarlsuch that‖δ(h)‖ ≤l.In terms of Lemma 1,the transformed form of the optimization error dynamics is presented below:

According to the control input update algorithm(18),it is reasonable to reformulate Eq.(27)toward the following compact form:

Theorem 2Given Assumptions 3 and 4,let scalarsν,μ>0 and 0<λ,γ<1 be known.The output trajectoriesyi(h)of MAS(1)converge to the optimal solutiony∗under the proposed algorithm in Eqs.(16)–(18) if there exist positive scalarsω1–ω3andℓ7–ℓ12satisfying

ProofThe proof of this theorem is provided in the supplementary materials.

Remark 4So far,we have addressed the distributed optimization problem for model-free MASs under the ET mechanism.Compared with extensive literature,our main results exhibit the following two distinguishing features: (1) The designed ETMFADO algorithm is novel since the data-driven ETMFAC strategy is taken into account for model-freebased MASs;(2)The proposed algorithm can ensure the convergence of both the consensus and optimality performance under unknown model frameworks.

4 Simulation

In this section,a simulation example is executed to verify the validity of the provided ET-MFADO algorithm.This example focuses on a MIMO MAS composed of four agents,where each agent’s dynamics is expressed as follows:

Agent 1:

Agent 2:

Agent 3:

Agent 4:

uij(h) andyij(h) (i=1,2,3,4,j=1,2) represent thejthinput and output of theithagent,respectively.

It is worth noting that the mathematical models of the agents are unknown and the aforementioned model is used merely to produce I/O data.The communication topology of the addressed MAS is displayed in Fig.1,and the following corresponding adjacency matrix is given:

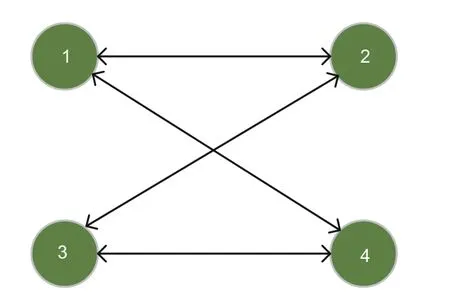
Fig.1 The topology graph of the communication network

In this example,the controller parameters and the initial states are chosen asλ=0.001,μ=0.5,ν=0.8,γ=0.5,ρ=0.1,m1=0.1,m2=0.5,a=2,c=0.5,uij(1)=0,and(1)=[0.5 0.01;0.01 0.5].The trigger condition and the diminishing step sizes are set asθ=0.008,

For the given MAS,the optimization problem can be depicted as follows: miny∈R2f(y(h))=,where the local objective function of each agent is represented byfi(y(h))=zi‖y(h)-yi‖withz1=1,z2=11,z3=6,z4=4,y1=[0.5 0],y2=[1 2],y3=[1 0],andy4=[-0.5 0].By means of MATLAB software,we obtain the optimal solution to the convex optimization problem asy∗=[1 2]Tand the global optimal value isf∗=24.0616.

The specific simulation results are displayed in Figs.2–8.The average consensus error and the output trajectories of the system are given in Figs.2–5.It is clearly visible that the consensus error is convergent and that the trajectories of the output signalsyi(h) asymptotically converge to the optimal solution.Fig.6 describes the error trajectories between the output and the optimal solution.Fig.7 shows the error betweenf(y∗) andFurthermore,the triggering constants of the proposed ET scheme are presented in Fig.8.Obviously,when the ET scheme is employed,there is a perceptible reduction in the control update frequency,resultant to which the communication burden is alleviated.

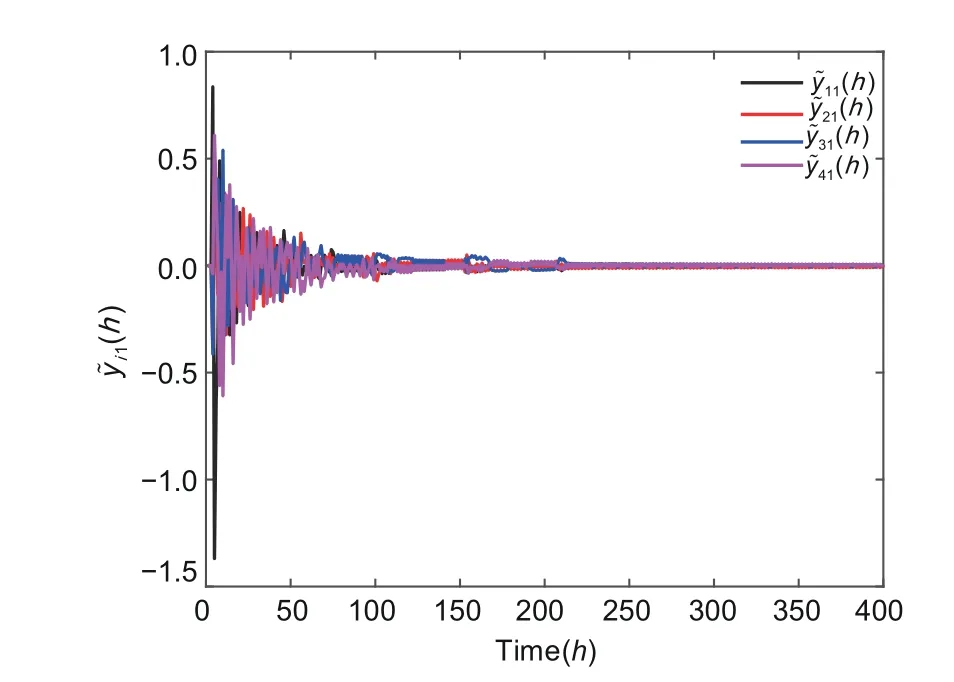
Fig.2 The first component of the average consensus error (h)

Fig.3 The second component of the average consensus error (h)

Fig.4 Output trajectories of yi1(h)

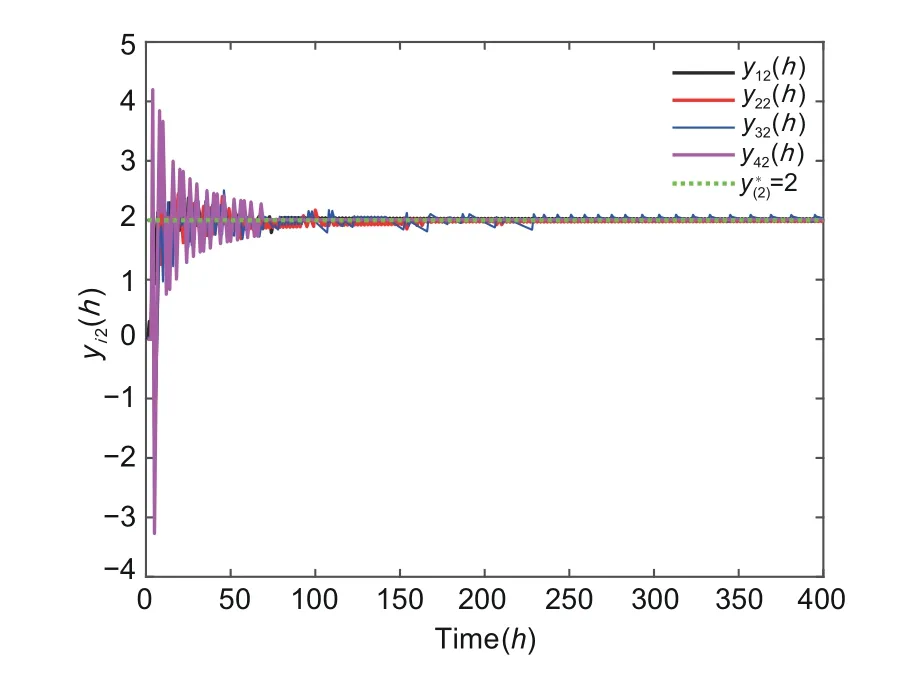
Fig.5 Output trajectories of yi2(h)

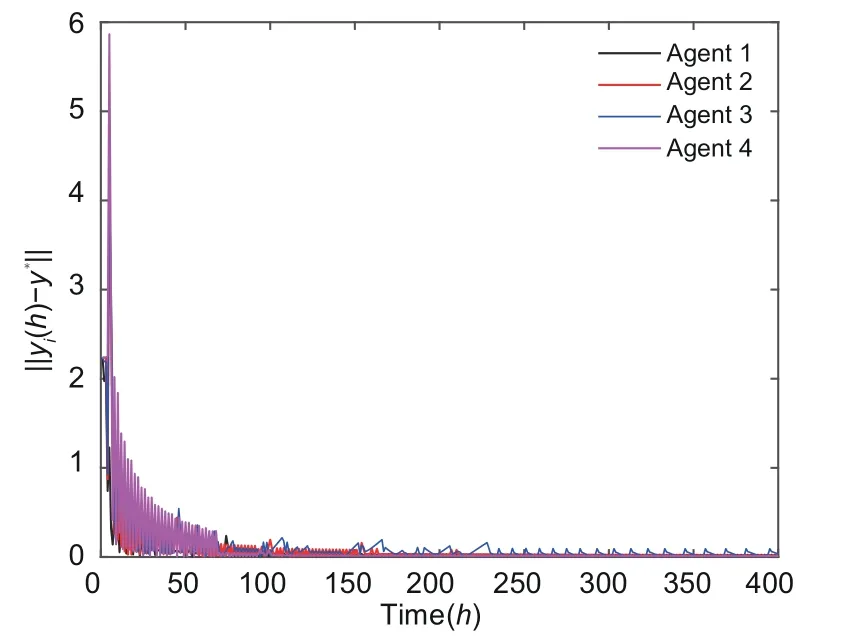
Fig.6 Evolution of the output error ‖yi(h)-y∗‖

Fig.7 Error of the optimal value|f(y∗)-=1 fi(yi)|

Fig.8 Trigger time of each agent

5 Conclusions

In this paper,a novel ET-MFADO algorithm has been proposed to handle the distributed optimization problem for unknown nonlinear MASs under the ET mechanism.The dynamical linearization technique has been employed to equivalently convert the general nonlinear system into a dynamic linearized model,which overcomes the limitation of unknown models.An ET mechanism has been presented to reduce the network communication burden and improve system performance.Some sufficient conditions have been implemented for the closedloop system to achieve the required performance in light of the Lyapunov theory.Finally,a simulation example has been used to verify the effectiveness of the provided algorithm.Future research topics will extend our results to the model-free-based MASs with time-varying communication topology or the various practical engineering fields,such as multirobot navigation(Chang et al.,2023)and automated vehicles(Ge et al.,2023b).

Contributors

Shanshan ZHENG designed the research and drafted the paper.Licheng WANG helped organize the paper.Shanshan ZHENG and Shuai LIU revised and finalized the paper.

Compliance with ethics guidelines

Shanshan ZHENG,Shuai LIU,and Licheng WANG declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

List of supplementary materials

1 Proof S1 Proof of Theorem 1

2 Proof S2 Proof of Theorem 2