逆向思维在初中物理解题中的应用

余里

【摘要】初中物理学科知识具备复杂性、抽象性等特征，对应题型难度较高，复杂多变，考查学生的综合实践能力.要想提高学生的物理解题能力，就要摒弃过去的题海战术，不断完善学生的物理思维，引导学生从不同角度思考问题，进而总结解题经验，能够举一反三.本文主要分析逆向思维在不同物理题型中的应用策略，以期能够优化当前初中物理解题教学的现状.

【关键词】逆向思维；解题方法；初中物理

1 利用逆向思维解答初中物理中的运动问题

例1 目前有一辆货运车中装满了送往灾区的救济物资，已知这一货运车在装满货物后的重量为35000N，且这一满载货车正在水平路面上以10m/s的行驶速度运动，那么在它运动10min后，测量发现当前货车行驶中受到的阻力数值为3000N，请大家计算这一货运车在行驶的10min中牵引力对货运车做功的大小？并计算出货车的功率是多少？

解析 这一物理试题属于十分典型的物理运动问题，然而如果学生按照正常思维来进行解答，那么极有可能受到“货运车在装满货物后的重量为35000N”这一已知条件的影响，从而得出错误答案.实际上，我们在解答类似的物理运动问题时并不需要使用上述条件进行分析.物理教师可以引导学生采用逆向思维进行探究，具体为：学生首先能够运用课堂所学的距离公式（s=v×t）来计算货车的运动距离.已知条件中指出货车行驶了10min，因此这一段时间内货车的距离就是：10×60s×10m/s=6000m.题干中指出货车始终为匀速行驶，因此我们能够根据所学知识“力的作用是相互的”来得出如下结论：货车行驶中受到的阻力数值与其承受的牵引力数值保持一致，因此：F=f=3000N，那么我们就能够求得牵引力对货车做功为：W=Fs=3000N×6000m=1.8×10J，进而计算出其相应的功率数值为：P=W/t=30000W=3×10W.

思考 在对此类物理题型进行教学时，授课教师应当带领学生运用逆向思维进行探究，引导学生规避题干中的干扰信息，并运用有效的已知条件来进行逆推，最终正确发现阻力、牵引力以及功率他们间的内在关联.物理教师应当带领学生进行专题训练，从而提高初中学生分析问题、解决问题的效率.

2 利用逆向思维解答初中物理中的磁场问题

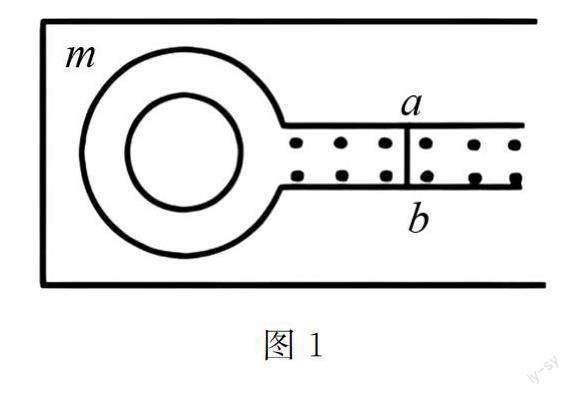
例2 如图1所示，现将一个能够忽略电阻的平行金属导轨放置在匀强磁场内，且导轨与大线圈m二者始终处于连接状态，已知导轨上方放置了一条裸体导线ab，那么此时应当怎样移动导线ab的位置，才能够保证大线圈m内的闭合线圈可以产生顺时针方向的感应电流呢？

解析 例题2属于十分常见的物理磁场题型，能够考查初中学生对“磁场电流形成原理”相关知识的掌握情况，并了解学生对于电流方向和磁场方向的辨别能力.如果依据正向思维来解答这类题型，学生则会在探究中使用常见的右手法则，通过导线移动的已知条件来进一步辨别磁感电流的方向.但是如果使用逆向思维来进行解答，那么学生就能够逆向使用右手法则来快速得出ab的移动方向，本题答案为向右.

思考 例题2乍一看较为简单，但是却是一道能够借助逆向思维解决物理磁场问题的典型题目，学生在解题训练中能够不断完善自身的逻辑思维，并有效提高自身解决问题的能力.

3 利用逆向思维解答初中物理中的浮力问题

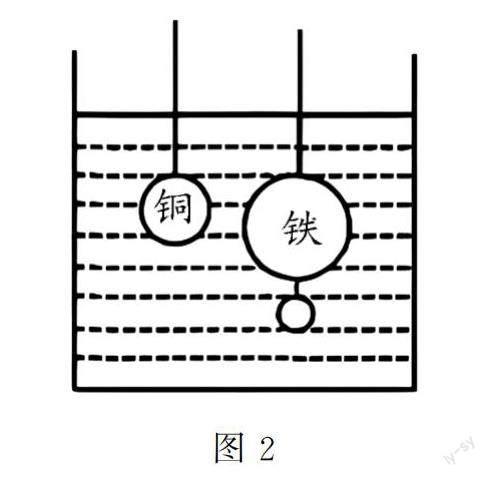
例3 如图2所示，现将两个实心小球（一个铁质、一个铜制）放入盛满清水的容器内，并分别通过一根细线悬挂于同一类型的弹簧测力计上，在不考虑细线质量与体积的情况下，两个实心小球在清水内的弹簧测力示数相等.当我们将两个小球拿出水面后，哪个小球的弹簧测力数值较大呢？

解析 这一道物理题向学生展示了一次较为繁琐的测力实验过程.学生虽然能够在阅读中了解到测力的整个流程，但却不知如何分析拿出水面后两个实心小球的质量.授课教师就可以带领学生采用逆向思维进行解答，根据题干已知信息来设计一个相反的物理实验：若存在两个实心小球，他们在拿出水面后测量的重量数值相等，那么我们就可以根据浮力公式：F=ρgV了解到，体积更大一些的实心铁球所受到的浮力数值会更大.那么为了能够确保两球在清水内弹簧测力示数相等，就应当给铁球悬挂更多的物体以增加重力.上述环节就是运用逆向思维进行探究，若两个测力计显示的数值相同，那我们将两个实心小球提出水面后，铁球的测力数值会更大一些.

思考 物理教师应当带领学生灵活借助逆向思维来简化解题流程，深度扩展学生的物理解题思维，充分提升学生的解题效率.

例4 现存在一个玻璃瓶，其内未放置任何物品，我们将这一瓶子密封后插入装满清水的容器内，并发现这一玻璃瓶恰好能够悬浮在清水中.假设该玻璃瓶的密度为2.5×10kg/m，请大家计算玻璃瓶容积与瓶中空气的比值.

解析 在解答这一道物理浮力题，大多数初中学生会使用正向思维进行解答，即：由已知信息得知玻璃瓶能够恰好悬浮在清水中，因此我们能够假设此时水的密度和玻璃瓶密度均为1，那就意味着玻璃瓶本身以及其内部空气的整体密度为1，这时我们可以假设玻璃瓶的总体积数值为V，而瓶内容积数值为V，且玻璃与水二者密度分别为ρ与ρ，那么我们就能够列出以下式子：ρV－ρV=ρV，將已知条件代入后我们就能够得出正确答案即：2.5∶2.除了能够使用正向思维进行解答，物理教师还可以带领学生运用逆向思维进行探究，即根据密度公式进行逆推，再借助二力平衡的相关物理知识来列式求解，解题流程与正向解题一致.

思考 大多数初中学生均能够运用正向思维解答物理问题，若授课教师能够引导学生灵活使用逆向思维进行分析，那么学生就能够根据问题来逆推解题需要的条件，进而有效简化解题流程，快速得出正确答案.

4 结语

通过上述的分析能够发现，逆向思维能够帮助初中学生快速解决疑难问题，有效提高学生的物理实践运用能力.在面对一些复杂的浮力问题、电学问题、电磁问题以及运动问题时，授课教师需带领学生采用逆向思维进行分析，不断加强学生使用逆向思维解题的能力.

参考文献：

[1]张永虎.逆向思维在初中物理解题中的运用探析[J].数理化学习（教研版），2023（05）：12-14.

[2]陈晶.深化知识理解 培养逆向思维——核心素养下初中物理逆向教学实践策略[J].数理化解题研究，2022（32）：74-76.

[3]李军.逆向思维应用于初中物理教学中的路径探寻[J].名师在线，2022（21）：46-48.