基于垂荡和纵摇运动模型对波浪能最大输出功率的设计

李勇达，汪恒恺，李鹏辉，陈昊

基于垂荡和纵摇运动模型对波浪能最大输出功率的设计

李勇达，汪恒恺，李鹏辉，陈昊

（淮北师范大学 数学科学学院，安徽 淮北 235099）

研究波浪能装置最大输出功率的设计，以运动平衡方程和能量输出系统研究为基础理论背景，建立浮子和振子的垂荡、纵摇运动模型和最优阻尼系数模型，确定给定时间下的浮子与振子的垂荡位移及速度和纵摇位移及角速度，并借助模拟退火算法和网格搜索算法分别确定两种情况下给定参数值的最大输出功率及最优阻尼系数．

波浪能；最大输出功率；垂荡和纵摇运动模型；模拟退火算法；网格搜索算法

随着经济和社会的发展，人类面临能源需求和环境污染的双重挑战，发展可再生能源产业已成为世界各国的共识．波浪能具有可再生、清洁等特点，且相较于风能和太阳能，波浪能具有更大的能量密度[1]．自20世纪70年代开始，英国、挪威、日本、葡萄牙和中国等国家开始重视波浪能的研究，已发明了各种各样的波浪能转换装置，波浪能装置的能量转换效率是波浪能规模化利用的关键问题之一．

本文所研究的波浪能装置见图1～2（来源于2022年高教社杯全国大学生数学建模竞赛题目[2]）．图1装置由浮子、振子、中轴以及能量输出系统（PTO，包括弹簧和阻尼器）构成，振子、中轴及能量输出系统被密封在浮子内部，浮子由质量均匀分布的圆柱壳体和圆锥壳体组成，两壳体连接部分有一个隔层，作为安装中轴的支撑面．振子是置于中轴上的圆柱体，通过能量输出系统与中轴底座连接．在波浪的作用下，浮子运动并带动振子运动，通过两者的相对运动驱动阻尼器做功，并将所做的功作为能量输出．

图2装置在图1装置的基础上，扩充了能量输出系统，除了直线阻尼器，在转轴上安装旋转阻尼器和扭转弹簧，直线阻尼器和旋转阻尼器共同做功输出能量．同时，振子随中轴转动，沿中轴进行滑动．扭转弹簧的扭矩与浮子和振子的相对角位移成正比．旋转阻尼器的扭矩与浮子和振子的相对角速度成正比，比例系数为旋转阻尼器的旋转阻尼系数．

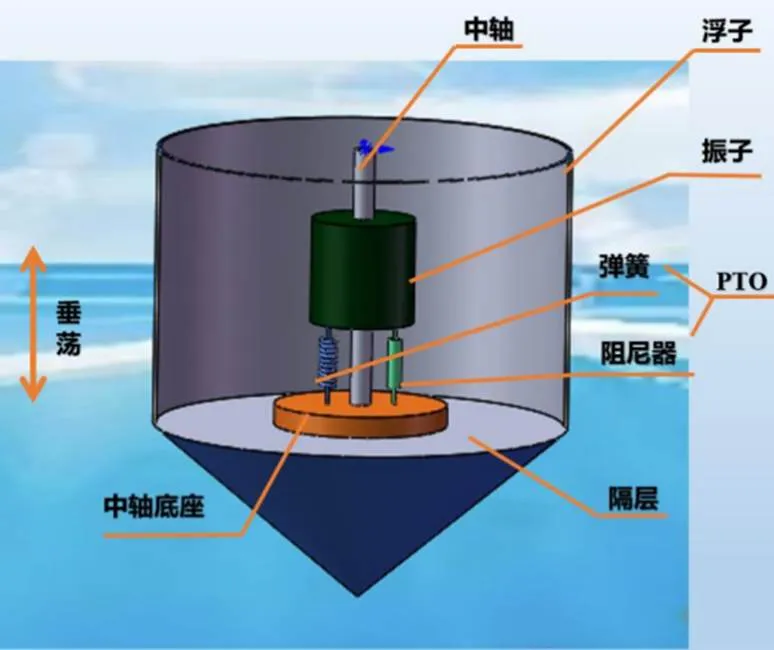
图1 波浪能装置

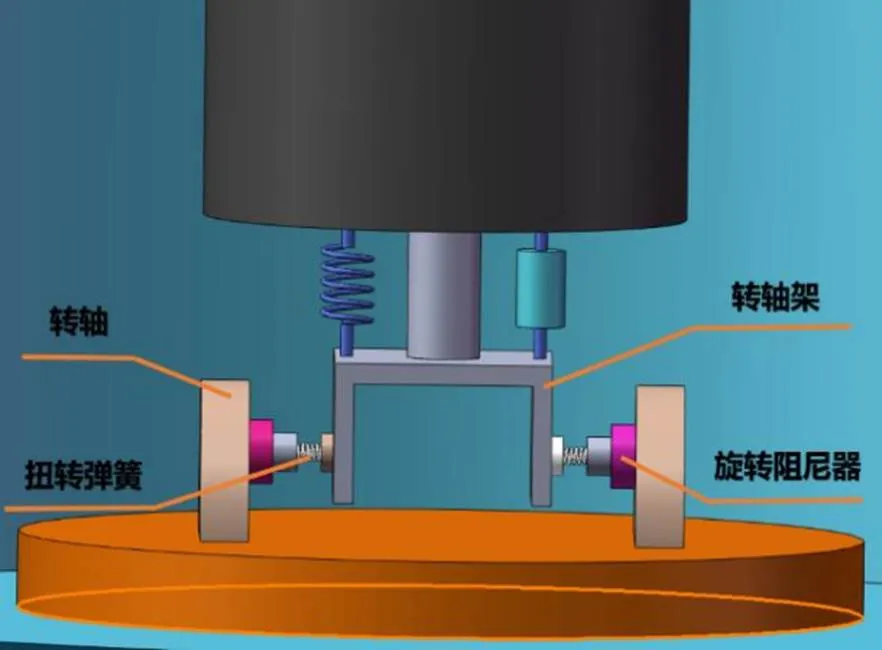
图2 改造后的波浪能装置

本文根据图1～2计算浮子和振子在波浪激励力作用下前40个波浪周期内时间间隔为0.2 s的最大输出功率及相应的最优阻尼系数，建立相应的数学模型，使得能量输出系统的平均输出功率最大．

1 基于浮力摆式波浪能运动平衡方程的垂荡和纵摇运动模型

1.1 浮子的运动方程

在垂荡运动状态下，浮子与振子相对运动，对阻尼器做功，最终将波浪能转化成可用能量[3]．本文假设海水是无粘及无旋的，且海面上除浮子装置外无其他漂浮物，忽略中轴、底座、隔层及能量输出系统的质量和各种摩擦，假设初始时刻浮子和振子平衡于静水中且忽略海风等因素对装置的直接影响．

考虑浮子只做垂荡和纵摇运动，根据CFD方法[4]可将纵摇和垂荡的浮子运动模型表示为

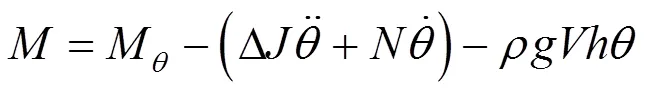
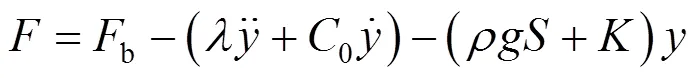
当忽略非线性因素时，可以得到浮力摆的线性运动方程式[5]

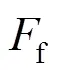
1.2 浮子与振子系统的联合运动方程

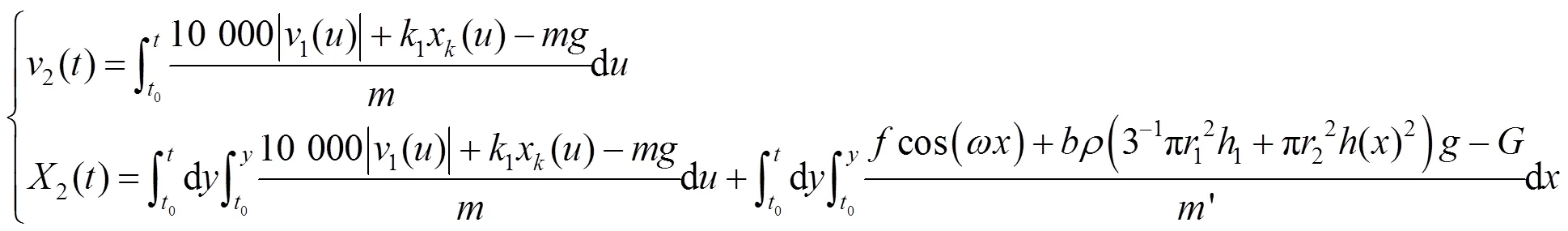
1.3 模拟退火算法

对于浮子、振子系统在最大平均功率下对应的阻尼系数问题，采用模拟退火算法，它基于蒙特卡洛迭代法，采取Metropolis接受准则，是局部搜索算法的拓展，以一定的概率选择领域中目标值较大的状态，从而达到全局优化的目标[6]．

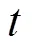
Step3 对解进行迭代求值，随着迭代次数的增加，将会有越来越多的解不被接受．

Step4 结束迭代．当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可．若出现过多解不被接受则结束迭代．

1.4 平均功率最大的优化问题

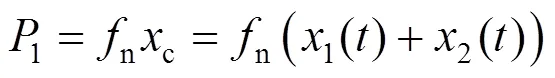
2 双阻尼器下的多变量功率优化模型

2.1 建立双阻尼器下的纵摇与垂荡模型

以平衡位置为初始位置，此时浮子与振子都在垂直位置，浮子的垂荡运动状态同上，对浮子的纵摇运动状态进行受力分析（见图3）．

图3 浮子受力分析

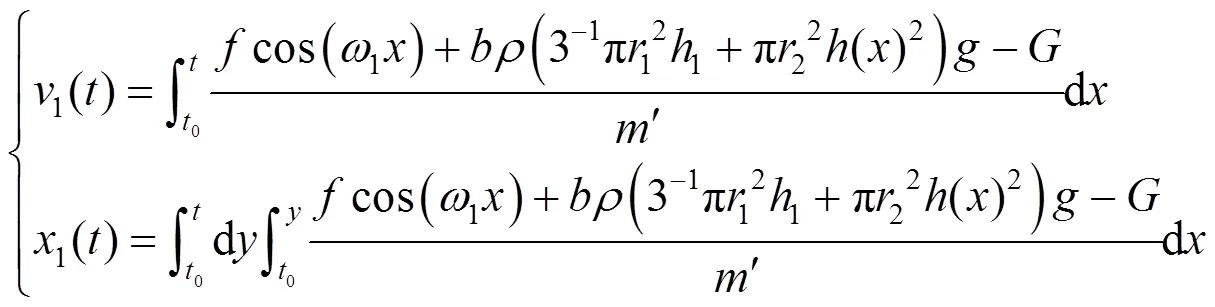
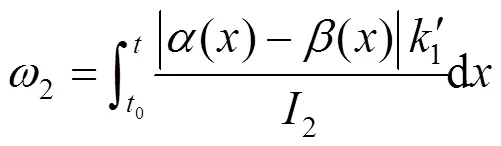
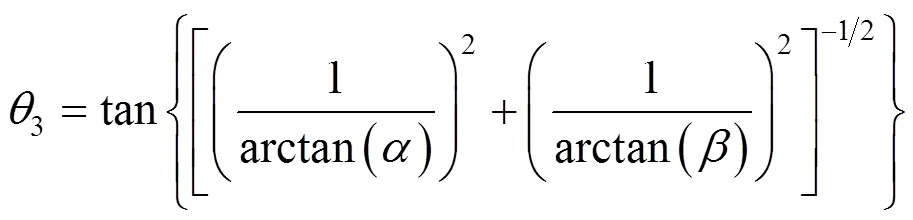
振子的联合运动方程为

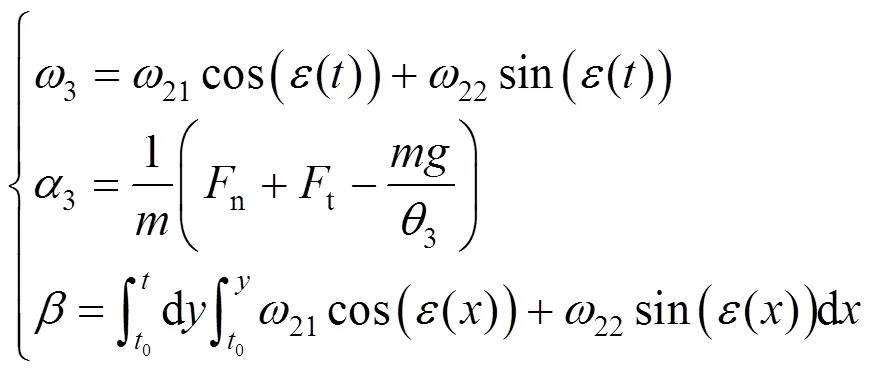
2.2 PTO阻尼数学模型

2.3 双阻尼器下的最优功率

在所建模型基础上求解最优直线阻尼系数和旋转阻尼系数，同时计算最大输出功率及相应的最优阻尼系数，能量主要来自直线阻尼器和旋转阻尼器做功[8]，结合式（9）～（11），可得系统功率表达式为

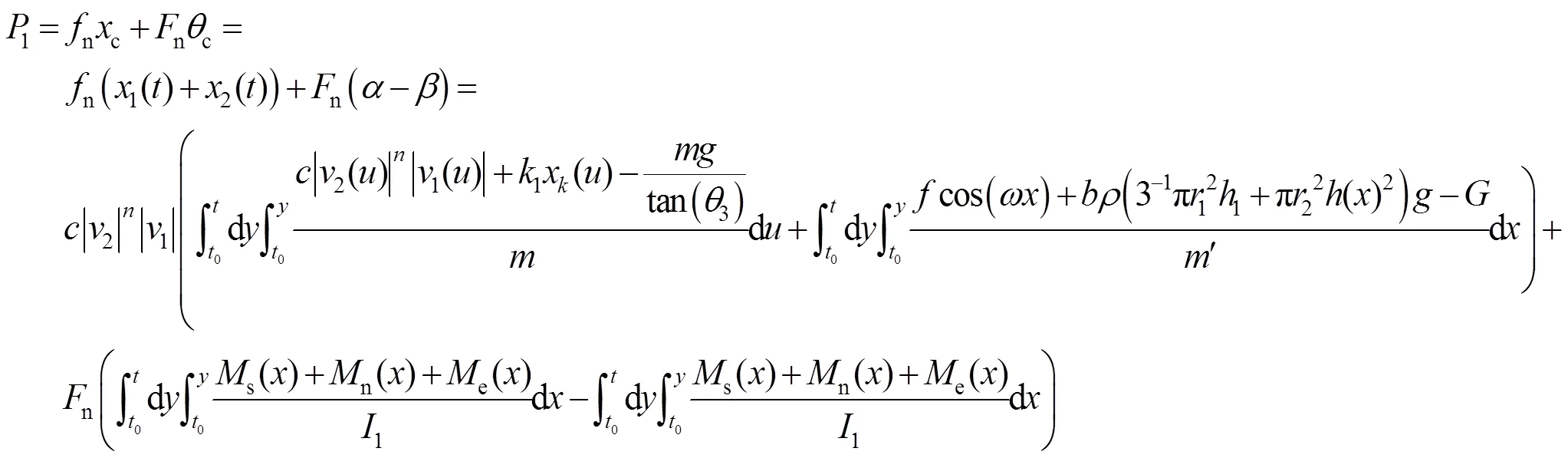
3 数据的整合与处理

3.1 阻尼器下运动状态与最优功率

分析浮子的运动位移，将数据代入模型公式并进行二次积分，求得10，20，40，60，100 s时（1）阻尼系数为常量；（2）阻尼系数与浮子和振子的相对速度的绝对值的幂成正比两种情况下浮子和振子的垂荡位移与速度（见表1）．

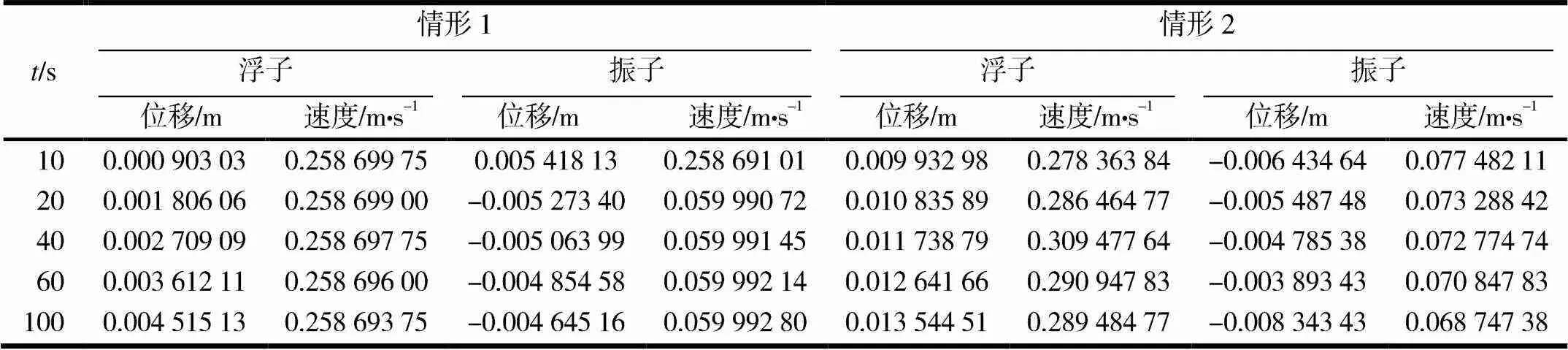
表1 两种情况下浮子和振子的垂荡位移与速度

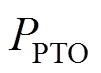
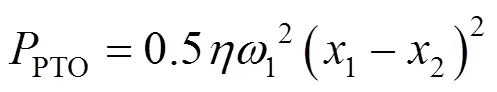
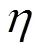
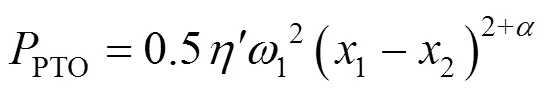
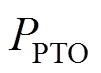
3.2 双阻尼器下运动状态与最优功率

利用PTO阻尼数学模型[9]结合双阻尼器下的多变量功率优化模型，代入相关参量，化简得到浮子的垂荡运动方程为

浮子的纵摇运动方程为

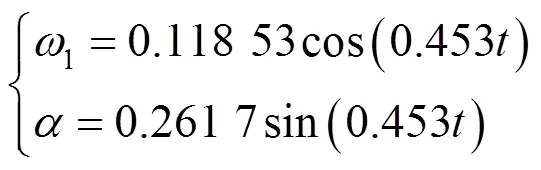
振子的垂荡运动方程为

振子的纵摇运动方程为

由式（15）～（18）可得到10，20，40，60，100 s时浮子与振子的垂荡位移、垂荡速度和纵摇角位移、纵摇角速度（见表2）．

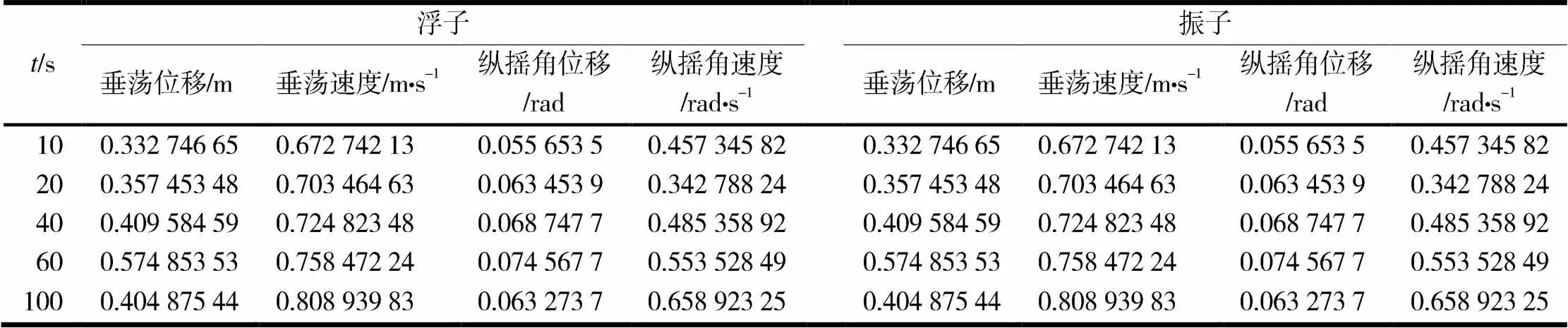
表2 浮子和振子的垂荡位移、速度及纵摇角位移、角速度

当振子和浮子在双阻尼器下运动时，难以得到解析解，因此采用网格搜索法进行迭代搜索，进而得到最优数值解．

在较大范围内采用较大步距对能量输出系统中在双阻尼情况下最大功率进行粗搜[10]，让两个参数在符合实际且上文所给出的范围内划分网格形成网点，并且对划分的网格点进行遍历，求各网点的目标函数值和约束函数值，对可行点比较目标函数值的大小选其中最大的点，并在其附近加密网格重复上述过程直至网格间距小于控制误差为止[11]．

具体步骤为：

Step2 估计设计变量的上限值和下限值；

Step4 在各网点上逐一求出其目标函数值，检验是否在可行域中，对可行点计算其目标函数值，比较选出最大值；

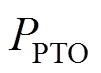
4 结语

本文对于波浪能装置垂荡和纵摇运动的最大输出功率做了较为完整的研究，并且系统分析了阻尼系数在一定范围内对能量输出系统带来的影响．利用模拟退火算法、网格搜索法、联合运动方程分析法等方法求得最大平均功率下对应的直线与旋转阻尼系数，计算便捷，结果可靠，并通过数值分析法减小误差，提高了模型求解精度．给出了浮子与振子在不同时间的运动方程及角度参量，具有较高的模型整合度，便于模型推广．

本文中建立了浮子与振子的运动模型（垂荡和纵摇运动），并提供了相应的求解方法，为其他形式的波浪能装置（如浮力摆式）、半浅式平台及船舶迎浪的垂荡、纵摇运动研究提供了模型基础，对于实际的波浪能装置中能量输出系统的选择也有一定的借鉴意义．

[1] 丁松，韩端锋．垂荡式波浪能装置运动模型数值分析[J]．海洋工程，2016（4）：107-117．

[2] 中国工业与应用数学学会．2022年高教社杯全国大学生数学建模竞赛赛题[EB/OL]．（2022-09-15）[2022-11-15]．http://ahdmcm.ahu.edu.cn/2022/1115/c20669a297066/page.htm．

[3] 张万超．轴对称垂荡浮子式波能装置水动力及能量转换解析研究[D]．哈尔滨：哈尔滨工程大学，2017．

[4] 张亮，国威．双自由度浮体的CFD模拟与能量吸收特性分析[J]．哈尔滨工业大学学报，2016，48（1）：126-132．

[5] 赵晓春．浮力摆式波浪能发电装置功率优化研究[D]．天津：天津理工大学，2020．

[6] 屈承珺，纪昌明，张验科，等．基于模拟退火的改进分布估计算法研究[J]．计算机应用研究，2020，37（增刊1）：138-139．

[7] 杨真真，方秀男．模拟退火算法及实例应用[J]．中国科技信息，2021（15）：65-66．

[8] 陈志．锚泊浮台波浪能供电装置液压系统研制与功率特性研究[D]．济南：山东大学，2020．

[9] 陈启卷，许志翔，岳旭辉，等．波力发电液压PTO系统蓄能器特性建模与参数优化[J]．应用基础与工程科学学报，2019，27（1）：226-237．

[10] 牛宏伟，池波．一种波浪能转换装置及其液压式PTO变阻尼控制策略研究[J]．船电技术，2018，38（9）：57-60．

[11] 施皓晨，肖海鹏，周建江．一种双线性分段二分网格搜索SVM最优参数方法[J]．计算机与数字工程，2020，48（9）：2179-2184．

Maximum output power designof wave energy based on heave and pitch motion models

LI Yongda，WANG Hengkai，LI Penghui，CHEN Hao

（School of Mathematical Sciences，Huaibei Normal University，Huaibei 235099，China）

The design of maximum output power of wave energy device is studied．Based on the theoretical background of motion balance equation and energy output system research，the heave and pitch motion model and the optimal damping coefficient model of float and vibrator are established．The heave displacement and velocity and pitch displacement and angular velocity of the float and vibrator at a given time are determined．The maximum output power and the optimal damping coefficient under the given parameter values are determined by simulated annealing algorithm and grid search algorithm respectively for two situation．

wave energy；maximum output power；heave and pitch motion model；simulated annealing algorithm；grid search algorithm

O29

A

10.3969/j.issn.1007-9831.2024.02.005

1007-9831（2024）02-0020-07

2023-03-01

安徽省高等学校质量工程项目（2020jyxm1670，2021jxtd257）

李勇达（2002-），男，安徽淮北人，在读本科生．E-mail：3033504738@qq.com

陈昊（1982-），男，安徽濉溪人，副教授，博士，从事数学建模、动力系统理论及应用研究．E-mail：chh0308@126.com