SpMV计算的ARM和FPGA异构加速器设计*
2024-02-28朱明达薛济擎艾纯瑶
朱明达,薛济擎,艾纯瑶
(中国石油大学(北京) 信息科学与工程学院,北京 102249)
0 引 言
随着人工智能技术的快速发展,算力向前端及边缘端迁移的趋势愈加明显[1]。由于功耗、体积方面的限制,ARM(Advanced RISC Machine)、FPGA(Field Programmable Gate Array)成为了边缘端算力实现的重要载体。稀疏矩阵向量乘(Sparse Matrix-Vector Multiplication,SpMV)常用于低延迟和高吞吐量的数据分析工作,除了在许多科学计算应用中占据主导地位,在边缘数据分析处理中也越发重要。然而,SpMV的性能受到可用存储带宽的限制,ARM的串行计算特点只能维持峰值计算性能的一小部分,这使得SpMV在边缘端有效实现极具挑战性。
近年来,许多学者开展了对SpMV运算加速的研究。文献[2]提出了一种基于高带宽内存的数据流SpMV加速器,克服了大矩阵存储的问题;还提出了两步流处理方法,但导致了FPGA资源开销非常高。文献[3-4]提出的FPGA加速方法通用性相对不足。文献[5-8]提出的方法基于CPU或GPU来实现[9-11],功耗较高,不利于在边缘端实现。在实现平台上,对比CPU及GPU,FPGA可以为不容易并行化的结构提供位级并行计算[12],具有高并行性、强控制能力和可重构性,逐渐成为加速计算的重要解决方案,是边缘端ARM方案的重要补充。
本文基于异构Zynq系列FPGA设计了一种多端口、高吞吐量的SpMV存储格式与加速系统:①设计了多端口改进的行压缩存储格式(Modified Compressed Sparse Row Format,MCSR)存储稀疏矩阵,提高并行度与计算效率;②研究了在嵌入式异构平台上加速算法的实现,在FPGA上完成对算法的加速,使用ARM完成对系统的控制,在ARM+FPGA的架构上利用软硬件协同方式对加速方法进行了验证;③ARM+FPGA并行加速后的设计相比于单ARM方案可以达到10倍的加速效果,计算效率显著提升,特别是矩阵规模越大非零值越多加速效果越明显。
1 加速方法
1.1 稀疏矩阵的存储格式
为了减少稀疏矩阵的存储空间,避免零值参与产生无意义的计算,一般采用特定的存储格式,常用的有三元组存储格式(Coordinate Format,COO)和行压缩存储格式(Compressed Sparse Row Format,CSR)[13-14]。目前稀疏矩阵较常用、效率也较高的存储格式是CSR格式,但作为一种针对矩阵的通用方法,CSR格式在基于FPGA实现时并不是最高效的。由于CSR格式中row_ptr行偏移数组存储的是行起始偏移位置,每行非零元素个数需要在迭代过程中才能确定,因此外循环不能使用循环流水优化方法,必须按顺序执行。这使得SpMV计算效率低下,迭代延迟很高。为了解决这个问题,本文使用MCSR存储格式,并在此基础上进行改进。
如图1(a)所示,MCSR格式中的col_index、value数组与CSR格式相同,不同之处在于它将CSR格式的row_ptr行偏移数组更改为row_len行长度数组,即存储每行非零元素的个数。结合FPGA的特点,为了使用多端口计算进行硬件优化,本文先将MCSR格式行、列索引合并起来,形成新的indices索引数组,再将indices和value数组按行分成p部分。合并后的单端口MCSR格式如图1(b)所示,通过连接row_ptr和对应数量的col_index来定义。行、列索引的交错合并过程不包括任何计算,可在边缘计算平台上处理,也可在本地预处理。在此基础上,将单端口MCSR格式进一步优化为多端口MCSR格式,以便利用多个端口并行存取数据来提高算法性能。通过将输入的稀疏矩阵按行分成p部分,每一部分单独处理,来实现p倍的运行加速。图1(c)展示了当p为2时indices和value数组的分块结果。具体分块的p取值将在多端口计算方法中详细阐述。

图1 MCSR存储格式
1.2 硬件优化方法
针对SpMV的运算特点,本文将硬件优化方法分为两类:任务级优化和数据级优化。任务级优化包括多端口计算、数据流、循环流水。在使用优化的多端口MCSR存储格式时,可使用数据流实现多端口任务并行,使用循环流水实现每个端口内的任务并行。数据级优化包括数组分割和流传输。数组分割实现了数据读写的并行,流传输实现了数据的缓存。
1.2.1 多端口计算
SpMV计算包含读、计算和写3个任务,为了提高读、写任务的数据吞吐量,本文利用多个端口并行地将数据从存储器传输到FPGA。如果FPGA包含D个存储器端口,每个端口具有B位,稀疏矩阵value、indices中的每个元素分别为g、h比特,可将输入稀疏矩阵的行分成p部分对应多端口MCSR的p个端口,每一部分都单独处理,从而最大限度提高p倍运行速度。p计算公式如式(1)所示:
(1)
每个硬件线程计算输出向量y的一部分,最后将y合并保存到BRAM中并传输到DDR中。增大p值可有效减小SpMV计算延时,但会增大资源利用率。综合考虑延时与硬件资源后,本文选择端口数p=8进行实验。
1.2.2 数据流
数据流优化方法实现任务级流水线,允许函数或循环之间的操作并行执行,可减少时延,增加RTL并发度,提高总体吞吐量。不使用数据流优化时,所有操作默认顺序执行。例如,程序必须在访问数组的函数或循环之前完成对数组的所有读、写访问。这严重限制了下一个使用数组的函数或循环的启动操作。使用数据流优化后,当前函数或循环中的操作可在上一个函数或循环完成其所有操作之前启动,如图2所示。
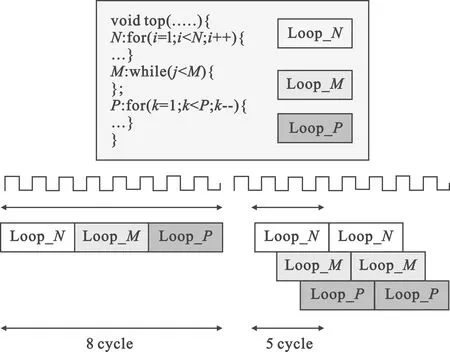
图2 数据流优化方法
如图3所示,顺序函数之间具有数据流,在循环之间插入Channel通道(Ping-pong RAM、FIFO或Register),以确保数据可从一个循环异步流到下一个循环。

图3 数据流优化方法细节
在使用优化的多端口MCSR存储格式计算SpMV时,每个端口之间数据不存在相互关联,因此可使用数据流实现多端口任务并行。其中可并行的任务如下:多个端口indices和values数据的并行读入、缓存;多个端口indices数据中rows和cols的并行缓存;多个端口待计算值(稀疏矩阵中某一元素)与列向量对应位的累加求和;多个端口的results数据的并行缓存、输出。具体数据缓存类型的选择将在后文流传输方法中阐述。
1.2.3 循环流水
针对单个循环的优化,一般采用循环流水,例如在for循环中对循环下的代码做流水化处理。当输入的数据不存在依赖性时,可并行化对数据进行读、计算和写操作,此时可将任务间隔优化到1,相当于一个时钟周期一个运算单元可完成一个操作。循环流水方法允许以并行方式实现循环操作,如图4所示。
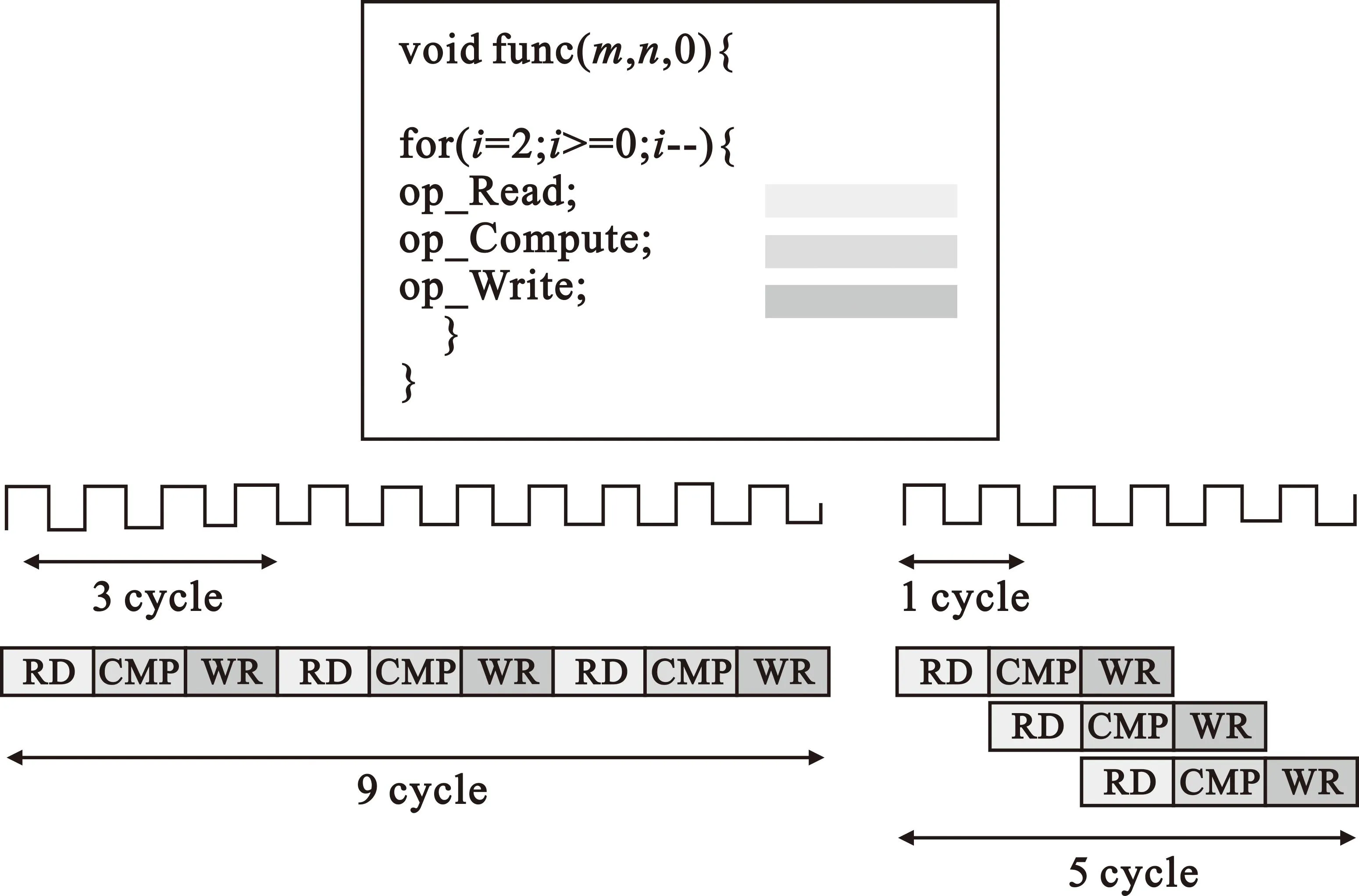
图4 循环流水优化方法
SpMV运算中数据是顺序流动的,每个端口内数据不存在相互关联,因此可使用循环流水实现每个端口内的任务并行。其中可并行的任务如下:每个端口indices和values数据的并行读入、缓存;每个端口indices数据中rows和cols的并行缓存;每个端口待计算值(稀疏矩阵中某一元素)与列向量对应位乘积的累加求和;每个端口的results数据的并行缓存、输出。
1.2.4 数组分割
在FPGA中,每个BRAM都有两个共享数据的可配置独立端口,用于片上数据缓存、FIFO缓冲。默认情况下数组中N个元素连续存储在一块BRAM中,则一个时钟周期只能提供一个数据。为了最优化数据级流水线间隔,使用数组分割方法将原始数组(单一BRAM)拆分为多个更小的数组(多个BRAM)。这可有效增加内存的读写端口数量,改善设计吞吐量,提高数据读写并行度。
在每个端口待计算值(稀疏矩阵中的某一非零值)与列向量对应位乘积的任务中,默认情况一个端口中的indices与value数组分别连续存储在两块BRAM中。BRAM最大的端口数量为2,严重限制了读和写的吞吐量。因此为了改善带宽,使用数组分割方法将原一维数组按独立元素进行拆分,将内存分解为单个寄存器,有效实现了数据读写的并行。
1.2.5 流传输
流传输优化方法决定了数据流通道中的数据缓存类型。如图3所示,在数据流的函数主体或循环主体独立通道,将每项任务的结果缓存在通道中。根据不同任务可选择不同的数据缓存类型,如Ping-Pong RAM或FIFO。通常情况下,Ping-Pong RAM用来存取矢量数组,FIFO用来存取标量。数据流所添加的每个通道都包含用于指示Ping-Pong RAM或FIFO已满或已空的信号。流传输优化方法如图5所示。流传输方法的优势在于不需要地址管理,不足是读取完当前数据之后无法再次对该数据进行读取。但是由于SpMV运算只涉及数据的顺序读写,不受该不足影响,因此可使用流传输方法将数据流通道中的数据缓存类型配置为FIFO,可有效减小资源利用率,提高数据存取并行度。

图5 流传输优化方法细节
2 硬件实现
本文采用Xilinx ZCU102开发平台,基于Xilinx Zynq UltraScale+ XCZU9EG-2FFVB1156E MPSoC 芯片进行了实现与测试[15]。
基于ZCU102平台的加速结构如图6所示。AXI Interconnect为AXI总线实现PS端与PL端互联,Data Mover为数据搬运器,SpMV accelerator为稀疏矩阵乘法加速器。SD卡存入Linux系统硬件启动文件与数据,程序初始化时PS端将SD卡数据读入DDR4,PL端SpMV加速模块通过直接内存存取方式(Direct Memory Access,DMA)获取DDR4中的数据,PL端实现SpMV并行计算。

图6 基于ARM+FPGA的SpMV算法加速结构
本文采用Xilinx的SDSoC开发环境,将.cpp文件分别转换为BOOT.bin、image.ub、.elf文件和.bit文件。其中,BOOT.bin为启动文件,包含引导加载程序(FSBL)、引导程序(U-Boot);image.ub包含Linux启动映像;.elf为应用程序的二进制可执行文件,可在Linux系统中调用相关软硬件资源,完成数据的读取、输出和运算;.bit为FPGA比特流文件。图6给出了基于ARM+FGGA的SpMV算法加速结构。
在硬件设计中,数据传输接口的设计尤为重要。本文中,由于传输稀疏矩阵非零值与计算结果时涉及较大数据量,因此选用AXI MM作为Data Mover传输数据,使用SDS data mem attribute指令约束数据存储地址连续性。相比AXI GP与AXI ACP,AXI HP接口有更高的读写带宽,且AXI MM Data Mover 要求PL端口为主端口,PS端口为从端口,因此选用AXI HP接口,使用SDS data zero_copy指令约束数据传输量。由于Random接口实现数据随机读取会占用较多的BRAM等片上资源,且SpMV计算过程中数据是顺序读取或写入的,因此选用Sequential接口,使用SDS data access pattern指令约束硬件函数数据访问方式。
根据本文提出的加速优化方法对SpMV进行硬件优化,结合以上加速结构,可得到优化后的SpMV程序分析结果,如图7所示,可以看出程序已经实现了多端口indices、values数据的并行读入、缓存,和多端口results数据的缓存、输出。图中,fmul为程序中的乘积操作,fadd为乘积结果与缓存results值的累加求和操作,已经实现了乘积与累加求和的并行操作。
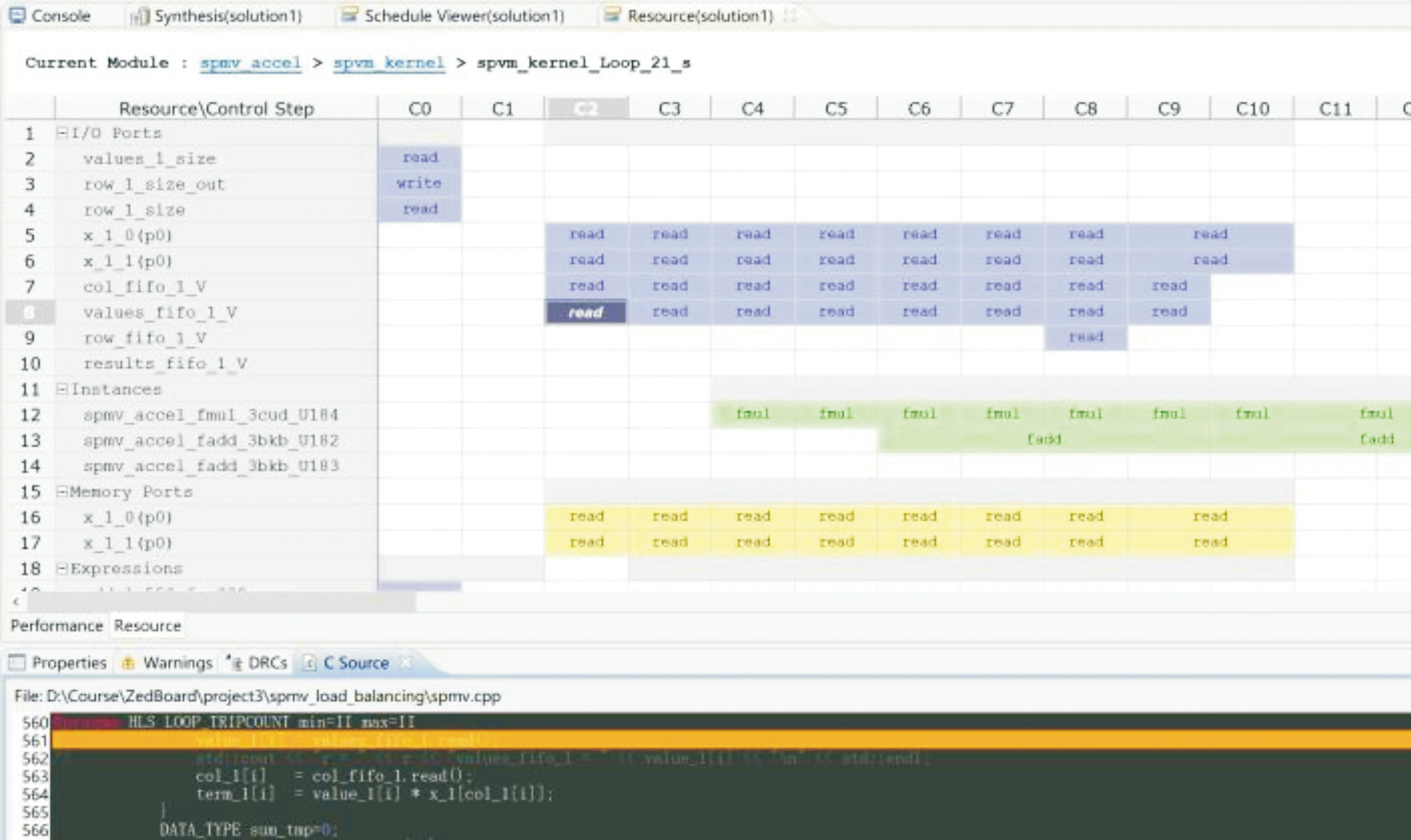
图7 SpMV 程序分析
3 结果分析
3.1 数据集介绍
佛罗里达大学(University of Florida)稀疏矩阵库包含大量从应用程序中收集的稀疏矩阵,被广泛应用于基准测试。本文从中选择19个不同类型的稀疏矩阵,行列数范围在102~105,非零值数量在102~106。在计算SpMV时,稀疏矩阵是所选测试矩阵,密集向量是rand()函数产生的随机数。rand()%(b-a+1)+a可以产生[a,b]范围的一个随机整数,本文选取a=0,b=1做测试。稀疏矩阵的属性包含行数m、列数n、非零值、稀疏度、2D图、3D图,如表1所示。
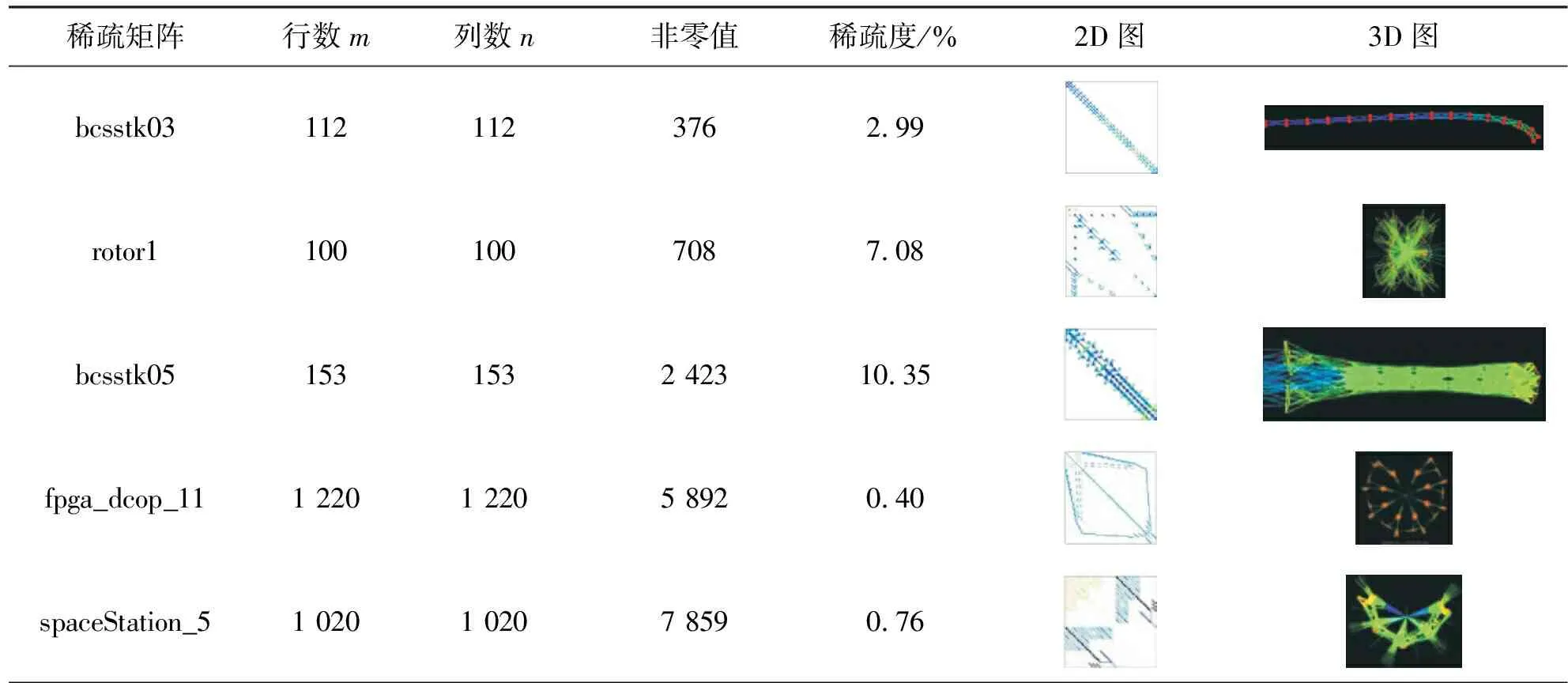
表1 稀疏矩阵属性
3.2 性能对比
为了验证系统性能,本文分别完成了基于PS端(即ARM)和基于PS+PL(即ARM+FPGA)的系统设计。基于PS的设计是只使用ARM处理器系统完成全部计算,而基于PS+PL的设计将SpMV移植到PL端完成,由FPGA实现SpMV计算加速。
在ARM+FPGA系统设计中,又分别实现了SpMV并行加速前与并行加速后两种设计。SpMV并行加速前采用原始的CSR存储格式,并行加速后采用本文的多端口MCSR格式+数据流+循环流水+数组分割+流传输的硬件优化方法。这一对比中变量为加速方法,不变量为测试的稀疏矩阵和FPGA实现平台。通过对比并行加速前后SpMV的硬件资源利用率、处理所需时间等性能指标,评价SpMV的硬件优化效果。
因此,本文一共实现了3种系统设计方式进行对比,分别是“单ARM”方案、“ARM+FPGA并行加速前”方案、“ARM+FPGA并行加速后”方案。分别对所选的19个稀疏矩阵进行SpMV计算对比,运行时间如图8所示,“ARM+FPGA并行加速后”相对于“单ARM”的加速比如表2所示。可见当稀疏矩阵规模较小非零值较少时“单ARM”的计算效率较高,但是当规模变大非零值少量增加就会导致ARM计算效率下降。而随着矩阵规模增大非零值增加,本文提出的“ARM+FPGA并行加速后”方案加速效果显著提高。

表2 SpMV计算核心横向对比结果
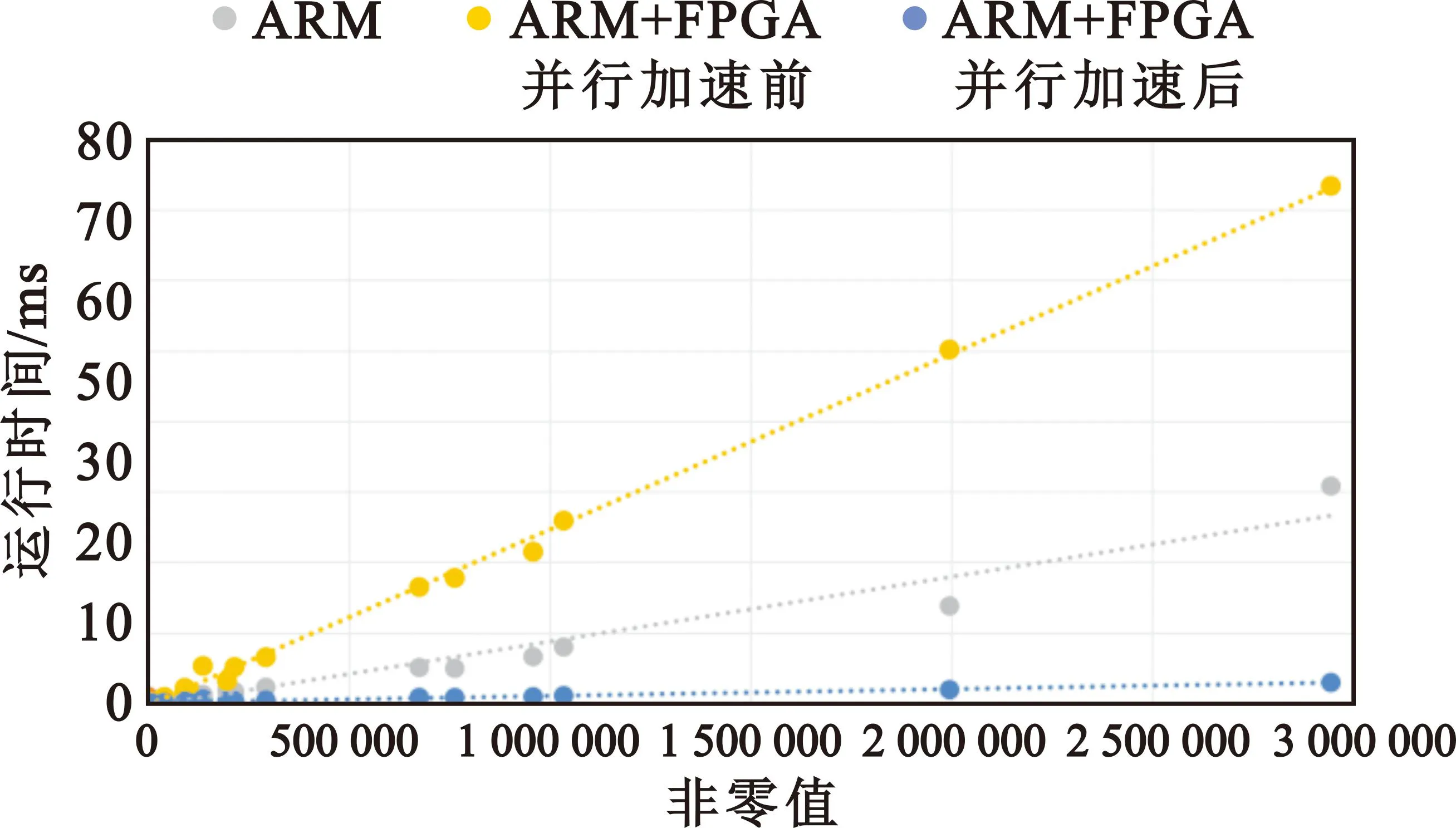
图8 SpMV 计算运行时间
根据FPGA开发软件Vivado生成的资源使用报表可以看出,优化前后FPGA的核心资源利用率有所增加,增加的资源消耗在可接受范围内,如表3所示。优化后实现了并行加速,各硬件资源利用率相比优化前略有增加。
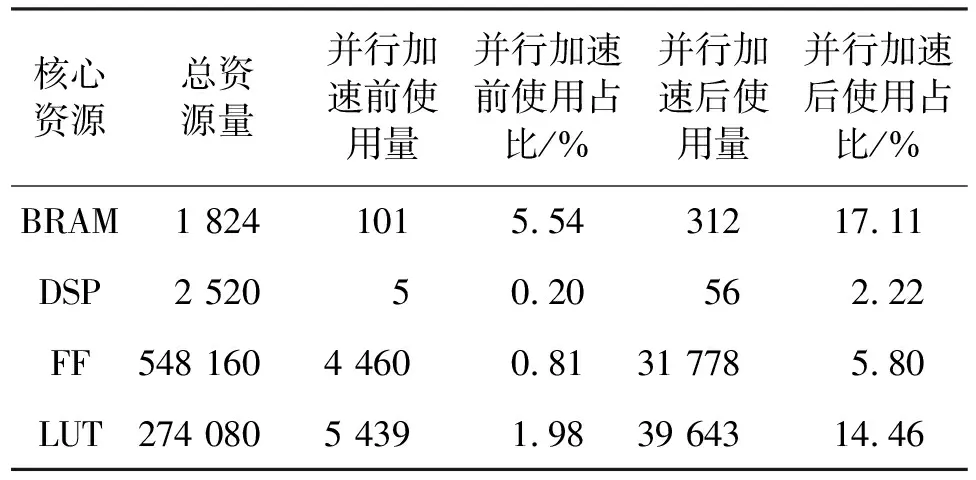
表3 并行加速前后FPGA核心资源使用对比
4 结束语
本文针对FPGA的SpMV计算加速问题提出了一种多端口的MCSR存储格式,结合数据流、循环流水、数组分割、流传输等加速优化方法实现了SpMV加速求解器设计。对比研究了“单ARM”“ARM+FPGA并行加速前”“ARM+FPGA并行加速后”3种SpMV的计算耗时与资源使用,实验结果表明,本文设计的加速器在稀疏矩阵规模增大非零值越多的情况下加速效果越明显。在本文所实验的稀疏矩阵中“ARM+FPGA并行加速后”相较于“单ARM”方案最高可以达到10倍的加速效果,而且增加的资源消耗在可接受范围内。因此,本文方法在边缘端实施SpMV计算方面具有一定的优势。
本文为了保证3种对比方案数据的一致性,都使用了浮点数计算,虽保证了计算准确率,但增加了FPGA硬件资源消耗。后续工作计划采用浮点数转定点数的方法,争取用有限的准确率损失换取硬件资源利用率的减少。
