基于辛Runge-Kutta方法的棋盘形褶皱二维薄膜-基底结构动力学特性研究

张博涵, 曹善成, 王 博,4, 欧阳华江, 徐方暖

(1.西北工业大学 工程力学系,西安 710072;2.西北工业大学 航天学院,西安 710072;3.西南交通大学 机械工程学院, 成都 610031;4.大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室,大连 116024)

1 引 言

基于力学屈曲原理[1]的无机可延展电子器件,既能保持无机功能电子器件优异的电学性能[2,3],还能使硬而脆的无机电子器件具备拉伸、压缩、弯曲和扭曲等延展性能;因此,该类电子器件受到了学术界和工程领域专家学者们的广泛关注。基于力学屈曲原理的薄膜-基底结构,是将刚性硬而脆的薄膜型功能电子器件层粘合在预拉伸的柔性基底上;然后,释放掉柔性基底上的预拉伸应变后,薄膜中产生压缩的残余应变,致使薄膜结构在柔性基底上表面处发生褶皱变形[4]。

针对薄膜-基底结构的力学屈曲褶皱,已有大量的理论研究、实验及有限元工作开展[5-9]。其中,实验研究结果表明,当薄膜结构受到压缩应变时,薄膜会在柔性基底表面形成一维波纹(1D wavy)、人字形波纹(herringbone wavy)和棋盘形波纹(checkerboard wavy)等三种类别的褶皱[10]。针对该类结构的失稳特性,文献[11,12]从静力学设计角度,研究了该类薄膜-基底结构失稳机理特性。然而,这类电子器件在应用过程中,不可避免会需要承受或者工作于复杂动态的环境中[13-15];准确评估该类结构动态力学行为是其从理论设计走向实际应用需要解决的问题之一。

针对存在一维波纹薄膜结构的动态力学行为,目前国内学者也开始关注。Ou等[16,17]研究了一维薄膜-基底结构的动力学行为,并通过雅可比椭圆函数,解析地给出了该结构的动态振幅表达式。Ma等[18]研究了基底为有限厚度时的非线性自由振动。Wang等[19]分析了表面效应和压电效应对弯曲薄膜结构动态行为的影响,以避免复杂环境中的共振。Bi等[20,21]研究了具有中间层的薄膜-基底结构的动态行为,得到了含中间层时的解析非线性频率,并分析了中间层对结构动态行为的影响。然而,针对薄膜结构的二维褶皱,即当该薄膜-基底结构发生人字形或棋盘形褶皱模式时,这类结构的动态力学行为鲜有研究。因此,本文将研究棋盘形褶皱薄膜-基底结构的动力学行为特性。

2 硬薄膜-柔性基底能量计算

2.1 模型描述

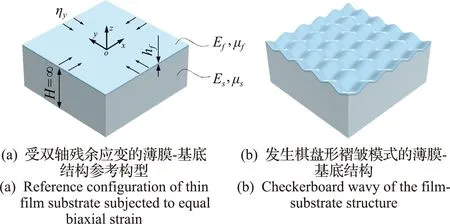
图1 薄膜-基底结构与棋盘形褶皱

在理论分析中,薄膜建模为冯·卡门理论描述的薄弹性板,认为基底是半无限线弹性体。图1(a)所示的参考构型中定义了计算所用的坐标系,坐标原点O位于薄膜的中性层;平面内的x轴和y轴分别指向双轴载荷的主应变方向;z方向代表薄膜的厚度方向。本文采用能量方法,建立二维薄膜-基底结构的振动控制方程;因此,需要分别计算出二维薄膜-基底结构的动能和势能。

2.2 薄板结构势能

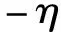
(1)

线弹性二维薄膜的本构关系为

(2)

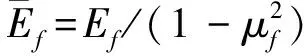
根据文献[9],薄膜结构会受到的横向牵引力T3及面内牵引力T1和T2分别为

(3)

(4)

(5)

根据文献[20-21]可知,二维薄膜结构的势能Uf包含两部分,一个是薄膜结构的弹性势能Uf,其由于薄膜结构受到弯曲变形产生;另外一个为膜能Ufs,其由于薄膜受到拉伸变形产生

Uf=Ufb+Ufs

(6)

式中Uf和Ufs的计算表达式为

(7)

(8)

式中S为积分区域的面积。

2.3 柔性基底弹性应变能

基底建模为薄膜以下的半无限空间,假设基底失稳时表面出现了w(x,y)的位移,以w(x,y)作为边界条件代入半无限大空间的弹性响应问题[11]中可求得基底的能量表达式。对于薄膜-基底结构的二维褶皱问题,根据文献[12]可知,该结构中的弹性应变能计算为

(9)

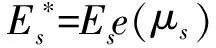
为褶皱位移w(x,y)的傅里叶变换形式,其变换表达式为

(10)

3 棋盘形褶皱结构振动控制方程

如图1(b)所示的棋盘形褶皱结构的面外位移w(x,y,t)可以假设为[12]

w(x,y,t)=A(t)cos(k1x1)cos(k2x2)

(11)

式中 待定参数A(t)为随时间变化的褶皱幅值,k1和k2为褶皱波纹沿x方向和y方向的特征波数。在计算二维薄膜-基底结构的势能时,本文还需要计算二维薄膜的面内位移u和v。文献[9]指出可忽略薄膜/基底界面处的面内牵引力对褶皱波长和振幅的影响。在分析二维薄膜-基底结构屈曲失稳时,假设T1=T2=0,这样,根据方程(1～4)可以求出面内位移u和v的表达式为

(12)

(13)

将方程(12～14)代入方程(7,8)可以得到薄膜结构的弯曲能和膜能分别为

(14)

(15)

把面外位移式(11)代入式(9),可以得到存储在柔性基底中的弹性势能为

(16)

二维薄膜的动能计算表达式为

(17)

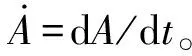
根据Lagrange方程,可以得到棋盘形褶皱薄膜-基底结构的振动控制方程,Lagrange方程表达式为

(18)

式中 Lagrange函数L的表达式为

(19)

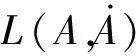
(20)

式中 系数α1和α2为

(21)

为了分析计算方便起见,引入无量纲参数

(22)

将式(22)的无量纲式代入方程(20),可以得到无量纲的振动控制方程为

(23)

(24)

4 数值方法

辛数值方法在求解保守系统问题时,展现出优异的保辛特性(如动量守恒和相体积守恒)[22,23]。针对非线性振动控制方程(23),其解析解很难得到,因此本文采用数值计算精度高和稳定性好的辛Runge-Kutta法对其进行数值求解。

在进行数值求解前,本文需要将二阶动力学方程进行降阶处理,即需要引入新的变量

(25)

然后,利用方程(25),方程(23)可以改写为如下一阶微分方程组

(26)

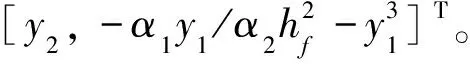
本文采用二级四阶的辛Runge-Kutta方法,其迭代格式为[24]

(27)

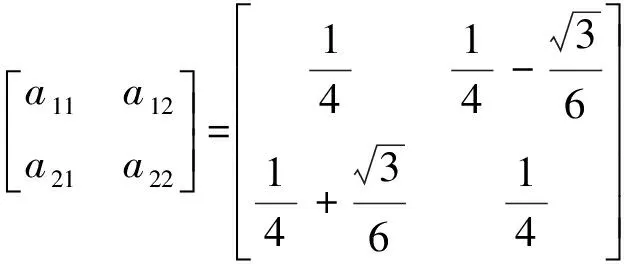
(28)

5 结果与讨论

5.1 数值算例

表1 薄膜和基底结构的材料和几何参数[12]

薄膜-基底结构的Hamilton能量可以写为

(29)

图2 Hamilton能量误差

为了进一步展示辛数值方法的数值稳定性,图3和图4分别对比了两种不同步长下的薄膜-基底结构的时间位移曲线。

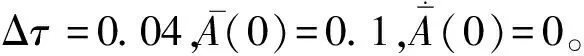
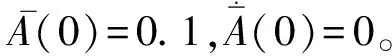
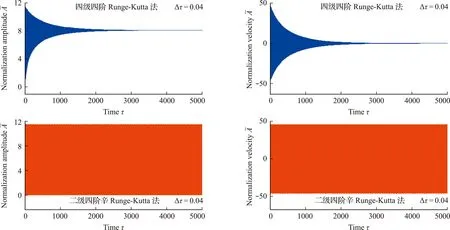
图3 二级四阶辛Runge-Kutta法和经典四级四阶Runge-Kutta法在步长Δτ=0.04时的仿真结果

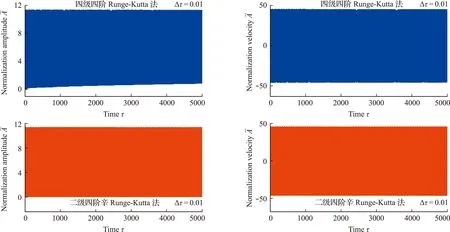
图4 二级四阶辛Runge-Kutta法和经典四级四阶Runge-Kutta法在步长Δτ=0.01时的仿真结果

对方程(26)描述的保守系统,其另一个性质是相空间中的轨线围成的面积不随时间演化而变化。图5绘制了薄膜-基底结构的相位。可以看出,在不同时刻下,采用辛数值方法得到的相位曲线始终为一条曲线;不会发生数值耗散现象。即验证了辛数值方法在保守系统下的保结构特性[15]。

图5 步长精度Δτ=0.01,Δτ=0.02时随时间演化的相位

5.2 静态分岔

在方程(26)中,令f(τ,Y)为零,可以解析得到薄膜-基底结构静态振幅表达式和临界预应变的表达式为

(30)

(31)

(32)

图6 薄膜-基底结构失稳的分岔

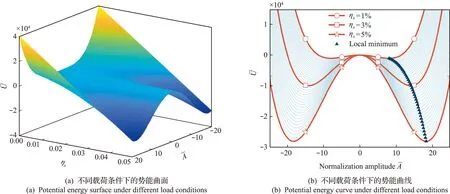
图7 棋盘形波纹的势能与预应变载荷x和波纹幅值的关系

6 结 论

本文研究了二维棋盘形褶皱薄膜-基底结构动力学行为。首先将二维薄膜结构等效为薄板结构,将柔性基底等效为半无限大基底结构,计算了薄膜-基底结构系统总能量;通过拉格朗日运动方程得到了该棋盘形褶皱的振动控制方程。然后,应用二级四阶辛Runge-Kutta法求解该方程,通过数值试验,验证了辛数值算法的有效性和优越性。主要结论如下。

(1) 数值试验验证了辛算法具有保结构、保能量的特点。辛Runge-Kutta算法能够很好地保持棋盘形褶皱薄膜-基底结构原有的能量守恒特点,能够保证该结构在振动过程中长时间数值稳定。

(2) 棋盘形褶皱薄膜结构的振动会围绕在其静态幅值附近。通过调控预应变可调控棋盘褶皱的静态幅值,随着预应变的增加,静态幅值递增。