超大型航天结构动力学与控制的保辛方法
2024-02-27邓子辰李庆军安思奇李纪辉
邓子辰, 张 凯, 李庆军, 安思奇, 李纪辉
(1.西北工业大学 工程力学系,西安 710072;2.西北工业大学 航空学院,西安 710072;3.中山大学 航空航天学院,深圳 518107;4.西湖大学 工学院,杭州 310024)
1 引 言
超大型航天器是未来重要的空间基础设施,是各航天大国未来竞争的重要领域[1]。如可提供吉瓦量级电能的空间太阳能电站[2]或将太阳光反射至地面的超大型太空反射镜[3],将是缓解能源危机、实现双碳目标的航天方案;超大尺寸卫星天线和超大口径空间望远镜将极大拓展人类观测地面目标和宇宙深空的能力[4]。
自从美国Glaser博士提出空间太阳能电站的概念以来,美国能源部和NASA高度重视其发展,提出了第一个系统性的空间太阳能电站设计方案,开展了大量的经济和技术可行性论证工作[5]。近年来,美国还开展了多次太阳能发电和无线能量传输的在轨验证研究[6]。与此同时,日本也开展了多次无线能量传输技术试验,提出了编队飞行方案、绳系方案等多种空间太阳能电站概念设计方案[7]。中国也提出了空间太阳能电站发展的三步走战略,并成立了中国宇航学会空间太阳能电站专业委员会,提出了多旋转关节空间太阳能电站和SSPS-OMEGA等代表性概念设计方案[8-10]。
超大型航天器动力学的建模、计算和分析是制约上述结构制造和服役的关键问题[11]。目前,学术界针对常规尺寸航天器的动力学与控制已有相对充分的研究[12,13]。然而,超大型航天器在结构方面具有超大尺寸(百米~千米量级)和超大质量(百吨量级至万吨量级)的特点,在复杂空间干扰力的作用下表现出独特的动力学行为[14],现有的分析计算方法难以准确得到相应结构的动力学行为。主要体现在,(1) 在空间环境干扰力和控制力的作用下产生大幅结构变形,而结构变形进一步通过惯性分布力、空间环境干扰力和控制力/力矩等影响轨道和姿态运动,引起轨道-姿态-结构耦合问题[15]。(2) 由于结构构型巨大,结构振动将以弹性波的方式在结构中传播,使超大型结构表现出超低频振动与波动共存的问题[16]。(3) 受限于火箭运载能力和包络限制,需要发展高收纳比的空间可展开结构和功能可调的新型结构(或材料),以满足超大型航天结构的功能需求[17]。
超大型航天器的动力学模型具有高维、非线性和包含约束等特点[16],并且航天动力学系统通常具有多种物理量守恒的性质(如能量守恒、角动量守恒和约束守恒等),因此在数值计算中保证计算效率、精度和稳定性的同时,如何尽可能多地保持原系统的固有性质,是实现此类结构动力学行为准确计算的关键[14]。自冯康院士提出Hamilton系统辛算法以来,保辛算法在保持Hamilton系统辛几何结构、保持系统总能量守恒、保持约束守恒等方面的优势得到了普遍的认可[18]。钟万勰院士将辛算法引入到计算力学领域,提出了空间维度的保辛概念,建立起了以传递辛矩阵群为基础的一套完整经典力学保辛理论体系,将分析力学发展到分析结构力学新层次[19-21],并针对一类多体动力学问题导出的微分-代数方程,提出了可以同时保辛和保约束的祖冲之类算法[22,23]。正是由于这些优势,保辛算法为解决超大型航天器复杂的动力学与控制问题提供了有效途径[24-26]。
综上所述,针对超大型航天器的发展,亟需建立其动力学模型,针对轨道-姿态-结构耦合行为,构建相应的高效和高精度数值求解算法,发展相应的控制方法,并探索结构低频振动和波动行为调控的方法,为超大型航天器设计与应用提供理论支撑。近年来,西北工业大学邓子辰教授团队和中山大学吴志刚教授团队基于保辛算法的学术思想,提出了非线性约束Hamilton系统的保辛计算方法和波传播辛分析方法,在此基础上开展了空间太阳能电站长时间在轨运行的轨道-姿态-结构耦合动力学建模、动力学特性分析与控制方法研究,并开展了面向超大型航天器结构动力学分析与设计方法研究。
2 超大型航天结构的多体约束系统和结构振动的保辛算法
2.1 多体约束动力学系统的保辛算法
常规尺寸航天结构的动力学研究通常不考虑轨道-姿态-结构耦合的动力学行为。对于超大型航天结构,结构变形将通过空间环境干扰力和控制力对系统的轨道和姿态产生影响,引起特殊的轨道-姿态-结构耦合效应。基于自然坐标法和绝对节点坐标法,超大型航天结构的轨道-姿态-结构耦合动力学模型可表示为
(1)
式中q为系统的广义坐标,p为广义动量,M为质量矩阵,g(q)为系统的约束,λ为Lagrange乘子,Ug(q)为系统的万有引力势能。为了阐述动力学方程的数值求解算法,将式(1)简写为以下微分代数方程形式
(2)
式中x=[qT,pT]T。
为了对式(2)进行数值求解,一般需要将约束方程对时间求导
(3)
通过式(2,3)的微分方程联立,将式(2)转化为一组常微分方程组,并采用常规的常微分方程数值算法进行动力学求解[27]。然而,这种做法会带来约束违约的问题,即式(2,3)的约束方程并不完全等价,在数值求解过程中约束方程无法得到满足,进而引起系统的快速发散。为此,Wei等[28]提出了在约束Hamilton系统中引入位移级投影、速度级投影、加速度级投影以及能量守恒投影,数值结果表明,通过投影算法保证了系统的约束和能量守恒,达到了较好效果。
以上述方法为基础,针对航天器姿态动力学单位四元数仿真中的守恒量违约问题,徐方暖等[29]提出了显式投影方法。根据单位四元数的定义,存在以下守恒量
(4)
采用投影算法将动力学求解结果向方程(4)进行投影,即
(5)
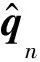
(6)
通过式(6),即可得到刚体运动学单位四元数的显式投影方法。然而,对于约束方程维数较高和形式复杂等情形,难以获得投影算法的显式解析解。
上述方法属于缩并法,需要通过对约束方程求导并与微分方程联立,消去微分方程中的Lagrange乘子。微分代数方程的另一类求解算法是增广法,其求解过程不需要消去Lagrange乘子,而是将微分方程和代数方程一起离散并迭代求解。针对一般的约束Hamilton系统,钟万勰等[19,22]提出了祖冲之算法的思想,认为约束只需要在时间节点处满足即可,并提出了时间有限元方法和保能量-保约束方法,并且证明了保能量-保约束算法具有保辛性[23]。Li等[30]进一步提出了基于二级四阶辛Runge-Kutta方法的保能量-保约束方法,并将其应用于空间多刚体系统姿轨耦合动力学仿真,其离散格式为
(7)
式中τ为时间步长,且
(8)
该算法中,式(8)在每一步都需要迭代求解,且认为λn+1在该时间段内为常向量,这与祖冲之类算法中约束不必处处满足,只需在节点处满足的思想相对应。在多体动力学领域,学者们常采用具有可调耗散因子的数值算法,使柔性多体系统中的高频动力学响应得到耗散的同时保留低频响应,从而适当增加数值仿真步长[31]。然而,对于多体动力学模型,数值耗散将导致轨道运动能量耗散,这意味着轨道长半轴出现仿真误差。因此,在研究航天多体动力学系统时,采用式(7,8)的保能量-保约束算法,使数值仿真结果真实反映系统的几何约束特征。
2.2 周期结构的波传播特性的辛分析方法
超大型航天器的设计方案一般是由多个子结构在轨组装而成,因此形成的结构是典型的超大超柔周期性结构。由于结构构型巨大,结构的动响应将以弹性波的形式在结构中传播。因此,超大型结构表现出超低频振动与波动共存的现象,这也为周期结构波动行为分析和子结构设计提出了新的挑战。在传统周期性结构,尤其是杆系结构的波传播分析中,一般采用有限元方法得到结构的刚度K和质量矩阵M,并通过相应方法得到系统的特征值。但由于超大型结构尺寸巨大,建立的有限元模型巨大,带来了极高的分析计算成本。因此,需要发展新的波传播分析方法,以减少计算量并且提高计算精度。针对上述问题,以哈密顿系统的辛分析方法为基础,研究上述超大型周期结构的波传播问题。
通过获得单元的全局质量矩阵M和刚度矩阵K,周期结构的振动方程一般可表示为
[K(k1,k2)-ω2M(k1,k2)]U=0
(9)
式(9)中,可以通过给定波数(k1,k2)求解出对应的特征频率。根据上述分析,结构中弹性波频散关系的计算需要对周期结构进行网格划分。为提高计算的精确度,通常需将结构划分为多个子单元,但会导致计算过程中的质量/刚度矩阵维度过高,增加计算分析成本。因此,在研究中,通过利用一种保辛算法来解决这个问题。该方法已成功应用于求解一维结构的振动分析[32,33],克服了计算成本高的问题。
对于任意给定的特征频率ω#,动态刚度矩阵[34]可以表示为
R(ω#)=K(k1,k2)-ω2M(k1,k2)
(10)
将单元的位移分为内部位移(Ui)和外部位移(Ue),其中i和e分别为单元的内部和外部节点。式(9)可以重新写为
(11)
可以获得外部动态刚度矩阵
Re(ω#)=Ree(ω#)-Rei(ω#)[Rii(ω#)]-1Rie(ω#)
(12)
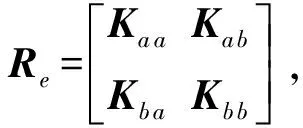
(13)
由布鲁赫定理可知,边界节点的位移存在以下关系
ub=Aua
(14)
式中A=[I3×3exp(jk1),I3×3exp(jk2)]。将式(14)代入式(13)可以得到完整的动力学方程为
Kaa+A-1Kba+KabA+A-1KbbA=0
(15)
通过给定波数(k1,k2),可通过区段精细积分方法[34]求解上述方程(15)。利用该方法可通过对特征值计数及边界条件的比较分析,得到给定波数对应的频率值ω,保证不失根,不重根。然而,从上述推导过程可以看出,保辛算法消除了单元内部节点的振动和位移,导致从方程(15)中求解得到的特征值并没有覆盖结构中原有的特征频率。为了得到所有的特征频率值,可以使用特征值计数法来解决这个问题,该方法可以表示为
J(ω#)=s{Rii(ω#)}+s{Kqq(ω#)}
(16)
式中s{…}表示矩阵中负号的个数,J(ω#)表示小于给定频率ω#的特征值个数。因此,可通过计算具有不同ω#的特征值计数来获得结构的特征频率。使用保辛方法可以精确、快速求解复杂结构的色散关系,并进一步获得不同频率下的色散面和相/群速度,从而全面分析整体结构的波动特性。
3 超大型航天结构在轨耦合动力学与姿态控制的保辛分析
3.1 轨道-姿态-结构耦合动力学的保辛分析
空间太阳能电站在分布式空间干扰力、集中式或分散式控制力/力矩和分布式惯性力等作用下,将会出现独特的轨道-姿态-结构耦合现象。基于轨道-姿态-结构耦合动力学模型及保辛求解算法,李庆军等[35]针对圆形轨道上保持对日指向的支撑结构,研究了轨道和姿态对结构变形与振动的影响。研究发现,万有引力梯度引起的准静态变形随着梁长度的5次方增长,当结构的最低固有频率降低到轨道角频率的4倍左右时,万有引力梯度可能会引起结构共振现象。针对具有多个太阳敏感器和电推力器的超大型结构,研究了结构振动对轨道和姿态的影响,发现结构振动会引起传感器和推力器的位置和方向的偏转,产生推力和力矩的误差,从而引起轨道-姿态-结构耦合问题[15]。
为实现空间太阳能电站保持姿态控制的同时尽量降低燃料消耗,李庆军等[36]基于辛算法深入研究了准对日定向姿态的动力学特性,选取柔性梁的质量为m=48000 kg,长度为l=600 m,给定初始轨道为地球静止轨道,建立轨道-姿态-结构振动耦合动力学方程,发现准对日定向姿态的姿态摆动时,结构将受到线性分布的横向惯性力,这种分布方式正好与万有引力一阶展开的分布大小相等、方向相反,所以采用准对日定向姿态的最大控制力矩仅为对日定向姿态最大控制力矩的0.67%,如图1(a)所示。太阳冻结轨道上的准对日定向姿态不仅可以极大节省控制燃料,还能大幅降低结构振动幅值[37]。在研究准对日定向姿态的过程中,俯仰姿态角的相图是否封闭是判断准对日定向姿态的标准,辛算法在保持相空间轨迹封闭性方面具有独特的优势,因此在寻找准对日定向姿态数值解的过程发挥着重要作用。基于上述研究成果,提出了自由漂浮空间太阳能电站概念设计方案[38],如图1(b)所示。该方案采用了地球同步拉普拉斯轨道平面的太阳冻结轨道和准对日定向姿态,通过保能量-保约束算法求解系统的姿轨耦合模型,发现在轨运行过程几乎不需要轨道和姿态控制,节省控制燃料约95%。
3.2 基于多体约束系统保辛计算的姿态控制设计
空间太阳能电站在轨运行过程中,微波发射天线需要保持对地指向姿态,同时太阳能电池阵列需要保持对日指向姿态。Wie等[39]研究发现,为了抵消Abacus空间太阳能电站对日指向的万有引力梯度力矩,需要采用100000个控制力矩陀螺(质量共25000 t)或者500个离子推进器(在30年内需要消耗2550 t控制燃料)进行姿态控制,控制代价远超出常规尺寸航天器。针对空间干扰力矩具有周期性的特点,李庆军等[40]提出了连续系统的切换迭代学习控制方法,通过以往周期的力矩预测当前周期需要的前馈控制力矩,使控制精度提高10倍的同时传感器噪声的影响下降10倍。进一步地,将这种控制方法拓展到柔性空间太阳能电站中,发现该控制方法还能有效抑制结构振动,降低了姿态-结构耦合程度[41]。在此基础上,基于模糊推理设计了控制增益自主调整策略,使控制精度满足要求的同时把控制频率降到最低,避免与结构出现耦合[42]。
4 超大型航天结构波动力学行为与控制及可展开结构设计
4.1 空间可展开折纸结构波传播问题的辛分析
受火箭运载能力和包络限制,大型航天结构需在发射之前收拢到极小体积,入轨之后展开并组装,形成整体结构。这要求大型航天结构进行模块化设计,并且子结构需具有高收纳比和稳定可靠展收的性质。近年来,折纸结构等新型空间可展开结构,在大型空间结构的子结构模块化设计中得到了高度关注。
Zhao等[43]以大型空间太阳能帆板和天线结构为背景,将图2(a)的三浦折纸中的山线和山谷线等效为空间梁结构,其单胞的几何结构如图2(b)所示。采用2.2节周期性结构的波传播辛分析方法,计算得到如图2(c,d)所示的折纸晶格超材料的能带结构。通过与有限元方法进行对比,也能发现两种不同方法计算的能带结构相互重叠,表明了保辛方法计算折纸晶格超材料的能带结构的准确性。

图2 三浦折纸晶格超材料
4.2 厚板折纸结构展开动力学分析及结构设计
厚板折纸结构是一类考虑面板厚度的折纸结构,这类结构具有构型复杂、非线性约束方程众多等特点,给动力学建模与精确求解带来较大难度。Li等[44]采用自然坐标法描述可展平厚板折纸的位形和铰链约束(图3(a)),建立了带约束的Hamilton动力学方程,并采用保能量-保约束算法求解微分代数方程,分析常见厚板折纸结构在扭簧驱动下的自由展开过程。如图3(b,c)所示,数值仿真结果与实验结果吻合一致。仿真过程中系统总能量守恒,而且约束条件严格满足。除了分析可展平厚板折纸结构的展开行为,李纪辉等[45]受剪纸技术启发,设计出一种容纳面板厚度的可折叠三维多面体结构,并将其应用于空间可折叠伸展臂的设计[46],实验结果验证了该结构具有单自由度、高收纳比和便于操控等优点。
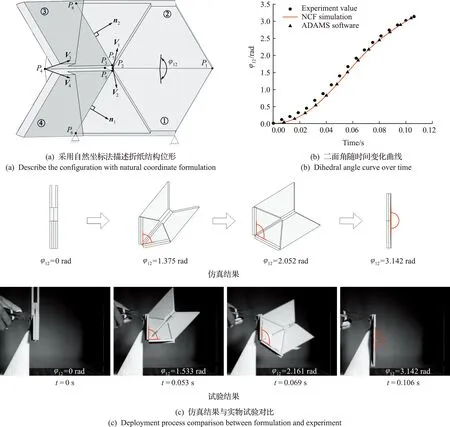
图3 厚板三浦折纸结构展开动力学建模与结果分析
4.3 三维手性空间可展开结构动力学与结构设计
具有手性特性的压扭耦合晶格超材料可以在低频范围内获得包含各种共振类型(弯曲、轴向和扭转)的带隙,并且不改变结构的质量和刚度[47]。Zhao等[48]针对构架式空间可展开结构设计了两种不同的手性单元,如图4(a,b)所示。通过分析手性晶格超材料的能带结构和振动传输率发现,等规构型的能带结构中仅有一条带隙(图4(c)),且振动传输率在此频率范围没有显著衰减,其振动模式主要为扭转振动。而间规构型的能带结构中出现多条宽频带隙(图4(d)),并且振动传输率在带隙中有较大的衰减。造成上述结果的原因是手性结构不同,间规构型将纵波转换为扭转波。利用结构的立构性转换和几何参数调整等方式能够有效抑制振动或弹性波的传播。
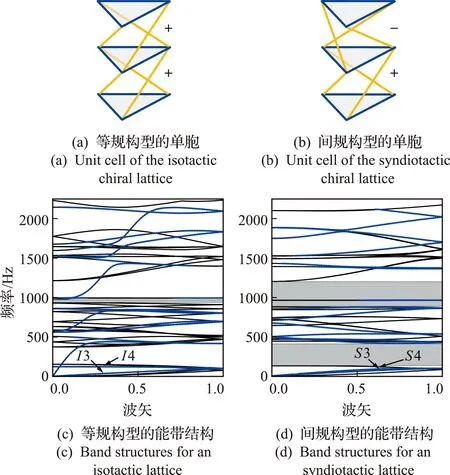
图4 手性晶格超材料的设计及其动力学分析
4.4 变刚度柔性结构设计与主动控制
随着航天器尺寸增大,航天结构自身的柔性特征愈发显著,在外界激励作用下结构极易发生弹性振动且难以衰减,影响航天器的姿态稳定。赋予超大型航天结构主动改变刚度的能力可以改善航天结构在超大尺度下固有的柔性缺陷。
An等[49]提出了一种基于颗粒串结构的变刚度方法(图5(a))。根据颗粒串结构弯曲过程中是否存在变形诱导刚化现象,提出了两种刚度提升机理,即颗粒串阻塞机理和拉伸增强颗粒阻塞机理。颗粒串阻塞利用球形颗粒组成的颗粒串结构,其中柔性绳的拉伸可以忽略不计;而拉伸增强颗粒阻塞则利用正方体颗粒组成颗粒串结构,弯曲过程中柔性绳拉伸。实验结果表明,设计的颗粒串阻塞结构最高可实现162倍的刚度提升(图5(b))。此外,利用3D打印技术进行颗粒阻塞结构的制造,并将其用于柔性结构的振动抑制[50]。实验与理论结果表明,增大压强差、增大颗粒腔横截面高度、减小颗粒尺寸和增大颗粒表面粗糙度均可以增强阻尼效应。
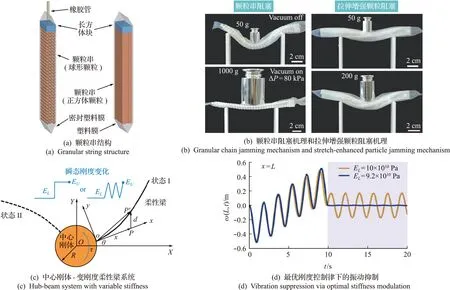
图5 变刚度柔性结构的设计与动力学分析
当航天器执行不同类型的任务时,可通过刚度切换实现对外界环境的实时响应。对于此类含参数切换的动力系统(图5(c)),基于Hamilton变分原理,建立了系统的耦合动力学模型,并利用保辛数值算法开展了变刚度主动控制研究[50]。利用提出的最优控制原理,柔性结构的残余振动可趋于零(图5(d))。
5 结 论
围绕超大型航天结构的动力学建模、数值计算、姿态控制、结构振动抑制和结构功能调控等难题,本文总结了团队近十年来在超大型航天结构在轨耦合动力学与姿态控制、超大型航天结构波动力学行为与控制和可展开结构设计与变刚度主动控制方法等方面取得的研究进展。目前仍有很多科学和技术难题有待突破。
(1) 超大型航天结构需要通过空间组装进行建造,然而其空间组装过程不仅面临空间环境干扰力的影响,也受空间机器人复杂操控力的干扰,而且组装过程中结构的尺寸、质量和转动惯量呈现阶跃性增长,控制系统构成不断发生变化,给动力学建模和控制带来困难。
(2) 超大型航天结构服役环境复杂,其振动和波动行为的调控需要结合航天结构的实际应用场景开展进一步研究。目前的研究工作主要是基于结构波动特性的被动隔振方法,而基于波动特性的实时和主动调控方法有待进一步研究。此外,超大型结构的波动和振动特性的地面原理性验证工作需要进一步开展。
(3) 在折纸型航天结构的设计和应用方面,还需要进一步研究折纸结构展开与卫星本体运动的耦合行为以及面板柔性以及环境摄动力对于在轨展开的影响。
(4) 现阶段的主动变刚度方面研究主要局限于地面模拟试验验证,未涉及空间复杂环境。在后续的变刚度结构设计中,需考虑太空环境的作用,例如真空、热和电/磁场等外激励,从而提出能够适应空间环境的刚度主动调控机理。
