计算最优控制辛数值方法

彭海军, 王 磊, 王昕炜, 吴志刚, 易雪玲

(1.大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室 工程力学系 大连 116024;2.大连理工大学 数学科学学院,大连 116024; 3.中山大学 航空航天学院,深圳 518000)

1 引 言

最优控制是现代控制理论的重要分支[1],在航空、航天、机械、机器人、化工、通信、能源和经济等领域有着广泛的应用,开发高效、高精度和高鲁棒性的控制算法具有重要实际价值和意义。20世纪60年代,Pontryagin极大值原理[2]和Bellman动态规划[3]方法有力地推动了最优控制问题解析法的发展。然而,对于复杂动态系统通常无法获得最优控制解析解,数值解法应运而生并成为主流。

最优控制问题的数值解法可以大致分为直接法和间接法。直接法将连续时间最优控制问题转化为一个大规模有限维非线性规划问题[4],如局部配点法[5]、全局配点法[6]和有限元法[7]等。直接法适用于不同类型、不同约束的最优控制问题,具有较大的收敛半径。缺点是当离散变量规模较大时,可能面临维数灾难[4];并且由于多数直接法不提供协态变量的信息,因此很难证明直接法的结果满足最优性条件。间接法主要求解由最优控制的一阶必要条件(FONCs)得到的Hamiltonian两点边值问题(HTBVP)或与其他方程的耦合[8],如打靶法、多重打靶法[9]和有限差分法[10]等。间接法基于最优性条件构造,因此求得的解至少是局部最优的;并且,由于间接法可得到协态变量的数值解,因此可以根据协态变量从本质上分析Hamiltonian动力系统的几何结构特征。间接法的缺点是,数值解的收敛半径较小,并且对于非常复杂的非线性最优控制问题,难以为没有实际物理意义的协态变量提供好的初始猜测。部分学者为融合上述两种方法优点,发展了混和求解策略,主要有两种常见方式,(1) 将直接法得到的结果作为间接法的初始猜测去求解[11];(2) 在直接法框架下,考虑将HTPBVP转化求解[12]。此外,得益于近年来人工智能(AI)技术快速发展,基于AI的数值算法也取得了长足的进步,如遗传算法[13]、粒子群算法[14]和微分进化算法[15]等。

最优控制问题固有地涉及Hamiltonian系统,而保辛方法是求解Hamiltonian系统的强有力工具。保辛算法保持了辛几何,可以有效地限制误差的增长,在动力学系统的长时间模拟上具有独特的优势。保辛方法不仅可以在离散后继承原连续系统的固有辛结构,而且可以精准地反映系统的能量变化水平[16],求解精度高,因此具有重要的实际意义。

由于保辛方法的重要意义,学者们从间接法和直接法的框架出发,发展了最优控制问题的保辛方法。间接法本身会涉及到Hamiltonian系统,因此构造保辛方法具有天然的优势。文献[17,18]基于生成函数提出了保辛方法,通过生成函数满足Hamiltonian系统正则变换下的条件,实现对HTBVP的求解。Sanz-Serna等[19]将保辛Runge-Kutta法用于求解HTBVP。此外,也有学者从直接法的框架出发构造了保辛直接法。这类方法对最优控制问题的动力学方程进行保辛离散,可以在求解时实现对原动力系统更精确的近似。如Bonnans等[20]提出的Runge-Kutta差分格式的保辛离散,Ober-Bloebaum等[21]提出的结合零空间方法的保辛方法等。其中最具代表性的是离散力学与最优控制(DMOC)方法[22]。该方法对动力学方程进行保辛离散,然后离散性能指标和其他约束,将原问题转化为NLP问题再求解。但DMOC方法只考虑了动力学方程的保辛,这种保辛是不完全的。

近年来,本课题组针对不同类型的最优控制问题,提出了一系列保辛数值方法,并将其应用在了航空航天和机械等各个领域。本文分别针对常微分方程(ODE)和微分代数(DAE)方程的最优控制问题,考虑了含约束、时滞和切换系统的情况,给出了相应保辛求解方法。进一步,面向实际场景中闭环控制需求,介绍了保辛算法在模型预测控制、滚动时域估计和瞬时最优控制等技术中的应用。

2 常微分方程最优控制问题的辛数值方法

针对动力学方程为常微分方程的最优控制问题,考虑了一般无约束问题、含不等式约束以及含时滞问题的保辛数值解法。

2.1 一般无约束问题的辛离散

文献[23]针对一般非线性最优控制问题,提出了高精度和高效率的保辛数值算法,基于对偶变分原理和生成函数方法,将其转化为非线性方程组进行求解。此外,还可以先通过拟线性化方法[24]将问题转化为一系列线性二次(LQ)问题,再通过上述方法将其转化为线性方程组求解。

2.1.1 问题列式

考虑无约束非线性最优控制问题(P2-1),

x(0)=xs

(1)

式中x(t)∈ns和u(t)∈nu分别为状态变量和控制变量,f:ns×nu×→ns为系统方程。

引入协态变量λ(t)∈ns,问题(P2-1)的Hamiltonian函数定义为H=L+λTf(x,u,t)。

根据变分法推导问题(P2-1)的必要条件可得∂H(x,u,λ,t)/∂u=0,则可求得u(t)=g(x(t),λ(t))。在给定控制时域(0,tf)内,定义作用量

(2)

由最小作用量原理,可以推导出问题(P2-1)的FONCs满足如下Hamiltonian正则方程,

(3)

至此,非线性最优控制问题(P2-1)通过变分原理转化为非线性HTBVP。

2.1.2 基于对偶变分原理的辛算法

(4)

选择式(4)中不同的状态变量和协态变量作为独立变量,可以得到不同的生成函数。然而,根据非线性最优控制问题得到Hamiltonian系统,其作用量并不能解析得到,且生成函数只能根据数值近似的作用量得到。因此,为了构造生成函数来近似Hamiltonian系统,作用量的数值近似值需要充分接近解析值,并保持正则变换。

本文基于四种生成函数和最小作用量原理,构造了求解HTBVP的辛数值方法。

(5)

基于最小作用量原理,若Hamiltonian正则方程在时域内得到满足,那么作用量(即第一类生成函数)是关于两端状态的函数,则可得第j个子区间内近似第一类生成函数的驻值条件

(j=1,2,…,Q)

(6)

(j=1,2,…,Q)

(7)

整个时域内的近似第一类生成函数的驻值条件表示为

(j=1,2,…,Q-1)

(8)

整个时域两端的协态变量为

λ0=-∂S/∂x0,λQ=∂S/∂xQ

(9)

至此,基于最小作用量原理,原非线性最优控制问题(P2-1)转化成了非线性代数方程(6～9)。

最后采用牛顿法等数值算法迭代求解非线性方程组。注意,为了加快牛顿法收敛速度,需要求出Jacobi矩阵的解析形式,得到的Jacobi矩阵具有稀疏对称特性和较小的带宽,采用稀疏线性求解器可以进一步加快计算效率。

2.1.3 保辛序列迭代算法

此外,还可以通过文献[25]中保辛序列迭代算法求解。首先根据拟线性化方法,将一般的非线性最优控制问题转化为一系列LQ问题;然后由参变量变分原理和保辛离散,将LQ问题转化为线性方程组;最后求解线性方程组,得到问题的解。

拟线性化方法对状态方程和不等式约束进行线性化,将性能指标展开至二阶,将非线性最优控制问题(P2-1)转化为一系列的LQ问题的迭代,其收敛性不依赖于迭代初值的选取[24]。而且,拟线性化方法可以提高收敛速度,同时避免了对没有明确物理意义的协态变量提供初始猜测。

设第(k+1)次迭代的LQ问题如下,

w[k](t)

x[k+1](0)=xs

(10)

(11)

w[k](t)=f(x[k],u[k],t)-A[k](t)x(t)-

B[k](t)u(t)

(12)

用符号(•)[k]表示变量第k次迭代的计算结果。将得到的LQ最优控制问题反复迭代求解,直至满足‖x[k]-x[k+1]‖/‖x[k+1]‖≤ε,得到最优解。

按照2.1.2节的方法,基于第一类生成函数和变分原理,将LQ问题转化为线性方程组,最后用数值方法求解。

注：由作用量变分原理知,满足Hamilton正则方程。因此,Hamilton系统的辛相流结构在离散时间点上得到保持。由于每一次迭代的LQ问题都是用保辛算法求解,故基于序列迭代的方法自然也是保辛的。

2.2 含不等式约束问题的辛离散

工程中涉及的最优控制问题通常要考虑复杂约束。文献[26]针对动态系统、约束以及性能指标均为非线性的最优控制问题,基于第二类生成函数、参变量变分原理和多区段LGL型伪谱近似,提出了一种多区段保辛伪谱算法(SPM)。

2.2.1 问题列式

考虑含不等式约束最优控制问题(P2-2),

x(ts)=xs

h(x,u,t)≤0

(13)

式中h:ns×nu×→nh为nh维不等式约束。

2.2.2 问题转化

序列拟凸化方法(SCvx)[27]是拟线性化方法的一种。由SCvx,问题(P2-2)转化为一系列LQ问题的迭代。根据参变量变分原理,推导得LQ问题的一阶必要性条件为以下关于状态变量和协态变量的线性Hamiltonian 两点边值问题和一个关于参变量的线性互补问题(LCP)的耦合,

(14)

α(t)≥0,μ(t)≥0,μT(t)α(t)=0

(15)

2.2.3 多区段保辛伪谱算法

求解含不等式约束的LQ问题的SPM与2.1节的方法类似。首先对控制时域进行离散,每个子区间内的状态变量、协态变量和参变量用LGL伪谱法进行插值;基于第二类生成函数和参变量变分原理,问题转化为一个线性代数方程组和一个LCP的耦合,构成一个混合线性互补问题;用Lemke’s方法求解LCP,得到问题(P2-2)的解。

LCP计算过程中,系数矩阵具有稀疏性,并且部分矩阵还具有对称性,因此计算效率高。整个算法基于最小作用量原理构造,保证了算法中涉及到的线性代数方程组的系数矩阵是稀疏对称的,且其半带宽仅与动力学系统的维数及所有子区间内采用的伪谱法的最高阶数相关。

2.3 含时滞问题的辛离散

工程问题中的时滞可以存在于状态变量和控制变量中,但在间接法的框架下,求解含控制时滞的问题会变得很复杂。文献[28]针对一类无约束的状态时滞最优控制问题,基于第一类生成函数,在对偶变分原理和局部LGL型伪谱近似的框架下,提出了一种多区段保辛伪谱算法。

2.3.1 问题列式

考虑含时滞的最优控制问题 (P2-3),

x(t)=g(t) (t∈[ts-θ,ts])

(16)

式中θ∈+为状态变量的时滞量,g(t)∈([ts-θ,ts],ns)为初始状态,假设g(t)≡xs。

2.3.2 问题转化

通过SCvx,问题(P2-3)转化为一系列含状态时滞的LQ最优控制问题的迭代。由变分原理推导得到时滞LQ问题关于状态变量和协态变量的最优性条件为HTBVP

(t∈[ts,tf])

(17)

(18)

式(17,18)中系数矩阵的具体表达见文献[28]。HTPBVP呈现了分段的特点,其既包含超前的协态变量,还包含滞后的状态变量。

注：对含不等式且性能指标不是二次型的时滞最优控制问题,可通过SCvx方法将其转化为带约束的线性二次问题。然后推导其一阶必要条件,得到一个分段HTBVP和一个关于参变量的LCP的耦合问题。一方面,HTBVP中,右端项存在参变量;另一方面,LCP中,参变量和状态变量、协态变量相关。可以发现,拟线性化后的问题仅在HTBVP中存在分段特性。因此,可以采用与2.2节类似的方法,基于第二类生成函数构造相应的多区段保辛伪谱算法。

2.3.3 多区段保辛伪谱算法

求解含时滞的HTBVP的整体方法与2.1.3节的方法类似。

首先将控制时域[-θ+ts,tf]均匀离散,再用LGL伪谱法插值。对每个子区间,基于第一类生成函数和参变量变分原理,可以得到每个子区间上的方程组。由于时滞的存在,子区间上的第一类生成函数,对当前子区间内状态变量的变分将与超前子区间内的协态变量发生关系;对当前子区间内协态变量的变分将与滞后子区间内的状态变量发生关系。然后,对全局的第一类生成函数施加变分原理,将LQ问题转化为线性代数方程组,最后求解方程组,得到问题(P2-3)的解。

3 微分代数方程最优控制问题的辛数值方法

机械和化工等领域中出现的动力学系统往往可描述为微分代数方程,这些方程在形式上一般都属于半显式微分代数方程。

针对动力学方程为微分代数方程的最优控制问题,本节考虑了无约束、含不等式约束以及含切换系统的最优控制问题的保辛数值解法。

3.1 无约束半显式DAE最优控制问题的辛离散

半显式微分代数方程由微分方程和代数方程组成。半显式微分代数方程的数值求解与普通的常微分方程相比,其代数方程需要在整个时域内得到严格满足。如果不能得到高精度满足,那么整个结果是不精确甚至失真的,这会加大最优控制中在线控制的负担,甚至控制失效。另一方面,数值求解时形成的非线性方程组的稀疏矩阵可能出现病态,往往会导致收敛困难甚至失败,进而导致整个问题求解失败。基于上述困难,目前对于微分代数方程最优控制问题的求解研究较少。

文献[29]针对半显式微分代数方程最优控制问题提出一种保辛间接解法,从间接法的框架出发,基于变分原理和生成函数性质,对问题的必要条件进行保辛离散,将必要条件转化为非线性方程组;最后采用迭代策略求解非线性方程组。

3.1.1 问题列式

考虑半显式微分代数方程最优控制问题(P3-1),

0=g(x,y,u,t)

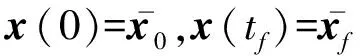
(19)

式中g:nx×ny×nu×[0,tf]→ny为代数方程的右端项函数。注意,上述方程并不直接出现代数变量对时间的导数将代数方程对时间求导并利用微分方程才会出现

定义增广Hamiltonian函数,

(20)

式中λg∈ny为代数乘子。由变分原理,推导得到问题(P3-1)的必要条件为一个HTBVP,

(21)

(22)

(23)

3.1.2 保辛间接法

按照2.1.2节的方法,基于第四类生成函数和变分原理,将HTBVP保辛离散为非线性方程组。最后,通过迭代策略求解非线性代数方程组,得到问题(P3-1)的解。

本节的保辛间接法主要有以下优势, (1) 迭代求解方程组时,需要求解其Jacobi阵,由变分原理可知Jacobi矩阵为稀疏对称阵。在每一步迭代更新未知量时,利用对称性可快速得到整个Jacobi阵。同时,稀疏性降低了计算所需内存。因此,该方法可以高效和低成本地求解大规模问题。(2) 此方法保持了原始Hamiltonian系统的辛结构。求解时,解的最优性条件和问题的代数方程均能高精度满足。将所得控制施加于系统,系统能精确转移至对应的终端状态。(3) 与直接法相比,保辛间接法收敛速度快,计算时间短,且在初始猜测发生改变时,收敛速度也不会受到影响。

3.2 含不等式约束的DAE最优控制问题的辛离散

针对含不等式约束的半显式微分代数方程最优控制问题,文献[30]提出了保辛间接法。基于第四类生成函数,将问题的必要条件构成的耦合问题保辛离散,再用非光滑方法将其转化为非光滑方程组,最后通过一种复合求解策略求解非光滑方程组。

3.2.1 问题列式

考虑含不等式约束的微分代数方程最优控制问题(P3-2),

0=g(x,y,u,t)

h(x,u,t)≤0

(24)

式中h:nx×nu×[0,tf]→nh为nh-维不等式约束。推导可得问题(P3-2)的必要条件为一个HTBVP与LCP的耦合,

(25)

(26)

β≥0,h(x,u(x,λ,y,λg,β,t),t)≤0

(27)

βTh(x,u(x,λ,y,λg,β,t),t)=0

(28)

3.2.2 保辛间接法

求解含不等式约束的微分代数方程最优控制问题的保辛方法,与第2.1.2节的方法类似,基于第四类生成函数和变分原理,将问题(P3-2)必要条件形成的HTBVP与LCP的耦合问题,离散为一个非线性方程组与一个LCP的耦合问题。

这类耦合问题也称混合非线性互补问题(MNCP)[31],由于问题中非线性方程组与互补条件耦合,因此难以直接求解。为了便于求解离散后的耦合问题,首先利用非光滑F-B(Fischer-Burmeister)函数将其转化为一系列非光滑方程组。然后,用替代矩阵替代不存在的Jacobi矩阵进行迭代计算。替代矩阵是稀疏的,且其中一部分元素是对称的,因此对于大规模的问题,也可以高效求解。最后采用包含预迭代技术的复合求解策略求解,得到问题(P3-2)的解。预迭代技术可以提高初始解的质量,能快速得到收敛的解。并且当初始解改变时,其收敛速度不会受到较大影响。

3.3 切换系统最优控制问题的辛离散

与一般连续系统相比,切换系统最优控制问题更加复杂,求解更加困难。由于切换的存在,切换系统最优控制问题的最优性必要条件将变得很复杂,不利于数值求解[32]。因此针对切换系统最优控制问题,提出了保辛直接解法,通过参变量变分原理和生成函数的性质,发展了一种基于辛离散的切换系统离散格式。将切换系统动力学方程和整个最优控制问题保辛离散为非线性规划问题,最后求解非线性规划问题。

3.3.1 问题列式

考虑含切换机械系统的最优控制问题(P3-3),

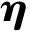
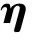
(29)

该问题是一类含不等式约束的微分代数方程最优控制问题。

3.2.2 保辛直接法

问题(P3-3)采用保辛直接法求解。首先对整个时域进行均匀剖分。由参变量变分原理,可以将每个子区间上的动力学方程进行保辛离散。保辛离散可以使其较好地模拟原系统的特性。进一步离散整个最优控制问题,将问题(P3-3)转化为一个含等式约束和不等式约束的大规模NLP问题。最后采用优化求解器求解,得到原问题的解。求解后可以直接得到参变量随时间的变化规律,这样也就得到整个系统运动过程中的切换规律。

4 闭环最优控制问题的辛数值方法

前两节提到的保辛解法可以用于不同类型的轨迹规划问题,但其都是开环算法,不存在反馈。在实际控制任务中,由于各种扰动的存在,开环算法可能导致系统的真实轨迹偏离设定轨迹。基于此,在离线规划后,可通过闭环控制算法实时跟踪参考轨迹来处理这类问题。

针对闭环最优控制问题,利用第2.2节的SPM,本节构造了求解闭环最优控制问题的保辛模型预测控制(MPC)[33]、保辛滚动时域估计(MHE)[34]以及保辛瞬时最优控制(IOC)算法[35]。

4.1 保辛MPC算法

MPC是一种基于滚动思想的算法。在每个采样时刻以当前状态作为初始状态,求解一个有限时域的开环最优控制问题,并将求解的最优控制中的第一步作为当前控制窗口的控制输入。如果想在快速变化的系统中应用MPC,需要在每个采样步求解最优控制问题时具有较高的求解效率。而第2.2节的保辛伪谱法具有收敛速度快和求解效率高的特点。文献[33]基于保辛伪谱法构造了保辛伪谱MPC算法。

4.1.1 问题列式

h(x,u,t)≤0

(30)

4.1.2 保辛MPC算法

保辛MPC控制器可以概述为以下过程。

4.2 保辛MHE算法

闭环控制过程中需要精确地获得系统的当前状态。但工程中的大多数问题通常不能直接获得其全部的状态,因此需要进行状态估计,根据可测的已知的状态变量来确定所有的状态变量。这类问题可以采用滚动时域估计算法来求解。其基本思想是在每个采样时刻,根据过去的采样数据和估计结果,求解一个过去有限时间内的优化问题。通过求解优化问题,得到过去有限时间内的虚拟状态轨迹。将虚拟状态轨迹中当前时刻的状态值作为当前采样步的状态估计值。

MHE问题通常认为是MPC的对偶问题,对于需要高频采样的机械系统,需要较高的在线计算效率。在MHE中,如果把模型误差看作控制变量,则每个采样步需要求解的问题可以视为一个含不等式约束的最优控制问题。该问题可以用保辛伪谱法求解,基于此,文献[34]构造了求解滚动时域最优控制问题的保辛伪谱MHE算法。

4.2.1 问题列式

y=g(x,n,t)

h(x,u,t)≤0

(31)

对于每个采样时刻的估计问题,均可看作是一个开环最优控制,可以采用保辛伪谱法进行求解。

4.2.2 保辛MHE算法

保辛MHE控制器可以概述为以下过程。

MHE和MPC都可以在含不等式约束下的非线性最优控制问题框架下求解,这给控制软件在硬件上的实现带来了极大的便利。

4.3 保辛IOC算法

机器人多体系统轨迹跟踪控制问题可以表述为微分代数方程的瞬时最优控制问题。文献[35]针对瞬时最优控制问题,构造保辛IOC算法。

4.3.1 问题列式

瞬时最优控制在每个瞬时构造目标函数。假设tk时刻待求解的最优控制问题(P4-3)为

(32)

4.3.2 保辛IOC算法

保辛IOC算法可以总结如下。

采用Newton-Raphson方法迭代求解瞬时最优控制问题。在每个时刻t=tk,将微分代数方程保辛离散,转化为非线性代数方程组。将tk时刻的状态xk作为迭代的初值。根据瞬时最优控制理论得到瞬时最优控制uk,再将uk作为新的控制输入,更新当前状态xk+1,直至相邻两步的状态变量小于给定的收敛误差,IOC过程结束。

5 保辛最优控制方法的应用

保辛最优控制方法已在各个领域得到了广泛的应用,涵盖了海陆空天等各个方面。

(1) 航天领域的应用。近地轨道卫星编队重构问题[36]可以转化为非线性最优控制问题,采用2.1节的基于第三类生成函数的辛算法求解。文献[36]针对这类问题,在算例1中,将保辛算法和Gauss伪谱法计算得到的状态与控制变量的相对误差和计算时间分别进行对比,结果列入表1和表2。其中,符号—表示由于离散段数过多导致Gauss伪谱方法无法求解。由表1和表2可知,保辛方法在状态变量和控制变量的求解精度上以及求解效率上明显高于Gauss伪谱法。

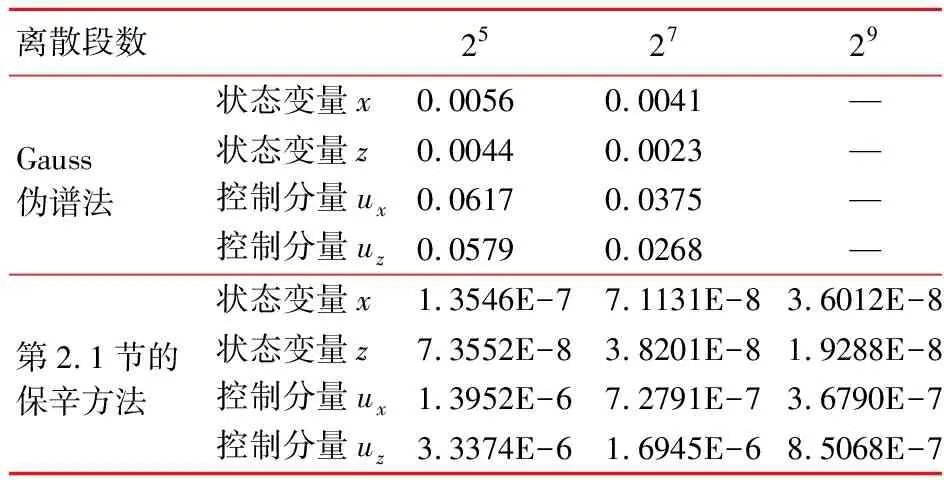
表1 保辛算法与Gauss伪谱法计算精度比较

表2 保辛算法与Gauss伪谱法计算效率比较 (单位:s)

航天器在日月系统L2平动点附近Halo轨道的状态估计问题[37]可以采用第4.2节的保辛MHE算法求解。文献[37]的算例1将保辛MHE算法与经典的EKF和UKF滤波算法进行了对比,结果如图2所示。可以看出,保辛MHE算法可以有更精确的估计结果。

(2) 海上装备的应用。舰载机着舰问题也可以转化为最优控制问题,通过保辛方法求解。文献[38]针对模型参数不准确条件下的全自动着舰控制问题,提出了一种基于保辛伪谱法的自校正MPC[38]方法。将保辛MPC与传统的极点配置算法和LQR控制算法进行了对比,跟踪效果如图3所示。可以看出,保辛MPC可以更精确地跟踪甲板运动,完成高度轨迹的跟踪控制。

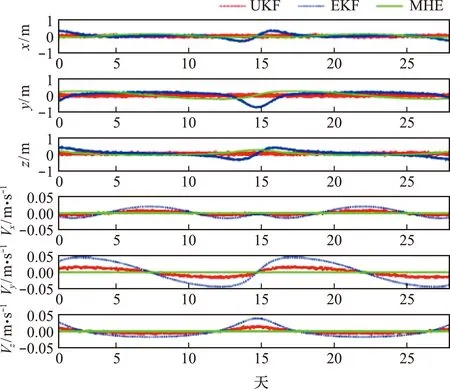
图2 EKF,UKF和MHE的误差估计

图3 自校正MPC算法与传统控制算法甲板运动轨迹跟踪效果对比

舰载机调运问题可以转化为非线性最优控制问题,通过保辛方法求解。文献[39]针对无杆牵引系统舰载机甲板路径规划问题,提出了牛顿迭代保辛伪谱算法NSP,并将NSP方法与典型的伪谱法进行了对比,轨迹如图4所示,相同参数设置下的计算结果列入表3。从图4可以看出,舰载机3和舰载机5的NSP方法所得路径长度明显短于伪谱法的路径长度。由表3可知,NSP算法计算时间明显小于伪谱法,计算效率上有更大的优势。

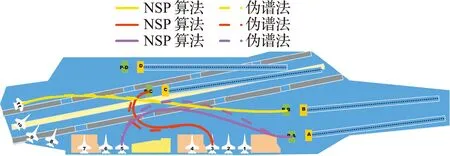
图4 舰载机的滑行轨迹

表3 NSP算法与伪谱法计算结果比较

(3) 陆地装备的应用。拖挂车系统轨迹规划问题可以描述为含不等式约束的微分代数方程最优控制问题,针对单节拖挂车系统的轨迹规划问题,文献[40]采用3.2节的保辛方法求解,并与GPOPSII的结果进行了对比,计算结果列入表4。由表4可知,保辛方法可以收敛至更精确的性能指标,迭代次数和CPU时间低于GPOPSII,并且具有更强的鲁棒性。

对于桥式起重机的运动控制问题[41],可以采用离线轨迹规划+在线轨迹跟踪的策略求解。离散轨迹规划阶段采用SPM求解。在线轨迹跟踪阶段采用4.1节的保辛伪谱MPC求解。两个阶段都可以在统一的保辛伪谱算法框架下求解,这极大方便了控制算法在硬件上的集成。文献[41]测试了保辛伪谱MPC控制器在各种外界扰动下的鲁棒性,并与部分反馈线性化PFL控制器进行了对比,图5给出了两种方法的状态变量曲线。可以看出,保辛MPC可以更有效地跟踪参考轨迹。

图5 存在外界扰动情况下桥式起重机状态变量的曲线

(4) 其他领域中的应用。化工生产中的间歇式反应容器优化问题可以转化为微分代数方程最优控制问题。针对间歇式反应容器优化问题,文献[42]采用3.1节的保辛方法求解,并与GPOPSII对比,测试了保辛方法的鲁棒性。两种方法在不同随机水平的初始猜测下收敛所需迭代步数的均值和方差列入表5。由表5可知,保辛方法对初始猜测解具有更强的鲁棒性。

表5 随机初始猜测解下保辛方法与GPOPSII的 迭代步数

化工装备中两罐式 CSTR 系统的温度控制问题是一类含时滞的最优控制问题。文献[43]的算例3采用2.3节的保辛伪谱法求解,并对比了在不同时滞量下,保辛方法和迭代动态规划IDP方法的求解结果,列入表6。由表6可知,保辛伪谱法收敛速度更快,求解精度高。

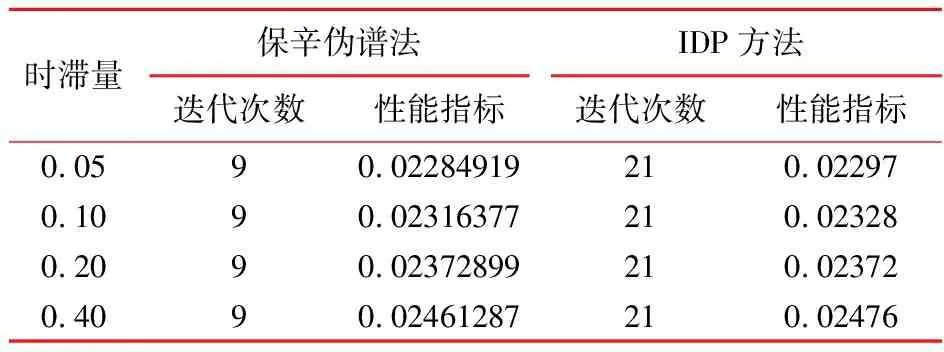
表6 化工温度控制问题保辛方法与IDP方法的 迭代次数和性能指标

6 结 论

本文针对常微分方程、微分代数方程和闭环最优控制问题,综述了保辛数值方法。对于ODE最优控制问题,基于生成函数和变分原理提出了保辛方法,该方法适用于无约束、含不等式约束和含时滞问题,具有快速收敛的特点。对于DAE最优控制问题,采用保辛间接法处理无约束以及含不等式约束的问题,并用保辛直接法求解了含切换系统的问题。对于闭环最优控制问题,提出了保辛MPC、保辛MHE和保辛IOC算法。保辛方法已经成功应用于航空航天和机械等各个领域。

基于目前的研究还可以进一步考虑以下三个方面的工作。

(1) 轮式移动机器人和无人机等装备自身或实际环境中会存在大量不确定性,因此研究不确定性条件下机器人的轨迹规划问题是有必要的。

(2) 对于无法精准动力学建模的实际复杂系统,可以与人工智能结合来解决无模型系统最优控制问题。

(3) 保辛方法可以与硬件系统结合,在特定的硬件环境上开发和构建软件系统,进行嵌入式的开发,将保辛算法集成在硬件上。