平面刚体系统的参数预调节保辛算法

吴志刚, 徐小明

(中山大学·深圳 航空航天学院,深圳 518107)

1 引 言

多体系统的动力学模型通常采用两种坐标描述方法,即最小坐标与非最小坐标[1]。与最小坐标相比,非最小坐标具有数学表达方便、简洁以及方法通用性强等优势。但是,非最小坐标描述不可避免地引入了代数约束条件,导致其数学表达为微分代数方程组。与常微分方程相比,微分代数方程组的数值求解相对复杂,面临着约束违约和刚性方程问题等,其数值计算的精度与稳定性受到严峻考验[2]。因此,相关问题的数值计算方法研究一直是多体系统动力学研究的重要课题。

近几十年,在多体系统动力学的应用背景下,微分代数方程组的计算方法得到了快速发展[3]。对于约束哈密顿系统,保辛算法可以较好地处理约束违约与刚性方程问题,取得了良好的计算稳定性与精度[4,5]。然而,经典的数值计算格式存在累加的能量耗散和相位误差问题。虽然辛算法通过保证离散过程的辛对称性,进而在数值计算过程中保持了系统的守恒律,解决了能量耗散问题,但相位误差随时间快速积累导致算法精度仍受到极大的影响[6]。Reich[7]很早就通过误差估计分析了单步辛算法相位误差产生机制。邢誉峰等[8]较早地阐述了算法的累积相位误差,并针对单自由度线性系统提出了单步保辛算法相位误差的修正公式。随后,多位学者提出了保辛算法的相位误差补偿方法[9-14]。但这些方法没有推广应用于约束哈密顿系统。最近,Noh等[15-17]分析了算法相位误差随时间累积的问题,称这种现象为算法的弥散性(Dispersion),并指出能量的耗散性和相位的弥散性都可以通过设定隐式积分格式的待定参数来改变,恰当的参数取值可以使积分算法在仿真分析中给出更为精确结果。然而,该方法的待定参数与离散方式相关,改变其取值将破坏积分格式的原有结构(如辛结构),因此不能直接应用。

本文针对非最小坐标描述的平面刚体系统,展开具有低相位误差积累特点的保辛积分构造方法研究。首先,本文采用笛卡尔坐标描述刚体的平移与旋转运动。这是一种非最小坐标描述,导致相关动力学模型的质量矩阵表达形式的不唯一性[18]。本文通过引入正交投影矩阵(Orthogonal Projection),将系统的质量矩阵描述为关于待定参数的等价表达式,进而推导出了改进的拉格朗日方程[19]。研究发现,离散过程中关于待定参数的项将产生额外的数值误差。通过调整参数的大小和正负,进而调整相关误差的大小和方向,可以达到抵消系统其他项误差的效果,从而大幅降低数值方法相位误差随时间累积的速度。由于该方法中的待定参数是在推导动力学方程过程中得到的,与离散过程无关,所以待定参数取值的改变并不会破坏数值积分格式原有的离散性质。利用这一思想,本文针对平面刚体系统,提出了预参数调节保辛积分格式的构造方法。数值结果表明,该方法在保持保辛积分格式无能量耗散、长时间积分稳定的情况下,同时大幅降低了离散系统的相位误差,极大程度上改善了数值方法的轨迹精度。由于非最小坐标描述中质量矩阵的不唯一性普遍存在,所以该方法不仅可以用于平面刚体系统,还可以推广到其他约束多体系统。

2 改进的拉格朗日方程

2.1 Lagrange方程描述

当采用非最小坐标描述平面刚体运动时,选取的广义坐标维度大于独立运动自由度数,其动力学方程可以表达为Lagrange方程形式

(1)

Φ(q)=0

(2)

式中q∈n为n维广义坐标,p∈n为广义动量,T为动能,Fex∈n为外力,Φ∈m为m个完整约束,A=∂Φ/∂q为约束的雅克比矩阵,λ∈m为拉格朗日乘子。假设动能的具体表达式为

(3)

式中M(q)∈n×n为n维质量矩阵。对于约束系统,质量矩阵一般为半正定矩阵。由解的存在唯一性条件,其矩阵的秩满足[18]

rank(M)≥n-m

(4)

根据动能表达式(3),系统的广义动量可以表达为

(5)

实际上,上述动能表达式与唯一性条件表明,质量矩阵中只有投影到n-m维约束零空间中的分量对动能产生正的作用,而投影到m维约束空间中的分量只能产生零动能。在物理上,任何可能的运动(即满足约束方程的运动)都不可能与零动能相关联。这暗示了约束系统质量矩阵的不唯一性。

2.2 基于正交投影的等价表达式

为将质量矩阵表达为关于待定参数的等价形式,定义约束的零空间矩阵

N(A)={z∈n:Az=0}

(6)

则可以定义S∈n×n为N(A)上的正交投影矩阵,满足R(S)=N(A),S2=S,以及S2=S,其中R(S)为矩阵的值域(Range of the matrix)。根据正交矩阵定义,可以推导得到其正交补矩阵为I-S,对任意满足其中I为单位矩阵。这样就可以定义质量矩阵的等价表达式

Mγ(q)=M(q)+γ(I-S)

(7)

式中γ为任意参数。将式(7)代入式(3)替换质量矩阵M,可得具有待定参数的等价动能表达式

(8)

与式(3)的质量矩阵相比,式(8)增加了与参数γ相关的项,其只能产生零动能,不会对系统的真实运动状态产生影响。将式(8)代入式(1),可以得到Lagrange方程的等价表达式

(9)

式中 广义动量p已经重新定义为

(10)

式(9)称为改进的拉格朗日方程MLEs(Modified Lagrange’s equations)。

3 参数预调节保辛算法思路

文献[19]阐述了改进的拉格朗日方程中与参数γ相关的广义约束力项的离散误差产生机制。误差分析与数值结果表明,当满足一定的离散条件,参数γ相关项将产生额外的数值误差。通过预先调整参数γ的取值,可以抵消数值积分产生的误差。受此启发,本文提出利用改进的拉格朗日方程构造具有低相位误差累积的保辛积分方法,具体思路如下。

(1) 在Lagrange框架或Hamilton框架下推导系统的动力学方程,得到原始的质量矩阵,如式(1～5)所示。

(2) 根据约束方程的具体形式,推导约束零空间上的正交投影矩阵S,得到其正交补映射I-S,进而构造具有待定参数的质量矩阵与动能表达式,如式(7,8)所示。

(3) 在上述公式基础上,推导改进的拉格朗日方程,如式(9,10)所示。

(4) 联合改进的拉格朗日方程与约束方程,构造保辛算法。

(5) 通过先验误差估计或后验误差估计,得到使得相位误差显著降低的待定参数取值。

在进行参数预调节算法构造时,需要注意以下几点,离散格式可以采用针对指标-3微分代数方程组的任意一种保辛格式,如辛龙格库塔法或变分的算法等;待定参数是在仿真前选取的,仿真中不再改变。当采用后验误差估计方法确定待定参数γ取值时,本文首先假设轨迹误差δW是参数γ的线性函数,计算两个参考点(γ1,δW1)与(γ2,δW2)的值,然后令δW=0,通过线性插值就可以得到γ的估计值

γopt=(γ1δW2-γ2δW1)/(δW2-δW1)

(11)

即为使得轨迹误差为零的最优参数。在选取参考点时,γ1一般可选为零,γ2可选为平面刚体系统转动惯量或质量矩阵相关的常值,然后通过短时间仿真计算得到相应的后验误差值δW1与δW2,然后再将参考点的值代入式(11),求取最优参数值γopt。文献[20]更为详细地介绍了确定待定参数γ的后验误差估计方法,限于本文篇幅不再介绍。

4 平面刚体系统建模

4.1 单刚体系统

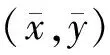
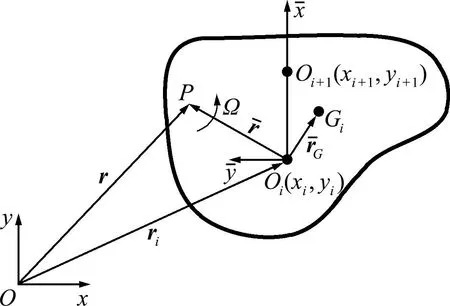
图1 笛卡尔坐标描述的平面刚体

xi=[xiyixx+1yi+1]T

(12)

与单位正交矢量

ui=Di1xi,vi=Di2xi

(13)

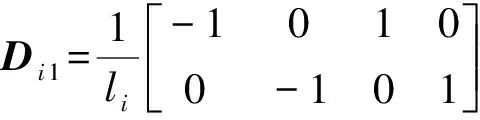
(14)

并且需要满足约束条件

(15)

根据式(13),可以定义平面运动的刚体旋转矩阵

此外，对微博的良好管理，离不开对网络技术的掌握。地方政府可以向官员组织开设微博的相关课程，使地方政府官员熟知微博各项操作的具体方法，做到准确地使用微博，避免因操作失误引起误会，影响政府官员微博的公信力。

Ri=[uivi]

(16)

这样全局坐标系下刚体的质心坐标可表示为

(17)

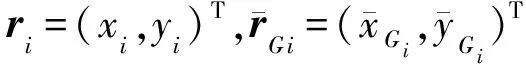
(18)

据此可以推导得到单刚体的动能表达式

(19)

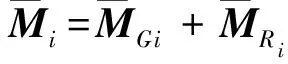
(20)

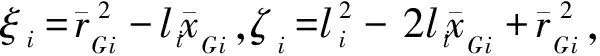
(21)

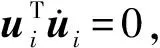
(22)

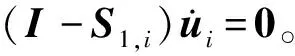
(23)

将式(13)代入式(23),可以得到单刚体的等价动能表达式

(24)

(25)

4.2 重力场中的多体平面摆

为简化推导过程,本文只考虑如图2所示平面多体摆系统,其中Oi是平面铰连接,坐标为(xi,yi),点O0的坐标为(0,0)。定义系统的广义坐标向量为

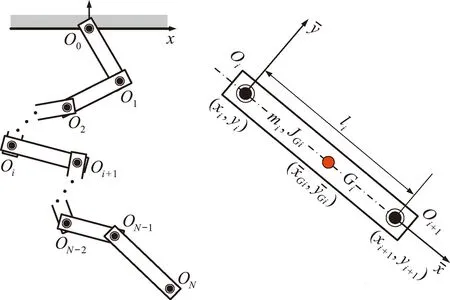
图2 多体平面摆

q=[x1y1…xNyN]T

(26)

其满足约束方程

(27)

刚体系统的总动能表达式为

(28)

(29)

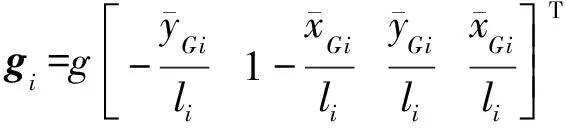
(30)

重力加速度g=9.81 m/s2。然后可以推导得到系统的外力Fex=-∂V/∂qT。

为获得式(28)中参数γ的合理取值,可以定义参数[21]

(31)

为所有平面刚体转动惯量的均值,离散误差估计表明当γ=γR时,数值积分的离散旋转动能误差较小。进一步,还可以考虑减小平移动能的离散误差,此时可以定义

(32)

5 数值算例

考虑由两个刚体组成的两自由度平面摆,其构型参数为l1=2,l2=3,m1=m2=1以及

(33)

式中i=0,1。给定初始条件

(34)

本文采用Gauss-Lobatto SPARK算法来构造保辛积分格式,具体格式参考文献[22]。需要注意,由于式(28)的引入,保辛积分格式中含有待定系数γ。首先取待定系数γ=0与γ=γT=0.916667进行数值结果比较,其中γT的定义见式(32)。为此,定义均值误差

(35)

(36)

(37)

式中Nh为总的时间步数,N=2为刚体数目,h为时间步长,δ(#)表示数值解和参考解之间的误差,H=T+V为系统的能量,上标k表示tk=hk时刻的值。本文参考解选取为比待比较数值解步长小100倍的数值解。

表1给出了当待定参数γ取0与取γT时的数值比较结果,其中h=0.04,Nh=100,(s,s)代表SPARK方法选取了s个Gauss-Lobatto积分点与s个Lobatto积分点进行离散。若数值积分选取s个积分点,则收敛阶数为2s阶。数值结果显示,对于2阶、4阶、6阶和8阶SPARK方法,参数γ=γT时的轨迹精度与能量精度均优于γ=0。证实了参数预调节保辛算法可以通过调整γ的取值改变数值积分的精度。图3给出了能量误差随步长收敛曲线,其中s=1。可以看出,无论参数取何值,取1个积分点的SPARK方法都保证了2阶收敛性。实际上,当s=2,3和4时,数值结果也显示了算法与待定参数γ取值无关的2s阶收敛性,限于篇幅本文不列出其相关数值结果。

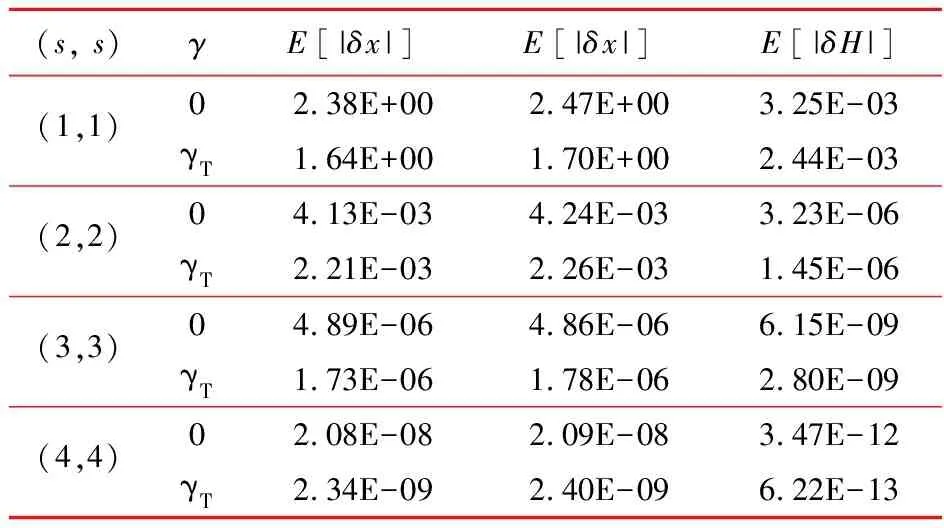
表1 数值结果比较

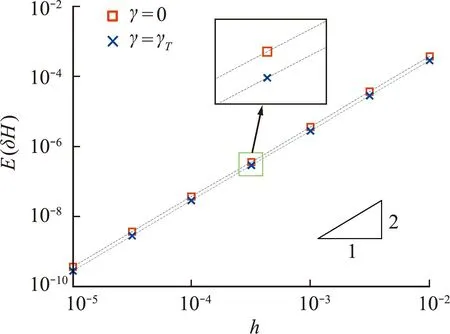
图3 能量误差随步长收敛曲线

图4呈现了数值误差随待定参数γ变化曲线,其中h=0.04,Nh=100,数值误差由式(35～37)定义。如图4所示,无论是s=1还是s=2,用逐点误差绝对值评估的平均轨迹误差与待定参数γ呈现了V字型的曲线。这些数值误差在γ的正半轴达到最小值。这意味着,如果通过优化γ来最小化积分的轨迹误差,算法的数值精度将得到极大的提升。然而,上述曲线中轨迹误差和能量误差曲线的最小值对应的横坐标(γ的取值)不同,因此应当考虑能量和轨迹的综合精度来确定γ的最佳值。本文以轨迹精度最佳为目标来求参数γ的最佳取值γopt。

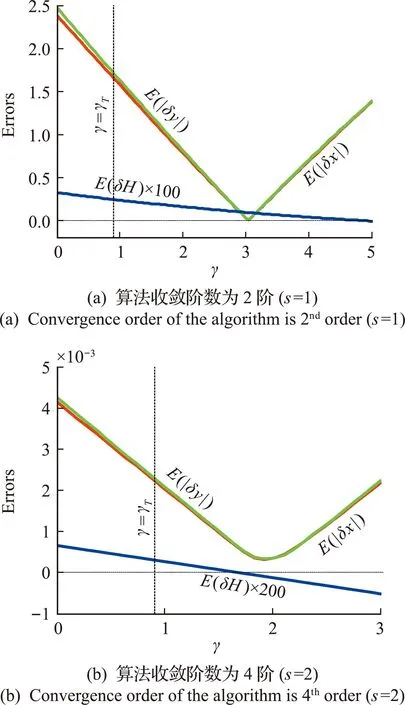
图4 数值误差随待定参数γ变化曲线

图5显示了s=1时算法数值误差随参数γ变化曲线,其中h=0.01,Nh=1000。尽管本文选择了不同的时间步长和更长的总仿真时间,但是图5与图4(a)的误差曲线是精确一致的。这意味着虽然时间步长变化了,但最优轨迹精度的参数γopt几乎不受时间步长与仿真时间长短的影响。为进一步分析轨迹误差随参数γ的变化规律,进一步定义如下均值轨迹误差

(38)

(39)

通过上述定义,轨迹的均值误差变成可正可负。图6给出了采用式(38,39)定义的误差随参数γ变化趋势,其中h=0.01,Nh=10。数值结果显示轨迹误差随参数γ呈现线性变化趋势,并且使误差最小的参数γopt与图5的值一致。因此,可以采用较少的仿真时长预估最优参数γopt。

为预估γopt的最优参数值,本文定义轨迹误差均值的和为δW=E[δx]+E[δy]。如图6所示,误差δW随参数γ呈现线性变化趋势。进一步令γ1=0,γ2=γT,δW1=δW(γ1),δW2=δW(γ2),然后将这些取值代入式(11),计算得到γopt。

图6 轨迹均值误差-γ变化曲线趋势比较

表2给出了γ1=0和γ2=γT时的误差δW1与δW2的取值,以及通过式(11)计算出的γopt取值,其中h=0.01,Nh=10。表3给出了参数γ=γopt以及h=0.04时轨迹误差。可以看出,s=1和s=2时,x方向和y方向的轨迹误差分别减小了两个和一个数量级。图7给出了s=1和h=0.04时多体平面摆x2分量与y2分量的数值结果,其中黑色线为解析解,红色○代表γ=0的数值解,蓝色×代表γ=γopt的数值解。数值结果表明,通过预先调节待定参数γ的取值,数值积分的相位误差得到了大幅降低。实际上对于s≥2的高阶情况,通过预参数调节同样可以大幅降低,本文限于篇幅略去相关讨论。需要指出,通过式(11)估计最优参数γopt需要一定的额外计算量(不随仿真时间而增长)。所以只有在长时间仿真和额外的计算量可以忽略不计时,该方法才具有较大优势。

表2 最优参数γopt计算

表3 优化精度后的数值结果

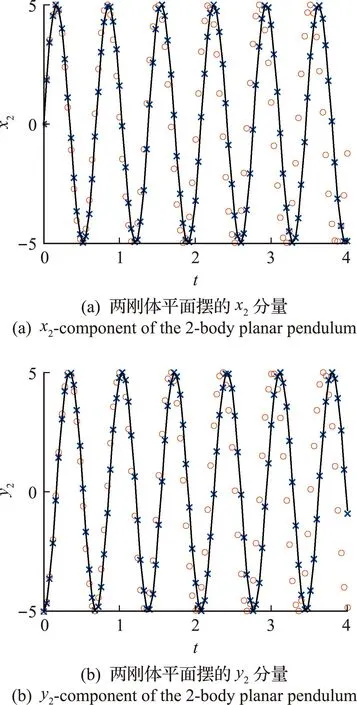
图7 两体平面摆数值结果比较

6 结 论

针对笛卡尔坐标描述的平面多刚体系统,本文提出了一种参数预调节保辛积分方法。在该方法构造过程中,首先引入约束零空间的正交投影矩阵,进而推导了平面多刚体系统的改进的拉格朗日方程,将动力学方程描述成包含待定参数γ的微分代数方程组,然后参数预调节的保辛积分方法通过离散化改进的拉格朗日方程得到。为了减小数值方法的相位误差累积,本文利用数值积分的轨迹误差与参数γ的近似线性关系,通过对误差线性插值,得到最优的参数值γopt。数值结果表明通过预先估计最优的待定参数γ,包含两个刚体平面摆的数值积分精度提升了1～2个数量级,较大幅度地减小了保辛算法随时间累积的相位误差。