精细积分方法的发展与扩展应用

姚伟岸, 高 强, 谭述君, 吴 锋

(大连理工大学 力学与航空航天学院 工业装备结构分析优化与CAE软件全国重点实验室, 大连 116024)

1 引 言

精细积分方法的基本思想由钟万勰院士1991年首次提出[1],并很快应用到结构动力初值问题的求解[2]。随后,结合计算结构力学与最优控制的模拟理论,钟万勰院士将精细积分方法的思想推广到两点边值问题[3],并持续不断推进精细积分方法的研究工作[4]。精细积分方法提出之后,经过钟万勰院士众多弟子及不同领域学术同行的不断发展,在非齐次方程精细模拟、时变动力问题、非线性动力问题、复杂大规模问题和特殊矩阵函数等基本理论和算法方面不断取得研究成果,并已经拓展应用到随机动力响应分析、热传导分析、动力弹塑性硬化和软化问题、动态载荷识别、周期结构能带分析、最优控制问题、Floquet转移矩阵计算、对称和非对称Riccati微分方程求解和Maxwell方程求解等众多领域。

精细积分方法是一种区别于传统差分类数值方法的全新的初值问题数值积分方法,其突出特色体现在:(1) 数值积分过程中,基于加法定理和2N类算法,通过仅计算和存储迭代过程中的增量,将计算过程中的截断和舍入误差降低到计算机精度之外,从而能够给出计算机浮点意义上的精确解,并能在合理积分步长范围内不发生稳定性和刚性问题; (2) 精细积分方法不仅是显式格式,并且是无条件稳定的,突破了差分类算法只有隐式格式才具有无条件稳定性的限制; (3) 精细积分方法具有零振幅衰减率、零周期扩散率和无超越性等优点。由于算法的优异性能,能够获得远优于传统差分算法的数值结果,特别是在处理刚性问题时具有差分类算法无法比拟的稳定性和精度。

本文作者在跟随钟万勰院士读博士和后期工作期间,有幸在钟先生的教诲和指导下从不同方面参与到精细积分方法的理论研究和应用工作,并不断跟踪精细积分方法的发展情况[5]。本文对精细积分方法的基本思想、深入发展和在各领域的应用做一系统综述。

2 精细积分方法的基本思想

考虑常微分方程矩阵-向量形式的一般性表达

(1)

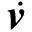
当系统矩阵A和向量f与状态v不相关时,按线性微分方程的求解理论[6],状态微分方程(1)的通解可以由状态传递矩阵和Duhamel积分表达为

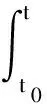
(2)

式中Φ(t,τ)为状态传递矩阵,且具有以下性质

(1)Φ(t,t)=I

(3)

(2)Φ(t,t1)=Φ(t,t2)Φ(t2,t1)

(4)

(5)

式中 用A(t)描述表明这对于时变系统也适用。

式(2)表明,状态传递矩阵Φ是求解线性微分方程的关键。对于时不变系统,A为常数矩阵时,状态传递矩阵仅与区段长度有关,即

Φ(t,t1)=Φ(t-t1)=eA(t-t1)

(6)

式中 矩阵指数

(7)

虽然从数学上,矩阵指数可采用本征向量展开方法给出,但在实际数值计算中并不是十分有效,尤其出现或接近出现Jordan型本征解时。关于矩阵指数已经提出了很多计算方法,但仍不够理想。文献[7]给出了19种可疑的算法,且25年后再予以回顾[8],指出问题并未完全解决。

2.1 精细积分方法的提出

钟万勰院士研究连续时间LQ控制本征对求解时,针对其核心问题即矩阵指数的计算,首次提出了精细积分方法[1],并达到计算机意义上的精确解。本小节综合文献[1,2,9]的论述,介绍精细积分方法的基本思想。

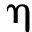
(8)

根据矩阵指数的加法定理可给出

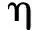
(9)

式中m=2N,而N为任意正整数,如可选N=20,则m=1048576。亦称为2N类算法。

eAτ≈I+Aτ+(Aτ)2/2+…+(Aτ)q/q!=I+Ta

(10)

式中Ta阵是一个小量的矩阵,为

Ta=Aτ+(Aτ)2/2+…+(Aτ)q/q!

(11)

计算中至关重要的一点是矩阵指数的存储只能是增量Ta,而不是(I+Ta)。因为Ta很小,当其与矩阵I相加时,就会成为其尾数,在计算机的舍入操作中,其精度将丧失殆尽。为了提高计算T阵的效率,运用2N类算法先将式(9)作分解

(12)

这种分解一直做下去,共N次。

其次应注意,对任意矩阵Tb和Tc有

(I+Tb)(I+Tc)≡I+Tb+Tc+TbTc

(13)

当Tb和Tc很小时,不应加上I之后再执行乘法。因此式(12)的N次乘法相当于

(14)

T=I+Ta

(15)

由于N次乘法后,Ta已不再是很小的矩阵,这个加法已没有严重的舍入误差。

以上是矩阵指数计算的精细积分方法的思想。文献[1]指出,精细积分有两个要点,(1) 运用矩阵指数的加法定理,即2N类算法; (2) 注意力放在增量上,而不是其全量。

2.2 基于Padé级数近似的精细积分方法

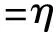
Rpq(Aτ)=[Dpq(Aτ)]-1Npq(Aτ)

(16)

式中

(17)

(18)

显然,当q=0时,Rp0(Aτ)是eAτ的p阶Taylor近似,即Taylor近似是Padé近似的特例。在实际应用中通常令p=q,即q阶对角Padé近似。下面介绍的Padé近似均表示对角Padé近似。

参照精细积分方法,将精细区段矩阵指数的q阶Padé近似的增量分离出来表示为

Rqq(Aτ)=I+Ra

(19)

同样Nqq(Aτ)和Dqq(Aτ)的增量也分离出来

Nqq(Aτ)=I+Na,Dqq(Aτ)=I+Da

(20)

式中

(21)

将式(19,20)代入式(16),可以导出

Ra=(I+Da)-1(Na-Da)

(22)

获得了Padé近似的增量部分Ra后,再采用与2.1节相同的方法,结合矩阵指数加法定理,并在执行过程中只存储和计算增量部分,就得到了基于Padé级数近似的矩阵指数精细积分方法。

由于在精细区段τ上采用了精度更高的Padé级数近似,因此在选择相同参数(N,q)的情况下,基于Padé级数近似的精细积分方法比基于Taylor级数近似的精细积分方法计算精度更高和稳定性更好。但是Padé级数增量部分Ra涉及矩阵求逆,这一定程度上影响了其计算效率,尤其是矩阵维数较大时。进一步需要指出的是,如矩阵A是Hamilton矩阵,则其对应的矩阵指数是辛矩阵。此情况可以证明基于Padé近似的精细积分方法给出的矩阵指数是辛矩阵,因此是保辛算法[11,12]。

2.3 误差分析与算法设计

无论是基于Taylor级数近似还是基于Padé级数近似的精细积分方法,其精细区段划分系数N和截断项数q的选择直接影响到矩阵指数数值逼近的精度,也直接影响到计算效率。文献[13,14]分析了基于Taylor级数逼近的精细积分方法的误差估计,并给出了(N,q)选择的经验及一些建议。文献[10]研究了当展开项数q=4时,系数N的选择,而文献[15]则分析了Hamilton矩阵指数采用一阶和二阶甚至任意阶Padé级数近似的误差估计等。上面对(N,q)的选择是在给定级数截断项数q(主要凭经验)的情况下,选择系数N以保证其计算精度,但这样得到的(N,q)组合不能保证其计算量最小。

文献[16]进一步基于误差分析理论,推导出给定精度下采用Padé级数逼近时参数(N,q)满足的条件。考虑到矩阵指数精细积分方法的计算量主要为(N+q-1)次矩阵乘法,因此可将参数(N,q)的选择描述为下面优化问题的求解

(23)

式中 EPS为指定精度

(24)

进一步,文献[16]基于该误差函数分析了N和q的增加对相对误差降低速度的影响,导出了在给定精度EPS时参数(N,q)优化组合的自适应选择算法和计算流程,此处不再赘述。

3 时不变线性微分方程的精细积分方法

许多问题的数学模型都可采用时不变线性微分方程组来描述,即在一般性描述式(1)中,A是时不变矩阵,且f与状态v不相关,表示为

(25)

(k=0,1,2,…)

(26)

在区段[tk,tk+1]上利用Duhamel积分式(2),得到时不变线性微分方程式(25)的离散递推列式为

(27)

式中

(28)

3.1 解析积分方法

钟万勰首先在文献[2]中给出了当非齐次项f在区段[tk,tk+1]为线性函数或采用线性近似时的解析积分格式。随后,林家浩等[17,18]通过引入特解vp(t)将式(27)表示为

vk+1=T[vk-vp(tk)]+vp(tk+1)

(29)

并进一步导出了在时间区段[tk,tk+1]内非齐次项f(t)为多项式、指数函数、三角函数及其组合函数时对应的特解vp(t)的解析格式,介绍如下。

(1) 当非齐次项f(t)为线性函数,即

f(t)=f0+f1·(t-tk)

(30)

其对应的特解为

vp(t)=(A-1+I·t)(-A-1f1)-A-1(f0-f1·tk)

(31)

将式(31)代入式(29),进行整理即得到如下解析积分格式

vk+1=T[vk+A-1(f0+A-1f1)]-

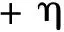
(32)

(2) 当非齐次项f(t)为三角函数,即

f(t)=f1sin(ωt)+f2cos(ωt)

(33)

其对应的特解为

vp(t)=asin(ωt)+bcos(ωt)

(34)

式中

(35)

(3) 当f(t)为多项式与三角函数的组合,即

f(t)=(f0+f1·t+f2·t2)×

[αsin(ωt)+βcos(ωt)]

(36)

其对应的特解为

vp(t)=(a0+a1·t+a2·t2)sin(ωt)+(b0+b1·t+b2·t2)cos(ωt)

(37)

式中

(i=2,1,0)

(38)

(39)

(4) 当f(t)为指数与三角函数的组合,即

f(t)=eαt[f1sin(ωt)+f2cos(ωt)]

(40)

其对应的特解为

vp(t)=eαt[asin(ωt)+bcos(ωt)]

(41)

式中

(42)

以上α,β,f0,f1,f2,a0,a1,a2,b0,b1和b2等在时间区段[tk,tk+1]内均为常量。

当非齐次项具有上述函数形式时,解析积分格式本身没有任何近似。对于一般形式的非齐次项,也可在时间区段[tk,tk+1]内用上述函数进行近似,由于递推列式简单,得到了广泛应用。

值得指出的是,上述解析积分格式中含有矩阵的逆A-1或(ω2I+A2)-1,而求逆运算容易引起数值困难,特别是当矩阵奇异或接近奇异时。对此,文献[19]指出对于奇异矩阵可先利用奇异值分解得到正交矩阵,再采用精细积分方法求解。文献[20]进一步针对奇异Hamilton系统矩阵,利用Hamilton系统的共轭辛正交归一关系将零本征值对应子空间分离出来,再采用精细积分法求解。

此外,发展避免求逆的一般性算法也得到了学者们的关注,归纳起来主要有以下三类。

3.2 直接数值积分方法

为避免矩阵求逆运算导致的数值困难,许多学者将式(27)的Duhamel积分看作普通函数的积分,记

(43)

并分别采用常用的Simpson,Romberg,Cotes和Gauss等数值积分技术进行计算,然后与矩阵指数的精细积分相结合,构造式(27)的离散递推列式。

以采用Gauss数值积分为例[21,22],式(43)的数值积分如下

(44)

式中Ng为积分点的个数,τi为Gauss积分点的坐标,wi是加权系数。将式(44)代入式(27)得到离散递推列式为

(45)

式中

(46)

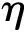
文献[23]比较了多种直接数值积分的精度,指出Cotes和Gauss积分是保持精细积分算法高精度的较好方法,文献[14,24]则进一步指出采用Padé逼近为基础的矩阵指数精细方法是无条件稳定的计算格式,可给出更高的精度。

通过直接数值积分与矩阵指数的精细积分方法相结合来构造求解列式,不需要矩阵求逆运算,也无需对非齐次项进行数学拟合,具有很好的通用性。微分方程式(27)的求解精度主要取决于Duhamel数值积分的精度。同时,式(46)表明还需计算积分点上的矩阵指数,增加了计算量。但这类方法没有充分利用Duhamel积分函数中矩阵指数的特殊性。

3.3 增维精细积分方法

文献[25]首先将增维技术应用于非齐次微分方程的精细积分求解算法的构造,指出如果非齐次项f为一组齐次线性常微分方程组的解,记为

(47)

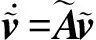
(48)

式中

(49)

增维齐次方程(48)与原非齐次方程(25)是完全等价的,可直接采用矩阵指数的精细积分方法求解。

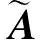
文献[26]还提出了基于Taylor级数的增维精细积分方法(也称为齐次扩容精细积分方法)。首先在时间区段[tk,tk+1]内将非齐次项f进行Taylor级数展开,即设

f(t)=fm·tm+fm-1·tm-1+…+f1·t+f0

(50)

然后引入扩展状态变量

(51)

(52)

此外,文献[29]还给出了非齐次项为正/余弦函数形式的增维方法,记非齐次项为

f(t)=acos(ωt)+bsin(ωt)

(53)

式中a和b为不依赖时间的向量。引入扩展状态变量

(54)

(55)

利用类似的思想,可以Legendre,Chebyshev,Hermite和Laguerre等正交多项式函数系[30,31]来构造增维矩阵,并且文献[31]还指出基于Legendre函数系构造齐次方程具有更高的精度和收敛性。

增维精细积分方法将非齐次方程转化为齐次方程,在实施精细积分的过程中不必进行矩阵求逆运算,同时保留了精细积分的高精度,其代价是增加了矩阵指数的计算量。

3.4 扩展精细积分方法

实际上,利用Duhamel积分中矩阵指数的特点,可以构造出与解析积分格式一样高效和精确的递推算法,而且不需要矩阵求逆运算。即文献[32]提出的扩展精细积分方法。

离散递推列式(27)表明,其关键在于第二项Duhamel积分项的计算。首先,为了充分利用非齐次项本身的特点降低计算量,将非齐次项f(t)写为

f(t)=Bfs(t)

(56)

式中 常系数矩阵B反映了非齐次项f(t)的特点,例如结构动力学方程中作动力/干扰力的位置矩阵。由于fs(t)的维数小于f(t)的维数,从而降低下面基函数响应矩阵的维数,提高计算效率。

将式(56)代入式(27),Duhamel积分项描述为

(57)

在区段[tk,tk+1]内fs(t)采用特定基函数逼近为

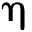
(58)

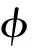
(59)

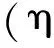
(60)

显然,基函数响应矩阵仅与矩阵A的矩阵指数、基函数和区段长度有关,体现了非齐次项在基函数模式下的响应特征。对于时不变系统,等长区段划分的基函数的响应矩阵只需计算一次。

将式(57,59)代入(27),即得到基于响应矩阵的精细积分递推公式为

(61)

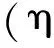
利用基函数响应矩阵表达式中含有矩阵指数的性质,文献[32]也导出了基函数为多项式函数、指数函数、正/余弦函数及其组合函数形式时响应矩阵的加法定理,同时给出了基函数响应矩阵的精细积分方法,因此称之为扩展精细积分方法。

与解析积分方法相比,扩展精细积分方法可同样给出非齐次项为多项式函数、指数函数、正/余弦函数及组合函数形式时的精确解。更具优势的是,扩展精细积分方法不需要对矩阵求逆,具有更好的数值稳定性和更广泛的适用性,对进一步构造非线性微分方程数值算法非常有意义[33,34]。

4 时变线性微分方程的精细积分方法

所谓时变线性微分方程组,就是常微分方程组的一般性描述式(1)的系统矩阵A随时间变化,记为A(t),且f与状态v不相关,表示为

(62)

此时利用状态传递矩阵和Duhamel积分表述的通解式(2)仍然成立,状态传递矩阵也仍然满足式(3～5)。在区段[tk,tk+1]上,递推式表达为

(63)

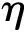
本节主要讲述以精细积分方法为基础求解齐次时变系统对应的状态传递矩阵的计算方法,而非齐次线性时变微分方程的求解与非线性微分方程的求解类似,将在下节介绍。

式(62)对应的齐次时变线性动力系统表示为

(64)

在区段[tk,tk+1]上,方程解的递推式表达为

vk+1=Φ(tk+1,tk)vk

(65)

4.1 常值近似法

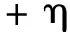
(66)

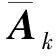
(67)

式中 定义李括号运算为

A1,A2≜A1A2-A2A1

(68)

文献[36]给出另一种4阶Magnus级数近似结果

(69)

误差理论分析表明,该方法的精度仅依赖于Magnus级数截断的阶次和区段长度。常值近似也是后面乘法摄动的基础。

4.2 乘法摄动法

时变系统虽不能完全采用精细积分方法,但可采用摄动法进行求解,并且将定常系统的精细积分作为摄动的基础。钟万勰等[37]首先提出了时变Hamilton系统的矩阵指数计算的保辛乘法摄动的思想,随后谭述君等[38]进一步将其应用于变系数Riccati方程的保辛摄动近似求解。在此基础上,富明慧等[39]将乘法摄动思想做了进一步推广,提出了一种高阶乘法摄动方法,将时变系统状态传递矩阵转换为一系列矩阵指数的乘积,并可采用精细积分方法精确计算。

对齐次时变系统(64),取区段[tk,tk+1]上的一点tc,将时变矩阵A(t)分解为定常和时变两部分,即

(70)

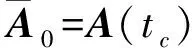
(71)

将式(71)代入式(64)可得到一阶乘法摄动系统,即

(72)

式中

(73)

这样原系统(64)就转化为一阶摄动系统(72),其系数矩阵为关于(t-tc)的一阶小量。可以看出,当tc=tk时,式(73)即为文献[38]提出的乘法摄动。

依次类推,继续进行摄动。设摄动的最终次数为M,其状态变换如下

(74)

相应的第M阶乘法摄动系统为

(75)

式中

(76)

将AM(t)分解为

(77)

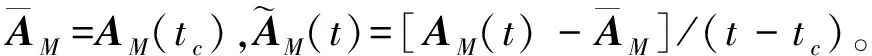
(78)

式中α=tc-tk,β=tk+1-tc

(79)

文献[39]还讨论了tc=tk,tc=tk+1和tc=(tk+tk+1)/2时Φ(tk+1,tk)的精度和计算量,指出tc=(tk+tk+1)/2时算法性价比最高。

值得指出的是,如果系统矩阵A(t)是Hamilton矩阵,那么摄动后的系统仍然是Hamilton系统,因此该方法成为一种高阶保辛摄动方法,这对于Hamilton系统求解的保辛要求是非常重要的。

4.3 周期变系数系统

周期变系数系统是一般时变线性系统的特例,即式(64)的时变系统矩阵具有周期时变特性

A(t)=A(t+T)

(80)

式中T是周期的大小。

根据Floquet-Lyapunov理论,周期时变系统的稳定性由Floquet转移矩阵特征值的实部决定。Floquet转移矩阵是状态传递矩阵在一个周期端部的值,参照式(2)的描述,记为Φ(t0+T,t0)。Floquet转移矩阵的计算,以往主要有两类方法,一类是Hsu[40]提出的一系列将矩形波方法推广于多维系统的近似方法;另一类是各种直接数值积分方法,其中,四阶预估-校正Hamming法最为有效[41]。利用系数周期性变化的特点,文献[42]将解析精细积分方法应用于Floquet转移矩阵的计算。然而该方法需要求逆运算,难以处理奇异或接近奇异矩阵情况,对此文献[43]建立了相应的扩展精细积分方法。

根据周期函数的Fourier级数展开式,式(80)描述的周期函数A(t)可采用s阶Fourier级数近似

(81)

式中ωi=i2π/T,而A0与Di,Bi(i=1,2,…,s)均为常数矩阵。将式(81)代入式(64),得到

(82)

式中

(83)

将一个周期[t0,t0+T]的时间长度均匀划分为M份,一系列等间距时刻为

(k=0,1,2,…,M)

(84)

在区段[tk,tk+1]内对v(t)采用p阶多项式近似

(85)

将式(85)代入式(83),得到

(86)

式中

(87)

在区段[tk,tk+1]上利用Duhamel积分,可以得到区段内的递推列式

(88)

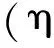
(89)

式中

(90)

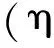
(91)

再利用传递矩阵性质式(4),即可得到周期[t0,t0+T]内任意时刻的状态传递矩阵

(k=0,1,…,M-1)

(92)

式中Φ(t0,t0)=I。

文献[43]分别给出了基于扩展精细积分的零阶格式、一阶格式和二阶格式。这些格式与同阶次的解析精细积分方法[42]相比,具有相同的精度和更高的效率,而且避免了矩阵求逆,具有更好的稳定性。该方法也用于周期时变系统H2范数的计算[44]。

4.4 多项式变系数系统

多项式变系数系统是一般时变线性系统的另一种特例,在式(64)的时变系统矩阵可以采用多项式函数描述或近似表示为

(93)

式中Ai为时不变系数矩阵。文献[45]引入新的变量和增维技术,将其转换为时不变系统的矩阵指数,再采用精细积分方法精确求解。

首先,引入变换

τ=ρ(t-t0)/(tf-t0)

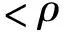
(94)

将原时变系统(64)转换为如下单位时变系统

(95)

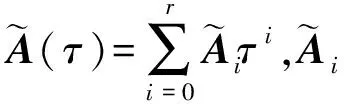
(i=1,2,…,m+r;m>r)

(96)

(97)

(98)

(99)

类似的,4.3节求解周期变系数系统状态传递矩阵的扩展精细积分方法,也可以用于本节多项式变系数系统的状态传递矩阵的计算。

5 非线性微分方程的精细积分方法

所谓非线性微分方程组,就是式(1)的右端含有状态v的非线性项。不失一般性,可以将非线性项放在系统矩阵A中,记为A(v,t),f仍然可以表示成与状态v不相关的形式表示为

(100)

式中 矩阵A(v,t)体现非线性和时变特征。显然线性时变系统是其特例,因此,下面的数值算法也适用于含非齐次项的线性时变微分方程组的求解。

5.1 基于线性系统的精细积分方法

考虑到线性微分方程求解上的优势,一个自然的想法是将非线性部分的线性部分单独提取出来,即将A(v,t)分解为

A(v,t)=A0+A1(v,t)

(101)

式中A0为定常系统矩阵,A1(v,t)表示非线性/时变部分,将其并入到非齐次项,将式(100)改写为

(102)

式中

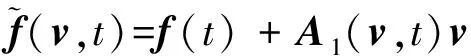
(103)

对于式(102)描述的非线性微分方程的解,在区段[tk,tk+1]内采用Duhamel积分描述的递推列式为

(104)

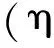
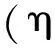
目前,对Duhamel积分中的非线性非齐次项在tk处通常采用多项式函数近似。文献[46]给出了基于一次多项式近似并结合解析积分公式导出的精细积分算法。进一步,文献[47]将其扩展到采用m次多项式近似的精细积分算法构造。

(105)

(106)

多项式函数的Duhamel积分可以给出解析表达式,其递推式如下

(107)

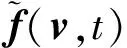
(108)

避免了解析积分格式(107)的矩阵求逆运算,但是以损失精度为代价。

实际上,第3节中面向时不变线性微分方程求解介绍的直接数值积分方法、增维精细积分方法和扩展精细积分方法等避免矩阵求逆运算的方法都可用于式(106)的求解。下面介绍文献[32,33]基于扩展精细积分和外插法构造的更为简洁的非线性微分方程的精细算法。

基于扩展精细积分方法[32],当基函数取为多项式函数时,多项式响应函数表示为

(j=0,1,…,m)

(109)

则式(106)的递推公式变为

(110)

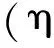
递推式(110)唯一的近似是多项式近似,其与不同数值近似方法结合将导出不同的非线性微分方程数值算法。文献[43,33]进一步导出了几种单步法/多步法的显式/隐式计算格式。以Adams线性多步法为例,如果利用tk-m,tk-m+1,…,tk-1,tk作为Lagrange插值节点,可导出基于扩展精细积分方法的显式Adams的m步法计算格式,统一描述为

(111)

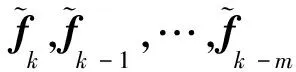
(112)

式中αj,l为显式Adams的m步法中基函数响应矩阵的组合系数,表1给出了m=1,2,3步法时的组合系数。

利用tk-m+1,…,tk-1,tk,tk+1(插值点包含未知的tk+1)作为Lagrange插值节点,可导出基于扩展精细积分方法的隐式Adams的m步法,统一描述为

(113)

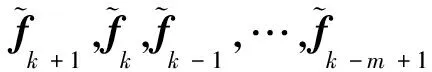
(114)

式中αj,l为隐式Adams的m步法中基函数响应矩阵的组合系数,表2给出了m=1,2,3步法时的组合系数。

表2 隐式Adams的m步法的αj,l

文献[34,49]在扩展精细积分方法基础上,将结构动力学方程中的刚度阵项看作非齐次项,改写为

(115)

(116)

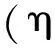
(117)

显然,利用上述结构特点和分块矩阵运算,矩阵指数和响应矩阵只有一半的元素需要计算,同时状态空间的递推式(110)也可以利用分块矩阵运算进一步简化,从而降低计算量。

文献[50]还采用四阶Runge-Kutta法来计算式(104)右端的非齐次项的Duhamel积分,而采用精细积分方法来计算齐次部分,提出了精细Runge-Kutta法的计算列式为

(118)

式中

(119)

基于式(102)的算法,A0的选择会影响到算法的精度和稳定性。然而,如何选择最优的线性系统矩阵A0,尚未找到严格的方法。文献[46]指出,为了后续算法的构造,可以通过在A0中填充元素的方式使其满秩。这似乎说明这些方法更适用于弱非线性问题,而对于强非线性问题,如何利用精细积分方法的优点还是值得研究的问题。

5.2 基于同伦摄动的精细积分方法

同伦摄动方法是近年来一种求解非线性问题的渐近数值方法,具有固定的计算格式和推导方法。文献[51]将精细积分技术和同伦摄动方法相结合,提出了基于精细积分技术的非线性动力学方程的同伦摄动法,具有较高的计算精度和效率。

针对非线性微分方程(102),构造以下线性同伦函数,即

v(t0)=v0

(120)

(121)

将式(121)代入式(120),并令方程ε同次幂的系数相等,得

(122)

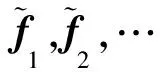
显然上述构造的同伦函数的每一个摄动方程都是时不变线性微分方程,可用第3节介绍的精细积分方法求解。得到这一组摄动解之后,代入式(121)并令ε=1,即得到原非线性微分方程的解答。

5.3 增维为齐次时变系统的方法

(123)

则非线性微分方程(100)转化为齐次方程形式,即

(124)

文献[53]提出了一种在Minkowski空间中齐次化非线性系统的增维方法。对一般非线性系统

(125)

(126)

式中

(127)

(128)

式中G为一个Minkowski矩阵

(129)

这样,原非线性动态系统就转化为一个增维的Lie型动态系统,可采用精细积分方法求解。文献[54]则进一步采用Runge-Kutta Munthe-Kaas方法和精细积分方法构造了简洁的保群结构积分算法。

6 大规模问题的精细积分方法

大规模工程问题的瞬态响应分析,其相应的系数矩阵通常具有很高的维度,若直接采用精细积分方法进行计算,需要计算高维度矩阵的相乘并破坏原始系数矩阵的稀疏性,从而导致消耗大量的计算时间和储存空间。

6.1 子域精细积分法

为降低精细积分方法的计算量,钟万勰等[55-57]提出了子域精细积分方法。主要思想是利用系数矩阵具有窄带宽的特点将结构分为若干个子域,将计算转化为一些子域上的精细积分计算。在此基础上,陈飙松等[58]提出了子结构精细积分方法,该方法将物理域划分子结构,更适合于有限元法及并行计算。考虑瞬态热传导问题的一阶常微分方程组

(130)

式中C和K分别为热容矩阵和热传导矩阵,T和F分别为节点温度和热载荷向量。假设结构可以分为A和B两个子结构,则式(130)可改写为

(131)

令

(132)

则式(131)可以进一步改写为

(133)

根据精细积分方法,式(133)的解可以表示为

(134)

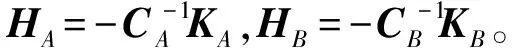
在时间段[tk,tk+1]内,做如下近似

(p=A,B)

(135)

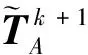
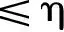
(136)

子域精细积分方法提出后,针对子域精细积分方法的改进和应用做了大量工作。蔡志勤等[59]对子域精细积分方法的稳定性进行了分析,证明了单点、两点和三点子域精细积分及单点子域精细积分的蛙跳格式都是无条件稳定的。曾文平[60,61]分别对二维和三维扩散方程提出了单点子域精细积分方法。金承日等[62,63]利用子域精细积分方法思想,针对对流方程初边值问题,构造出一组无条件稳定的三层显格式(蛙跳格式)和一组无条件稳定的二层隐式格式,进而设计出求解该隐式格式的显式迭代算法。赖永星等[64]基于单点子域精细积分思想,针对抛物线型热传导方程初边值问题,提出多点子域积分的概念,推出一种多点子域积分的FTCS(Forward for Time,Center for Space)格式,并且说明了多点子域积分的FTCS格式具有比单点子域积分的FTCS格式收敛速度快的特点。Wu等[65]针对由相同结构单元组成的周期结构动力响应问题,基于精细积分方法、子域格式和周期结构的可重复性提出了一种子域精细积分方法,此方法特别适用于周期结构动力响应的求解。

6.2 Krylov子空间精细积分方法

Fung等[66]首先将Krylov子空间方法和精细积分方法相结合,提出了一种求解大规模瞬态问题的高效精细积分算法。对一个给定的n维方阵A以及非零向量v,定义m维Krylov子空间为

Km≡span{v,Av,A2v,…,Am-1v}

(137)

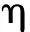
(1) 初始化

β=‖v‖2,v1=v/β

(138)

(2) 迭代过程

Doj=1,2,…,m-1

①w=Avj

② Doi=1,2,…,j

hi,j=wTvi

w=w-hi,jvi

③hj+1,i=‖w‖2,vj+1=w/hj+1,i

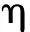
(139)

式中 向量e1的第一个元素为1,其余元素均为0。

在此基础上,陈臻林[67]提出了一种结合Krylov子空间方法的精细时程积分法求解大型动力系统,该方法利用增维技术避免了非齐次方程特解的求解,可处理任意形式载荷。Wang[68]在利用分段插值多项式模拟外载荷基础上,提出了一种使用Ritz矢量的精细积分方法和一种改进的Krylov精细积分方法。Chen[69]针对具有任意激励的二阶微分方程,提出了一种改进的Krylov精细积分算法,该方法通过精确确定迭代子空间大小以解决复杂激励问题。

6.3 基于物理特性的快速精细积分方法

高强等[70,71]根据结构动力响应的物理特点,从物理上说明了大规模动力系统对应的小时间段矩阵指数应该具有稀疏性,并基于该性质提出了一种改进的快速精细积分方法。

空间离散后的结构动力学方程为

(140)

式(140)可以写为状态空间形式,即

(141)

其中

(142)

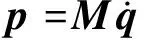
(143)

式中

(144)

离散结构动力学响应的传递速度是有限的,下面利用这个性质说明其对矩阵指数结构的影响。根据式(143),如果外力为零,则式(143)可以改写为

qk+1=T11qk+T12pk,pk+1=T21qk+T22pk

(145)

假设某个自由度上有扰动,在较小时间内必然只能传播到有限的自由度,而不是所有自由度。根据矩阵T11,T12,T21和T22的物理含义,则其一定是稀疏矩阵。基于以上分析,该方法对精细积分方法计算过程进行稀疏化过滤处理,即在循环计算矩阵指数T的增量部分时,在每一循环结束前都对矩阵指数内由于计算误差产生的小于容差的数进行过滤(即其值设为0),来提高矩阵指数的稀疏性,从而提高计算效率。根据类似思想,吴锋等[72]针对双曲热传导问题的物理特点,提出了一种求解大规模双曲热传导问题的快速精细积分方法。

6.4 基于切比雪夫展开的高效率精细积分方法

考虑如下一类特殊形式的一阶常微分方程组

(146)

式中 矩阵C为对称正定稀疏矩阵,矩阵K为对称半正定稀疏矩阵。如有限元离散化后的瞬态热传导问题的一阶常微分方程组即满足式(146)。

针对于这类特殊的常微分方程组问题,高强等[73]提出了切比雪夫展开高效数值方法。该方法基于矩阵指数的切比雪夫矩阵多项式展开,将矩阵指数-向量的乘积转化为计算一系列切比雪夫矩阵多项式与向量的乘积,从而显著提高了计算效率。

对矩阵C进行Cholesky分解C=LLT,则式(146)可改写为

(147)

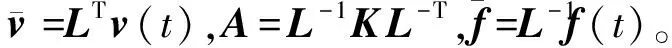
(148)

然后采用以下切比雪夫展开法计算式(148)的矩阵指数-向量乘积

(149)

式中

(150)

Anorm=(2A-λmaxI)/λmax

(151)

式中δn,0满足当n=0时δn,0=1,而当n>0时δn,0=0;λmax为矩阵A的最大特征值;In(x)为n阶第一类修正贝塞尔函数;Tn(X)为n阶第一类切比雪夫矩阵多项式,可按以下递归过程计算

(152)

(153)

式中

(154)

由式(154)可知,由于向量un和n有关,计算式(153)右端级数的每一项都需要计算一次向量积分,根据实际问题中外载荷随时间变化特点,文献[73]给出了高效计算式(153)的方法。

稳定性分析表明,对于任意时间步长,该方法近似算子的谱半径均小于1,因此该方法具有无条件稳定的特性。同时,其计算过程中只涉及矩阵-向量乘积计算并只需储存少数向量,因此针对大规模瞬态热传导问题,该方法在计算效率和内存消耗上都具有很大的优势。

6.5 周期结构的高效率精细积分方法

基于周期结构动力响应的物理特点,高强等[74-76]提出了周期结构动力响应分析的高效率精细积分方法。

假设周期结构的一个单胞自由度数为d,并将矩阵指数T按照方程(144)分块,则周期结构对应的矩阵指数具有以下特点

(155)

由式(155)可知,周期结构对应的矩阵指数中有很多相同的矩阵元素,为提高计算效率,这些相同的元素不应该全部计算和存储。另一个影响因素是能量在结构中的传递速度是有限的。假设某个自由度上有扰动,在较小步长内,必然只能传播到有限的自由度,而不可能传播到所有自由度。

综合以上两个性质,则矩阵块T11,T12,T21和T22都具有如下的带状结构,即

[]

(156)

式中 标量ai(i=1,2,…,d)对应于矩阵的对角线元素,向量bi(i=1,2,…,d)的第一个元素不为零,而向量ci(i=1,2,…,d)的最后一个元素不为零。因此,要计算周期结构矩阵指数,只需要计算和存储ai,bi和ci(i=1,2,…,d)即可。

下面以图1(a)所示的含有N个单胞的一维周期结构来说明ai,bi和ci(i=1,2,…,d)的计算方法。假设在一个积分步长内,能量传播的速度不超过m个单胞,则可构造如图1(b)所示的由2m+1个单胞组成的代表单胞结构。这两个结构的边界都不会对第m+1个单胞上的位移和动量响应产生影响,所以两个结构对应节点的响应相同,而结构(a)中第2m+2到第N个单胞对应的响应为零。

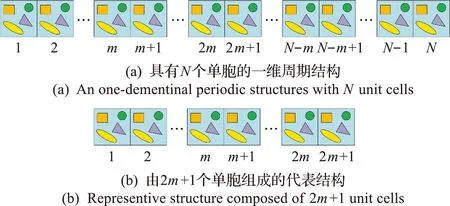
图1

因此,基于以上周期结构动力响应矩阵指数的代数结构分析,计算结构(b)的矩阵指数,并从恰当的位置提取数据即可得到式(156)的ai,bi和ci(i=1,2,…,d)。从而大大降低了矩阵指数的计算量和储存量。

基于类似思想,高强等[77,78]提出了求解一维和二维周期结构瞬态热传导问题的高效率数值方法。在此基础上,高强等[79,80]针对含有移动热源的周期结构和缺陷周期结构瞬态热传导问题提出了高效数值方法。

7 精细积分思想的扩展应用

精细积分方法的要点在于2N类算法和增量存储。基于这两个要点,精细积分方法也扩展用于许多其他问题,解决了传统方法在计算这些问题时精度低的困境。

7.1 两点边值问题

基于计算结构力学和最优控制之间的模拟理论,钟万勰等[3,81,82]进一步将精细积分方法扩展至两点边值问题。

设整个两端边值问题的求解域为[za,zb],两端边值问题的一阶2n维齐次方程可描述为

dv/dz=Av,v=[qT,pT]T

(157)

式中A为2n维的系统矩阵,v为2n维的待求状态向量。在边界za和zb处各有n个已知量,不失一般性,本文设为qa=q(za)和pb=p(zb)。对于两端边值问题精细积分法虽然不能直接使用,但是其增量存储和基于加法定理的2N类算法的思想仍然适用。式(157)通常可以采用矩阵指数方法或区段混合能方法进行求解。

(1) 矩阵指数方法

设两端边值问题的求解域为[za,zb],即求解域长度为L=zb-za,则方程(157)的解可表示为

(158)

式中Φ(L)=eAL可采用精细积分求解。将Φ(L)写成分块矩阵形式,则有

(159)

式(159)将两端的状态向量联系起来。由于已知qa和pb,则重新整理式(159)可得

(160)

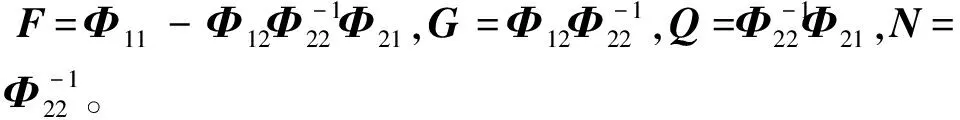
(2) 区段混合能方法

区段混合能方法常用于最优控制[84],钟万勰[83]提出了用区段混合能求解非对称Riccati方程的方法,这一方法也可用到求解两端边值问题(157)。

考虑到力学问题中,A为Hamilton矩阵的情况比较常见,本文以Hamilton矩阵为例进行介绍。将式(157)写成分块矩阵形式,即

(161)

式中B和D为对称矩阵。此时式(160)具有如下形式

(162)

式中F,G和Q是区段长度L=zb-za的矩阵函数。参考精细积分方法的思想,首先将求解区域等分为2N个小区段,在每个小区段τ=2-NL上,F,G和Q可用M项Taylor级数近似展开为

(163)

式中θk,γk和φk为Taylor展开的系数矩阵

θ1=B,γ1=D,φ1=C

(164)

而k=2,3,…,M时

(165)

同时,还存在增量加法定理

(166)

两点边值问题的精细积分方法提出后,首先在LQ控制[89,90]、Riccati方程[82]、卡尔曼-布西滤波[91]和H∞控制系统[92,93]等方面得到广泛应用,文献[84,94]等对这些应用作了详细介绍。两点边值问题的精细积分方法还广泛用于波传播问题[95-100]、分层地基动力响应问题[101,102]、电磁波反射和投射问题[103]和奇异摄动边值问题[104,105]等方面。

7.2 椭圆函数

椭圆函数是由椭圆积分定义的一类函数,广泛应用于工程问题。椭圆函数的直接计算一般比较困难,但可进行幂级数展开,且也有加法定理的重要性质,因此可采用精细积分方法思想进行求解[106]。

以Jacobi椭圆函数为例,介绍椭圆函数的精细积分方法。Jacobi椭圆函数的定义可从第二类Legendre椭圆积分引出,该积分为

(167)

式中 参数m0称为模数。Jacobi椭圆函数sn(u,m0)=z定义为上述第二类Legendre椭圆积分的反函数。而另外两个基本Jacobi椭圆函数可分别定义为

(168)

式中 省略了参数m0,这是文献常用写法。

这三个Jacobi椭圆函数有如下的幂级数展开

(169)

和如下加法定理

(170)

如果计算Jacobi椭圆函数在u点的值,可令τ=u/2N,此时τ将为非常小的数值,采用较少项数的幂级数展开即可较为精确地近似

(171)

再根据式(170,171)可得

(172)

利用式(172)迭代N次,可以得到

sn(u)=SN, cn(u)=1+CN, dn(u)=1+DN

(173)

实际的数值实验表明,精细积分方法对于m0取任意值均可给出极高精度的计算结果。目前,椭圆函数的精细积分方法已成功应用在海床动态响应[107]、Schwarz-Christoffel变换模型求解[108]和浅水波方程求解[109]等问题上。

7.3 矩阵正/余弦

矩阵正/余弦也是工程中经常用到的一种矩阵函数。对于较小规模问题,一般可以采用Jordan标准型及级数展开法精确地求解。但当矩阵维度较大时,Jordan方法并不合适。精细积分法也可用于矩阵正/余弦的计算,并具有十分出色的表现[110]。

取适当的正整数N,则矩阵A的正/余弦化为

sinA=sin(2NB), cosA=cos(2NB)

(174)

式中B=A/2N。记

sin(2iB)=Si, cos(2iB)=I+Ci

(175)

因B的数值非常小,因此根据Taylor级数展开有

sinB≈B-B3/3!+B5/5!=S0

cosB≈I-B2/2!+B4/4!=I+C0

(176)

式中I为单位矩阵。然后利用矩阵正/余弦的2倍角公式,可得到如下的递推关系

(177)

通过式(177)对增量进行N次的计算后,最终可获得

sinA=SN, cosA=I+CN

(178)

此时计算得到的增量CN已经不再是一个很小的量,当其与单位矩阵相加时,计算机的舍入误差已经可以忽略不计,能够保证计算的精度。

矩阵正/余弦的精细积分方法无需计算矩阵的特征值和特征向量,而且对实复数矩阵均适用,并可以给出计算机意义上的精确解,非常适合大规模矩阵的计算。

7.4 分数阶微分方程

一些复杂力学物理过程往往具有明显的记忆、遗传和路径依赖性质[111],由于分数阶微积分具有良好的时间记忆性[112],已经广泛应用于这些复杂力学物理过程中[113,114]。然而,求解分数阶微分方程十分困难,常用的方法包括多项式法[115,116]、模型降阶法[117]和龙格-库塔法[118]等,但这些方法的精度均不够理想。众多学者也尝试将精细积分方法用于分数阶微分方程,以期提高求解精度。一类是将分数阶微分动力方程近似转化为整数阶微分方程,之后再利用精细积分方法求解对应的近似整数阶微分方程[119,120];另一类是直接对分数阶微分方程构建精细积分方法[121]。本节对第二类研究进行介绍。

分数阶常微分方程的一般形式为

D(α)x(t)=Ax(t)

(0<α<1)

(179)

式中x(t)=[x1(t),x2(t),…,xn(t)]T,D为导数算子,A∈Rn×n。

利用拉氏变换及逆变换可得到式(179)的解为

x(t)=Eα,1(Atα)x(0)

(180)

式中Eα,β(X)为双变量Mittag-Leffler函数(简称ML函数)

(181)

式中α和β为两个变量,Γ(·)表示伽马函数。记

(182)

式中

ak=1/Γ(1+kα)

(k=0,1,2,…)

(183)

(184)

于是有

(185)

式中

(186)

显然ML函数不满足加法定理,因此建立F(2X)和F(X)的关系时,需要引入修正项R(X)。记

(187)

将式(184,186)代入式(187)即可给出修正项函数R(X),显然其可以表示为

(188)

式中 系数bk可用ak(k=2,3,…,∞)表示。实际数值计算时,函数R(X)的表达式可近似地取为有限项。当Q1和Q2的多项式定义式分别截取m1和m2项,所得函数R(X)的多项式次数为max(m2,2m1),为提高精度,一般取m2≥m1。

于是可得到如下递推关系式(i=1,2,…)

F(2iX)=I+Qi+1(2iX)

(189)

(190)

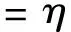
F(Aτ)=I+Q1(Aτ)

(191)

Q1(Aτ)≈Aτ/Γ(1+α)+(Aτ)2/Γ(1+2α)+(Aτ)3/Γ(1+3α)+…+(Aτ)s/Γ(1+sα)

(192)

式中s为整数,类比精细积分方法,可取s=[4/α],[·]表示Gauss函数,Q1是一个小量矩阵。

然后应用递推关系式(189,190),最终可得到ML方程(181)的精细积分方法的求解表达式,即

(193)

再结合式(180,193)即可解分数阶常微分方程(179)。

由于分数阶常微分方程解析解中的ML函数与常规的矩阵指数不同,不满足加法定理,因此分数阶微分方程的精细积分方法需要在迭代关系中加入修正项,同时因为修正项的存在,导致分数阶微分方程的计算量增加,其计算量为普通整数阶精细积分方法的p倍,其中p为多项式R(X)的次数。

7.5 病态代数方程

富明慧等[122]将病态代数方程归结于一个常微分方程初值问题的极限形式,并结合精细积分方法,提出了一种基于精细积分思想的求解病态方程组的高效方法。

对于正定的系数矩阵A,由于

(194)

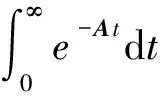
定义函数

(195)

因为

[I+e-Aτ]F(τ)

(196)

重复上述过程k次,可得

(197)

由方程(197)可知,随着迭代次数的不断增加,积分的上限以指数形式增加,因此该迭代方程可以高效地逼近逆阵A-1。实际计算时,迭代的初始值τ取为一非常小的数值,则F(τ)可用Taylor展开的前几项近似计算,如可取

F(τ)≈Iτ-Aτ2/2+A2τ3/6-A3τ4/24

(198)

同时e-Aτ也只保留Taylor展开前几项进行近似计算

e-Aτ≈I-Aτ+(Aτ)2/2-(Aτ)3/6=I+T0

(199)

将式(198,199)代入式(197),并注意对s=1,2,…有如下迭代格式,

(200)

即可得到病态系数矩阵A的逆A-1的高精度解。

理论上,随着迭代次数的不断增加,精细积分法的结果应该不断逼近理论解。然而矩阵乘积引起的计算误差会随着迭代的进行而积累,进而导致精度迅速下降甚至出现溢出。为此,富明慧等[123]针对该问题提出了相应的迭代收敛准则。郝强等[124]引入了主元加权的思想,提高了精细积分的计算精度。王慧蓉等[125]将病态系数矩阵A进行分裂,以减小病态系数矩阵的条件数。此后,一些学者又对病态代数方程的精细积分方法的计算效率进行了一定程度的优化,如张文志等[126]改进了迭代的格式,进一步降低了采用精细积分方法求解病态代数方程的计算量;富明慧等[127]利用范数均衡预处理法对病态系数矩阵A进行预处理,提升了精细积分方法计算效率。

8 结 论

矩阵指数的精细积分方法可以给出计算机意义上的精确解,得益于2N类算法和增量存储两个核心要点。2N类算法使得精细划分和高效计算成为可能,而增量存储则保证在执行2N类算法的合并过程中避免计算机舍入误差成为影响精度的主要因素,这也是矩阵指数精细积分方法成功的关键。

矩阵指数在微分方程的求解中具有重要的地位,因此在矩阵指数的精细积分方法取得成功之后,迅速用于线性/非线性微分方程数值算法的构造,得到了一系列基于精细积分的高精度、高稳定性数值算法,极大地丰富了微分方程的数值计算方法。同时,精细积分方法的思想也扩展应用于很多其他问题,包括两点边值问题、椭圆函数、矩阵正/余弦函数、病态代数方程以及分数阶微分方程等问题高精度求解算法的构造中。这些已有工作很好展现出精细积分方法的特色和优势。

进一步,精细积分方法可望在下面几个方向得到发展和突破。 (1) 保辛数值离散已成为Hamilton动力系统数值算法设计的重要原则,结合精细积分方法,可望设计出性能更高的保辛算法。 (2) 精细积分方法在弱非线性问题求解中表现出了优异的性能,如何将精细积分方法应用于强非线性问题,并构造高性能的求解算法是一个挑战。 (3) 复杂大规模问题的高效分析是解决工程问题的关键,在保证精细积分方法精度优势的同时提高计算效率是一个值得关注的问题。

致谢：谨以此文纪念钟万勰先生九十诞辰!