一种Birkhoff形式下结构动响应问题的保辛中点格式

邱志平, 邱 宇

(1.北京航空航天大学 航空科学与工程学院,北京 100191;2.北京航空航天大学 沈元学院,北京 100191)

1 引 言

结构动响应预测是工程中非常重要的问题,同时是结构振动控制和载荷识别的基础[1]。结构动响应预测主要依靠的是动力学分析的相关方法,而传统的结构动力学分析主要基于Lagrange体系,以变分原理为基石[2],且基于此已经发展出了成熟且应用广泛的分析方法。Hamilton对经典力学重新表述并基于此建立了Hamilton力学体系,相较于Lagrange体系其具有明显的辛结构[3]但是不具有对应的变分原理。由Birkhoff[4]提出的Birkhoff系统是Hamilton系统最自然的一般推广,同时拥有辛结构和相应的变分原理[5]。其考虑耗散项,相比Hamilton系统能够涵盖更多的实际力学系统。因此,利用Birkhoff系统的相关方法和原理求解结构动响应问题具有重要的意义。

目前,Birkhoff方程的求解方法大多从Hamilton算法[6-9]推广而来。张兴武等[10]将哈密顿辛差分格式推广至自治Birkhoff系统,利用Cayley变换构造了自治Birkhoff系统的欧拉中点等辛差分格式。基于哈密顿系统的生成函数法,苏红玲等[11]提出了构造Birkhoff系统辛算法的生成函数法。近年来,文献[12-14]基于Paff-Birkhoff变分原理,通过离散方法直接获得了约束Birkhoff系统等的Birkhoff辛算法。

然而,以上方法仍然存在局限性。自治Birkhoff系统的欧拉中点格式要求反对称系数矩阵非奇异,因而无法适用于奇数维广义Birkhoff系统。生成函数法存在构造的困难,实际应用存在障碍。离散的Birkhoff方法存在离散误差,使得解存在波动性。

本文针对结构动响应问题,提出一种Birkhoff形式下的保辛中点格式。首先将保守和非保守情形下的结构动响应方程化为线性自治的Birkhoff方程。之后对该线性自治方程进行中心差分,经过推导得到其中点格式。该中点格式不需要对Birkhoff方程中的反对称矩阵求逆,从而不要求该矩阵非奇异,因此适用于奇数维广义Birkhoff系统。最后通过两个数值算例说明了本文方法的有效性。

2 Birkhoff方程及其辛结构

Birkhoff方程是哈密顿方程的自然推广,其一般形式为[14]

(1)

式中z=(z1,z2,…,zm)T∈m,m可以是偶数,也可以是奇数。当m为奇数时,式(1)称为奇数维Birkhoff方程[16]。式(1)中B(z,t)和F(z,t)统称为Birkhoff函数,特别称B(z,t)为Birkhoff量。K为一个反对称矩阵,其元素满足

(2)

当Birkhoff函数B和F都不显含时间变量t时,称Birkhoff方程(1)为自治的,其形式为

(3)

当Birkhoff函数F不显含时间t,而B显含时间t时,称Birkhoff方程(1)为半自治的,其形式为

(4)

当Birkhoff函数B和F都显含时间t时,此时称为非自治的,即为式(1)的形式。

对于自治Birkhoff方程(3),当系数矩阵K为常数矩阵,且Birkhoff函数B为变量z的二次型,即

(5)

称方程(3)为线性自治Birkhoff方程,其中G为对称的常数矩阵。线性自治Birkhoff方程的形式可以表示为

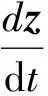
(6)

由Kij可以定义一个2-形式,用局部坐标表示为

(7)

闭2-形式(7)包括了自治和半自治Birkhoff方程的几何结构[14]。

3 结构动响应问题的线性自治Birkhoff形式

结构动响应问题的控制方程可以表示为

(8)

式中M为质量矩阵,D为阻尼矩阵,S为刚度矩阵,其都是对称矩阵。

首先考虑保守情况,即D=0,且不存在外激励载荷F(t)。此时动响应方程的形式为

(9)

(10)

将其系数矩阵记为A和C,那么方程(10)化为

(11)

显然其是线性自治Birkhoff方程的形式。

(12)

将其系数矩阵分别记为A,B和N,方程(12)化为

(13)

注意其中A为反对称矩阵。

利用摄动方法[17],可将方程(13)化为一系列线性自治Birkhoff方程[17]。引入小参数ε,将矩阵B表示为

B=B0+εB1

(14)

式中B0=(BT+B)/2,B1=(BT-B)/2。将自变量z表示为摄动级数展开形式

z=z0+z1ε+z2ε2+…

(15)

将式(14,15)代入式(13)可得一系列摄动方程

(16)

对于0阶摄动方程,可以转化为一个线性自治Birkhoff方程

(17)

同样地,可以将剩余的摄动方程通过变量变换的形式化为一系列线性自治Birkhoff方程,即

(18)

4 线性自治Birkhoff方程的中点格式

对于形如式(6)的线性自治Birkhoff方程,对其进行中心差分,可得

K(zk+1-zk)/τ=G(zk+1+zk)

(19)

式中τ为时间步长,zk和zk+1为第k和k+1个时间步z的值。对式(19)整理可得

(20)

那么步进映射zkzk+1的Jacobi矩阵为

(21)

对于矩阵P=G-1K,显然有

KP+PTK=KG-1K+KTG-TK=

KG-1K-KG-1K=0

(22)

因此P为无穷小辛矩阵,同理乘上常数系数后2G-1K/τ仍为无穷小辛矩阵,而Φτ为无穷小辛矩阵2G-1K/τ的Cayley变换[10]。于是有

(23)

线性自治Birkhoff方程的辛结构为式(7)的形式,其矩阵形式为

(24)

对于离散的线性自治Birkhoff方程,第k和k+1两个时间步的辛结构之差为

(25)

将式(21)代入式(25),并利用关系式(23),可得

(26)

因此,本文提出的中点格式(20)是保辛的。

5 数值算例

5.1 三自由度弹簧质点系统

首先将本文方法应用于一个三自由度的弹簧质点系统,其是一个保守系统,如图1所示。

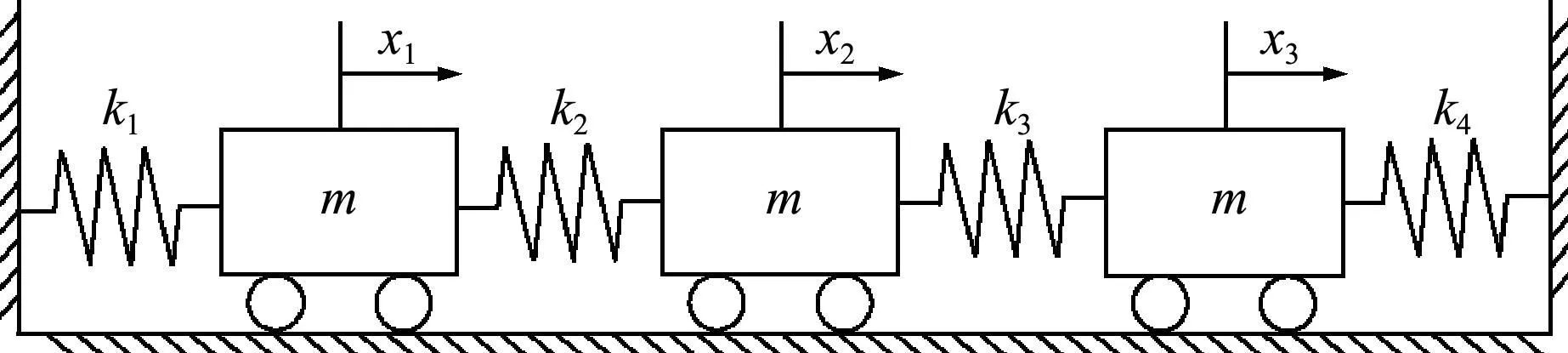
图1 三自由度弹簧质点系统

每个质量块的质量均为m=1 kg,而弹簧的刚度系数具有较大的分散性,用以验证算法的稳定性,其分别为k1=1000 N/m,k2=100 N/m,k3=10 N/m,k4=1 N/m。该系统运动方程的矩阵形式为

(27)

式中x=(x1,x2,x3)T,质量矩阵M和刚度矩阵S分别为

(28)

将初始条件设置为

(29)

对于式(27)的保守系统,可以直接引入新变量化为线性子自治Birkhoff方程。令

(30)

那么方程形式为

(31)

式中A为反对称矩阵,其形式为

(32)

B为对称矩阵,其具体形式为

(33)

首先检验算法在大步长下的表现,取步长为0.1 s,仿真时间为2 s,对比不同算法在x1位移求解的表现。x1位移解析解表达式为

x1(t)=-0.0990cos(ω1t)+0.0979cos(ω2t)+0.0011cos(ω3t)

(34)

(35)

在此步长下,四阶龙格库塔方法很快就发散了,如图2所示。而本文所提保辛中点格式与解析解吻合良好,如图3所示。这说明了本文的保辛中点格式具有良好的稳定性,即便在大步长下求解大刚度差异系统响应,仍能保持高精度。

进一步检验算法在长时间计算下的表现,仍取步长为0.1 s,取仿真时间为20 s。本文的保辛中点格式的结果与解析解的对比如图4所示。可以看出,在长时间计算下,本文的保辛中点格式仍与解析解保持一致,这说明了算法的高精度。

图2 四阶龙格库塔方法与解析解对比

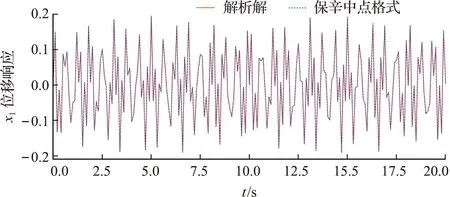
图4 长时间计算下本文的保辛中点格式与解析解对比

5.2 两室建筑振动问题

一些大型建筑,如机场航站楼和大型仓库等,在研究这些建筑的内部压力时,可以将其简化为具有开口的两室建筑。下面考虑这样一个两室建筑,如图5所示,其是一个非保守系统。

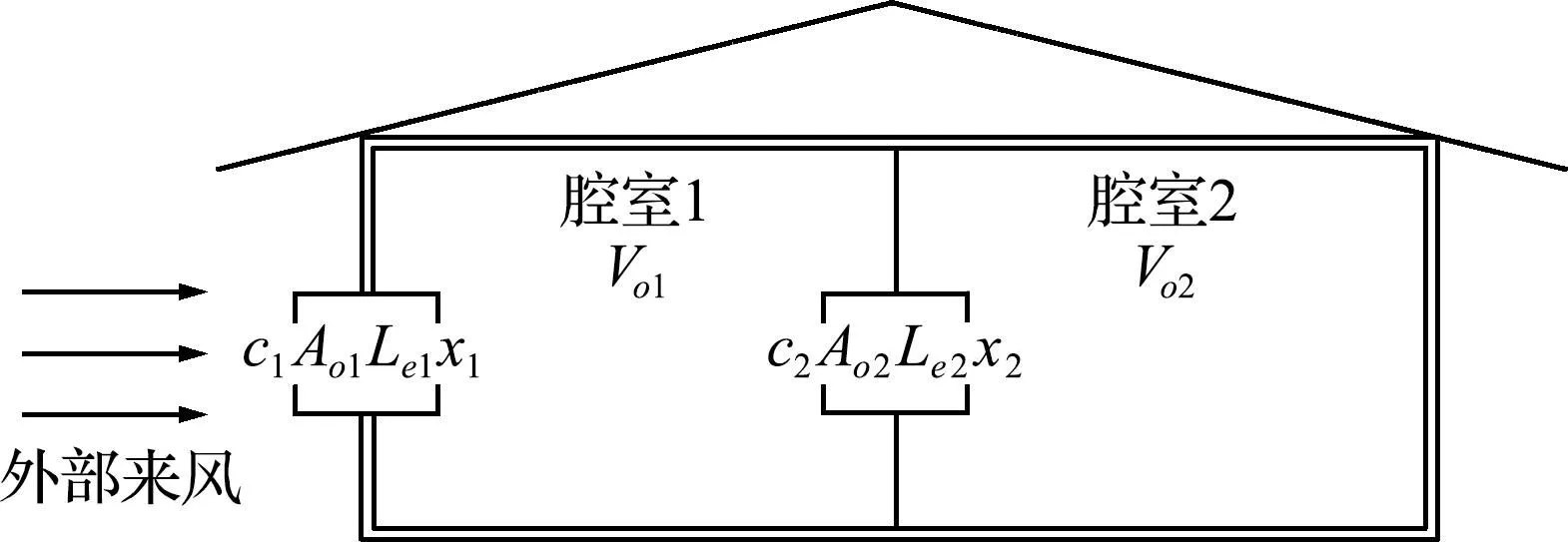
图5 两室建筑

该系统运动方程的矩阵形式为

(36)

式中

(37)

(38)

各个参数的取值列入表1[19]。

采用本文保辛中点格式求解,并与四阶龙格库塔方法比较,取时间步长为0.2 s,仿真时间为2 s。取四阶龙格库塔方法在2×10-4s步长下的结果作为参考解,对比算法的精度,如图6所示。可以看出,对于非保守系统,本文的保辛中点格式仍具有高精度。

表1 两室建筑参数取值

图6 本文的保辛中点格式与四阶龙格库塔和参考解的比较

6 结 论

针对结构动响应问题,本文提出了一种Birkhoff形式下的保辛中点格式。这种方法相较于传统方法,具有精度高和稳定性强的特点。相较于其他隐式的保辛离散方法,本文的显式方法需要更少的迭代步骤和计算资源,因此在实际应用中具有更高的求解效率。此外,由于算法中无需对反对称系数矩阵求逆,因此也适用于奇数维Birkhoff方程。两个数值算例表明了算法的有效性,相比于四阶龙格库塔更具有优势。

需要注意的是,本文方法是在线性Birkhoff 系统的框架内提出的。对于非线性系统,由于其非线性系数矩阵的存在,本文方法无法直接应用。然而借助一些变换方法(如摄动法等),存在将本文方法应用于非线性Birkhoff系统的可能性。