Analyzing wrinkling instabilities in constrained dielectric elastomers：A symplectic eigenvalue approach

ZHANG Teng

(Department of Mechanical and Aerospace Engineering,Syracuse University,NY 13244,USA)

Abstract： Symplectic elasticity has been widely used to find the exact solutions of various boundary value problems in elasticity,compute the surface wave modes,and predict surface wrinkles in multilayer hyper-elastic films.Here,we show that the symplectic analysis framework can also be applied to surface wrinkles in constrained dielectric elastomers,where the mechanical deformation is tightly coupled with the electric field.The critical voltage for wrinkles can be solved as a symplectic eigenvalue problem after introducing the dual variables to the primary variables of mechanical and electric displacement vectors.We employ the extended Wittrick-Williams (W-W) algorithm and precise integration method to solve the eigenvalues of the formulated symplectic eigenvalue problem accurately and efficiently.The symplectic analysis is validated by comparing the wrinkle voltage and wavenumber with benchmark results of wrinkles with and without surface energy.The symplectic framework is concise and applicable to other instability problems such as layered dielectric elastomers,magnetoelastic instabilities and the micro- and macro-instabilities of laminated composite structures.

Key words： symplectic;dielectric elastomers;wrinkling;eigenvalue analysis

1 Introduction

Symplectic elasticity,pioneered by Prof.Zhonget al.[1-4],represents a theorical framework of transferring elliptic partial differential equations into Hamiltonian systems of first ordinary differential equations via mimicking the time coordinate with one spatial coordinate.Over the past three decades,symplectic analysis has significantly advanced the analysis of various complex problems,from solving boundary value problems in elasticity[4-7]and plates[8-11]to understanding the wave propagation in layered materials[12-15]and predicting surface wrinkles in multilayer hyper-elastic films[16,17].Recent efforts have been devoted to extending the analysis beyond purely mechanical systems by incorporating multphysics couplings,such as guided waves in magneto-electro-elastic laminated structures[18].

The analysis becomes even more challenging when themultiphysics interactions are coupled with large deformation.Examples include surface wrinkles and creases in a constrained dielectric elastomer layer[19-23],where the voltage difference between the top and bottom surface and the mechanical confinement create driving force for the surface instabilities.The instability induced surface patterns can dynamically change the surface topography and generate new functions,such as on-demand fluorescent patterning[24].The surface instabilities,including the critical wrinkling voltage and wrinkling wavelength have also been shown modulated by surface energy[23,25,26],an important factor for very soft materials.The rich deformation patterns and promising applications have attracted numerous theoretical attentions to investigate the surface instabilities in the dielectric elastomers[25-29].

Here,we will show that the analysis of surface wrinkling in constrained dielectricelastoemers can be formulated as a symplectic eigenvalue problem,which can be accurately and efficiently solved by leveraging the powerful tool developed in the literature.The rest of the paper is organized as follows.Section 2 is for the development of symplectic eigenvalue equations for wrinkling instabilities of a dielectric elastomer layer.We briefly reviewed the extended W-W algorithm for solving symplectic eigenvalue problems in Section 3.In Section 4,we apply the symplectic method to analyze the critical wrinkling voltage of a constrained dielectric elastomers with and without surface tension.Some concluding remarks are drawn in Section 5.

2 Symplectic equations for wrinkling instabilities in a dielectric elastomer layer

We consider one-dimensional (1D) wrinkling instabilities in a two-dimensional (2D) dielectric elastomer layer (Fig.1),where surface wrinkles can be triggered by applying a voltage to the structure.The wrinkling instabilities have been widely studied through experiments,theories,and simulations.Here we derive asymplectic eigenvalue analysis framework for the problem and provide a powerful and accurate numerical method to solve the highly nonlinear transcendent equations associated with the eigenvalue problems.We adopt the same free energy functions for ideal dielectric elastomer in previous studies[29,30]and assume the dielectric elastomer layer under plane strain condition,such that

(1)

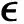
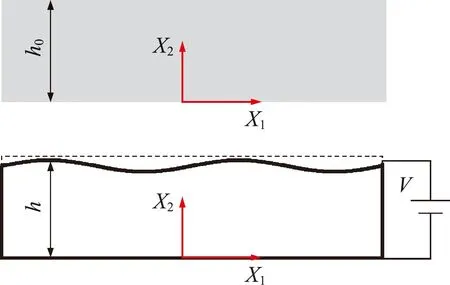
Fig.1 Problem setup of the wrinkles in constrained dielectric elastomer (Top is the reference state of the dielectric elastomer layer and bottom is the schematic of the wrinkled dielectric elastomer layer at the critical voltage)

An augmented free energy function can be derived from Eq.(1) by employing the electric displacement,D=∂W/∂Eas an independent variable through the Legendre-type transform[31]

(2)

whereC=FTFis the right Cauchy-Green tensor.

In this work,we will develop thesymplectic analysis based on free energy function in Eq.(2).It has been shown by Zhang et al.[18]that the positive definite nature of the free energy function is critical for the eigenvalue solver used here.It should be noticed that symplectic eigenvalue problems can still be formed using Eq.(1).

The first Piola-Kirchhoff stress and electric filed vector can be expressed as

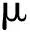
(3)

(4)

whereD⊗Drepresents the tensor product of vectorDandD·(CD) denotes dot product of the vectorDandCD.

The governing equations of the system are,

DivP=0, DivD=0, CurlE=0

(5)

To analyze the wrinkling solution,we decouple the deformation mapping and electric potential into a uniform solution and a perturbed solution[29],suchthat

xi=δijXj+(λ2-1)δi2X2+αui(X1,X2)

(6)

(7)

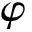
Since electric displacement is the independent variables,we further decouple it into a summation of a uniform and perturbed solution,

(8)

We compute the Taylor series of the electric field vector and the first Piola-Kirchhoff stress in terms ofαand keep the 0thand 1storder,which are given by

E=E0+αE1,P=P0+αP1

(9,10)

whereE0,E1,P0,P1are given in Appendix A.

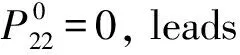
(11)

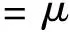
(12)

(13)

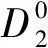
We next analyze the equilibrium equations of the 1storder ofα.Since we focus on the 2D wrinkles,CurlE=0only has one non-zero component,leading to the following equations

L111u1,11+L122u1,22+L212u2,12+

(14)

L222u2,22+L211u2,11+L112u1,12=0

(15)

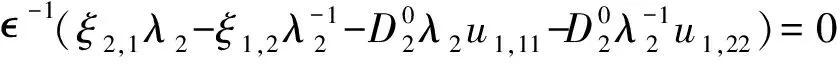
(16)

∂ξ1/∂X1+∂ξ2/∂X2=0

(17)

Eqs.(14,15) are the stress equilibrium equation and Eqs.(16,17) are the Maxwell’s equations,corresponding to CurlE=0and DivD=0,respectively.The boundary conditions are given by

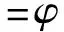
(18)

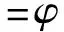
P22(X2,h0)=γu1,22

(19)

To search for the wrinkling solution,we express the variables in Fourier space,such that

u1=exp(ikX1)U1(X2),u2=exp(ikX1)U2(X2)

ξ1=exp(ikX1)Ξ1(X2),ξ2=exp(ikX1)Ξ2(X2)

wherekis the wavenumber.It should be noted that the Fourier modes only apply to the onset instability of the surface.It can be seen from Eq.(19) thatΞ1is not an independent variable and can be expressed as

(20)

In Fourier space,Ψ(X2) can be solved from Eq.(9) as

(21)

We further multiply (ik-1) to Eq.(16) and rearrange equilibrium equations in Eqs.(14～16) in the Fourier space as

K22q″+(K21-K12)q′-K11q=0

(22)

We next introduce the dual variable ofq

p=-(K22q′+K21q)

(23)

The physical meanings of the dual variables are given as follows

(24)

(25)

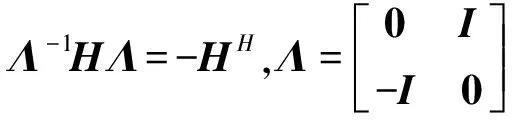
withIas the identity matrix.

The boundary conditions in the Fourier space can be described as

U1(0)=0,U2(0)=0,p3(0)=0

(26)

(27)

3 Extended Wittrick-Williams (W-W) algorithm for symplectic eigenvalue analysis

The symplectic eigenvalue problems defined in Eqs.(25～27) can be effectively and accurately solved by integrating the precise integration method (PIM) and the extended Wittrick-Williams(W-W)algorithm[34].The algorithm has been successfully applied to various engineering applications,such as waves propagation in multilayered structures[12-15],surface wrinkles in neo-Hookean bilayer structures[16,17],and guided waves in magneto-electro-elastic laminated structures[18].Here,we will briefly review the PIM method and W-W algorithm and refer readers to literatures[15,18]for more detailed analysis.

W-W algorithm is based on the eigenvalue count,which represents the number of eigenvaluesin the system under given boundary conditions.The algorithm first rewrites Eq.(25) in the mixed energy format.For a layer within the interval [tI,tII],if state variablesqI,pIIare given,the rest state variablesqII,pIcan be expressed as

(28)

whereFI,GIandQIare complex matrices and can be computed from the following differential equations

(29a)

(29b)

(29c)

For two consecutive intervals[tI,tII] and [tII,tIII] with givenJI,FI,GIandQIfor layer I as well asJII,FII,GIandQIIfor layer II,the relation forqI,pIIIandqIII,pIcan be described as[12,13,15,18]

FIII=FII(I+GIQII)-1FII

(30a)

(30b)

(30c)

and the eigenvalue count

(31)

wheres{#} denotes the number of negative eigenvalues in matrix #.

After applying the PIM method,we can obtain the relationships of the state variable of the dielectric elastomer layer between the top and bottom surfaces as

(32a)

qh=F0,hq0+G0,hph

(32b)

We first compute the eigenvalue count due to the boundary condition atX2=h,which can be written in the matrix form as

(33)

From Eq.(37b),we can further obtain by noticingq0=0

(34)

The total stiffness matrix at the top surface can be expressed as

(35)

Therefore,the eigenvaluecount by incorporating the top surface boundary condition is

(36)

We next consider the boundary condition atX2=0 and solve stiffness matrix from Eqs.(32a,32b,33) as

p0=-R0q0

(37)

AtX2=0,the new boundary condition isp3=0,leading the final eigenvalue count as

J2=J1+sign((R0)33)

(38)

4 Wrinkling analysis in the constrained dielectric elastomer layer

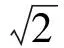
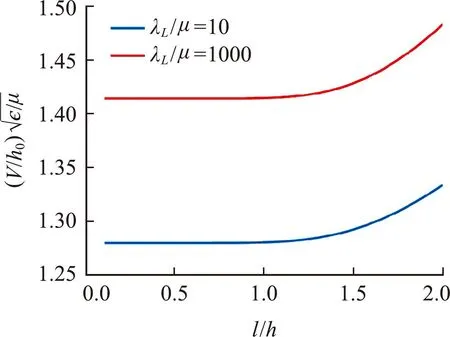
Fig.2 Bifurcation eigenvalue spectrum for the two neo-Hookean layer problems with different Lame constants

Fig.3 Critical voltage VW for the onset of wrinkling(orange dashed line is the analytic solution by Huang[27])

Lastly,we examine the effect of surface energy on the critical voltage for surface wrinkling.Our method is very easy and natural to incorporate the surface energy term,which is given by theγk2term inRSin Eq.(38).A few representative cases are shown in Fig.4.For a finite surface energy,the critical voltage first decreases as the decreases with the wavelength and then increases.This is due to the small wavelength tends to increase the surface area and thus the system energy.Therefore,a minimum voltage will exist.Our results are also in great agreement with the previous analysis[26].

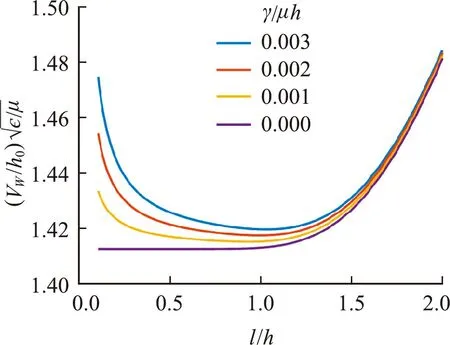
Fig.4 Effect of surface energy on the onset wrinkling bifurcation

5 Concluding remarks

We have successfully demonstrated the applicability of thesymplectic analysis framework in investigating surface wrinkles in constrained dielectric elastomers,where the mechanical deformation is tightly coupled with the electric field.The unique symplectic structure makes it possible to solve the nontrivial boundary value problem efficiently and accurately in the eigenvalue analysis of wrinkles through the extended W-W algorithm and the precise integration method.We validate that the symplectic analysis can obtain the exact wrinkle voltage and wavenumber compared with benchmark results of wrinkles with and without surface energy.The single layer analysis in the current work can be easily extended to multilayer structures with and without periodical boundary condition,which is ready for the analysis of the stability of layered electroactive polymers[35-37]and micro- and macro-instabilities in composite laminated structure instabilities[38-43].Furthermore,the concise mathematical structure of the symplectic analysis allows it adaptable to various multiphysics coupling problems,such as the exploration of magnetoelastic instabilities[44-46].

Acknowledgments

The author expresses sincere gratitude to Prof.Wanxie Zhong for invaluable advising and support,which provided the foundation for this research.Additionally,the author acknowledges the guidance and assistance provided by Prof.Qiang Gao.

Appendix ATaylor series of the electric field vector and the firstPiola-Kirchhoff stress

(A1)

(A2)

(A3a)

(A3b)

(A3c)

(A4a)

(A4b)

(A4c)

(A4d)

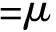
Appendix BThe stiffness matrices in Fourier space

(B1)

(B2)

(B3)

Appendix CThe precise integration method for the eigenvalue count

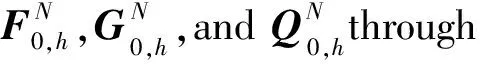
(C1)

(C2)

(C3)

(C4)

where

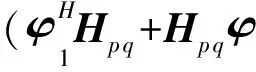
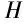
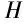
(C5)

(C6)

(C7)

and

(C8)

wherel=N-1,…,1,0.