市政道路开挖对埋地管道力学行为变化影响

黄小苑

(广东省源天工程有限公司,广东 梅州 514000)

埋地管道是水、石油和天然气的主要运输工具。由于埋地管道与路面地层直接接触,地层对管道的影响非常明显,尤其是对于地质环境较为复杂的长距离管道。因此,埋地管道容易受到各种地质灾害的威胁,可能导致管道大变形、管道断裂,甚至导致油气泄漏。一旦发生这种情况,将导致环境污染,并使油气资源停止运输[1]。此外,市政道路开挖引起的地层沉降是威胁和破坏埋地管道的主要地质灾害之一。因此,市政道路开挖引起的地层沉降下埋地管道的力学行为,对埋地管道的安全运行具有重要意义。

目前,已有众多学者研究埋地管道破坏与地层之间的研究,夏润禾[2]通过有限元法研究埋地钢管在地震下的力学行为,充分考虑了管道与土壤的非线性接触行为,重点研究土壤和管道参数对管道局部屈曲的影响。在此基础上,苏义宝等[3]建立简单有效的理论模型来解释埋地管道的局部屈曲行为。黄虎等[4]采用应变分析方法研究了地质灾害区埋地管道的力学行为。周晨等[5]基于非线性数值模拟方法,考虑大应变下管道与土壤的非线性接触行为,研究了沉陷区埋地管道的变形机理。

尽管对埋地管道力学行为的研究很多,但基于市政道路开挖引起的地层沉降对埋地管道等效应力、应变和位移的系统研究仍然缺乏。因此,对地层沉降条件下埋地管道力学行为进行定量分析的研究十分必要。基于此,本文建立了地层沉降下埋地管道的有限元模型,研究了埋地管道的力学行为。基于管土相互作用,讨论管道参数、土层厚度对埋地管线力学行为的影响。

1 数值模拟模型

1.1 模型分析

市政道路开挖后,路面地层扰动导致埋地管道不均匀沉降是管道变形的主要原因。假定管道为弹性地基梁模型来计算管道的竖向位移[6]。目前,广泛采用 Winkler模型作为线性弹性地基模型,其挠度微分方程见式(1):

(1)

其中,设定q(x)=0,对应的齐次微分方程见式(2):

(2)

其中,E为管道的弹性模量,MPa;I为管段的惯性矩,m4。引入积分常数计算式(2)齐次方程的一般解见式(3)[7]:

y=eβx(A1cosβx+A2sinβx)+e-ax(A3cosβx+A4sinβx)

(3)

其中,β为特征系数;eβx和e-βx用双曲函数表示,见式(4):

eβx=chβx+shβx,e-βx=chβx-shβx

(4)

由Peck土体沉陷方程推导出了由开挖工程所造成的地表沉陷方程,并用高斯正态分布方程表示了开挖工程中的地表沉陷。但是,该方法的计算十分麻烦,所得的结论也较为复杂,并不适用于市政道路开挖工程实践。为此,为降低计算工作量并精确地解决管线变形问题,本文利用二次函数替代高斯正态分布法,对管线变形问题进行了专门的解法[8],并将埋地管道变形问题表达为式(5):

y(x)=ax2+bx+c

(5)

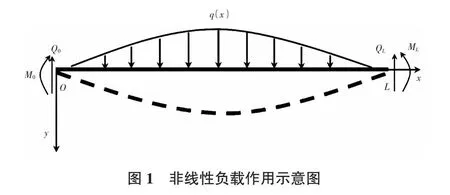
当土壤位移近似为二次函数时,埋地管道的荷载如图1所示。式(5)中的a,b和c(参数)可根据图1中的边界条件求得。

1.2 数值模拟模型

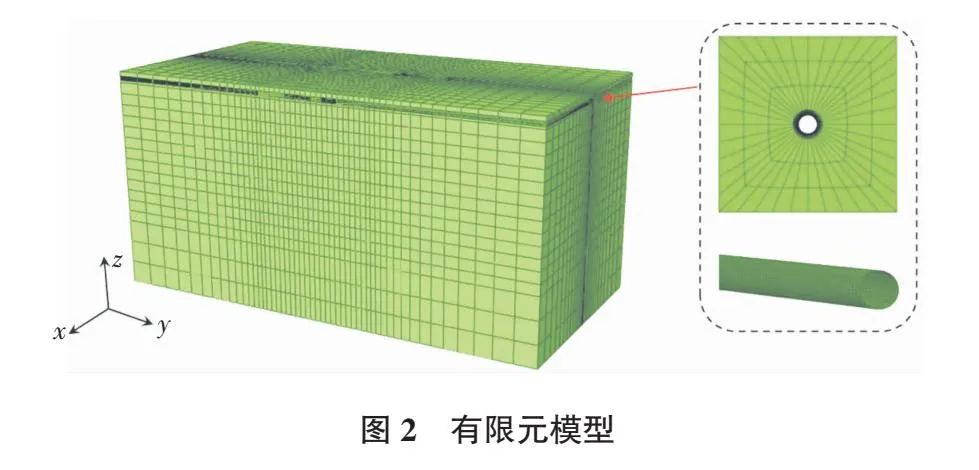
整个计算模型由土壤和埋地管道组成。为了节省计算成本,提高计算效率,对整个模型进行一定程度的简化。假设市政道路开挖为明挖。整个模型的尺寸为400 m×200 m×200 m。矿区面积为200 m×100 m×20 m(w=100 m,v=20 m),路基埋深为1.2 m(H=1.2 m)。市政道路开挖沿轴线进行纵向明挖。开挖过程分为10步,每步开挖长度为0.5 m。将开挖长度定义为“EL”。埋地管道直径660 mm(D=660 mm),壁厚8 mm(t=8 mm),埋深6 m(h=6 m)。图2为有限单元模型。在计算过程中,埋地管道的计算使用四结点S4R (Simpless Node Response Architecture,S4R),并在管道的纵向上布置了5个积分点。利用八结点的简化积分器(C3D8R)处理土壤。将地下管线附近的土体单元划分得更细,以增加其模拟的准确性。对模型进行分析时,首先要对整个模型施加初始地应力场。其次,如果存在内压,则需要首先对模型施加内压。最后,对市政道路进行挖掘,直至结束[9]。除顶部外,对整个模型施加法向约束,对管道施加轴向约束。定义管道的x轴为水平方向,z轴为垂直方向。

本文以X65无缝钢管为研究对象。其密度为7 800 kg/m3,杨氏弹性模量为210 GPa,屈服强度为448.5 MPa,泊松比为0.3。管道的应变速率和应变硬化对变形过程有显著影响,在分析过程中应加以考虑。埋地管道铺设在淤泥质黏土上,市政道路路基层为页岩[10]。假设各土层分布各向同性,无淤泥和岩石,各层界面水平。采用摩尔-库仑构成模型来描述土的力学行为。各土层的参数见表1。

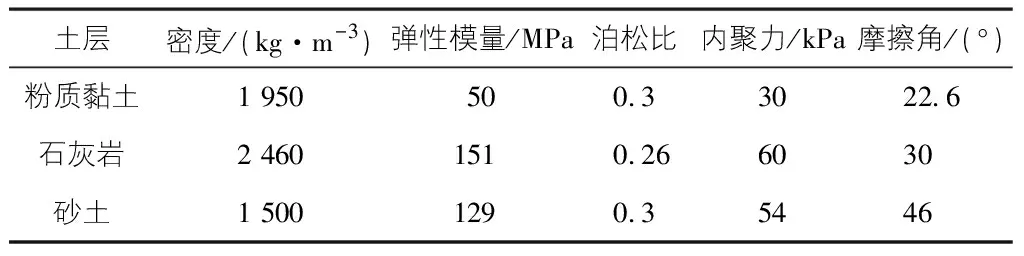
表1 土壤材料参数

在管土相互作用中,埋地管道与周围土壤直接接触。在沉降过程中,应考虑管道的力学参数、土壤构成模型和管土变形特征对管土接触单元的影响。因此,基于接触理论,管道与土壤之间的接触算法由接触惩罚函数定义。管道与土壤界面的摩擦系数设定为 0.3。

2 结果分析与讨论

2.1 地层位移和管道位移变化

图3为不同开挖长度下的路面地层位移和管道位移。从图3(a)中可以看出,在开挖长度为20 m(EL=20 m)的市政道路开挖工程中,开挖工程对地面及管线的作用不大。在挖掘长度的增大过程中,道路路面表层产生了位移,与此同时,路面地层位移范围沿挖掘方向变大。最大地层位移出现在路面上表面,最大地层位移随着开挖长度的增加而增加。市政道路上表面的位移表现为地层沉降,而道路下表面则表现为隆起。从图3(b)中可以看出,埋设管线在EL=20 m时,首先发生了水平移动,但移动量很小,其最大移动只有0.002 m。由于开挖区最初并没有直接位于管线下面,并且在x轴上与管线中心有一定的偏离。这样,当地应力解除时,管线就会朝路基一侧倾斜。当EL>100 m 时,开挖区从管道的一侧转向另一侧。从图3(c)可以看出,管道的垂直位移随着挖掘长度的增加而增大。当EL=20 m 时,最大垂直位移0.003 m,当EL=200 m 时,最大垂直位移为0.094 m,增加约31倍。当EL=100 m 时,最大垂直位移0.034 m,仅增加10倍,但此时水平位移已达到最大值。但在整个开挖过程中,垂直位移远大于水平位移,说明市政道路开挖区在垂直方向上对管道的影响更大。在整个挖掘过程中,管道的水平位移和垂直位移使得管道的三维变形相对复杂。

2.2 土层厚度

土层与埋地管道直接接触。而管道周围的土壤变形是由市政道路开挖引起的,使埋地管道变形。周围土层的特性直接影响埋地管道的应力。因此,对路面土层厚度(L)进行了研究,L分别设定为10 m,15 m,20 m,25 m和30 m。

当管道埋深为6 m时,不同路面土层厚度下埋地管道的Von Mises 应力和圆周应变变化如图4所示。从图4(a)中可以看出,埋地管道的最大应力随路面土层厚度的增加而近似线性增加,变化非常明显。同时,管道中部的高应力区向轴向扩展。当厚度为10 m(L=10 m)时,最大应力为116.3 MPa。当L=30 m 时,最大应力为172.1 MPa,增加48%。管道中部(y=200 m)的圆周应变如图4(b)所示。管道上表面的应变略大于下表面的应变,最大应变位于管道上表面(90°)。随着路面土壤厚度的增加,管道的圆周应变也随之增加,但变化率逐渐减小。

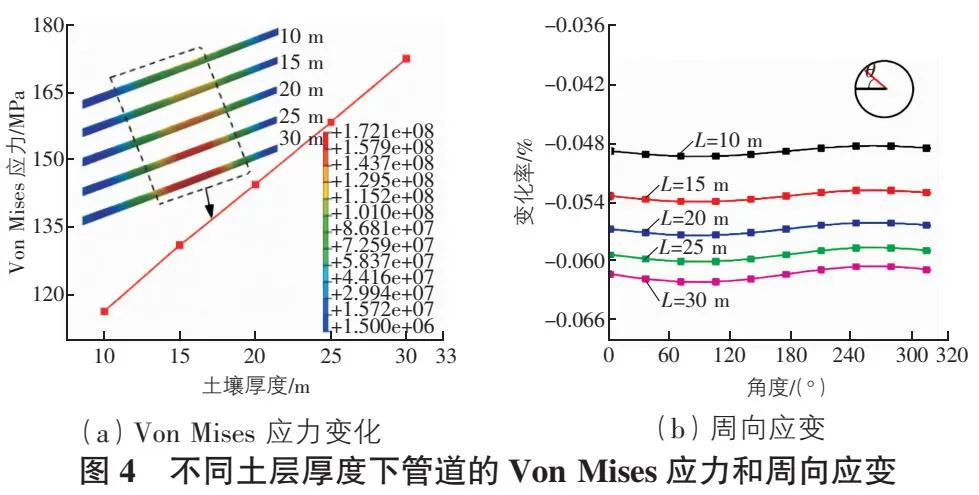
图5为不同路基土层厚度下的地层位移和管道垂直位移。在地层位移方面,随着厚度的增加,道路开挖区上表面的沉降量增大,而下表面的沉降量影响不大。如果市政道路开挖区上表面的沉降量过大,开挖区周围的土体就会失稳并遭到破坏,从而可能导致开挖区上表面塌陷。因此,管道将进一步变形。对于管道的位移,不同周围土层厚度下管道的位移曲线在采空区外开始分离。在远离采空区的边界(y=0 m和y=400 m),位移曲线近似重合,这说明它不受周围土层厚度的影响。管道的最大位移和变化率随周围土层厚度的增加而增大。当L=10 m时,管道的最大位移为0.095 m;当L=30 m时,最大位移为0.12 m,增加25%。结果表明,在铺设管道时,不仅要考虑开挖区对管道的影响,还要考虑管道周围土壤地质的影响。为了减小管线的弯曲变形,必须选择合适的土层厚度,以延长管线的使用寿命。

2.3 管道埋深

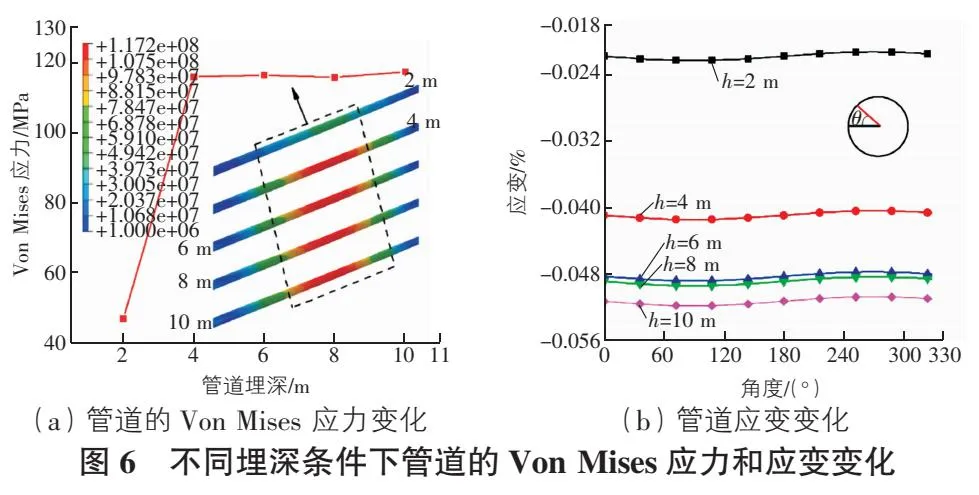
管道的埋深决定了管道覆土压力的大小。管道埋深越深,管道的覆土压力越大。当管道直径为660 mm、壁厚为 8 mm时,不同埋深下管道的Von Mises应力和应变变化如图6所示。从图6(a)中可以看出,当埋深为2 m(h=2 m)时,管道的最大应力仅为 46.7 MPa,且高应力区域较小。随着埋深的增加,最大应力也随之增加。当h=10 m时,最大应力为117.2 MPa,增加了151%。但当h>4 m时,最大等效应力的变化很小,小于2 MPa。管道中部(y=200 m)的应变如图6(b)所示。管道上表面的应变略大于下表面的应变,最大应变位于管道上表面(90°)。随着埋深的增加,管道的应变增大,变化率先减小后增大。

3 结论

1)在开采过程中,管道的最大Von Mises 应力和最大垂直位移位于管道中部。管道中存在应力集中现象,但未出现屈服变形。随着开挖长度的增加,Von Mises 应力、应变和垂直位移均增加,但水平位移先增加后减小,直至为零。管道的垂直位移大于水平位移。此外,最大地层位移出现在开挖区的上表面,存在一定的地层沉降。

2)随着管道直径、厚度比和埋深的增加,管道的最大Von Mises 应力、圆应变呈非线性增加。随着周围土层厚度的增加,Von Mises 应力呈线性增加,应变和位移呈非线性增加。此外,管道的最大Von Mises 应力、应变和最大位移随开挖区宽度和高度的增加而增大,随采空区埋深的增加而减小。