基于小波降噪的深基坑地表沉降预测研究★
2024-02-27田海川董玉雄马林杰
于 磊,田海川,张 博,张 纯,董玉雄,马林杰
(北京市政路桥股份有限公司,北京 100000)
0 引言
近年来,随着社会经济的不断发展,城市的建设逐渐转入地下发展。随着深基坑的开挖深度不断加大,势必增加了施工风险。对基坑开挖过程中收集到的监测数据进行有效的分析和预测,能够帮助及时的调整支护方案,合理安排施工进度,从而有效保证施工安全[1-6]。因此,对深基坑开挖过程中的沉降变形进行控制和预测是当前的主要任务。
目前,已有大量学者针对基坑监测数据的分析与预测进行了研究。牛全福等[7]采取一种基于Kalman去噪的ARIMA-NAR神经网络组合模型进行预测分析。付欣等[8]使用改进的BP神经网络对哈尔滨某地铁车站深基坑土体沉降变形进行预测研究。张蓓等[9]利用权值参数以及梯度下降的方法对小波网络模型进行了优化和修正,并且工程实例证明,改进后的模型能使预测值更贴近于实测值。蒙国往等[10]对围护结构自动化监测设备进行实地调研,提出结合BP人工神经网络模型对围护结构水平位移进行多步滚动预测的方法。赵华菁等[11]以苏州某地铁车站深基坑工程证明了LSTM深度网络预测模型比BP神经网络预测模型具有更高的精度,更适用于预测地连墙变形问题。
综上所述,大多数学者通过神经网络研究了深基坑开挖变形规律。但是由于各类误差的存在,对于深基坑开挖周围环境变形的预测有一定局限性。本文在前人研究的基础上,基于保定市汽车科技产业园深基坑工程大量监测数据,采用Mallat算法,将监测数据进行特征提取,并通过低通滤波,达到去噪的目的。最后通过径向基神经网络(Radial Basis Function Neural Network)对降噪后的监测数据进行预测分析。
1 工程概况
1.1 工程背景
本研究依托于位于保定市的长城汽车科技产业园市政道路建设项目永华大街(南二环—太行路)排水工程顶管工作井。基坑开挖深度达到10.38 m,基坑周长约80 m。边坡采用80 厚C20挂网喷射混凝土面层,面层插筋采用16@1 500 mm×1 500 mm,插筋长度1.2 m,如图1所示。
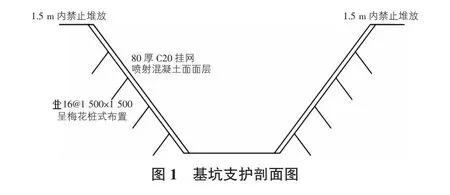
1.2 工程地质条件
根据地勘报告,勘察深度20.00 m内将土层共分为7层,除表层为素填土外,其下均为第四系全新统冲、洪积成因的土层,土体的物理力学参数见表1。
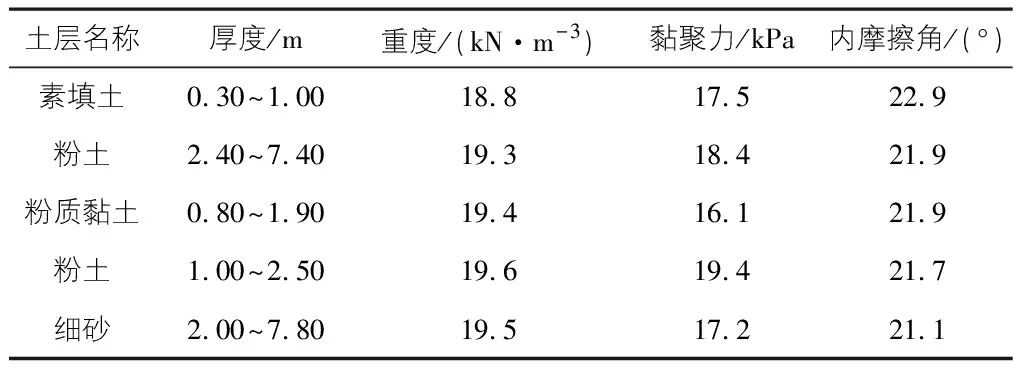
表1 土层物理力学参数
1.3 监测方案设计
按设计要求,沿基坑边布设周边地表沉降断面,每断面上测点距基坑边缘2 m开始向外布设,纵向、横向间距均为10 m,梅花形布置,每断面向基坑外延伸5 m。该基坑工程地表沉降监测点平面布置图和剖面图如图2,图3所示。
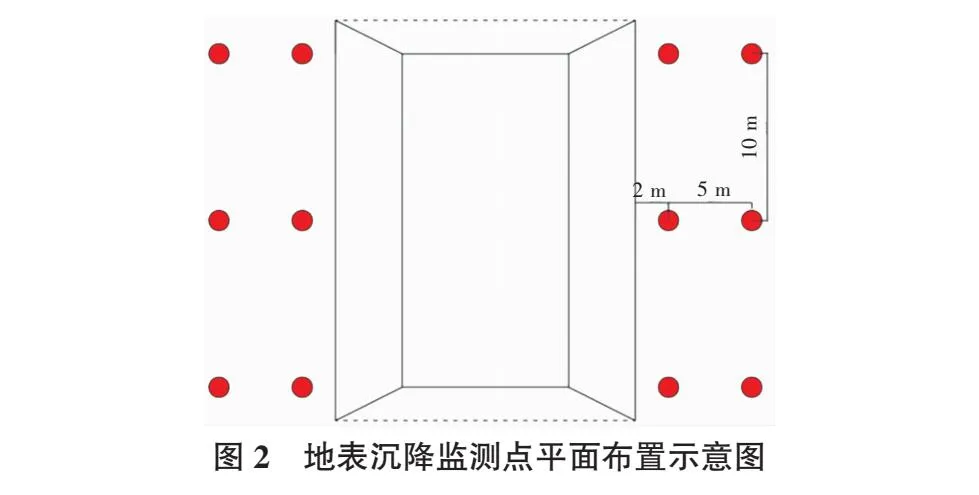
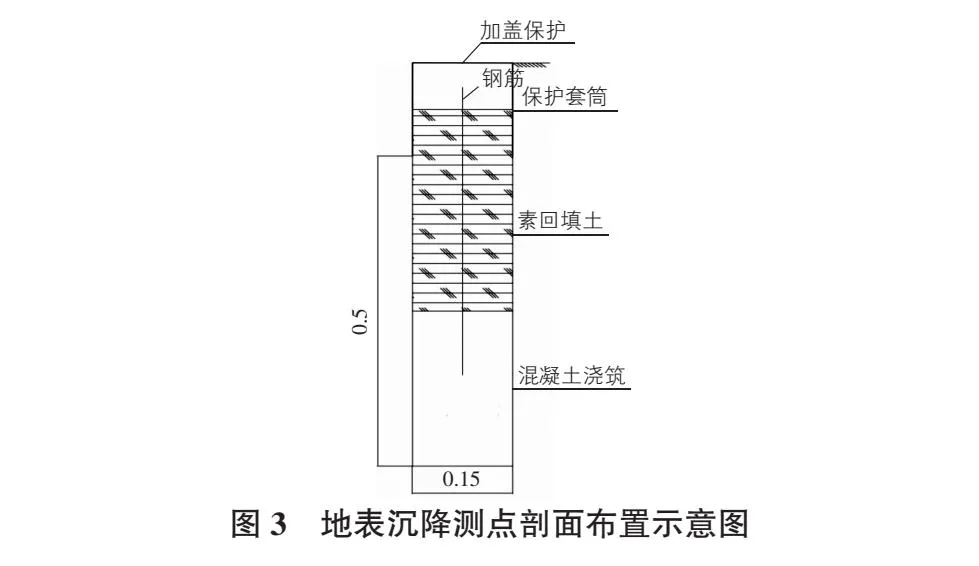
2 小波变换和神经网络
2.1 小波去噪原理
定义小波函数ψ(t)∈L2(R)在时域上是有限的。也就是说,ψ(t)的值在某个范围内,其他的方为零。小波的特性是零均值和归一化。从数学上讲,它们表现为:
(1)
(2)
根据母小波的扩张和平移性质,小波可以形成一个基集,表示为:
(3)
其中,u为平移参数,表示信号中的真实信号;s为大于零的缩放参数,因为负缩放未定义。多分辨率性质确保所获得的集合{ψu,s(t)}是正交的。从理论上讲,小波变换是ψu,s(t)的系数,表示为:
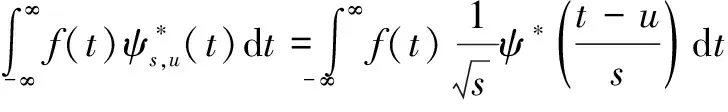
(4)
通过该变换,可以将一维信号f(t)映射到二维系数Wf(s,u)。这两个变量可以执行时频分析。由此可以知道在某个时刻(参数u)定位特定频率(参数s)。
如果f(t)是L2(R)的一个函数。逆小波变换是:
(5)
其中,Cψ定义为:
(6)
其中,Ψ(ω)为小波ψ(t)的傅立叶变换。这个方程也称为容许条件。
在利用小波变换进行信号去噪时,目前使用较多的小波函数有Haar,Biorthogonal和Daubechies。许多学者证明[12-13],Daubechies小波(简称db小波)运算速度快,可以对信号进行局部分析,对信号的变化特征还原较好。因此,本文采用db小波对深基坑监测数据进行降噪处理[14]。
2.2 RBF神经网络
径向基神经网络(Radial Basis Function Neural Net work)起源于为在多维空间中执行一组数据点的精确插值而开发的技术。RBF神经网络是一个具有单个隐藏层的前馈型神经网络[15-17]。
神经网络的结构图如图4所示。
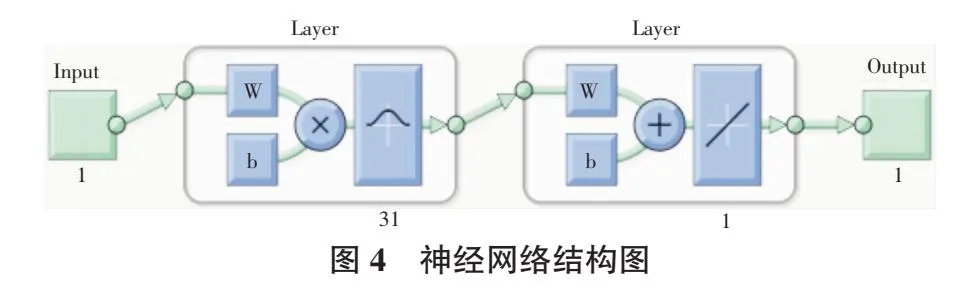
隐藏层的每个节点都有一个基函数,用于与网络输入向量进行比较并产生具有径向对称响应的输出。响应取决于径向函数的类型。然后将隐藏层的响应与输出层的突触权重线性组合。最后,通过激活函数产生网络输出。
上述RBF神经网络中的基本计算包括:
1) 输入层计算。
在隐单元l的输入处,输入向量x根据输入权重wh进行加权:
(7)
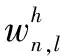
2)隐藏层计算。
隐藏单元l的输出由以下公式计算:
(8)
其中,隐藏单位l的激活函数φl(·)通常选择为高斯函数;cl为隐藏单元l的中心;σl为隐藏单元l的宽度。
3)输出层计算。
网络输出m通过以下公式计算:
(9)

本文采用平均绝对误差MAE、均方根误差RMSE和平均相对误差率ARER三个评价手段对最终的预测结果进行评价分析,即:
(10)
(11)
(12)
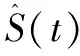
3 工程应用
3.1 三维有限元模拟
为更好地验证基于小波降噪的RBF神经网络对地表沉降的预测值,采用MIDAS GTS NX软件对深基坑开挖过程进行模拟,对比模拟数据与监测数据,并以此作为之后RBF神经网络预测的基础。
3.1.1 模型边界条件确定
模型与实际工程等比例建立,基坑边长约为18.5 m。基坑外模型边长按照经验应取实际基坑边长的4倍~6倍,模型深度为实际深度的3倍~5倍,所以基坑外模型边长取60 m,深度取40 m。基坑支护采取喷锚支护的方式。对于模型的约束条件上,模型四周面约束其法向的位移,底部约束其三个方向的位移。
3.1.2 土体本构模型及网格的划分
在建立有限元模型之前,需要选择土体本构模型。本模型选择的是修正摩尔-库仑模型作为土体本构模型[18]。对比于普通的摩尔-库仑模型,修正摩尔-库仑模型模拟出的结果更贴切于深基坑开挖土体卸荷的过程。网格的大小直接影响到计算的精度,模型提取的结果主要集中在基坑模型附近,因此对这一部分的网格划分较细,本计算模型单元数12 460,节点数10 718。模型如图5所示。
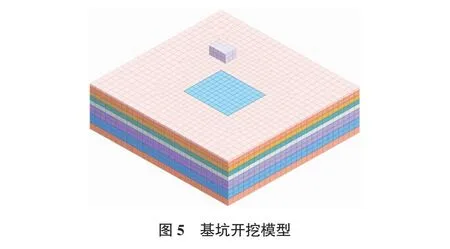
3.1.3 施工工况
开挖分为10步进行,见表2。开挖前,进行初始地应力的平衡,将Z方向的位移清零。

表2 施工工况
3.2 模拟结果与监测结果分析
选取基坑北面地表沉降监测点DB-4实测值与数值模拟结果进行对比,如图6所示。

由图6可以看出,实际监测值与有限元模拟值的变化趋势大致相同,说明有限元软件对于基坑开挖地表沉降预测有一定的可靠性。监测点DB-4实测值最大沉降为8.12 mm,模拟值最大沉降为7.11 mm。这是因为在实际的施工过程中,地表受到附近施工的影响,使得实际值偏大。基坑开挖过程地表沉降竖向位移云图如图7所示。

3.3 小波参数选取
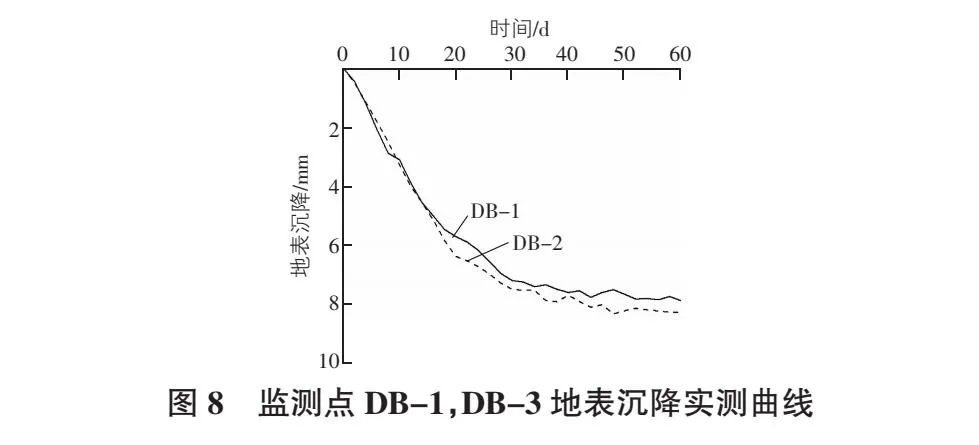
监测点DB-1,DB-3地表沉降实测曲线如图8所示。
在对监测点DB-1,DB-3沉降数据进行多次降噪验算后,选取降噪效果较好的db10小波函数进行降噪,降噪次数选择1,2,3,不同降噪次数后的地表沉降变化如图9所示,不同降噪次数的误差曲线如图10所示。
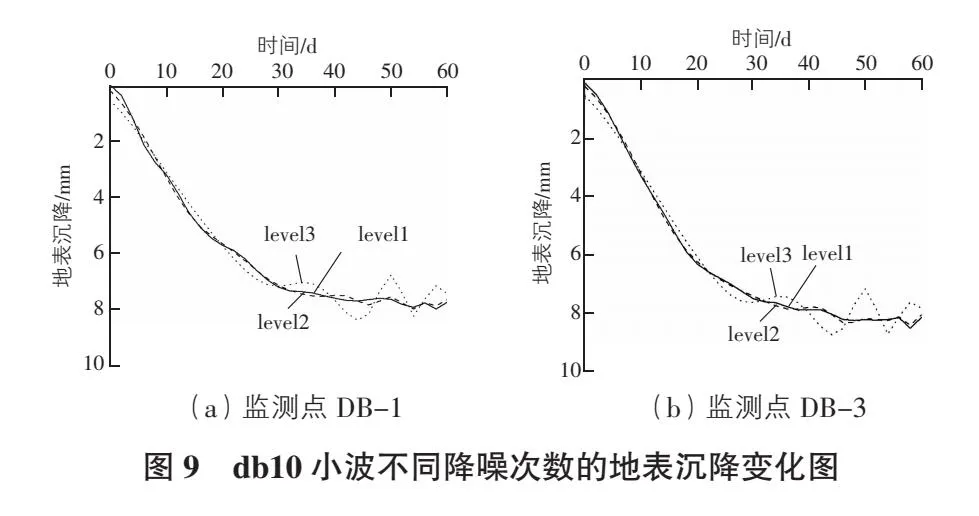
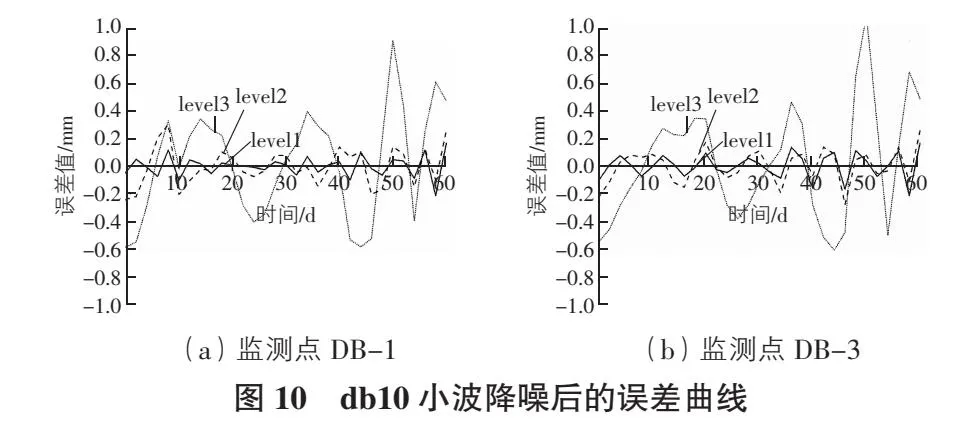
由图9可以看出,不同的降噪次数的地表沉降变化曲线均与实测曲线变化趋势保持一致。但由图10可知,降噪次数为3(level=3)的误差最大,降噪次数为1(level=1)误差最小,小波去噪效果最好,并且误差范围小于±0.2 mm,因此,本文选取db10、尺度1的小波进行去噪处理。
由以上分析可知,经过db10尺度为1的小波降噪后,可以最大程度的保留数据的细节特征并且去掉其高频信号,使得监测点DB-1,DB-3的地表沉降变化特征更加明显。
3.4 地表沉降预测与分析
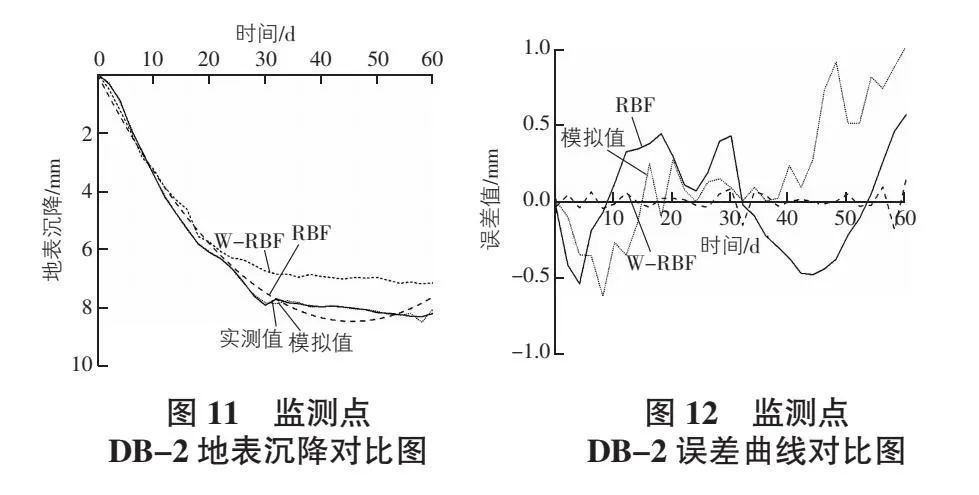
为了探究小波变换对地表沉降预测的影响,本文采用RBF神经网络对监测点DB-2的地表沉降监测数据进行预测。图11给出了实测值、RBF神经网络预测值、经过降噪后的RBF神经网络预测值以及有限元模拟值的对比曲线,图12为三种方法的误差值对比曲线,表3为最终误差结果。
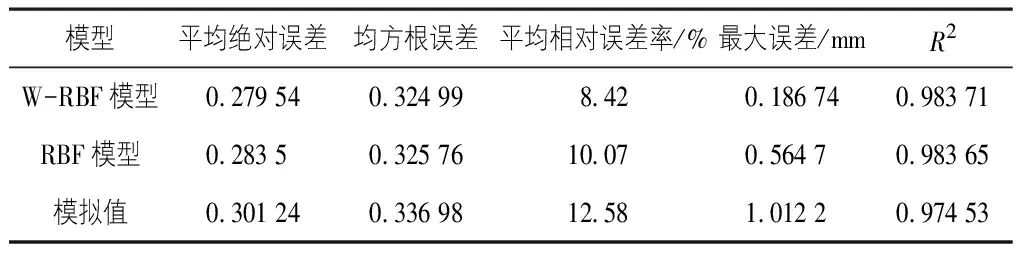
表3 降噪与未降噪预测值对比分析
从图11,图12,表3可以看出,在同样条件下,经过小波降噪的监测数据平均绝对误差为0.279 54、均方根误差为0.324 99、平均相对误差率为8.42%、最大误差为0.186 74 mm,R2为0.983 71,均优于未降噪的预测值和有限元软件的模拟值。经过实际工程证明,经过小波降噪的RBF神经网络预测值与实际值吻合较好,误差较小,可以满足实际工程的需要。
4 结论
本研究基于保定市汽车科技产业园深基坑工程,对地表沉降监测值进行小波降噪并使用RBF神经网络对降噪后的监测数据进行预测分析,得出了以下结论:
1)通过对监测数据多尺度分解,分离出监测数据中的真实信号与噪声信号,并对这些高频的噪声信号进行过滤,可以有效地达到降噪的目的。
2)本文提出基于小波降噪的径向神经网络预测思路,并且测得W-RBF模型的平均绝对误差为0.279 54、均方根误差为0.324 99、平均相对误差率为8.42%、最大误差为0.186 74 mm,R2为0.983 71,通过对比,均优于RBF模型。
3)经过实际工程验证,小波降噪的RBF神经网络模型具有较高的精度,预测值与实际值误差小,能够满足实际工程的需要。深基坑开挖对周围地表沉降的影响是一个很复杂的问题,在建立有限元模型以及RBF神经网络模型的时候并未考虑到基坑附近施工的影响以及临时荷载的影响,所以对基坑周边地表沉降的预测仍存在一定误差。因而在之后的研究中应该充分考虑各种施工因素,提高预测的准确度,为实际工程提供参考。
