直线共轭内啮合齿轮传动的齿形参数研究

杨晓东，崔建昆

（成都飞亚航空设备应用研究所有限公司，成都 611130）

0 引言

直线共轭内啮合齿轮传动，也称为直齿共轭内啮合齿轮传动，最早由瑞士人Paul Truninger提出，用于内啮合齿轮泵[1]。在直线共轭内啮合齿轮传动中，外齿轮的齿廓是直线，内齿轮的齿廓是与之共轭的曲线，由于其齿廓曲率小，接触强度高，具有一些特殊的啮合特性，作为内啮合齿轮泵中的齿轮副使用时，可以得到困油容积小、流量脉动和噪声小的效果[2-3]。

目前国内外对直线共轭内啮合的研究都集中在其齿轮泵的应用方面，作为一种齿轮传动形式，其啮合原理和传动性能的研究非常不充分，至今还没有完整的齿形参数计算标准[4]。因此其应用范围狭小，相关啮合理论的研究也非常少见[5-6]。

近年来，由于直线共轭内啮合齿轮泵的优良性能逐渐被工业界认可，并在伺服液压系统等新兴技术领域得到推广运用，其产品研发和性能改进也受到企业的重视[7]，从而带动对这种特殊齿轮传动的深入研究，不少学者也开始探讨直线共轭内啮合齿轮副在机械动力传动领域的应用价值[8]。本文通过对直线共轭内啮合齿轮副的啮合过程分析和齿形参数研究，定义了外齿轮直线齿廓的基本参数，建立了齿廓坐标方程，在此基础上对齿廓上啮合极限点、压力角、啮合线、直线共轭内啮合齿轮传动及其重合度等进行了系统分析，研究了齿廓线段与对应啮合转角之间的关系，提出了保证连续传动条件下齿形参数设计方法，并通过工程实例验证了齿形参数设计方法和直线共轭内啮合齿轮副的啮合性能，对拓宽其应用领域具有一定的意义。

1 外齿轮参数和齿廓方程

直线共轭内啮合齿轮副中，外齿轮的齿廓是左右对称的直线，其齿顶和齿根分别是一段圆弧，如图1所示。

图1 外齿轮直线齿廓

以外齿轮中心O1为原点建立坐标系O1X1Y1，外齿轮的齿廓方程可以通过多个几何参数来建立，如齿轮的齿形角、分度圆弧齿厚、齿廓与齿轮中心的距离等。但是，从工程实用的角度，对于直线共轭内啮合齿轮副，使用一个类似于渐开线齿轮模数的参数用于齿轮的几何计算，更容易进行后续的分析研究，以及与渐开线齿轮进行性能比较。

在渐开线齿轮中，模数与分度圆有关，规定齿廓曲线在分度圆上的压力角为标准值，是渐开线齿轮分度圆的一个重要特征[9-10]。对于标准渐开线齿轮，分度圆位于齿廓啮合区的中间位置，可以有效地控制啮合过程中压力角变化范围，保证齿轮的传动效率。同样，直线齿廓外齿轮上的压力角在齿廓各点也不一样，压力角对传动性能同样会产生影响，仿照渐开线齿轮的参数设置，定义外齿轮分度圆上的压力角为标准压力角α，则齿顶半角公式为

式中，θ为外齿轮分度圆弧齿厚s所对应的圆心角，不考虑啮合间隙的情况下，规定外齿轮分度圆上齿厚s等于齿间距e，因此

式中，z1为外齿轮齿数，则有

可见齿顶半角与齿数有关，压力角一定时，齿数越小齿顶半角越小，两者的关系如图2所示。

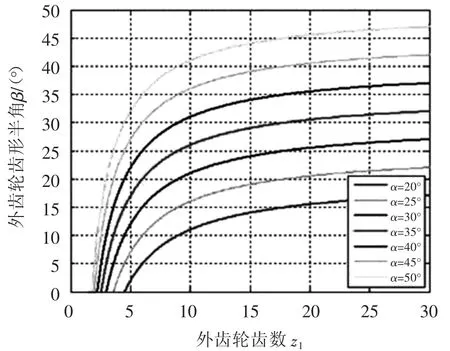
图2 齿形半角与齿数的关系

由于β不能为负值，因此对于给定的压力角，齿轮会有一个最小的齿数，如当分度圆压力角α为20°时，外齿轮的最小齿数为5，对应的齿顶半角β为2°，齿轮的形状如图3所示。

图3 α=20°，z1=5的直线齿廓外齿轮

仿照渐开线齿轮来定义模数，作为直线齿廓外齿轮的基本参数。

式中，p为外齿轮分度圆齿距。

齿轮的左侧齿廓直线方程为

式中，r1为外齿轮的分度圆半径。

从式（1）可以推导出直线齿廓外齿轮齿廓上k点的压力角为

式中，θk为轮齿上过k点的弧齿厚所对应的圆心角。

可见齿廓压力角随着半径的增加而减小，理论上当齿顶宽度为零时，最小压力角等于齿顶半角β；而最大的压力角出现在外齿轮齿根啮合的位置, 与渐开线齿轮相比较，其压力角沿齿高方向变化的趋势相反，同时变化的幅度也小得多。因此可以预见，两种齿轮的传动特性也会有较大的区别。

2 直线共轭内啮合传动

直线齿廓外齿轮按照平面啮合原理，可以和一个共轭的内齿轮组成内啮合齿轮副,当满足定传动比条件时，两个齿轮的运动相当于一对节圆的纯滚动，节点P为两个节圆的内公切点，位于内外齿轮中心O1、O2的连线上，如图4所示。

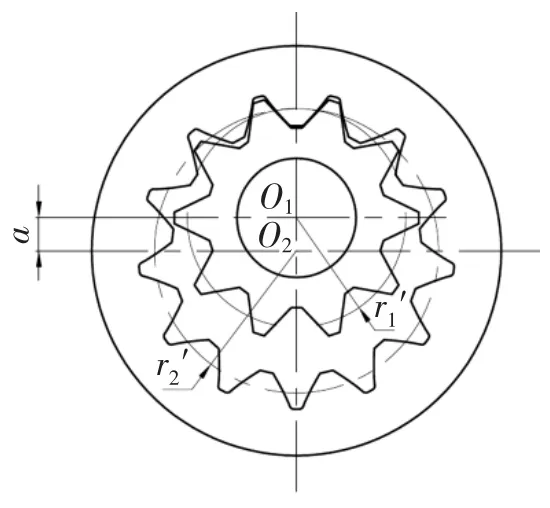
图4 直线共轭内啮合齿轮副

齿轮的节圆半径r1′、r2′可以根据传动比i及实际啮合中心距a′计算：

式中，z2为内齿轮齿数。

对于同样一个直线齿廓外齿轮，可以在不同的中心距下与齿数为z2的内齿轮共轭，实现同样传动比的传动，对应内齿轮齿廓可以通过共轭原理进行计算，不过在不同的中心距下得到的内齿轮共轭齿形是不一样的，这一点与渐开线齿轮副有区别。

把内齿轮齿廓上压力角为标准值的点也定义为其分度圆位置，如果啮合时，直线齿廓外齿轮的节圆与其分度圆重合，由于啮合的一对齿轮节圆压力角相同，因此共轭内齿轮的节圆也与其分度圆重合，这种啮合状态定义为直线共轭标准内啮合，两个齿轮必须具有相同的模数，啮合中心距为

由式（10）定义的中心距a称为标准中心距。如果中心距大于或小于标准中心距，内外齿轮也可以啮合，构成变位的直线共轭内啮合。需要再次指出的是，由于不具备渐开线齿轮的可分性，不同中心距下啮合的直线共轭齿轮副，内齿轮齿廓共轭曲线是不同的，因此直线共轭内啮合齿轮传动的变位问题的研究要复杂得多。

3 齿廓啮合极限点

式（5）表述的外齿轮齿廓，是一条可以无线延伸的直线，但是实际上轮齿的高度是有限的，设计时需要合理选取该直线的一段作为轮齿齿廓，图5所示的直线外齿轮齿廓，其齿顶最高不超过齿廓与对称轴的交点A，由齿廓方程式（5）、式（6）可得

图5 直线共轭内啮合的齿廓啮合极限点

其实，点A不一定就是内外齿廓啮合时的极限点。经过直线齿廓上的任意一点M（xm，ym）作齿廓的法线，交节圆于P1点；将M点连同其法线沿齿廓向上平移，P1点也在节圆上向右移动，最终到达与节圆的切点Pc，此时齿廓上对应点C（xc，yc）为齿廓啮合极限点，超过啮合极限点的齿廓直线段没有共轭曲线，可能在啮合过程中发生齿廓干涉，因此在齿轮设计时，齿轮的齿顶不能超过C点。

啮合极限点C的坐标可由下式计算：

图4中，N点为直线齿廓上过啮合极限点C的法线与坐标轴Y1的交点，有

将式（11）代入式（14），得

很明显，C点的位置不仅决定于直线齿廓本身的参数，还与与齿轮副的传动比及中心距有关。对于相同模数和齿数的直线齿廓外齿轮，其啮合极限点的位置与齿顶半角β有关，β越大，极限点位置越高，当C点与A点重合时，可得

仿照渐开线齿轮的参数设计方法，直线齿廓外齿轮齿顶圆半径与分度圆半径之差为齿顶高：

由于长度CN的计算比较方便，齿轮参数设计时，可以采用如下限制条件：

图4中，外齿轮齿槽两侧的直线齿廓，在齿根相交于B点。显然齿廓工作时啮合点不能在B点以下，B点为直线齿廓上齿根的极限位置，外齿轮中心到B点的距离为

定义直线齿廓外齿轮分度圆半径与齿根圆半径之差为齿根高：

式中，c*为顶隙系数。

4 啮合线及其特性

根据上一节的分析，直线齿廓外齿轮可以选择齿廓直线上BC点之间任意一段长度作为齿轮的齿面轮廓线，与共轭的内齿轮形成内啮合传动。但是在实际工况条件下还要考虑连续传动要求，重合度应不小于1。较大的重合度可以提高传动的平稳性，提高承载能力，但是在一些特殊的场合，如内啮合齿轮泵中，重合度过大会引起严重的困油。

啮合线是齿轮副啮合过程中，啮合点在固定坐标架中的轨迹，可以通过齿廓法线法来进行求解。啮合线可以表达齿轮副的啮合特征，还可以用于共轭齿廓的计算以及重合度的分析。

齿轮传动的重合度主要与轮齿的高度有关，渐开线齿轮的重合度与齿高的关系近似于正比例关系，因为其啮合线为直线。因此，在齿形设计时，选择不同区段的渐开线作齿廓，齿轮高度基本上没有太大的差别。但是对直线共轭内啮合传动的啮合过程分析发现，其重合度与齿高的关系与渐开线齿轮完全不同。

如图6 所示，过节点P作外齿轮齿廓g1的垂线，垂足为啮合点m，显然m点位于啮合线上。

图6 啮合过程中的坐标变换

设点k1为直线外齿轮齿廓上的任意一点，其在坐标系O1X1Y1中的坐标为（x1，y1）。齿廓在k1处的法线与外齿轮的节圆交于点P1。如果k1要成为接触点，须将外齿轮相对于初始位置逆时针地转过角度φ1，使点P1与节点P重合，这时点k1在固定坐标系O1XY中对应的位置k（x，y）即为啮合线上对应点的坐标。

图6中：

而

为求得啮合线上对应点的坐标，k1点的旋转变换为：

直线共轭内啮合传动的啮合线形态如图7所示，从齿轮齿根位置开始，啮合线一直比较平直，但是到接近齿轮的齿顶位置，啮合线的弯曲程度加大，与渐开线传动有很大的区别。图7中ψ为一对轮齿从进入到退出啮合时外齿轮转过的角度，如果增加外齿轮齿顶圆半径ra1，轮齿之间本来应该结束的啮合过程将由于啮合线的弯曲而大大延长。

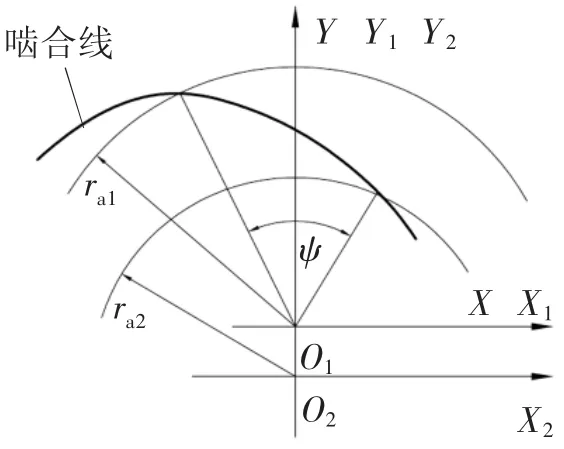
图7 直线共轭内啮合的啮合线

图8是啮合过程中，直线齿廓外齿轮齿轮齿高与对应的啮合转角之间的关系曲线，在靠近齿顶位置曲线开始向上偏转，也说明靠近齿顶位置的轮齿高度，对重合度的贡献相对于齿根部分齿廓要大。

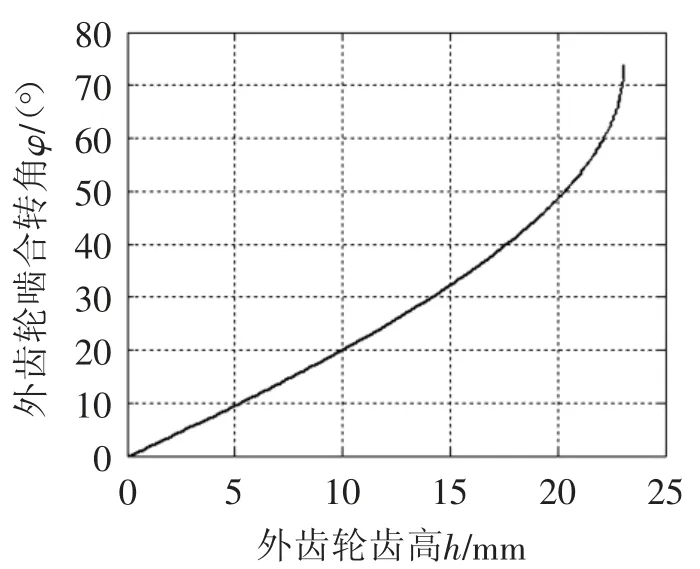
图8 齿轮啮合转角角度与齿高的关系

直线共轭内啮合传动的这种特性，对齿形设计的意义在于，从满足传动重合度要求出发，当工作齿面在直线BC 靠近齿根段时，需要的齿高要大一些，如此设计的齿轮副，在内啮合齿轮泵中可以得到比较大的排量而避免出现困油现象；而如果工作齿面在直线BC靠近齿顶段，用比较小的齿高就可以满足连续传动的要求，从而可以在行星传动中采用短齿来解决内啮合传动的干涉问题，同时提高轮齿弯曲强度。

另外，在整个啮合过程中，啮合点在齿面上移动速度变化也比较大，而靠近齿顶时，啮合点的位置变化相对较慢，对于齿轮泵中的内啮合齿轮副，可以利用这个特性来控制啮合点位置，减小输出流量脉动。总之，相对于渐开线齿轮，直线共轭内啮合传动的齿形参数设计有更大的灵活性来适应不同传动工况要求。

5 重合度

齿轮传动的重合度分析需要计算一对轮齿从进入啮合到退出啮合过程中，齿轮转过的角度，对于齿形参数设计，重合度主要取决于外齿轮和内齿轮的齿顶圆大小。

根据图9中直线共轭内啮合齿轮副之间的几何关系，啮合点k到外齿轮中心O1的距离为

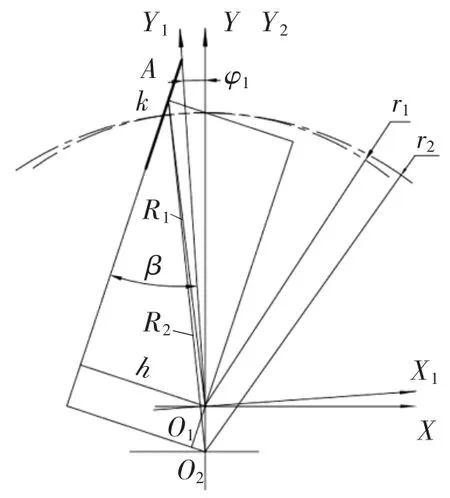
图9 直线共轭内啮合齿轮副重合度计算

式中：ψ1为从初始位置开始，外齿轮的转角，h为直线齿廓到外齿轮中心的垂直距离，计算公式为

啮合点到内齿轮中心O2的距离为

齿轮副开始啮合时，有

式中，ra2为内齿轮齿顶圆半径。

而啮合终了，外齿轮的齿顶退出啮合时，有

分别将式（27）、式（28）代入式（24）、式（26），可求得一对轮齿进入和退出啮合时外齿轮的转角，进而计算出齿轮传动的重合度。

6 工程运用实例

为了验证本文的研究结果，取一对内啮合齿轮泵中使用的渐开线内啮合齿轮副，用直线共轭内啮合齿形重新设计齿轮参数，保持齿轮的中心距离及齿顶圆半径相同,两种齿轮副的参数对照如表1所示。为了保证互换性，两对齿轮副的齿轮的齿轮圆、齿根圆和中心距相同，计算结果表明两种齿形的齿轮副的主要齿形参数接近，但在啮合过程中的压力角变化规律有较大差别。

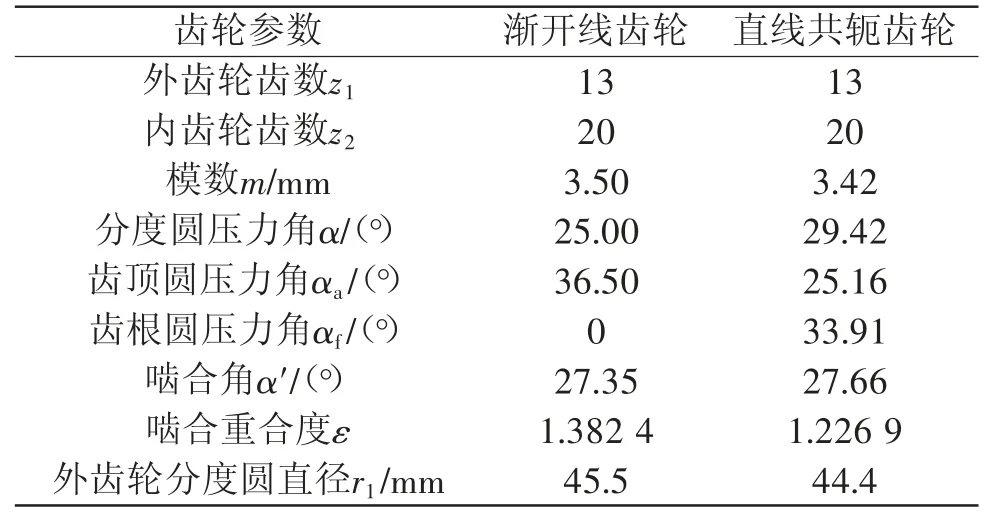
表1 齿轮参数对照表

图10为新旧齿形零件的对比照片，经过试验测试，直线共轭齿形的齿轮副在原渐开线内啮合齿轮泵中工作情况良好。

图10 两种齿形齿轮零件的对照

7 结论

1）在直线共轭内啮合齿轮传动中，直线齿廓外齿轮的压力角取决于齿顶半角和齿数；齿顶半角越大，齿数越少，压力角越大；对于给定的压力角，存在一个最小齿数。另外，压力角随啮合点半径的增大而减小，最小压力角等于齿顶半角。

2）直线齿廓外齿轮存在上下啮合极限点，而齿顶的啮合极限点有可能小于齿顶圆，造成部分齿廓不能参与啮合，以及出现干涉现象。

3）直线齿廓外齿轮可以与一个共轭的内齿轮构成内啮合传动，内齿轮的齿廓曲线与中心距有关，其啮合线为一条曲线，啮合线在接近齿轮的齿顶位置弯曲程度加大，靠近齿顶位置的轮齿高度，对重合度的贡献相对于齿根部分要大得多。

直线共轭内啮合齿轮副加工并不困难，外齿轮类似于三角形外花键，可以在铣床或滚齿机上加工，并利用花键磨床磨削；内齿轮的加工，大批量生产采用拉削技术，生产效率高，精度容易保证，小批量加工也可以采用插齿。可以预见，随着直线共轭内啮合传动理论研究的深入，这种齿轮传动方式不但可以在内啮合齿轮泵中得到更好的运用，还有可能在行星齿轮传动等领域得到推广。