基于萤火虫-遗传算法的机械臂轨迹时间优化
2024-02-27李甚霖曾庆生冯栋彦夏广健
李甚霖,曾庆生,冯栋彦,夏广健
(南华大学机械工程学院,湖南 衡阳 421001)
0 引言
随着科学技术的迅速发展,工业生产正逐步走向自动化、智能化。机械臂是实现智能生产的有力工具,在焊接[1]、搬运[2]、机械加工[3]等方面已得到广泛的应用。在实际应用中,为提高工作效率,往往需要对机械臂的运行轨迹进行优化。目前国内外学者和专家主要是以时间优化[4]、能量优化[5]、冲击优化[6]和综合优化[7]为目标展开研究,其中时间优化是研究和探讨的热门方向。
轨迹时间优化是在满足机械臂约束条件的情况下尽可能地缩短运行时间,以提高机械臂工作效率。由于其计算量大、计算复杂,一般使用智能算法来进行优化。常用的智能算法有粒子群算法、遗传算法、萤火虫算法等。居鹤华等[8]使用3-5-3样条函数进行轨迹规划,在速度约束下,使用遗传算法求解最优时间。Liu等[9]使用五次多项式规划轨迹,在遗传算法中引入精英保留策略和自适应机制来优化轨迹时间。郭鑫鑫等[10]使用3-5-3插值函数规划机械臂轨迹,改进萤火虫算法来优化轨迹。
基于以上研究,本文使用五次多项式进行机械臂末端轨迹规划,将精英保留遗传算法与萤火虫算法结合,提出一种萤火虫-遗传算法,以加强遗传算法局部搜索能力。使用此算法在运动学约束下优化轨迹的运行时间。使用MATLAB进行仿真实验验证该方法的有效性。
1 机械臂运动学分析
AUBO-i10是遨博公司研发的轻型6自由度协作机械臂,具有体积小、灵活度高的特点,其实物如图1(a)所示。对机械臂进行运动学分析,需建立其运动学模型。首先建立机械臂各个关节的坐标系,如图1(b)所示,采用改进型D-H参数法[11]建立各关节的坐标系。坐标系0为世界坐标系,坐标系1~6为关节1~6的坐标系。坐标系1~6的Z轴方向为各关节轴线方向;坐标系1、4、5和6的X轴方向分别为垂直于Z1和Z2、Z4和Z5、Z5和Z6方向,坐标系2、3的X轴方向为连杆方向。
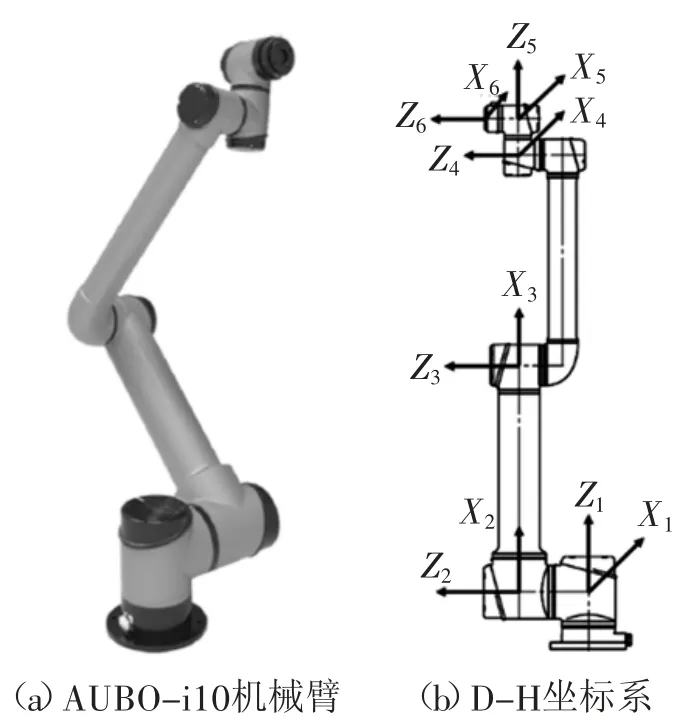
图1 AUBO-i10机械臂及其D-H坐标系
建立坐标系后即可得到机械臂的改进型DH参数,如表1所示。
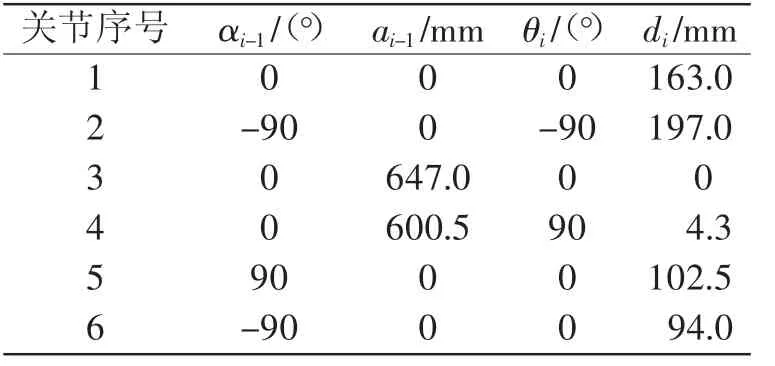
表1 A UBO-i10机械臂D-H参数表(改进型)
表1中:αi-1为机械臂连杆扭转角,ai-1为连杆长度,di为连杆偏距,θi为关节转角。
为进行机械臂末端轨迹规划,需知道机械臂基座坐标系到末端坐标系的变换关系,即坐标系变换矩阵。设第i-1个坐标系变换到第i个坐标系的变换矩阵为,则有
式中:C=cos,S=sin。
2 轨迹规划
按轨迹所在空间可将轨迹规划分为关节空间轨迹规划和笛卡尔空间轨迹规划。笛卡尔空间轨迹规划可以直接按照用户指定的路径点进行规划,但是运行时必须以实时更新的轨迹速度求出运动学逆解,计算量很大。关节空间的规划方法非常便于计算,并且由于关节空间与直角坐标空间之间并不存在连续的对应关系,因而不会发生机构的奇异性问题[12]。因此本文选择在关节空间进行轨迹规划。
关节空间轨迹规划常用的方法有三次多项式插值、五次多项式插值、多段多项式组合插值、B样条曲线、NURBUS曲线等[13]。机械臂工作时的轨迹一般为点到点,由已有信息可知初始点和目标点的关节位置、速度,为减小机械臂的振动与冲击,对关节加速度施加约束,指定初始点和目标点的加速度,则共有6个约束条件,因此采用五次多项式进行轨迹规划。五次多项式表达式为
对θ(t)求一阶导数、二阶导数可以得到机械臂末端的速度、加速度多项式表达式:
由已知信息可知多项式的约束条件为:
将式(2)~式(4)代入式(5)可解得:
3 时间最优轨迹优化
使用五次多项式插值规划所得的轨迹还不是时间最优的轨迹,要实现运行时间最短,还需对轨迹的运行时间进行优化。
3.1 时间优化模型
轨迹运动时间函数为
机械臂末端沿轨迹的运动时间与机械臂关节的运动速度成反比例关系,运动时间越少,则关节角速度、角加速度越大;但现实中机械臂的关节速度、加速度是有限的,为了不对机械臂造成损坏,关节位置、角速度、角加速度不应超过其临界值。即:
3.2 基于萤火虫-遗传算法的轨迹优化
遗传算法最早由美国密执安大学的Holland教授提出,起源于20世纪60年代对自然和人工自适应系统的研究,是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法[14],具有很强的全局搜索能力。
萤火虫算法是剑桥学者Yang[15]受到自然界中萤火虫个体发光会相互吸引的启发而提出的一种元启发式智能优化算法。该算法具有很强的局部搜索能力。
本文在精英保留策略遗传算法的基础上,将萤火虫算法融入其中,使用萤火虫算法进行变异操作,提出一种萤火虫-遗传算法,使用此算法对五次多项式插值所得机械臂末端轨迹进行时间优化。具体算法流程如图2所示。

图2 萤火虫-遗传算法流程图
1)初始化种群。随机生成M个个体组成初始种群,每个个体表示轨迹的运行时间,通过二进制编码方式进行编码,编码长度为20,以保证可行解的精度为0.000 1。
2)适应度评价。为实现式(8)中的机械臂约束条件,使用罚函数对适应度函数进行处理。对不满足约束条件的个体进行惩罚,降低其适应度,使其向可行域边界靠近,随着迭代而被剔除掉。
适应度函数为
式中:C为常数,λ为惩罚项。当机械臂关节的角位移、角速度、角加速度满足约束条件时,λ=1,不影响个体的适应度;不满足约束条件时,λ=-1,个体适应度变小。常数C保证受到惩罚的个体适应度不会超过可行域边界。
3)选择精英个体和子代个体。计算种群个体的适应度后将前10个适应度的个体作为精英个体保留,不参与交叉变异,防止优秀个体的基因被破坏。使用随机遍历抽样法选择M-10个个体作为子代进行交叉变异,补充种群数量并保证种群中基因的多样性。
4)使用通常多点交叉法对子代进行交叉操作,以产生新的个体。
5)变异计算交叉操作后子代个体的适应度,与父代种群的平均适应度进行比较,低于父代平均适应度的个体通过萤火虫算法向父代最优个体进行定向变异。具体步骤如下所示:
a.计算萤火虫发光亮度。即计算每个个体的适应度。
b.计算距离。距离计算公式为
式中,xi、xj分别为父代最优个体和子代个体基因解码后的数值,即运行时间t。
c.计算吸引力。一只萤火虫的吸引力计算公式为
式中:β0为常数,表示最大吸引力,通常设置为1,γ为光吸收系数。
d.靠近过程。发光亮度低的萤火虫会被亮度高的萤火虫吸引而向其靠近,即变异。萤火虫更新位置的公式为
式中:α为随机项系数,(rand-0.5)为随机扰动,以便跳出局部最优解。
6)精英个体和子代个体一起组成新的种群。
7)判断是否达到终止条件,未达到终止条件则返回到步骤2),进入下一个循环,达到终止条件则算法结束,输出最优解。
4 仿真实验
4.1 轨迹规划仿真
在MATLAB中使用Robotics Toolbox建立AUBOi10机械臂模型:将改进型D-H参数表中的数据导入Link函数来定义机械臂各个连杆的属性,再使用SerialLink函数定义机械臂各个关节属性,建立的机械臂模型如图3所示。
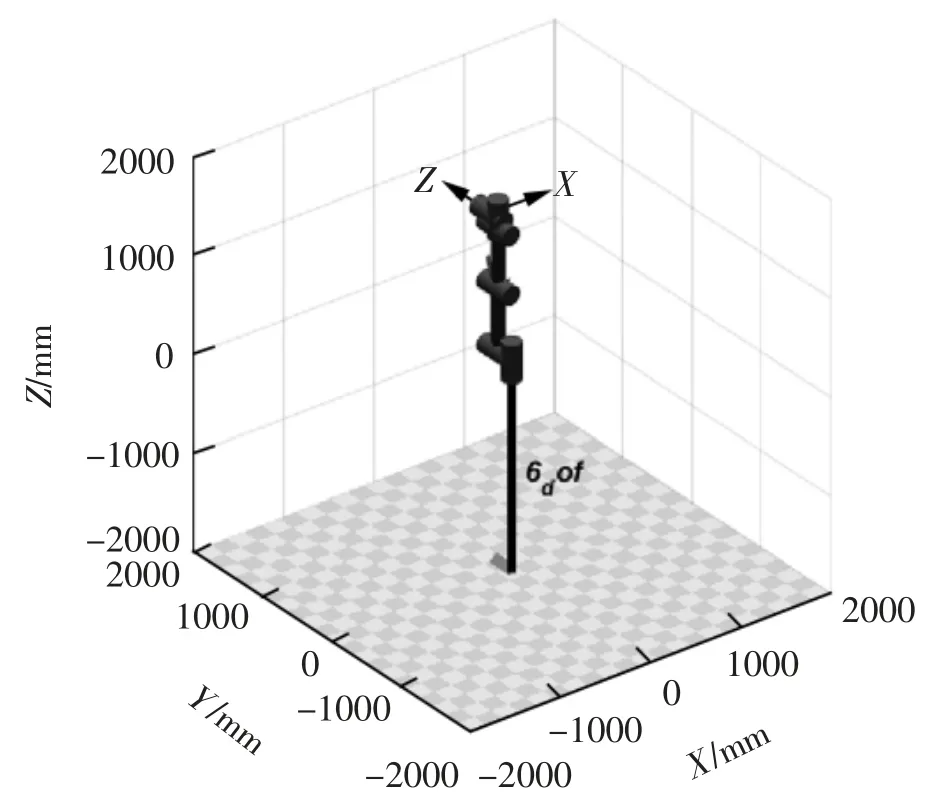
图3 AUBO-i10机械臂模型
设定机械臂起始点坐标为(-100,1000,300),目标点坐标为(600,-700,600),单位为mm。使用jtraj函数获得五次多项式插值的机械臂末端轨迹,如图4所示。
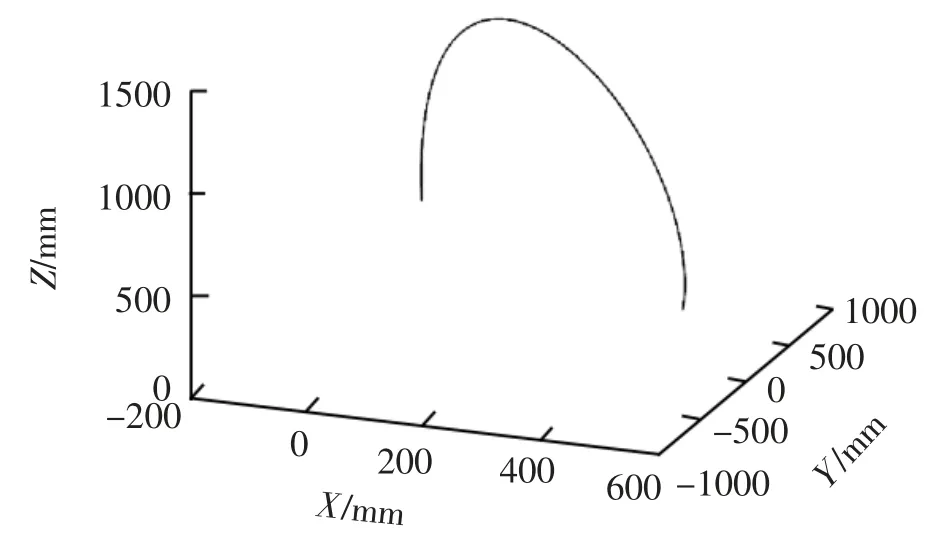
图4 机械臂五次多项式末端轨迹
4.2 时间优化仿真
设定萤火虫-遗传算法的编码长度、进化代数、种群大小、交叉概率、变异概率、运行时间取值范围、光吸收系数和随机项系数分别为20、100、100、0.7、0.01、[0 20]、0.8、0.5。机械臂约束条件如表2所示。

表2 机械臂各关节约束
按照3.2节中的萤火虫-遗传算法流程,分别对机械臂的6个关节进行时间优化。以关节3的优化为例将传统遗传算法、精英策略的遗传算法和萤火虫-遗传算法进行对比,结果如图5所示:传统遗传算法在第70代时收敛至最优解t=2.1411;精英遗传算法在第60代收敛至最优解t=2.0908;萤火虫-遗传算法在第20代收敛至最优解t=2.0908。由此可知,萤火虫-遗传算法具有更好的优化效果。

图5 轨迹时间优化结果
机械臂各个关节在萤火虫-遗传算法优化后得到的运行时间如表3所示。由于机械臂的各个关节在同一时间内完成运动,所以选择其中最大的优化时间,则机械臂轨迹时间优化的结果为t=2.0908。
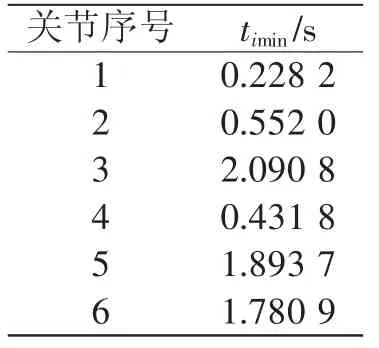
表3 各关节最优时间
将优化后得到的最优时间代入jtraj函数进行五次多项式轨迹规划,得到机械臂各关节的角位移、角速度和角加速度随时间变化的曲线,如图6所示。关节位置、角速度和角加速度曲线光滑连续,且满足表2中的约束条件,验证了算法的有效性。
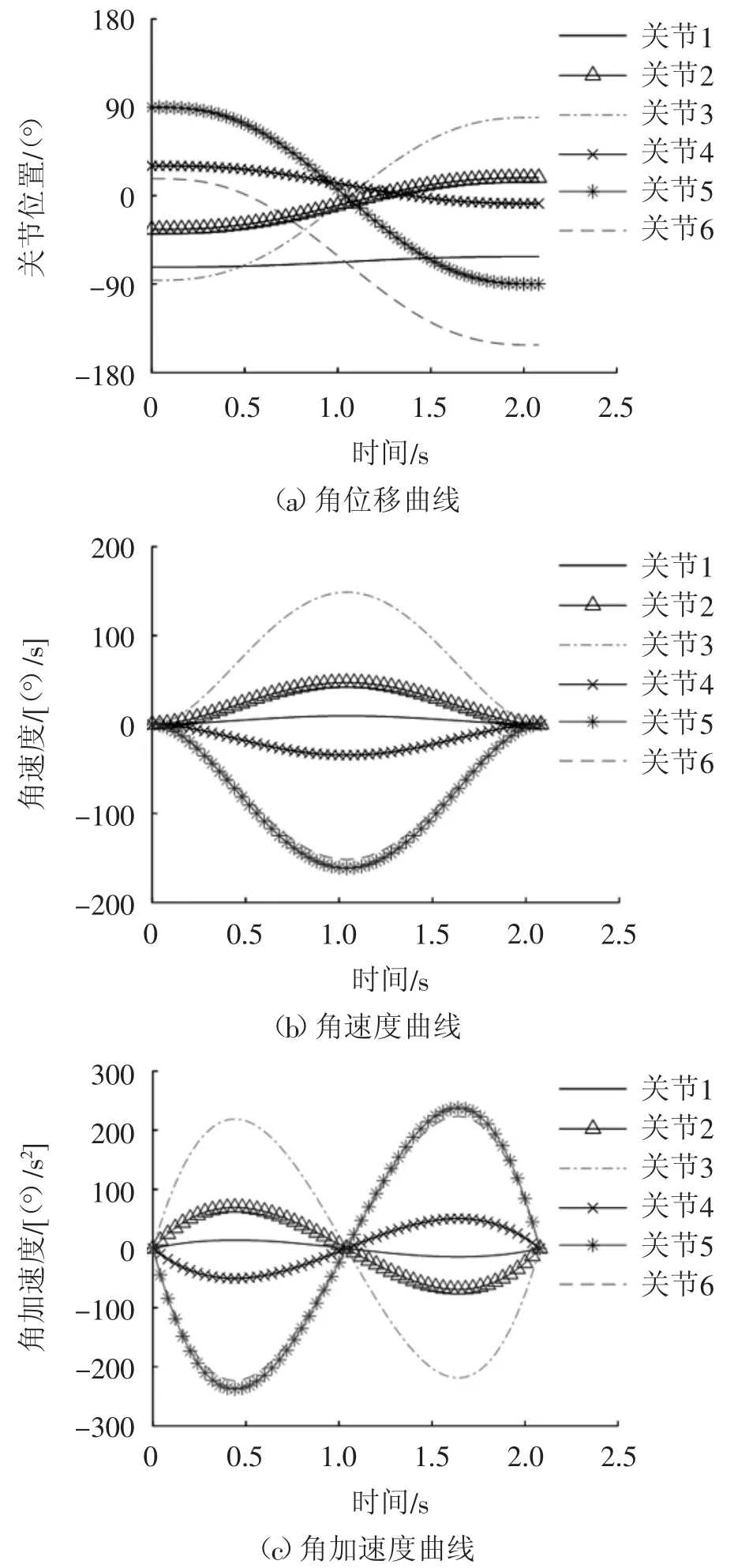
图6 优化后各关节运动曲线
5 结论
1)将萤火虫算法用于遗传算法的变异操作,结合自适应遗传策略,提出了一种萤火虫-遗传算法。在五次多项式规划轨迹的基础上,基于此算法提出了一种机械臂末端轨迹时间的优化方法。
2)使用MATLAB进行仿真实验,最优时间由传统遗传算法的2.141 1 s降低到2.090 8 s,收敛速度也得到大幅提升,验证了该算法的优越性。并将优化后的时间代入轨迹仿真,所得机械臂各关节的角位移、角速度和角加速度曲线连续光滑,且满足机械臂各关节的约束条件,验证了该优化方法的有效性。
