基于海上风力发电机组中虚拟飞轮储能系统的频率支撑协调控制策略
2024-02-27刘泽健魏长春
刘泽健,杨 苹,林 旭,刘 洋,魏长春
(1.广东省绿色能源技术重点实验室(华南理工大学),广东广州 510641;2.深圳华工能源技术有限公司,深圳 518029;3.广东电网有限责任公司电力调度控制中心,广东广州 510600)
0 引言
发展海上风力发电场,构建以风能、太阳能等新能源为主的电力系统,是实现“碳达峰”、“碳中和”的重要途径[1-3]。我国主要海上风能资源集中在东南沿海地带,用电高需求地区也集中在东南沿海地带[4]。因此,大力发展海上风力发电,不仅能够合理利用资源,也可缓解东南地区用电紧张问题[5-6]。
传统电力系统由同步发电机供电,同步发电机转子惯量可等效为电力系统的惯量。当电力系统频率出现波动后,同步发电机的转子能够通过吸收和释放能量来抑制频率波动[7]。由于海上风力发电机组(Offshore Wind Turbines,OWTs)通过网侧变换器(Grid Side Converter,GSC)接入电网,无法通过转子吸收和释放能量来抑制频率波动,导致电力系统的等效惯量被削弱[8-9]。
OWTs 通常工作于最大功率跟踪模式,其输出功率受风速影响具有波动性和随机性[10-11],因此OWTs 通常不具备调频能力。传统海上风力发电场并入电网时采用下垂控制或虚拟惯量控制[11],下垂控制依靠频率参考值与当前值的偏差控制输出功率[12],虚拟惯量控制依靠电网频率的变化率控制输出功率[13-14]。文献[15]研究一种基于虚拟飞轮储能系统(Virtual Flywheel Energy Storage System,VFESS)的OWTs 控制方式,可释放和吸收能量。通过VFESS 释放和吸收能量,可抑制由新能源发电功率、负荷功率的波动性导致的电力系统功率不平衡问题,进而可抑制电力系统短时频率波动。
火力发电场调节频率的缺点是时间长,当电网出现功率缺额导致频率跌落后,将启动低频减载设备减小系统负荷,进而影响负荷端供电稳定性[16-17]。OWTs 可提供短暂的频率支撑,避免低频减载设备频繁动作。但是VFESS 容量较小,能够吸收、释放的能量有限,采用传统下垂控制策略控制VFESS时,未对VFESS 的输出功率曲线进行优化,影响OWTs 短时频率支撑的性能。据此,本文提出基于OWTs 中VFESS 的频率协调控制策略,并利用遗传算法优化VFESS 吸收和释放功率曲线,以实现电力系统频率跌落最小、频率变化率最小的目的。算例分析表明,本文所提方法可优化VFESS 输出功率曲线,进而降低电力系统频率跌落的幅度,减小低频减载装置动作的次数。
1 系统拓扑结构与数学模型
1.1 系统拓扑结构
海上风力发电场的拓扑结构如图1 所示。其中,包含6 个子风力发电场(以下简称子风电场),每个子风电场包含16 台OWTs。
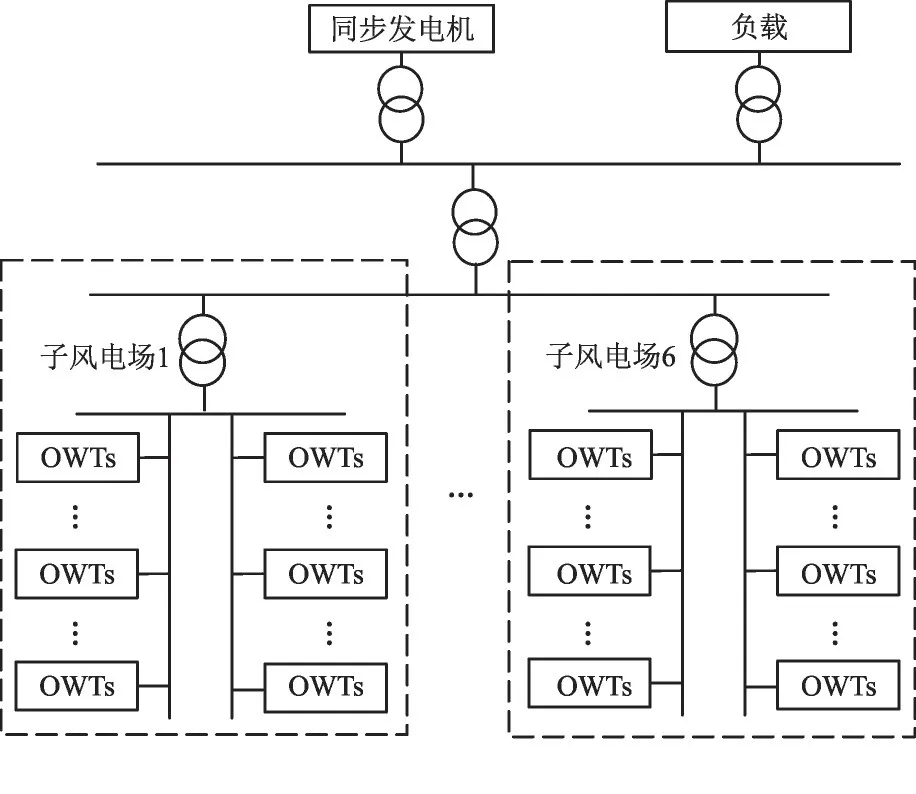
图1 海上风力发电场拓扑结构Fig.1 Topology of offshore wind farms
OWTs 均采用永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)作为发电机、背靠背变换器作为驱动器[18],OWTs 拓扑结构如图2 所示。图2中,分别为子风电场馈线A,B,C 三相电压与电流,L为滤波电感,R为电缆等效电阻,Cdc为直流母线电容,分别为GSC A,B,C 三相输出电压,分别为机侧变换器(Motor Side Converter,MSC)A,B,C 三相输出电压,为直流母线电容电流,O为中性点,G 为风力发电机。
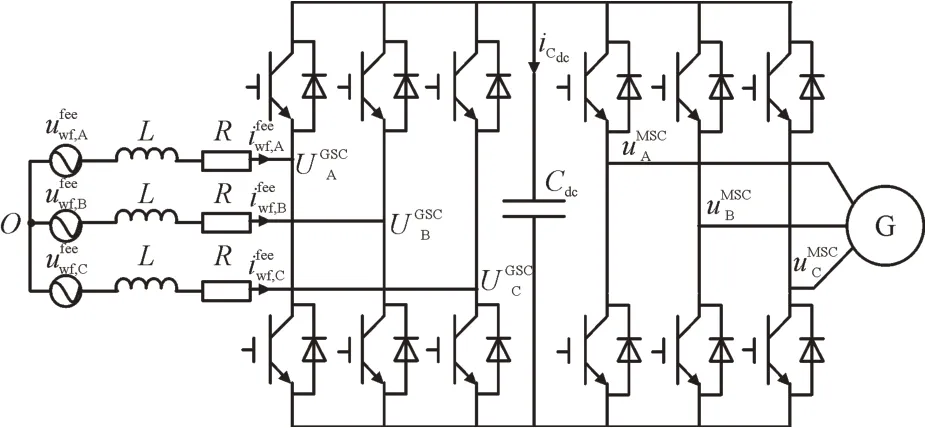
图2 OWTs拓扑结构Fig.2 Topology of OWTs
1.2 MSC数学模型与控制策略
PMSM 采用转子磁链定向的矢量控制时,在两相旋转dq坐标系下的数学模型为[19-20]:
MSC 的控制策略采用功率外环、电流内环的双闭环矢量控制策略,其中控制器采用比例-积分(Proportional Integral,PI)控制器,脉宽调制策略采用空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)策略,MSC 控制策略框图如图3 所示。其中,分别为OWTs 输出功率的参考值和实际值,分别为的参考值,分别为PMSM 的定子绕组A,B,C 三相电流。输出功率参考值根据海上OWTs 所在区域风速确定。

图3 MSC控制策略框图Fig.3 Flowchart of control strategy for MSC
1.3 GSC数学模型与控制策略
GSC 采用基于电网电压定向的矢量控制时,在两相旋转dq坐标系下的数学模型[21-22]为:
GSC 控制策略采用双闭环控制策略,内环为电流环,外环为直流母线电压环与无功功率环,绘制框图如图4 所示。其中,分别为直流母线电压参考值与实际值,分别为与的参考值,分别为子风电场GSC输出无功功率参考值与实际值。
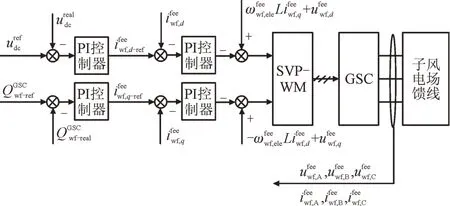
图4 GSC控制策略框图Fig.4 Flowchart of control strategy for GSC
1.4 桨距角控制系统
当风速较高时,需通过控制桨距角改变风能利用系数[23],控制器采用比例-积分-微分(Proportion Integration Differentiation,PID)控制器,桨距角控制框图如图5 所示。其中,βmax,βmin,βref,βreal分别为桨距角最大值、最小值、参考值与实际值,分别为OWTs 的最大角速度、实际角速度与实际角速度差值。
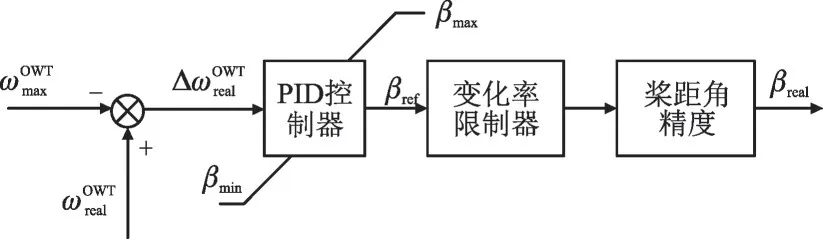
图5 桨距角控制框图Fig.5 Flowchart of pitch angle control
由图5 可知,当风速高于海上OWTs 的额定风速时,可通过桨距角减小风轮功率,降低风能利用系数。即通过控制桨距角使OWTs 运行在宽速度范围,保持恒功率输出。OWTs 的转速变化,可储存机械能形成VFESS,以提供电网的短时频率支撑。
2 风力发电系统与同步发电机协调控制
2.1 场景分析
电网突发负荷扰动的时间可通过智能算法预测,也可通过费控设备进行控制[24]。负荷扰动可分为3 种情况:(1)VFESS 能量不足、负荷扰动持续时间长;(2)VFESS 能量不足、负荷扰动持续时间短;(3)VFESS 能量充足、负荷扰动持续时间短。
由于同步发电机调频时间常数比VFESS 调节频率大。在第1 种情况下,VFESS 存储的能量耗尽,但同步发电机还未动作,此时频率变化曲线如图6 所示。其中,t1为出现负荷扰动的时间,t2为VFESS 储存能量耗尽的时间。
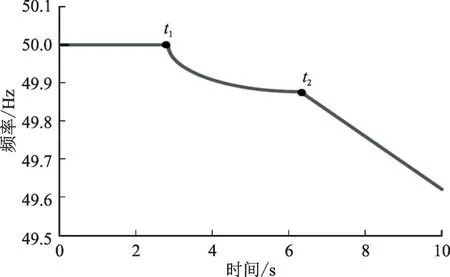
图6 第1种情况下频率变化曲线Fig.6 Frequency variation curve under condition 1
由图6 可知,t1时出现负荷扰动,系统频率跌落;t1—t2时VFESS 输出功率增加,存储能量减小,同时同步发电机也在进行频率调节;t2时VFESS 能量耗尽,但负荷扰动仍然存在,因此频率持续跌落。
第2 种情况下,虽然同步发电机调频时间常数大,但此时负荷扰动消失,因此频率不再跌落维持稳定,频率变化曲线如图7 所示。其中,t3为负荷扰动消失的时间。
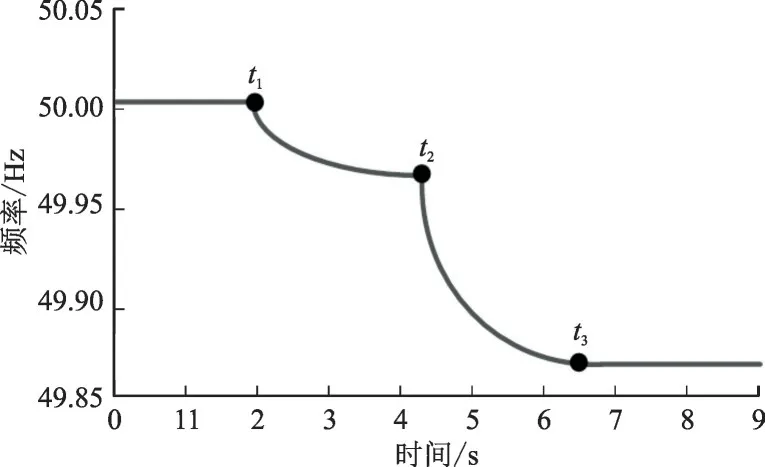
图7 第2种情况下频率变化曲线Fig.7 Frequency variation curve under condition 2
由图7 可知,0-t2时,频率跌落的过程与第1种情况一致;而t2-t3时,VFESS 能量耗尽,退出调频,此时频率持续跌落;t3时由于负荷扰动消失,频率维持稳定。
第3 种情况下,负荷扰动持续时间短,VFESS存储容量大,其频率变化曲线如图8 所示。其中,t4为同步发电机组参与调频的时刻。

图8 第3种情况频率变化曲线Fig.8 Frequency variation curve under condition 3
由图8 可知,t1时发生负荷扰动,系统频率开始跌落,此时VFESS 进行调频,频率跌落较为缓慢;t4时同步发电机组开始参与调频,频率开始恢复;t2时VFESS 能量耗尽,此时仅同步发电机参与调频,系统频率重新跌落,然后缓慢恢复。
综合分析图6—图8 可知,同步发电机虽然能够提供长期的频率支撑,但是动态响应慢、调节时间长。VFESS 的等效惯量比同步发电机的等效惯量小,VFESS 调节频率的时间常数与同步发电机调节频率的时间常数也不同,且VFESS 存储的能量有限,即VFESS 能提供快速的短时频率支撑。VFESS输出功率曲线与其参与调频的时间段长度有关,即其调频性能与其输出功率曲线息息相关,对VFESS输出功率进行优化能够改善其调节频率性能,可实现系统频率最优控制。
2.2 VFESS与同步发电机协调控制
2.2.1 优化目标
在第1 种情况下,优化目标是系统频率差值尽可能小,优化目标函数D1的表达式为:
式中:Δfg为电网频率的差值;t为时间。
在第2 种情况下,优化目标是频率最终点最接近基波频率且频率变化率较小,优化目标函数D2表达式为:
式中:fg-ref,fg-real分别为电网频率参考值与实际值;fg-fin为负荷扰动消失后,电网最终稳定的频率。
在第3 种情况下,优化目标D3是频率最低点最接近基波频率且频率变化率较小,其表达式为:
式中:fg-min为电网最小频率。
2.2.2 约束条件
1)系统功率实时平衡约束为:
式中:ΔPVFE为VFESS 输出功率差值;ΔPsg为同步发电机输出功率增额;为负荷扰动功率。
2)VFESS 的输出能量约束为:
式中:EVFE_max为VFESS 存储的最大能量。
3)OWTs 输出功率约束为:
4)电力系统的频率约束为:
式中:ft为t时电力系统的频率;f0为负荷扰动发生前的频率;Δf∞为起始频率与最终稳态时频率差值;为电力系统频率下降的时间常数;ΔP为电力系统功率缺额;PK为单位调节功率;Jsg为同步发电机组的转动惯量。
3 基于遗传算法的目标函数求解
遗传算法是一种全局优化算法,通过对种群进行选择、交叉、变异等操作产生新的种群,逐步进化种群到最优解[25-27]。最优VFESS 输出功率曲线P(t)采用多项式函数进行拟合,其表达式为:
式中:a1,a2,a3,a4,a5,a6为多项式函数的系数,可通过遗传算法对其进行优化。
利用遗传算法优化系数时,首先初始化规模N为100 的种群,种群中每1 个个体表示1 组系数。种群中的每1 个个体都能够得到对应的VFESS 输出功率曲线,然后将该曲线作为实际VFESS 的输入信号,得到电力系统的频率曲线,结合式(3)—式(5)可获得该个体的适应度。
遗传算法进行种群遗传进化时,为了保障子代遗传优良基因,将适应度高于平均适应度且交叉概率大的个体视为优良个体。为了保障子代改善劣势基因,将适应度低于平均适应度且变异概率大的个体视为劣势个体。即通过交叉遗传优良个体的基因,通过变异改善劣势个体的基因,达到进化种群的目的。个体交叉概率prc和变异概率prm的表达式为:
式中:bmax,bmin分别为群体中所有个体适应度的最大值、最小值;b′,b″分别为2 个交叉个体中较大适应度、较小适应度,为种群平均适应度,b为个体适应度;nprc1,nprc2分别为个体交叉概率参数,设置为0.9 与0.2;nprm1,nprm2分别为个体变异概率参数,设置为0.3 与0.8。
4 算例分析
为验证本文提出的海上OWTs 主动支撑频率策略的有效性,搭建了仿真模型。具体参数如下:交流侧电感为0.04 mH,VFESS 存储能量为1 MJ,负荷扰动为4 MW,负荷扰动出现时间为第8 s,同步发电机组的转子惯性时间常数(标幺值)设置为47.28 p.u.。
4.1 VFESS支撑频率
在第1 种情况下,利用遗传算法求解目标函数式(4),得到VFESS 输出功率参考值,并仿真获得本文所提协调控制策略与传统下垂控制策略下系统的频率实际值对比结果。其波形如图9 所示。
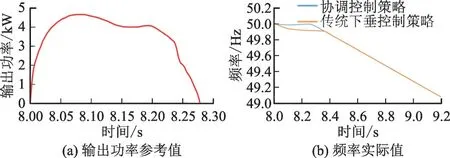
图9 第1种情况下系统输出功率参考值与频率实际值的波形Fig.9 Waveforms for output power reference value and frequency actual value under condition 1
由图9 可知,由于此时假设同步发电机组并未参与调频,因此频率下降已经超出了相关规章制度规定的下降速率。出现负载扰动时,采用协调控制策略时VFESS 存储能量在8.27 s 左右耗尽。而传统的下垂控制在8.36 s 左右能量耗尽。但采用传统下垂控制策略,在出现负荷扰动初期,电力系统频率跌落幅度比采用协调控制策略时的频率跌落幅度大。即在第8 s 扰动初期,通过优化VFESS 的输出功率,能够抑制频率跌落幅度。但VFSS 存在存储能量少、负荷扰动时间长的缺点,当VFESS 存储的能量释放完毕时,电力系统的频率将加速跌落,最终与采用下垂控制策略时的电力系统频率一致。
在第2 种情况下,设负荷扰动存在时间为0.4 s时,协调控制策略与传统下垂控制策略下电力系统频率波形如图10 所示。
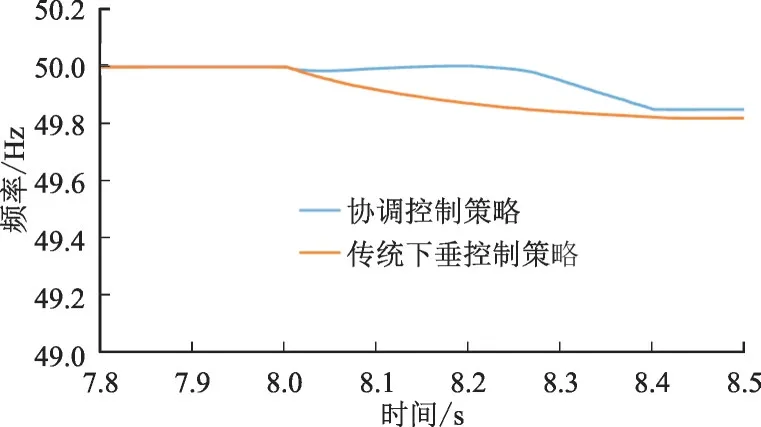
图10 第2种情况下电力系统频率波形Fig.10 Waveforms for power system frequency under condition 2
由图10 可知,采用协调控制策略的频率最小值比采用传统下垂控制的频率最小值更接近50 Hz。且在负荷扰动刚发生时,采用协调控制策略的频率变化率比采用传统下垂控制的频率变化率小。采用协调控制策略时,当VFESS 能量耗尽后电力系统频率下降较快,但是最终频率仍然更接近频率参考值。
4.2 VFESS与同步发电机共同支撑频率
当同步发电机参与调频时,需考虑响应时间的滞后性。采用协调控制与传统下垂控制策略时,得到电力系统频率与VFESS 输出功率的仿真结果如图11 所示。

图11 协调控制与传统下垂控制策略的仿真结果Fig.11 Simulation results of coordinate control strategy and tradition droop control strategy
由图11 可知,采用协调控制策略时,电力系统的频率最小值更接近50 Hz,且频率跌落较为缓慢。即通过VFESS 存储的能量,能够实现短暂的频率支撑,减小电力系统的频率跌落,有效避免了系统低频保护装置动作。
5 结语
本文针对海上风力发电场并入电网导致电网等效惯量下降问题,提出基于OWTs 中VFESS 的频率支撑协调控制策略,并利用遗传算法优化VFESS吸收和释放功率的曲线。OWTs 能够通过控制转速工作在一定范围内构成VFESS,实现短暂的频率支撑。当电力系统出现负荷扰动并存在频率波动时,可通过遗传算法优化VFESS 的输出功率,进而按照寻优出的最优VFESS 输出功率控制VFESS。算例分析表明,本文所提方法能够有效的提高电力系统频率最低点,提高电力系统稳定性,避免低频保护装置保护。
