基于暂态特征参数的数字式非接触负载测量研究

朱正斌 （中国电源学会学生会员），黄 军，牛剑锋，孟洋洋，胡斯登

（1.浙江大学电气工程学院，杭州 310000；2.上海空间电源研究所，上海 201109）

磁耦合式的无线能量传输WPT（wireless power transmission）技术不断发展，其通过电磁感应的方式将能量非接触地从电源端传递到负载端，具有安全、便利和灵活等优点，在电动汽车充电、航空航天及植入式生物医学等不方便或不可能直接接触的场景中得到了广泛应用[1]。在一个WPT 系统中，二次侧负载可通过电磁耦合改变整个系统的阻抗，影响系统控制和能量传输效率。因此，负载的测量与辨识是WPT 系统高效率、高性能稳定运行的重要基础，快速准确地辨识和测量负载成为研究热点[2-4]。

近年来，通过暂态过程提取负载参数成为该领域研究的新思路，基于零输入响应中的暂态过程，通过分析电压或电流信号的幅值衰减率，计算出待测负载的阻值，实现了大阻值负载的高精确度测量[5-6]。然而负载阻值较小时，上述测量方法的精度明显降低。针对此问题，文献[7-8]分析认为，负载电阻减小后，WPT 系统的暂态过程将由二阶系统的暂态响应过渡到四阶系统的暂态响应，暂态行为随之发生变化，测量精度降低，因此，该文献采用二极管包络检波电路滤除四阶振荡波形的拍频，实现了小阻值负载的精准辨识。

文献[10]讨论了同步检波，一种基于双差分放大电路的小信号线性检波方法，有效解决了二极管包络检波中出现的检波精度低以及二极管产生的非线性压降问题，但该方法需要准确判断载波信号的相位，相位不同步会造成检波信号失真；文献[11-12]介绍了一种基于希尔伯特变换（Hilbert transform）的数字包络检波方法，通过设计一个90°移相器，实现信号频谱各分量幅值不变的同时相移90°，进而获取信号包络线，相比于前述包络检波方法，对包络信号的提取更加平滑准确。

综上，为了从高阶非线性的WPT 系统中更加准确地提取负载阻值，本文将希尔伯特变换应用到电压信号的数字处理上，取代二极管包络检波的中间环节，精确测量小阻值负载，并在此基础上补充大阻值负载辨识算法。避免了检波器电路参数的设计，简化了系统电路，在保证测量精度的同时进一步拓宽了非接触负载测量系统的阻值辨识范围，即其通用性更强，对大阻值负载或小阻值负载，均能够精准测量。最后，通过仿真和实验对所提方法的有效性进行验证，同时，将测量对象扩展到电池内阻，为无人机等飞行器电池内阻的测量提供新思路。

1 基于暂态特征参数的非接触负载测量原理介绍

图1（a）给出了基于暂态特征参数的非接触负载测量所用主电路拓扑，系统先后进入高频能量注入模式和衰减模式[5-6]，负载电阻的阻尼将通过电磁耦合影响原边侧电压幅值的衰减率，如图1（b）所示。因此测量衰减模式暂态过程中电感线圈两端电压，提取振幅衰减率即可实现对负载阻值的测量。

图1 非接触测量主电路与衰减模式等效拓扑Fig.1 Main circuit topology for contactless measurement and equivalent topology in attenuation mode

图1（b）中等效电路为四阶系统，文献[9]从根轨迹的角度对负载条件与衰减模式进行建模分析，指出在不同负载条件下，系统的暂态过程可能会呈现二阶或四阶阻尼振荡状态。负载条件可表示为

式中：R*为待测负载；和分别为原、副边杂散电阻；L 为原、副边自感平均值；C 为谐振电容；k 为原、副边耦合系数。

当负载阻值较大且满足式（1）时，系统存在主导极点，暂态振荡过程表现为二阶阻尼振荡，如图2（a）所示，且负载阻值越大，主导极点作用越明显，该范围负载阻值的集合定义为K 域；当负载阻值不满足式（1）时，不存在主导极点，暂态振荡过程表现为四阶阻尼振荡，如图2（b）所示，且负载阻值越小，各极点越接近，该范围负载阻值的集合定义为H 域。

不用想我都知道是林全，是他从黄玲那里拿到了我的号码。可是这半夜发短信，又是什么意思？我知道他那天留宿在黄玲这里，也就是我的隔壁。我迅速将短信删掉，像是做贼一般，又觉自己委屈，怎可将自己推到这般境地？

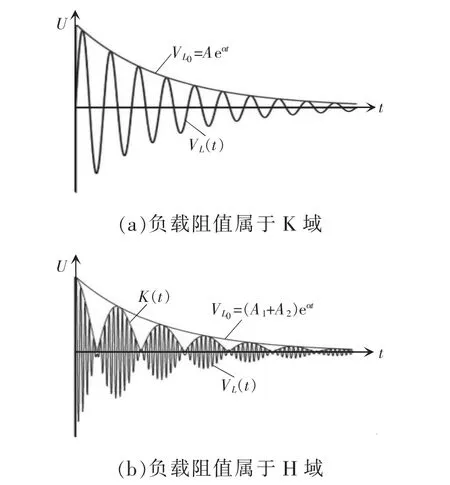
图2 处于K 域和H 域时的电感电压波形及包络线Fig.2 Waveforms and envelopes of inductance voltage in K and H regions

图2（a）为K 域负载的电压响应波形，VL（t）为衰减的原边侧电感电压，为电感电压包络线，则该包络线的衰减率α 与待测负载电阻R*的关系为

式中：M 为原、副边间的互感；ω0为WPT 系统原、副边LC 谐振的固有频率。

图2（b）为H 域负载的拍频电压波形，VL（t）为衰减的原边侧电感电压，K（t）为电感电压的包络线，文献[10]指出VL（t）和K（t）的数学形式为

式中：A 为描述幅值的常量；ωd和ωc为描述频率的常量；t 为时间；φ1和φ2为描述相位的常量。

通过连接拍频的峰值即可获得包络线峰值衰减曲线VL0，其衰减率α 与待测负载电阻R*的关系为

由此，即可通过式（2）、式（5）和电感电压包络线的衰减率α 求解出负载阻值。在现有文献中，电压包络线衰减率的获取大多采用二极管包络检波的方法，其与数字包络检波方法的比较如表1 所示。

表1 模拟电路检波与数字算法检波的对比Tab.1 Comparison between analog circuit and digital detections

数字算法检波的难点在于合适的算法选择，针对非接触负载测量，本文提出了一种基于希尔伯特变换的包络检波算法，主动识别K 域和H 域负载，负载大范围变动时，亦可准确提取包络线，有利于高灵活、宽范围地测量负载参数。

2 基于希尔伯特变换的数字式非接触负载测量

2.1 基于希尔伯特变换的检波算法原理

待处理的电感电压VL（t）为频率固定、幅值逐渐衰减的二阶或者四阶振荡，其包络线刻画了幅值的变化，而希尔伯特变换具有频谱各分量幅值不变的同时相移90°的性质，可低失真地获取非接触负载测量中的电压包络线，便于求取衰减率。本文以四阶振荡时的电感电压VL（t）为例，介绍非接触负载测量中，基于希尔伯特变换的数字检波算法的原理。

为表达方便，以连续时间实值信号ux（t）代指电感电压VL（t），其希尔伯特变换结果uy（t）可以视为ux（t）与冲激响应h（t）=1/（πt）的卷积，则

式中：T[ ]为希尔伯特变换；*为卷积运算；τ 为积分变量。对h（t）做傅里叶变换，可以得到

式中：sgn（）为符号函数；j 为虚数。设UX（ω）和UY（ω）分别为ux（t）和uy（t）的傅里叶变换，则由式（6）及时域卷积定理可得

根据式（8）可知，希尔伯特变换结果不会影响信号的幅值，但会将信号的正频率分量乘以-j，即正频率成分移相负90°；同时会将原始信号的负频率分量乘以j，即负频率成分移相正90°。式（3）中的电感电压VL（t）经希尔伯特变换后的uy（t）表达式可表示为

进一步地，在构造ux（t）的希尔伯特变换uy（t）后，将两者按照欧拉公式进行组合，即可得到ux（t）的解析信号uz（t）

对uz（t）求模可得

因此，对包络线信号K（t）的求解可以转化为对模值|uz（t）|的求解。设UZ（ω）是uz（t）的傅里叶变换，考虑式（8）可得

由式（12）可知，所得解析信号UZ（ω）只含有正频率分量，且是原始信号UX（ω）正频率分量的2 倍。

在获得UZ（ω）后，进行反傅里叶变换即可得到解析信号uz（t），需要指出的是uz（t）是包含实部和虚部的复信号。最后，对复信号uz（t）求模，得到待处理拍频电压的包络线信号K（t）。

2.2 数字式非接触测量的实现

在使用DSP 进行系统控制、数据采集和信号处理时，待处理信号不再是连续信号ux（t），而是采样信号序列ux（n），利用快速傅里叶变换得到频域信号UX（k），与前述连续时域推导过程相同，得到解析信号UZ（k），即

其中，k=0，1，2，…，N-1 且k=N/2，…，N-1 对应负频率部分。进一步地，对解析信号UZ（k）作反变换并求取模值，即可得到原始信号ux（n）的包络线|uz（n）|。数字式非接触负载测量流程如图3 所示。

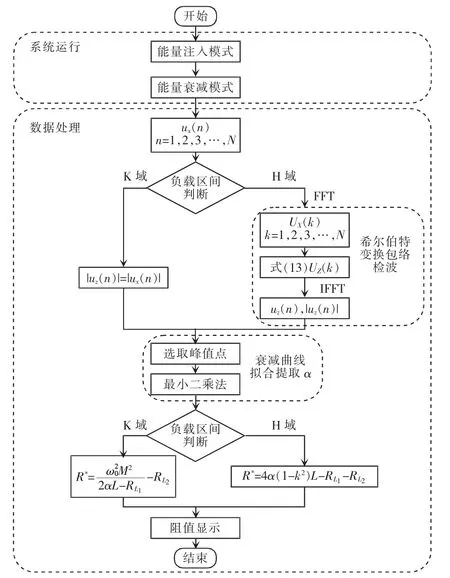
图3 数字式非接触负载测量流程Fig.3 Flow chart of digital contactless load measurement

当系统进入能量衰减模式后，DSP 对电感电压进行数据采样。首先根据振荡波形判断负载区间，若负载阻值位于H 域，则应用希尔伯特检波算法，生成包络曲线；若负载阻值位于K 域，则直接使用振荡波形作为包络曲线。然后选取包络线的峰值点，借助最小二乘法提取衰减率α，最后通过式（2）和式（5）即可计算出负载阻值。

3 仿真及实验结果分析

根据第2 节的分析，设计了基于希尔伯特变换的数字式非接触负载测量平台，并在不同的负载阻值下进行仿真与实验验证，使用的各电路参数如表2 所示。本研究所搭建的实验平台如图4所示，包含WPT 主电路和信号调理电路两部分，其中，主电路中开关器件的控制和电感两端电压信号的数据采集与处理均由德州仪器的TMS320F 28377S 开发板实现，待测电阻阻值为1.11 Ω，其理论阻值由LCR 电桥（型号固纬LCR6100）测量得到。

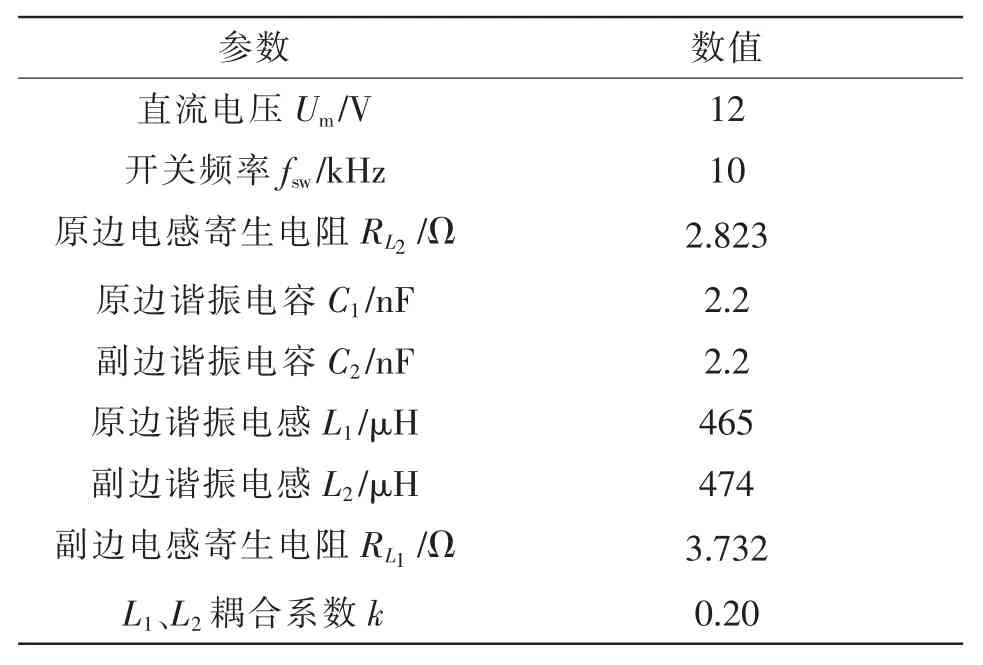
表2 仿真与实验参数Tab.2 Simulation and experimental parameters

图4 实验平台实物Fig.4 Experimental platform

系统能量传输过程结束后，图1（a）所示的开关管S1断开、S2闭合，WPT 系统由高频能量注入模式进入衰减模式。在衰减模式这一暂态过程中，电感线圈两端电压UL不断衰减，其仿真波形如图5 所示。对其进行包络检波，检波的实验和仿真结果如图6所示，其中实验结果为DSP 中读取数据后作图所得，可以看到，数字包络检波器能够准确提取暂态过程中电感电压波形的包络线。

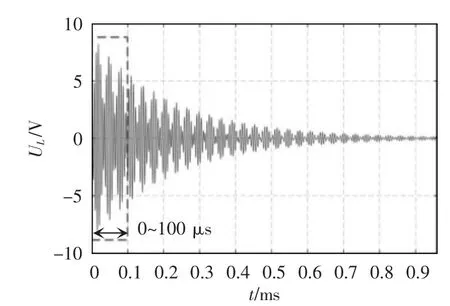
图5 暂态过程电感电压波形Fig.5 Waveform of inductance voltage in transient process

图6 基于希尔伯特变换的数字检波Fig.6 Digital detection based on Hilbert transform

由图6 可见，仿真中，经希尔伯特变换后，拍频电压信号的包络未出现失真，衰减率曲线拟合准确；实验中，由于实际电路中存在信号干扰，包络结果出现略微失真，但在拍频峰值点的包络保真度良好，仍可准确拟合衰减率曲线。

最后，由包络线计算衰减率α 和电阻R*，进行了2 次实验，结果见表3。其中，由于实验电路存在寄生参数，因此实测衰减率α 要比仿真大，实测阻值与理论阻值在误差允许范围内吻合，验证了基于希尔伯特变换的数字包络检波器的可行性。

表3 仿真与实验测量结果Tab.3 Simulation and experimental measurement results

对2 kΩ 及以下多个不同阻值的负载分别进行仿真，对于阻值位于K 域和H 域的负载，辨识误差均小于5%，结果如图7 所示。本研究使用的数字包络检波方法，实现了H 域和K 域系统负载的统一测量，能精确辨识大阻值和小阻值负载。与传统方法相比[7]，该方法在保证H 域系统负载测量精度的同时，减小了K 域系统负载测量的误差，提高了负载精准测量的范围。

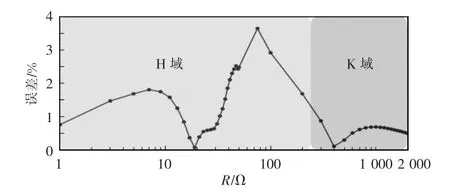
图7 不同阻值负载测量精度和误差结果Fig.7 Results of load measurement accuracy and error with various resistances

进一步地，对电池负载进行多组重复测量，并记录追踪电池放电过程中的阻值变化，如图8 所示。图8（b）中，所提方法多次测量电池内阻的平均值为0.917 Ω，标准差为0.024 Ω，说明该方法在电池内阻测量中同样具有良好的适用性。图8（a）中，电池放电时间越长，内阻越大，且放电前期内阻变化缓慢，这与电池特性一致。因此，本方法可应用于电池内阻的追踪测量领域，为监测电池充放电状态以及健康管理提供了一种有效检测手段。

图8 电池内阻测量Fig.8 Measurement of internal resistance of battery

4 结论

在K 域和H 域中WPT 系统的暂态行为存在差异，而现有模拟包络检波方法参数固定，对不同暂态行为适应性差，导致负载辨识范围窄。针对该问题，本文采用基于希尔伯特变换的数字包络检波方法，并结合K 域和H 域系统特征，优化了WPT系统的暂态特征参数识别与负载测量方法。首先根据负载对电压拍频的暂态影响，利用希尔伯特变换能够精准提取包络线的优势，设计了基于希尔伯特变换的数字包络检波器，实现了小阻值负载的精确辨识，并在此基础上，补充大阻值负载辨识算法，统一了K 域和H 域系统的负载测量方法，与传统方法相比，能够实现全域系统负载的准确测量。最后，本文通过仿真与实验验证了所提方法的有效性。

在负载大范围切换的WPT 系统中，该方法的负载辨识误差小于5%，精确度高，通用性好，同时该方法亦能够实时追踪电池负载内阻的变化，适用于航空航天和汽车电子等多个领域。今后的工作中，会将本研究的成果集成于各类无线充电系统中，辨识智能手机和人体医疗植入设备内嵌电池的内阻，评估电池的安全和寿命。此外还可用于汽车移动式无线充电公路中，在监测汽车电池安全的同时，跟踪和识别汽车位置。