Buck 型单开关整合式功率因数校正变换器

文 娅（中国电源学会学生会员），万宇阳，刘雪山，肖剑桥，王海东

（四川大学电气工程学院，成都 610065）

近年来，随着电力电子技术的快速发展，电力电子装置已经广泛应用于电力系统、工业以及交通等相关领域。为了减小电力电子装置对电网的谐波污染，一些国家和国际学术团体颁布并实施了一些电流谐波标准，如IEC555-2、IEEE519、IEC61000-3-2等[1]。为了满足这些谐波标准，必须使用功率因数校正PFC（power factor correction）技术来使开关变换器的输入电流谐波达到限制标准，因此众学者开始广泛研究各种结构的PFC 变换器。

相比于两级PFC 变换器，单级PFC 变换器具有效率高和体积小的特点[2]，因此，单级PFC 变换器成为人们的研究热点。一般来说，传统的开关变换器拓扑，例如升压（Boost）、降压（Buck）和升降压（Buck-Boost）变换器，都可以实现单级功率因数校正，并且每个拓扑都有各自的特点。

Boost PFC 变换器具有输入电流纹波小和效率高的特点，被广泛应用于PFC 领域[3-4]。在全输入电压（90～265 Vac）范围内，Boost PFC 变换器都可以获得较高的PF 值，尤其当电感电流工作在临界连续模式时，其功率因数为单位1。然而，Boost PFC 变换器只能进行升压转换，即其输出电压必须高于输入电压峰值，这限制了Boost PFC 变换器的应用领域。在全输入电压（90～265 Vac）应用中，该变换器输出的直流电压一般设定为400 V，无法直接给负载设备供电。因此，Boost PFC 变换器一般用于两级变换系统中的前级PFC 变换，后级仍需级联一个降压型DC-DC 变换器。

在全输入电压范围应用中，可兼顾升压和降压转换是一个非常有优势的特性，因此，Buck-Boost PFC 变换器是较好的选择[5-6]。但该变换器的输入电流在一个开关周期内是断续的，因此有较大输入电流纹波，此外，其仅在开关管关断时传递能量给负载，因此相对于Buck 和Boost PFC 变换器，Buck-Boost PFC 变换器的效率较低，开关管电压电流应力高。

Buck PFC 变换器具有可降压转换、开关管应力低和效率高的特点，非常适合非隔离并且输出电压低于输入电压峰值的应用场合[7-9]。然而，该变换器只在输入电压高于输出电压时才会由电源给负载传递能量，也就是说，当输入电压低于输出电压时输入电流为0，输入电流存在死区时间。因此，在全输入电压范围应用中，Buck PFC 变换器的功率因数较低，很难通过各类谐波标准的限制，尤其在输出电压较高的时候。输入并联型变换器可有效改善Buck PFC 变换器的THD，消除输入电流死区。文献[9]研究了一种Buck 变换器与Boost 变换器输入并联工作的PFC 变换器，可实现Buck 模式与Boost 模式的自动切换，但是需要采样输入电压，并且使用了两个主开关管，控制电路复杂。

本文提出了一种Buck 型单开关整合式功率因数校正变换器。该变换器由一个Buck PFC 变换器和一个Buck-Boost PFC 变换器通过一个开关管整合而成，简化了控制；采用恒导通时间控制，消除了Buck PFC 变换器输入电流的死区；结合Buck 和Buck-Boost 变换器的优势，在全输入电压范围下可以实现高功率因数和高效率。因此，所提变换器适用于在全输入电压范围下的PFC 应用场合。本文对该变换器进行了详细地理论分析，并搭建了一台56 W 的实验样机，验证分析结果的正确性。

1 电路结构

为了改善传统Buck PFC 变换器的输入电流谐波，消除输入电流的死区，可以将Buck PFC 变换器和其他变换器整合成一个单开关PFC 变换器，利用此方法，Buck PFC 变换器和其他变换器的开关管导通时间相同。因此，由于其他变换器在输入电压小于输出电压时会继续工作，Buck PFC 变换器的输入电流死区即可被有效消除。图1 为本文提出的Buck 型单开关整合式功率因数校正变换器拓扑及其控制电路，相比于传统的Buck PFC 变换器增加了一个Buck-Boost 励磁电感L1、中间储能电容C1和二极管D2。该PFC 变换器采用恒导通时间控制，其中Buck-Boost 电感电流iL1工作在临界导通模式CRM（critical conduction mode），通过选择L1与L2的电感量，Buck 电感电流iL2工作在频率变化的断续导通模式DCM（discontinuous conduction mode）。相比于传统的定频断续导通模式，变频断续导通模式的电感电流峰值更低，有助于提升变换器的效率。

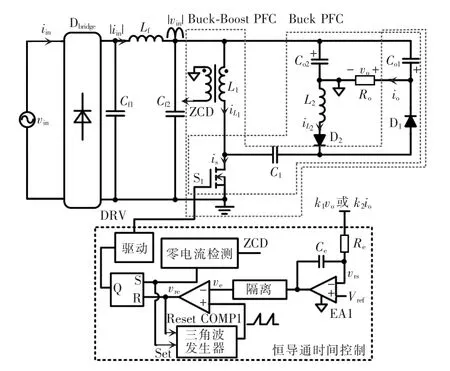
图1 Buck 型单开关整合式功率因数校正变换器及其控制回路Fig.1 Buck-type single-switch integrated PFC converter and its control loop

2 工作原理分析

为了简化分析，做如下假设。

（1）所有的开关管、二极管、电感和电容均为理想元件。

（2）电容C1、Co1和Co2足够大，稳态输出电压的开关纹波可以忽略，即vC1、vo1和vo2为恒定值。

（3）开关频率fs远大于电网电压频率fL，即fs≫fL。

（4）输入电压是全波整流正弦波，即|vin（t）|=Vp|sin（ωt）|，其中Vp为电压幅值，ω=2πfL为输入电压的角频率。

如图2 所示，Buck PFC 变换器仅在输入电压高于vo2-vC1时工作，因此，当所提PFC 变换器工作在稳态时，有2 种不同的工作状态：1）θ＜ωt＜π-θ；2）0＜ωt＜θ 和π-θ＜ωt＜π。其中

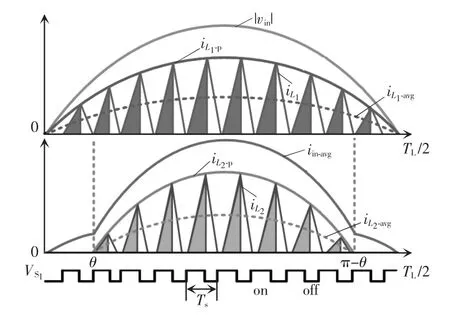
图2 半个工频周期内的输入电流波形及其控制时序Fig.2 Waveforms of input current and its control sequences in a half line cycle

1）θ＜ωt＜π-θ

在此工作状态，所提PFC 变换器在一个开关周期内有3 种工作模态。图3 为其稳态工作时的主要波形，图4 为各模态的等效电路。

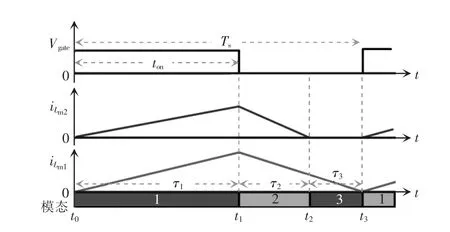
图3 所提单开关整合式PFC 变换器的主要波形Fig.3 Key waveforms of the proposed single-switch integrated PFC converter

模态1 [t0～t1]：如图4（a）所示，在t0时刻，开关管S1导通，输入电源给Buck-Boost 电感L1和Buck电感L2充电，因此，电感电流iL1（t）和iL2（t）线性上升，可表示为

当开关管S1关断时，此工作模态结束，电感电流和达到最大值，即

式中，ton为开关管S1的导通时间。模态1 的工作时间τ1=ton。

模态2 [t1～t2]：如图4（b）所示，在t1时刻，开关管S1关断，此时，电感电流iL1（t）和iL2（t）分别通过二极管D1和D2续流，因此，电感电流iL1（t）和iL2（t）线性下降，可表示为

当iL2（t）下降到0 时，二极管D2关断。在t2时刻模态2 结束，模态2 的工作时间为

模态3 [t2～t3]：如图4（c）所示，在t2时刻，开关管S1和二极管D2都关断，而二极管D1保持导通，电感电流iL1（t）继续下降，在t3时刻，iL1下降到0，二极管D1关断，模态3 结束且一个开关周期完成。模态3 的工作时间为

由式（6）和式（7）可得，所提PFC 变换器一个开关周期为

2）0＜ωt＜θ 和π-θ＜ωt＜π

在此工作状态，所提PFC 变换器在一个开关周期内有2 种工作模态，与传统CRM Buck-Boost PFC 变换器相同，图5 为其为各模态的等效电路。在模态1 时，二极管D2反向截止，电感电流iL2=0，其余工作状态与θ＜ωt＜π-θ 时相同；在模态2 时，工作状态与θ＜ωt＜π-θ 时的模态3 相同。在θ＜ωt＜π-θ情况下，电容Co2存在充电模式和放电模式；在0＜ωt＜θ 和π-θ＜ωt＜π 情况下，电容Co2只存在放电模式。在一个工频周期内，电容Co2可以满足安秒平衡特性。由于电容Co2的容值足够大，为了便于理论分析，假设电容Co2稳态输出电压的开关纹波可以忽略，即vo2为恒定值。

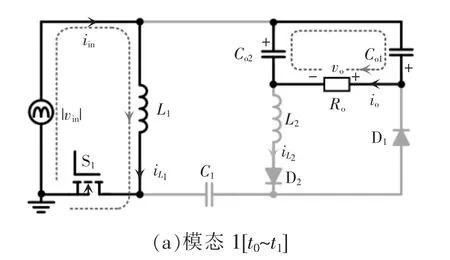
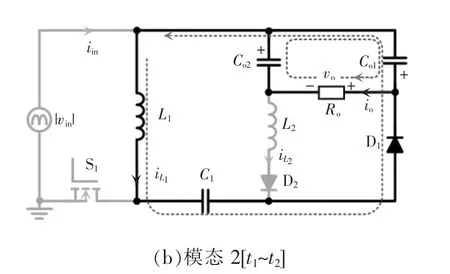
图5 在0＜ωt＜θ 和π-θ＜ωt＜π 情况下所提变换器的等效电路Fig.5 Equivalent circuits of the proposed converter in the case of 0＜ωt＜θ and π-θ＜ωt＜π

3 特性分析

对所提PFC 变换器进行理论和参数设计分析，所有的计算参数都基于56 W 的实验样机。

3.1 输入电流分析

根据第2 节的工作原理分析，在一个开关周期内，平均输入电流可以表示为

其中

根据式（9），半个工频周期内的输入功率为

式中：Po为输出功率；TL为工频周期；系数α、β 为

由式（11）得一个开关周期内开关管的导通时间为

根据式（8）和式（13），一个开关周期内开关管频率为

根据式（14）可知，在一个工频周期内，|sin（ωt）|=1时，开关管频率最小。因此，在vin为100～240 Vac、vo=80 V、io=0.7 A、L1=650 μH、L2=200 μH 的情况下，最小开关频率范围为36.5～143.0 kHz。

将式（13）代入式（9）中，可得半个工频周期内的平均输入电流为

式中，μ=L1/L2。

根据式（15），在vo=80 V、Po=56 W、vin=220 Vac的情况下，所提PFC 变换器在μ 取不同值时的归一化输入电流如图6（a）所示。由图6（a）可以看出，输入电流波形的失真随着μ 的增加而增加。在vo=80 V、Po=56 W、μ=3.25 的情况下，所提PFC 变换器在vin不同取值时的归一化的输入电流如图6（b）所示。由图6（b）可以看出，输入电流波形的失真随着vin的增加而减小。

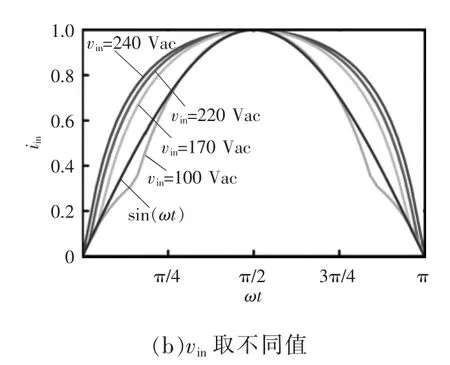
图6 μ和vin 不同取值情况下的归一化输入电流波形Fig.6 Waveforms of normalized input current with different values of μ and vin

3.2 功率因数分析

根据式（15），所提PFC 变换器的输入功率因数为

其中

根据式（16），在100～240 Vac 输入电压下，μ 的不同取值对PF 与vin关系的影响如图7 所示。当μ=1.00 时，PF 在全输入电压范围下低于0.97；当μ＞3.25 时，PF 随着输入电压vin的增加而减小，且一直保持在0.97 以上。

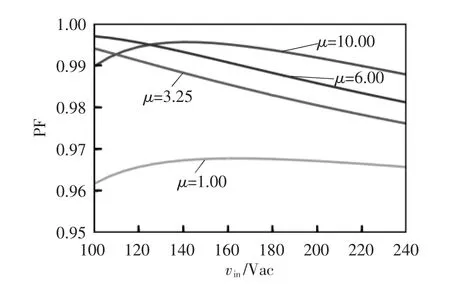
图7 PF 与vin,μ 的关系曲线Fig.7 Curves of relationship among PF and vin,μ

3.3 输入电流谐波分析

输入电流的谐波含量受μ 和vin的影响，当μ过大或者过小时，Buck 变换器和Buck-Boost 变换器的功率分配极其不均衡，并且电容C1两端的电压会非常高，导致开关管的电压应力高，因此，μ 需要在合理的范围内。本文选择μ 分别为1.00、3.25、6.00 和10.00 来分析输入电流奇次谐波含量，与IEC61000-3-2 C 类法规进行比较，在μ 取不同值的情况下输入电流奇次谐波含量与输入电压的关系如图8 所示，其中iin（n）是输入电流的n 次谐波含量，IEC（n）是IEC61000-3-2 C 类法规的n 次谐波电流限制。因为更高次的奇次谐波（大于9 次）很容易通过IEC61000-3-2 C 类法规的限制，所以在分析时可暂不考虑。

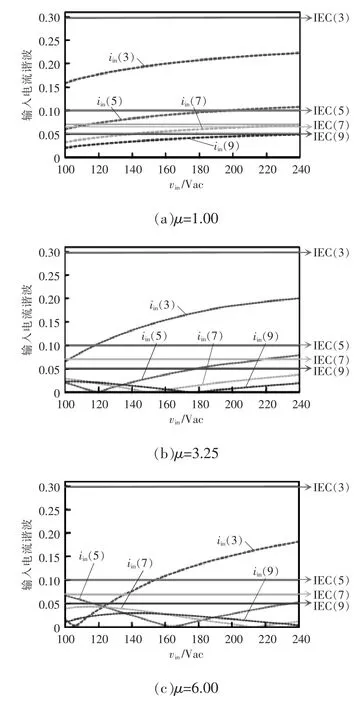
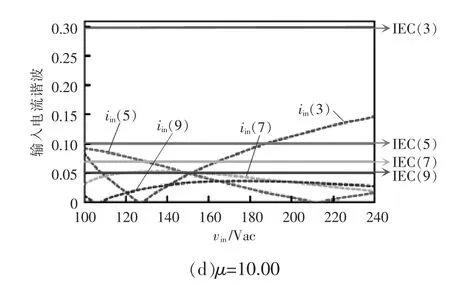
图8 输入电流各奇次谐波和vin 的关系曲线Fig.8 Curves of odd-order harmonics in input current vs vin

由图8 可知，当μ=1.00 时，5 次谐波超出了IEC61000-3-2 C 类法规的限制；当μ＞3.25 时，在全输入电压范围内输入电流谐波均可以通过IEC61000-3-2 C 类法规的限制。因此，选择合理的μ，该变换器即可在全输入电压范围下改善输入电流谐波，提高功率因数。

4 实验分析

为验证图1 所示的PFC 变换器和控制回路，搭建了一台在100～240 Vac 输入电压下的56 W 实验样机。实验参数为vin为100～240 Vac，滤波电感Lf=2.2 mH，滤波电容Cf1=100 nF，滤波电容Cf2=330 nF，L1=650 μH，L2=200 μH，C1=10 μF，Co1=Co2=680 μF，开关管S1为15NM65，额定输出电流为0.7 A，额定输出电压均为80 V。为了与传统Buck PFC 变换器进行比较，搭建了一台主电感为300 μH 的CRM Buck PFC 变换器的实验样机，其他主要电路参数与所提变换器实验参数保持一致。

图9（a）为220 Vac 输入电压时所提PFC 变换器输入电压与输入电流波形。由图9（a）可知，输入电流均可以很好地跟踪输入电压的变化，实现了功率因数校正。在输入电压峰值时，所提PFC 变换器的开关管反向电压和电感电流波形如图9（b）所示。由图9（b）可知，Buck-Boost 电感电流工作在CRM，Buck 变换器电感电流工作在DCM。输入电压峰值时开关管最大反向电压为380 V，小于开关管S1的最大反向电压，并且理论计算的开关管反向电压为376 V，实验结果符合理论分析。图9（c）为220 Vac 电压输入时输出电压和输出电流的稳态波形。由图9（c）可以看出，两个输出电容电压均在40 V 附近，完成了自动均压。

图9 所提PFC 变换器的输入电压、输入电流、开关管电压、电感电流、输出电压、输出电流波形Fig.9 Waveforms of input voltage and current,switching voltage,inductance current,output voltage and output current of the proposed PFC converter

图10（a）为所提PFC 变换器和传统Buck PFC变换器的PF 对比。由图10（a）可知，在100～240 Vac输入范围内，所提PFC 变换器功率因数均高于传统Buck PFC 变换器，且均高于0.97。图10（b）为在120 Vac 输入电压下输入电流的谐波测试结果。由图10（b）可知，所提PFC 变换器输入电流的各次谐波均远小于IEC61000-3-2 C 类规定的谐波最大值限定标准，而传统Buck PFC 变换器无法满足IEC61000-3-2 C 类规定的谐波最大值限定标准。图10（c）为所提PFC 变换器和传统Buck PFC 变换器的效率曲线，可以看出，传统Buck PFC 变换器的效率稍高于所提PFC 变换器，而所提PFC 变换器的最大效率可以达到93.5%。相比于传统Buck PFC变换器，由于加入了Buck-Boost PFC 变换器，所提变换器开关管电流应力和元器件数量均增加，导致了效率低于传统Buck PFC 变换器。

图10 所提PFC 变换器和传统Buck PFC 变换器的PF、输入电流谐波和效率对比Fig.10 Comparison of PF value,input current harmonics and efficiency between the proposed PFC converter and conventional Buck-type PFC converter

5 结语

针对传统Buck PFC 变换器输入电流谐波高和存在输出电流死区的问题，本文提出并分析了Buck 型单开关整合式功率因数校正变换器。该变换器由一个Buck PFC 变换器和一个Buck-Boost PFC 变换器通过一个开关管整合而成，简化了控制；采用恒导通时间控制，消除了Buck PFC 变换器输入电流的死区；结合Buck 和Buck-Boost 变换器的优势，该变换器在全输入电压范围下可以实现高功率因数和高效率。最后，搭建了一台56 W 的实验样机，验证了分析结果的正确性。