深水导管架平台波浪动力响应及参数敏感性分析

柴俊凯,徐辉,刘圆

(中国船级社 海洋工程技术中心,天津 300457)

随着导管架平台设计、建造、安装技术的不断发展,我国导管架平台的应用水深已达到300 m级,水深的增加势必导致平台柔性变大,结构对随机波浪的动力响应也愈发显著。因此,随机波浪动力响应研究对控制建造成本、保证结构安全具有重大意义。由于可以考虑结构的非线性,时域法计算精度高于频域法[1],尤其适用于深水导管架平台、自升式平台等对动力响应敏感的海洋结构物。SNAME[2]、ISO[3]给出了基于时域法计算自升式平台动力载荷的惯性力载荷集法。其通过分析平台在随机波浪动态和静态响应下基底剪力和倾覆力矩的最可能最大值(以下简称RMPME),分别得到基底剪力和倾覆力矩的动力放大系数,动力放大系数与静态RMPME相乘得到惯性力载荷。RMPME为最大值概率密度曲线的最可能值[4],对于基底剪力和倾覆力矩等非高斯随机过程,RMPME需要进行工程近似。SNAME给出了4种近似方法：拖曳-惯性力法[5-6]、Weibull[2]法、Gumbel法[7]和Winterstein/Jensen[8-10]法。不同学者的研究表明[11-12],Winterstein/Jensen方法从计算效率和计算精度综合考虑是最优的。同时300 m级导管架平台的固有周期接近6 s[13-14],与自升式平台极为接近,且均采用插入海床一定深度的桩或腿的方式抵抗环境载荷,因此Winterstein/Jensen方法应用于深水导管架平台在理论上是可行的,但在应用前需要对相关影响参数进行敏感性分析。为此,采用SACS有限元软件,建立300 m级导管架有限元模型,基于Winterstein/Jensen方法对其进行随机波浪动力响应分析,并开展波浪瞬态变化、模拟步长和时长、随机种子等参数对动力放大系数的敏感性分析。通过分析动力放大系数的变化规律,给出适用于深水导管架平台动力响应分析及动力放大系数计算的推荐参数,以期为今后Winterstein/Jensen法在深水导管架平台的工程实践提供参考。

1 结构有限元模型

选取南海某300 m级导管架平台,采用SACS建立有限元模型。导管架主腿、斜撑、水平撑、隔水套管、电缆护管、泵护管等圆管结构按照实际尺寸建模,其波浪载荷按照Morison方程计算;对于阳极块、登船平台等非圆管附属结构,以集中载荷模拟其水中重量,并通过修正附近圆管结构的拖曳力和惯性力系数考虑波浪载荷。该平台的主要设计参数见表1。图1为该平台SACS有限元模型。

图1 平台SACS模型

表1 主要设计参数

2 参数敏感性分析

针对深水导管架平台,通过改变Winterstein/Jensen方法的关键影响参数,以动力放大系数(以下简称DAF)作为输出进行参数敏感性分析。选取表1中的波浪参数模拟随机波浪,按照表2对随机波浪进行高斯性验证,DAF为动态和静态响应PMPME比值。

2.1 波浪瞬态变化敏感性分析

计算0°和45°典型波浪方向的基底剪力(F)和倾覆力矩(M)的DAF值。模拟时间12 800 s,最大截断值取800 s,截断后的模拟时间仍能满足Winterstein/Jensen方法的最少3 h要求,步长为SNAME推荐值0.25 s,结论如下。

1)随机波面均值μ、标准差σ随时间的变化见图2：μ比σ更快的达到稳定状态,μ在100 s左右进入稳定状态,σ在1 000 s左右进入稳定状态。因此,SNAME推荐100 s截断值不足以把随机波面的瞬态变化全部剔除。

图2 随机波面μ、σ随时间的变化

2)0°和45°方向DAF随截断值的变化见图3、4：当截断值小于400 s时,基底剪力(Fx、Fy)和倾覆力矩(Mx、My)的DAF呈较快的上升趋势;当截断值超过400 s后,基底剪力(Fx、Fy)和倾覆力矩(Mx、My)DAF的变化趋于稳定。

图3 DAF随截断值的变化(0°)

3)图3、图4中DAFmax与DAFmin相差百分比见表3。对于0°方向,最大相差5.6%,发生Fx的DAF曲线;对于45°方向,最大相差3.31%,发生My的DAF曲线。

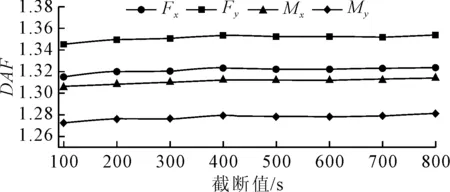
图4 DAF随截断值的变化(45°)

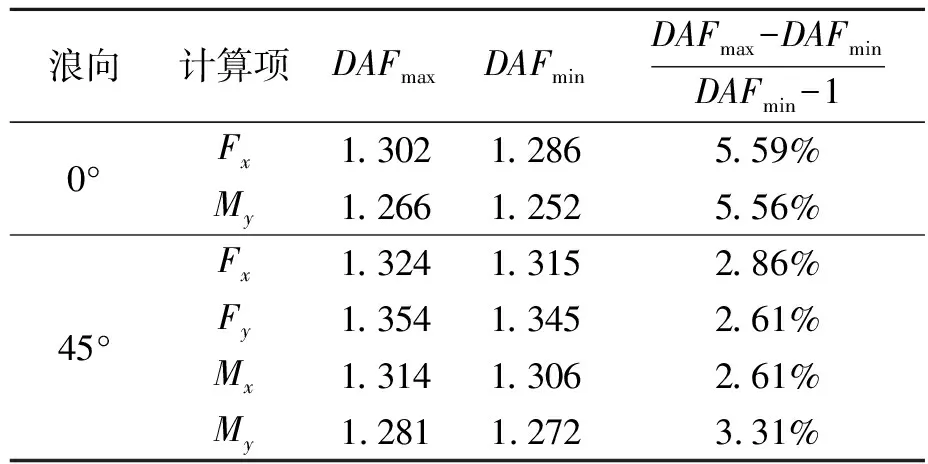
表3 DAFmax与DAFmin计算

2.2 步长和模拟时长敏感性分析

对于自升式平台,可以适当增大时间步长(1 s)和模拟时间(6 h)。但考虑到研究样本数有限、导管架平台和自升式平台结构存在差异,应用前需进行敏感性分析。采用3种步长和模拟时长组合形式,同时为避免截断值对结果产生影响,截断值取2 000 s,组合形式如下。

1)步长0.25 s,模拟时长3 h,该组合为SNAME推荐值。

2)步长0.5 s,模拟时长3 h。

3)步长1.0 s,模拟时长6 h,该组合为文献[11]推荐值。

上述组合0°、45°两个典型波浪方向的基底剪力(Fx、Fy)和倾覆力矩(Mx、My)DAF值随时间的变化见图5～10,不同步长和模拟时长DAFmax与DAFmin相差比例见表4。

图5 DAF(0°-Fx)

图6 DAF(0°-My)

图7 DAF(45°-Fx)

图8 DAF(45°-Fy)

图9 DAF(45°-Mx)

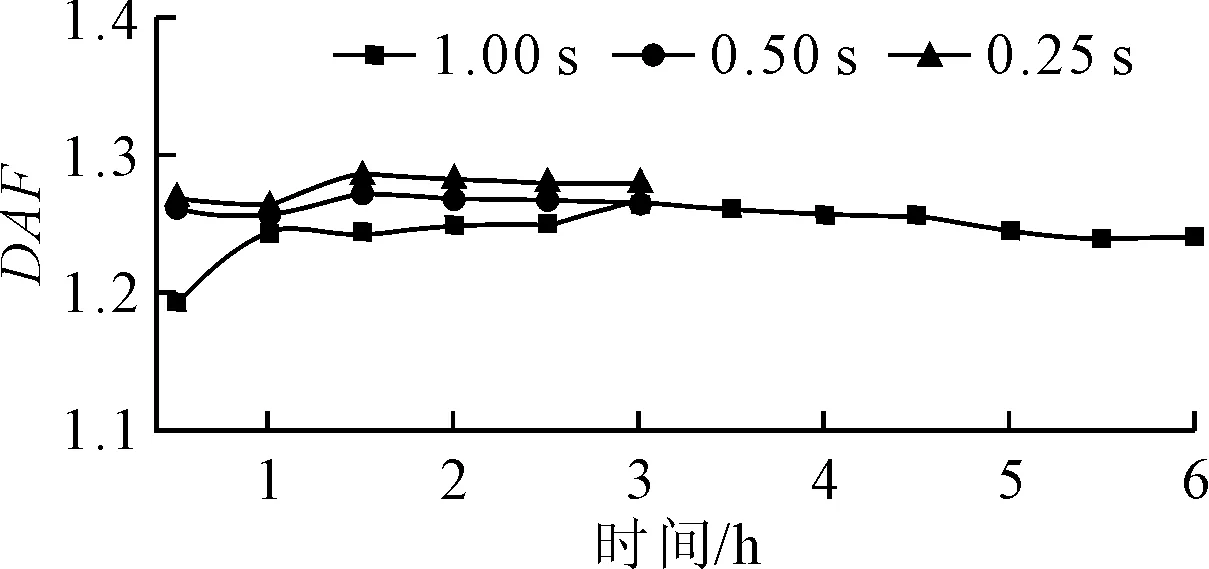
图10 DAF(45°-My)

表4 DAFmax与DAFmin计算

1)0.25 s、0.5 s步长DAF曲线。曲线变化趋势平缓,在2 h之后进入稳定状态;对于相同时间位置,0.25 s步长的DAF值略大于0.5 s步长DAF值。

2)1.0 s步长DAF曲线。在3 h之前处于极不稳定状态,在5 h之后进入稳定状态;稳定后的DAF值略低于0.25 s、0.5 s步长稳定后的DAF值。

3)由表4可知,Fx最大DAF相差18.0%,发生在180°方向;Fy最大DAF相差24.9%,发生在135°方向;Mx最大DAF相差30.7%,发生在225°方向;My最大DAF相差25.4%,发生在180°方向。

2.3 随机种子敏感性分析

Winterstein/Jensen方法仅采用1个随机波浪进行结构响应分析,在SACS中该随机波浪由波浪谱和随机种子确定,因此DAF的结果可靠性与选取的随机种子相关性极大。对于自升式平台,不同随机种子计算得到的DAF稳定性较差,因此Winterstein/Jensen方法应用前需对随机种子进行敏感性分析。筛选出3个满足高斯性要求的随机波浪,步长和模拟时间采用SNAME推荐值,进行全方向的结构响应分析,结果见表5、6。

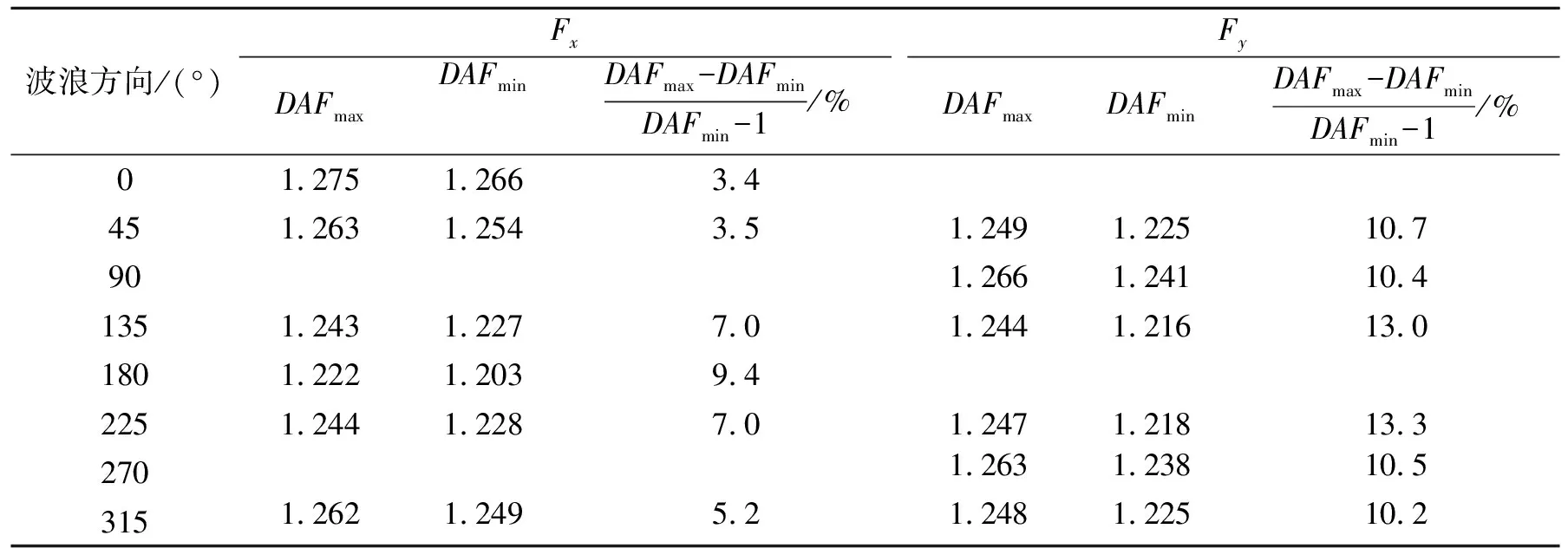
表5 DAFmax 和DAFmin 计算(Fx、Fy)

表6 DAFmax和DAFmin计算(Mx、My)

由表5、6可知：

1)Fx和Mx的DAF值离散化程度较高,在Fx、My的DAF值离散化程度较低。

2)Fx最大DAF相差9.4%,发生在180°方向;Fy最大DAF相差13.3%,发生在135°方向;Mx最大DAF相差14.6%,发生在135°方向;My最大DAF相差9.0%,发生在225°方向。

3 结论

1)DAF对波浪瞬态变化较为敏感,当截断值在400 s以内,DAF变化速率较快,相差最大百分比为5.6%,当截断值超过400 s,DAF趋于平稳,因此推荐采用400 s以上的截断值剔除海况瞬态变化对DAF的影响。

2)DAF对步长非常敏感,在未证明较大步长不会对DAF产生明显影响的情况下,应采用SANME推荐的时间步长进行随机动力响应分析,但分析时间可缩短至2 h。

3)DAF对随机种子非常敏感,采用不同种子生产海况得到的DAF离散性较大,相差最大百分比为14.6%。因此,为获得稳定的DAF值推荐取3个随机种子计算结果的平均值作为最终结果。

4)采用结论1)～3)的推荐参数,Winterstein/Jensen方法可应用于300 m级导管架平台的动力响应分析和DAF计算。但对于结构自振周期或动力响应特性不同的平台(如8腿导管架平台),建议结合平台结构特点进一步分析参数敏感性,以确保平台在波浪动力载荷下的安全性。