基于知识工程的面向船体结构总体振动的计算网格生成方法

徐思豪,陈熠画,彭亚康,吴兆年,高明星

(1.中国船舶及海洋工程设计研究院,上海 200011;2.上海交通大学 海洋工程国家重点实验室,上海 200240)

1 研究背景

1.1 结构总体振动网格的实践问题

随着船舶尺度和速度的增加,船舶产生有害振动的现象仍有发生,严重危害船舶的安全和乘员的健康。国际标准化组织(ISO)[1]、国际海事组织(IMO)[2]、各国船级社[3-5]等对船体振动噪声的要求也日益严苛。越来越多的大型船舶都需要在详细设计阶段中进行振动评估,采取必要的减振措施,以保障船员与旅客的居住舒适性、船舶设备的正常使用,以及船体结构的安全。当船舶试航时发现存在不可忽视的振动、噪声问题时,更需要通过有限元振动计算分析问题所在,分析不同方案的减振效果,计算结果往往需要进行数轮设计迭代优化。CCS的《船上振动控制指南》中对于计算模型仅要求保证模型每一个节点的3个线位移方向上都具有单元提供刚度,以防止出现低频的局部振形等原则性的要求,而对于计算网格的尺寸并未进行明确的限制[6]。

考虑到动力学计算往往会消耗较多的计算机资源,并且根据计算结果进行设计迭代优化的次数也较多。比较常规的做法是如图1所示规范中推荐的示例模型的做法,网格尺寸取桁材间距[7](一般一档强框间距等于3档肋距,因此也常被称为3S网格),其中桁材可以采用梁单元模拟[8]。这种理想化处理忽略小骨材以及开孔、连接、倒角、板缝等结构细节的影响,既能反映整体结构的刚度与质量分布保证计算结果的参考价值,又能提高FEM计算的效率。

图1 规范中的振动计算模型示例[6]

对于一些特殊船型,船东或者船级社对计算网格会有额外的限定要求,以某客滚船为例,船东着重关注每一层甲板的高阶振动,而DNV船级社根据计算效率等因素要求提供强框间距的振动模型,最终振动网格采取的方案是甲板采用纵骨间距的网格,所有垂直舱壁结构采用长条形网格,其中网格垂向以甲板间高作为间距,短边与甲板网格一致[9],见图2。

图2 根据特殊规则折减后的振动计算模型

另一方面,船舶体量的关系,使得整船计算模型的建模工作量非常大,十分耗时。在工程实践中会直接采用强度计算的模型,减少工作量,但过多的网格数量会导致计算效率较低,且网格太细会导致计算中出现过多的局部模态,对于振动隐患区域较小,仅需进行单次校核即可满足送审要求的项目较为适用,而对于有多个隐患区域,有优化需求的项目就显得非常笨重。因此也会采用折衷的方法,如图3所示,在重点区域(船尾部分)采用强度模型,而非重点区域(货舱及首部)则重新建立桁材间距网格从而降低网格数量[10]。

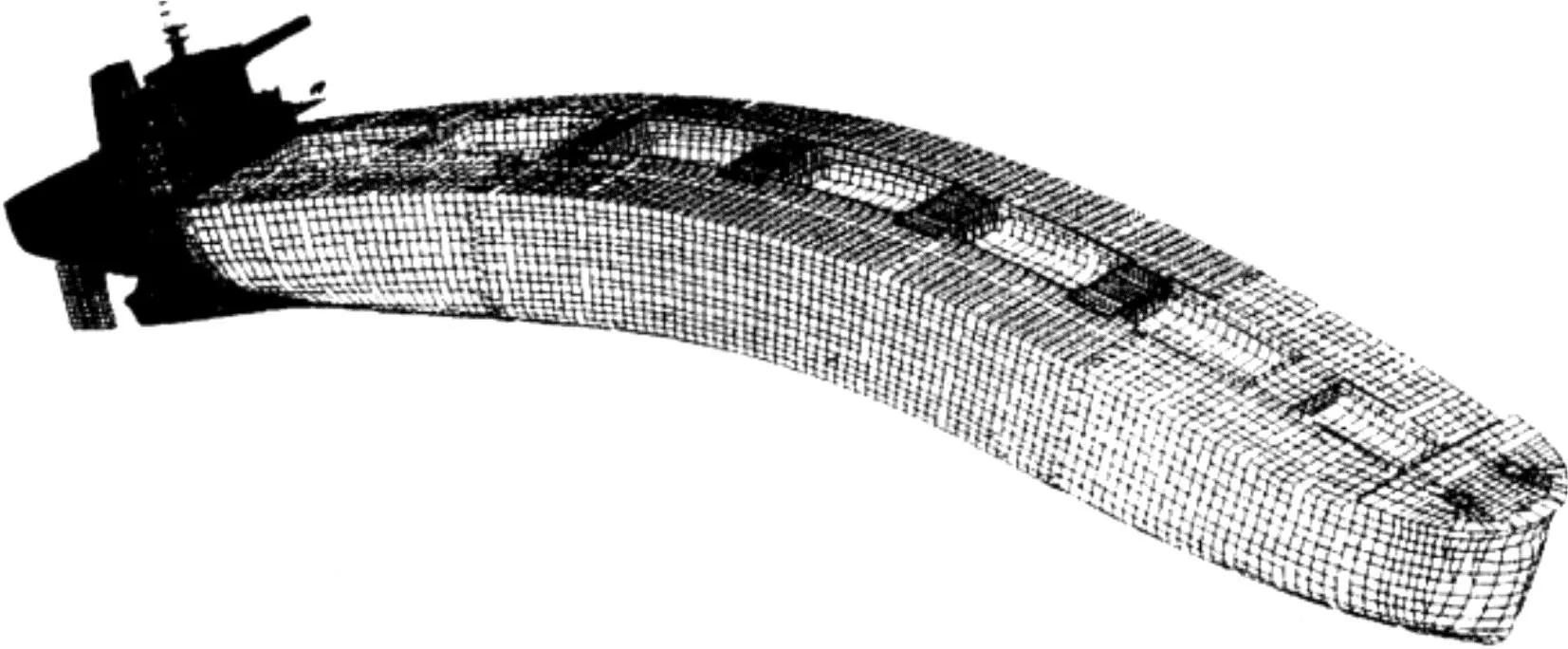
图3 混合网格示意[2]

由此可见,船体结构总体振动网格在工程实践上有以下问题。

1)由于动力学计算消耗计算机资源大,需对船体结构进行理想化,减少网格数量提高计算效率。

2)由于不同的计算目标,会存在不同的理想化原则(如图4所示为DNV具体的理想化标准)。

图4 DNV规范要求中骨材均摊算法示意图[9]

3)由于船体建模工作量巨大,重新建模往往代价过高,需要尽可能复用设计几何模型。

1.2 结构总体振动网格的技术难点

基于3DExperience三维设计软件可以构造船体结构模型用于生成常规的强度有限元模型[10]。该模型中会严格按照设计的板厚与骨材规格进行定义。而振动模型相较于强度模型是一种理想化程度更高的有限元模型,在理想化过程中可以在保持模型的刚度和质量分布不变的原则下,牺牲部分小构件以及局部几何形状。因此桁材间距模型中所有构件一般需要按照规范规定的原则进行属性均摊。

属性均摊的理想化过程主要在于以下难点。

1)骨材需要按照规范给定的原则均摊至周围的桁材上。

2)由于理想化过程调整了板缝位置以及取消了开孔,使得调整前后的板格质量会发生较大的偏差,因此需要对一个板格范围内的板厚进行校准。

3)额外考虑特殊规则,例如参照DNV的规范要求,需要进一步对不同方向上的构件进行不同原则的简化：骨材在纵向和横向位置上需要折减加密骨材,而在垂向方向上则要折减所有的普通骨材[9]。

4)属性均摊是以构件为单位进行处理的,而非直接处理把构件离散后的网格。因此直接基于强度有限元模型进行网格合并与属性修改十分困难。

5)使用常规的手工建立FEM的方法虽然能够重建网格模型,但缺点在于需要依靠人工提前计算每个单元特别是梁单元的属性再定义至模型中去。这种传统做法不仅耗时耗力,且容易由于人为的疏忽导致局部的属性定义错误或者过度简化,而且无法应对设计方案的变更。

因此,考虑基于3DE创建几何模型,基于几何进行理想化处理,再生成有限元模型。这样不仅可以保障设计信息的连续性,最重要的是保障了均摊折减是基于设计对象由程序自动计算得出的。

2 具体实现方法

2.1 骨材处理

在得到每个桁材对象下的AdditionalSection(待均摊的骨材信息)之后,即可按照骨材等效原则进行新的骨材规格求解。其中根据规范可知骨材等效原则为

(1)

式中：n为搜索阈值范围内骨材的数量,折减后的型材都采用T型材表示,其腹板高度为H(含面板厚度)、面板宽度为W、面板厚度为t1、腹板厚度为t2。αi为加权系数,不考虑骨材长度因素时皆可取1,考虑骨材长度因素时可取为第i根骨材的长度。Hi为第i根骨材的腹板高度(含面板厚度),Wi为第i根骨材的面板宽度,t1i为第i根骨材的面板厚度,t2i为第i根骨材的腹板厚度。

继续采用Action将上述算术过程转化为EKL代码从而得出新的截面规格,存放于目标桁材对象下的NewSection字段中。

需要注意的是,骨材并不是只均摊至桁材对象上,还可能会均摊至同方向的舱壁上。因此,在Action遍历模型对象时,还需要针对板材相交位置处,补充1根规格为FL1x1的虚拟桁材,就可以使得原来的知识推理逻辑能够适用于舱壁的情况。

最终,如图5所示,Action运行后使每一个桁材根据其NewSection字段自动更新其截面属性。同时也可以将所有叠加后产生的新规格输出为汇总表便于用户检查。

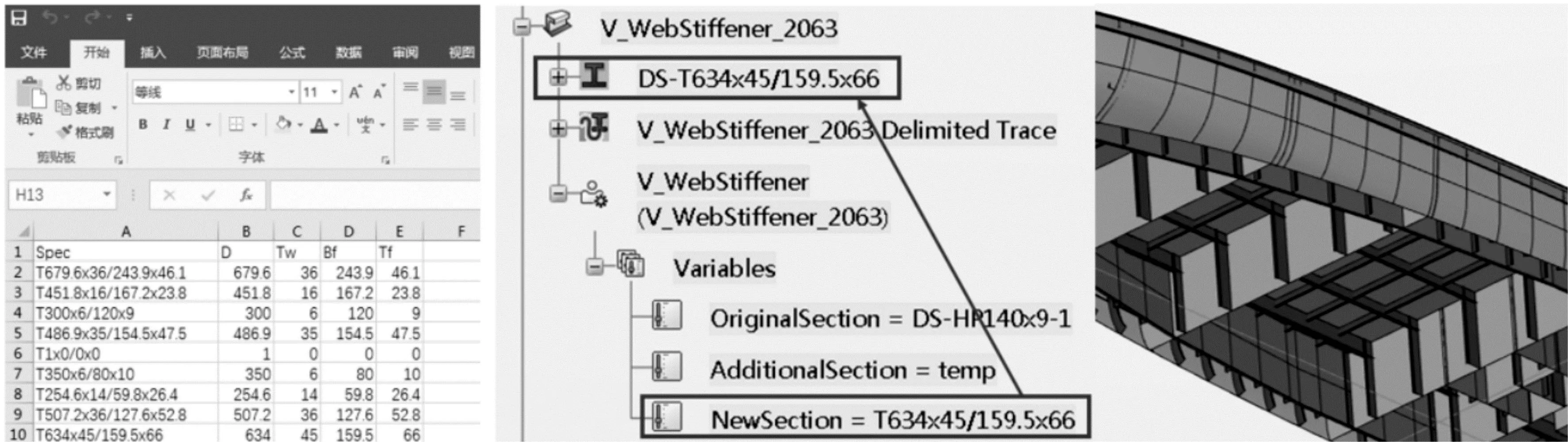
图5 骨材折减机理示意

2.2 板材处理

图6为典型的板架模型,其中板缝与桁材会错开一定距离,此外还包括开孔信息。通过板缝将整个板架分为不同面域,分别对应至了图中若干Plate对象。每个Plate对象对应其不同的厚度属性。同时开孔对象也被作为一个独立构件被存储在板架集合下。

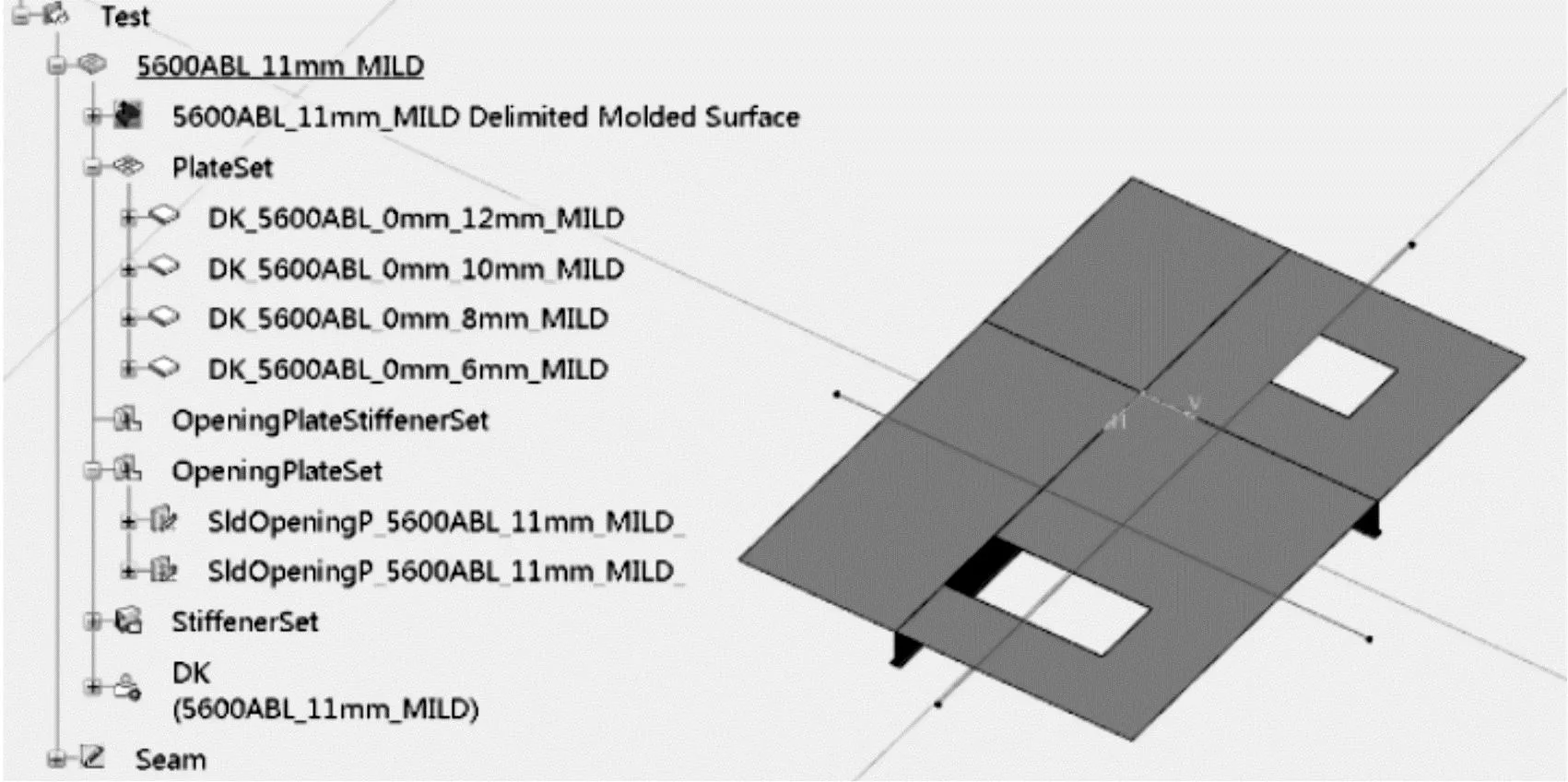
图6 典型的均摊前板材模型

根据规范板材等效原则为板厚加权平均：

(2)

式中：t为等效平均后的板厚;n为1块Panel中不同板厚的数量;ti为第i种板厚;Ai为第i种板厚的面积;AHi为第i种板厚的板中孔的面积。

要对板架进行理想化处理,需要涉及到板缝的调整,因此就会产生调整前后两个状态的板格,以及其对应的厚度属性。显然,当前的数据结构无法对上述步骤做到一一对应,因此对数据结构进行扩充,如图7所示,在模型中开设临时特征集(geometrical set)用于后续的理想化过程中不同的几何求解步骤。

图7 预处理得到的新旧板缝线

首先可以通过Action得到图7所示的原板缝线对象OriginalSeam。基于桁材迹线得到新的板缝线NewSeam,两者叠加得到BreakSeam。

如图8所示,利用知识工程与模型的交互能力分解原板架生成曲面并对其映射原始厚度。

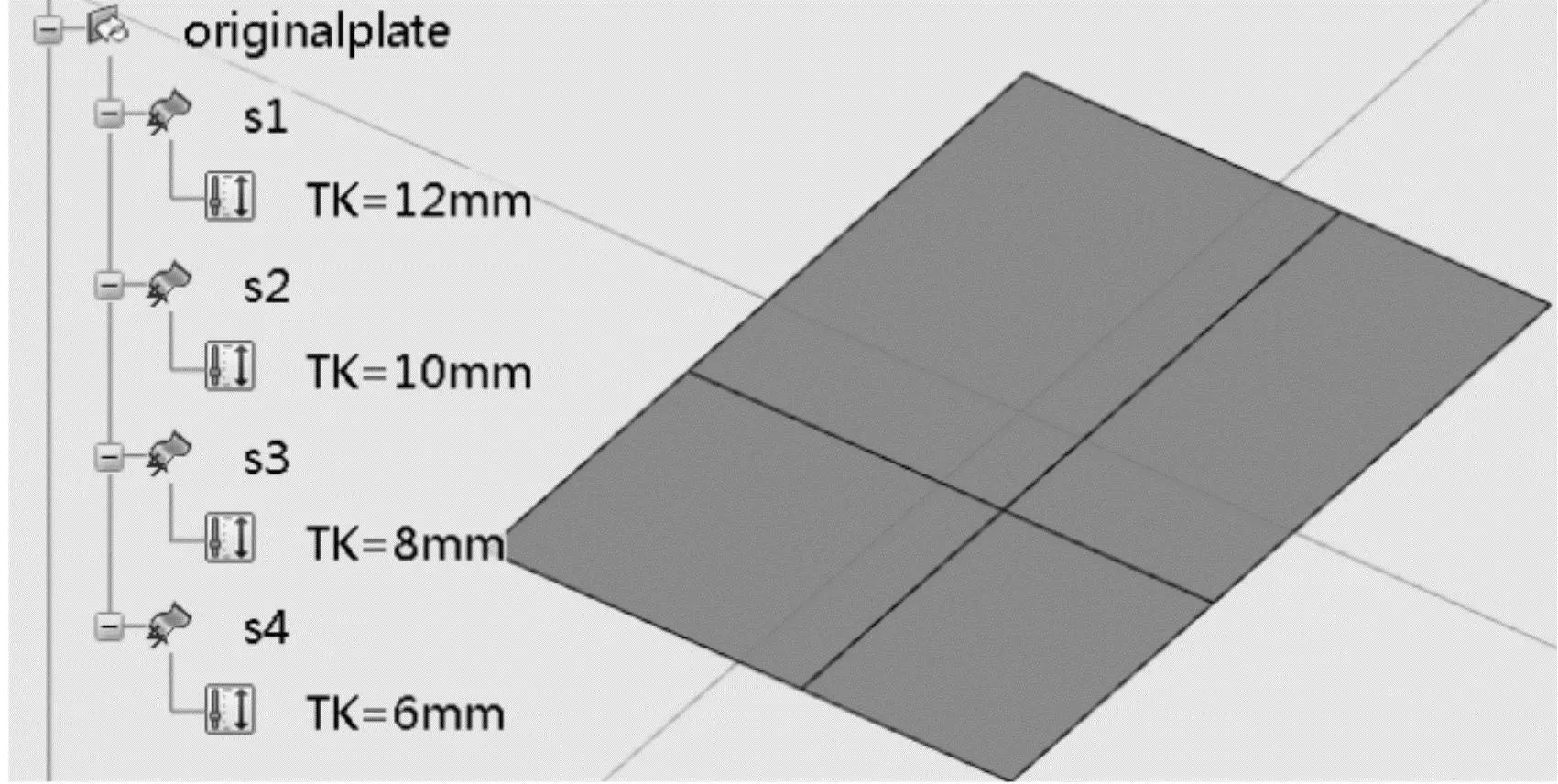
图8 分解原板架的板格并映射厚度

而后按照得到新的板缝线将原板架进行曲面的重新分解如图9所示,得到若干s1,s2,s3…等分解后的面片对象,并且在每个分解面下会添加原板厚属性。

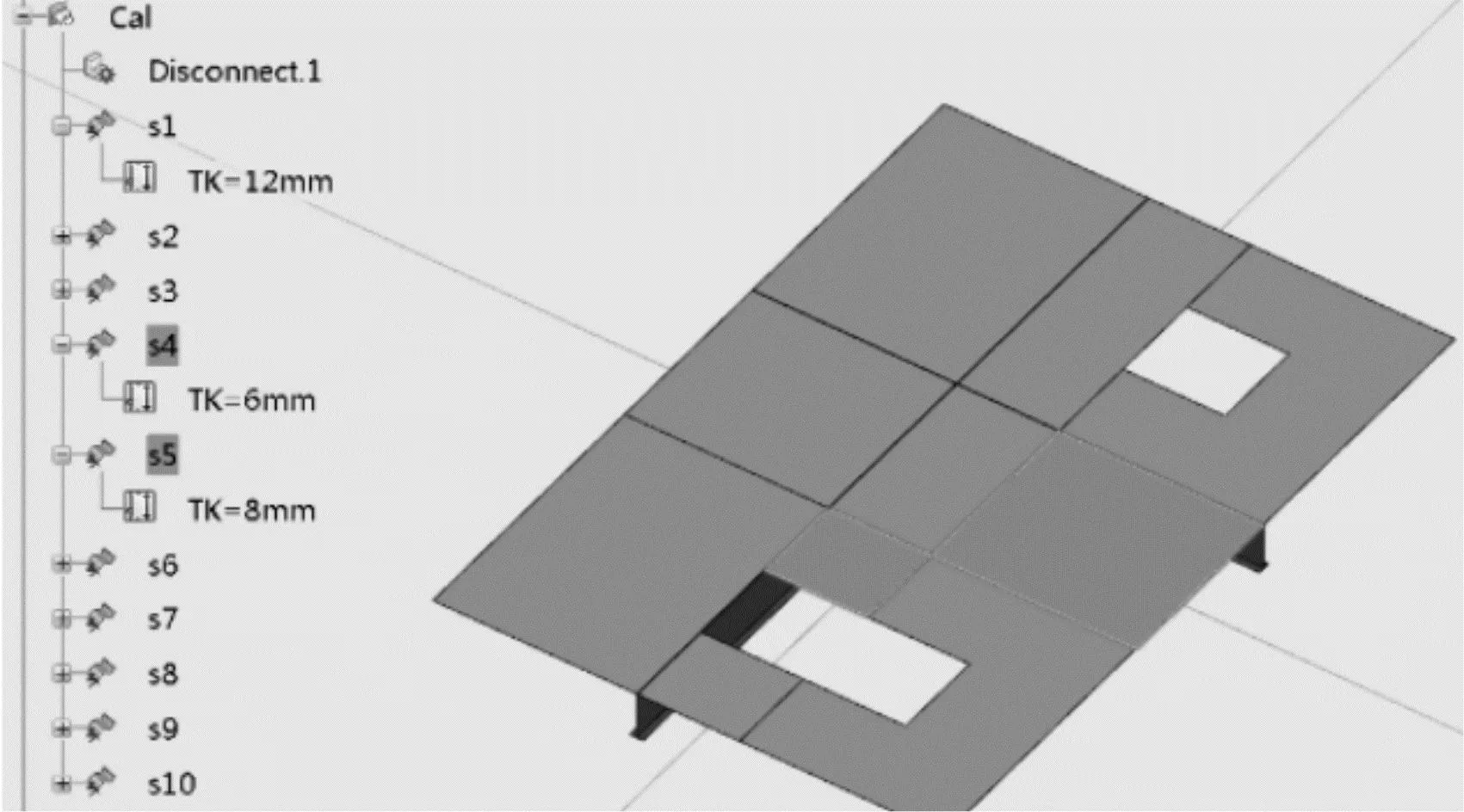
图9 重新分解厚的板厚及其厚度

而后,基于新的板缝线,得到板厚均摊后的几何。此时面域又被缩减为4个。因此根据上述s1.s2.s3…的分解结果重新按照新的区域合并子面域,并根据前后体积相同的原则计算出新的板厚。

如图10所示,可以看到根据图9中离散的7与9合并,2和8合并,3,4,5,6,10合并。最后根据新的板缝曲线,生成新的plate,并赋予对应合并后的属性。

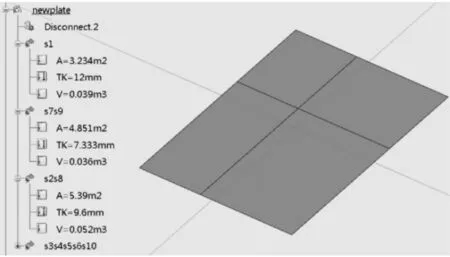
图10 根据新的板缝分隔求解新的厚度

最后如图11所示,将图10通过几何求解得到的结果再映射给同样位置的plate对象,完成板格对象的处理。

图11 将求解的新板厚重新赋给Plate对象

3 应用实例

以某客滚船为应用案例,基于船级社要求,网格尺寸要求为：船长与船宽方向上为骨材间距,需折减加密骨材;垂向上甲板间划分为1个网格。由于船型特殊性,振动网格取非常规3S网格。初始全船结构模型如图12所示,该模型基于强度网格大小,准确表达骨材、板厚、开孔等几何与属性信息。

图12 初步全船结构模型

以某一分段为例介绍具体3DE振动网格生成过程。分段初始结构模型如图13所示。

图13 初步分段结构模型

根据本文所述流程,基于图13的模型状态运行Action,获得图14所示的分段振动三维模型。最后通过FEM转模功能,转为如图15所示的有限元模型。可见,通过理想化后的几何模型生成的网格质量较好,且属性准确,见表1。

表1 强度模型与振动模型质量惯性矩比较

图14 理想化后的分段结构模型

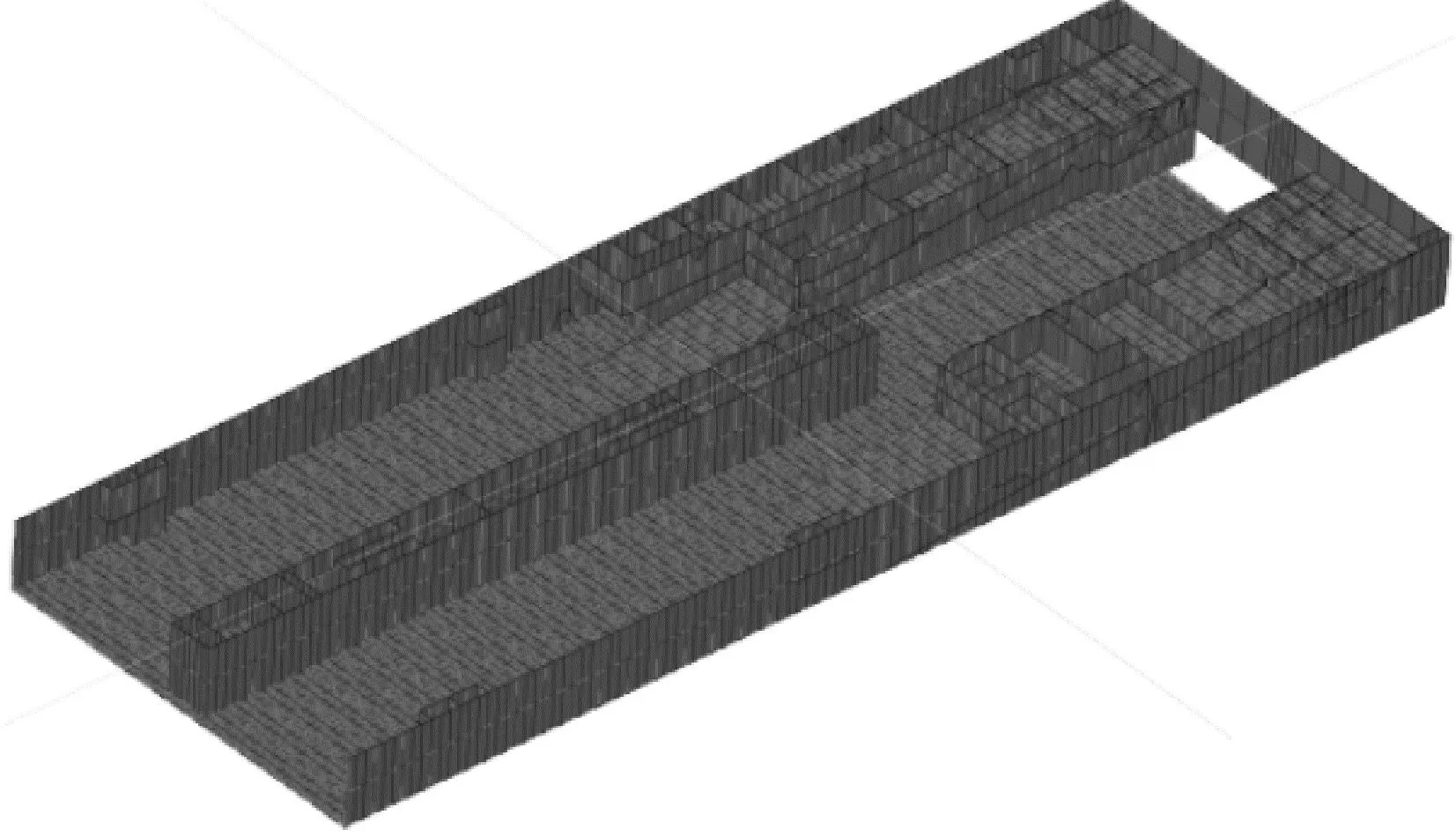
图15 振动分段有限元模型

将上述步骤对每一个分段进行操作,可得到全船三维振动模型如图16,全船强度与振动有限元模型可见图17。该船强度有限元模型网格数量为90万,节点数为45万;经过简化后的结构振动模型有限元网格数量为34万,节点数量14万,振动有限元模型在能够反映结构的动力学特点的前提上,对模型进行了大幅简化,可明显提高有限元计算效率。

图16 全船三维振动模型

图17 全船有限元模型比较

分别在强度模型和振动模型中截取FR164～FR166段,FR165模型剖面如图18所示,利用有限元软件对此段模型进行质量惯性矩统计如表1所示。强度模型与振动模型质量惯性矩的误差约为1.5%～2%,验证了振动网格生成技术的可靠性。进行全船模态分析,获得前三阶固有频率与模态如图19所示,为正式的频响分析计算提供了有效的振动模型。

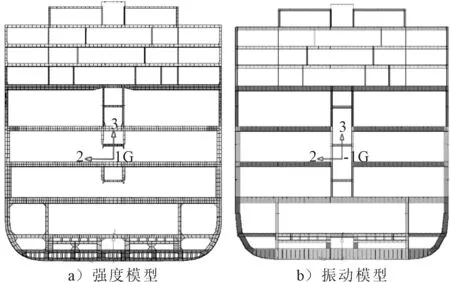
图18 强度模型与振动模型剖面比较

图19 前三阶振型与固有频率

该客滚船实际案例应用表明,基于3DE知识工程的方法进行船体振动网格建模,能够大幅减少人工计算工作量并有效提高建模效率。同时知识工程中知识与模型融合的特点可以有效支持船体模型分别输出强度网格、振动网格。为实现船舶设计模型的“一模多用”提供了有益的技术基础。

4 结论

1)以船体结构总体振动计算的仿真需求为背景,可以归纳出理想化程度高,种类多,几何复用要求等实践问题,进一步提炼了其中几何前处理过程中的属性均摊相关的技术问题,提出了一种基于知识工程的几何前处理方法来应对多样化的仿真需求。

2)基于KBE方法,将理想化原则通过知识表示与知识推理的方式与模型紧密结合在了一起,具体解决了：①由于骨材和桁材的均摊重新计算骨材规格问题;②由于板缝和开孔的调整重新计算板厚问题。相比于传统的后台化的二次开发,本方法使得理想化原则能够更为灵活的应用在建模过程中,避免增加刻板的程序化运行。

3)利用KBE与CAD模型结合度高的特性,能够基于构件对象分别实现了骨材和板材两种均摊算法,该实现方法相比传统的面向网格的手工处理方法更准确,也更能够实现自动化,和数据的可追溯。通过一条客滚船的实践案例从理想化前后的剖面模数和网格数量验证了KBE方法的有效性。

4)所提出的方法不局限于单一的仿真场景,可以推论通过KBE进一步将不同仿真需求(例如,整体、局部、强度、屈曲、疲劳)提出的不同的理想化原则与模型进行整合,从而可以满足工程设计中“一模多用”的需求,极大的增加几何模型的复用性,降低工程成本。