基于模型拖曳试验与CFD阻力计算的自升式平台主机功率估算

孟祥波,叶纪超,侯方,靖书红,罗广恩

(1.中石化胜利石油工程有限公司海洋钻井公司,山东 东营 257000;2.中石化石油工程设计有限公司,山东 东营 257000;3.江苏科技大学船舶与海洋工程学院,江苏 镇江 212000)

在设计阶段,具有自航能力的自升式平台主机功率的确定和选型至关重要。设计初期为确定平台的主机功率,通常先对平台的阻力进行测算,然后进一步推算平台的主机功率。当前对平台阻力预报的主要方法是缩尺比模型拖曳试验法,即将一定缩尺比的平台模型放到拖曳水池中测量其不同航速下的静水阻力值,然后再推算得到实际平台的阻力[1-2]。采用CFD计算方法来分析船舶阻力的研究较多,而对于平台阻力数值计算的研究相对较少[3-6]。而且,相关的研究主要是针对桁架式Spar平台在拖航中的阻力数值计算,对自升式平台的阻力数值计算较少。为此,以自航自升式平台为对象,分别采用模型试验与CFD数值计算方法分析平台静水阻力及阻力各成分的比重,并进一步对平台的主机功率进行估算。

1 自升式平台模型拖曳阻力试验

1.1 自升式平台与缩尺比模型的主尺度

在阻力试验中,模型与实际平台之间应该满足结构几何相似以及弗劳德数相等的条件,即模型与实际平台的几何尺寸应满足式(1)。

(1)

式中：Ls为实平台水线长;Lm为模型水线长;λ为实际平台与模型的比例。

依据弗劳德数相等,得式(2)：

(2)

式中：g为重力加速度。

针对目标自升式平台,在江苏科技大学船模拖曳水池开展缩尺比模型试验。根据水池的长度、拖车的速度范围等确定平台模型的缩尺比为1∶25。

模型与实际平台各个物理量之间的对应关系见表1。

表1 平台和缩尺比模型主尺度

1.2 阻力试验方案与试验结果

拖曳水池全长100 m,宽度6 m,最大水深2 m,最小水深0.3 m;轨道全长100 m;中央测桥可以向左侧池壁移动,能上、下升降,行程1.5 m,可用于完成浅水和狭窄航道试验;拖车最高车速6 m/s,最低车速0.03 m/s,稳速走车距离大于40 m,波动误差1‰。

将平台模型安装到拖车上,用压铁调整好浮态和吃水,平台设计航速为4 kn(2.05 m/s),模型速度为0.8 kn(0.41 m/s)。试验前,在对应设计航速及其附近选取0.25、0.30、0.35、0.41、0.45、0.5、0.55 m/s模型速度进行拖曳试验。在试验过程中,拖车带动模型从静止开始加速,达到预定速度后,保持匀速运动30 s左右,此时数据采集器上显示的阻力趋于稳定,记录相应的模型阻力大小。然后拖车减速至停止。返回到起点,开始下一次拖曳试验。

各拖曳速度下测得的模型阻力见表2。

在试验过程中,可以观测到在模型首部正前方有水流堆积和波面抬升的现象。不同航速的试验均有此现象,速度越高,水流堆积和波面抬升也越显著。

这种现象的主要原因是平台钝体形状造成的。这与常规的船模阻力试验相比有较大的差别。首部水流堆积会给平台带来较大的粘压阻力。自升式平台拖航静水阻力中粘压阻力占总阻力的比重较大,而船舶粘压阻力占总阻力的比重较小。因此,考虑进一步采用CFD方法对缩尺比模型和实际平台模型航行阻力进行仿真计算,分析摩擦阻力和剩余阻力在总阻力中的占比。

2 基于CFD的平台阻力数值计算

2.1 平台三维模型建立

利用三维建模软件SolidWorks,根据平台总布置图和阻力试验中的缩尺比建立1∶25缩尺比模型和1∶1实际平台模型,然后将模型分别导入STAR-CCM+软件进行网格划分及阻力计算。

2.2 计算域及网格划分

导入平台模型后,还需要考虑平台周围的流场,包括水和空气。因此围绕平台周围建立长方体几何体,然后将长方体与平台模型做布尔减运算,从而生成的体积为平台周围外流场区域,即计算域。计算域长度约7倍平台长,宽度为5倍平台长,高度为3倍平台长。流场计算域内z方向1/3区域是空气,2/3区域是水。

计算域边界条件设置为：顶部、底部和入口设置为速度入口,平台后方出口条件设置为压力出口。

生成网格的过程中,利用切割体各向异性网格单元对自由液面附近的网格进行加密处理,采用VOF法对自由液面进行捕捉[7]。整体网格数量约338万。模拟计算时选取SSTk-ω湍流模型[8],速度及压力耦合选择SIMPLE算法迭代求解,求解器参数和停止条件的设置根据库朗数公式要求,模拟时间步长设置为0.001 s,每个时间步长最大迭代次数为10次,时间设置为20 s。

另外,阻力模拟期间,在边界面和网格过度处易发生波反射现象,与波场的相互作用将导致计算结果无效,因此在VOF波区选项中阻尼条件激活,设置阻尼长度为1.95 m,从而消除波反射带来的影响。平台周围及自由液面网格细化及平台网格见图1、2,计算域边界条件见图3。

图1 平台周围及自由液面网格细化

图2 平台网格

图3 计算域边界条件

同理,将1∶1实际平台模型放入STAR-CCM+软件进行同样分析,计算出实际平台在设计航速4 kn(2.05 m/s)下的阻力。

2.3 计算结果与分析

为了验证平台模型周围流场的变化,对自由水面高度处平台周围的波形进行可视化处理,能够清晰反映出平台周围波形变化。缩尺比模型在拖曳速度0.41 m/s和实际平台模型在2.05 m/s(4 kn)时平台周围的波形见图4、5,由图4、5可见,平台在航行过程中,前方水流堆积现象明显。

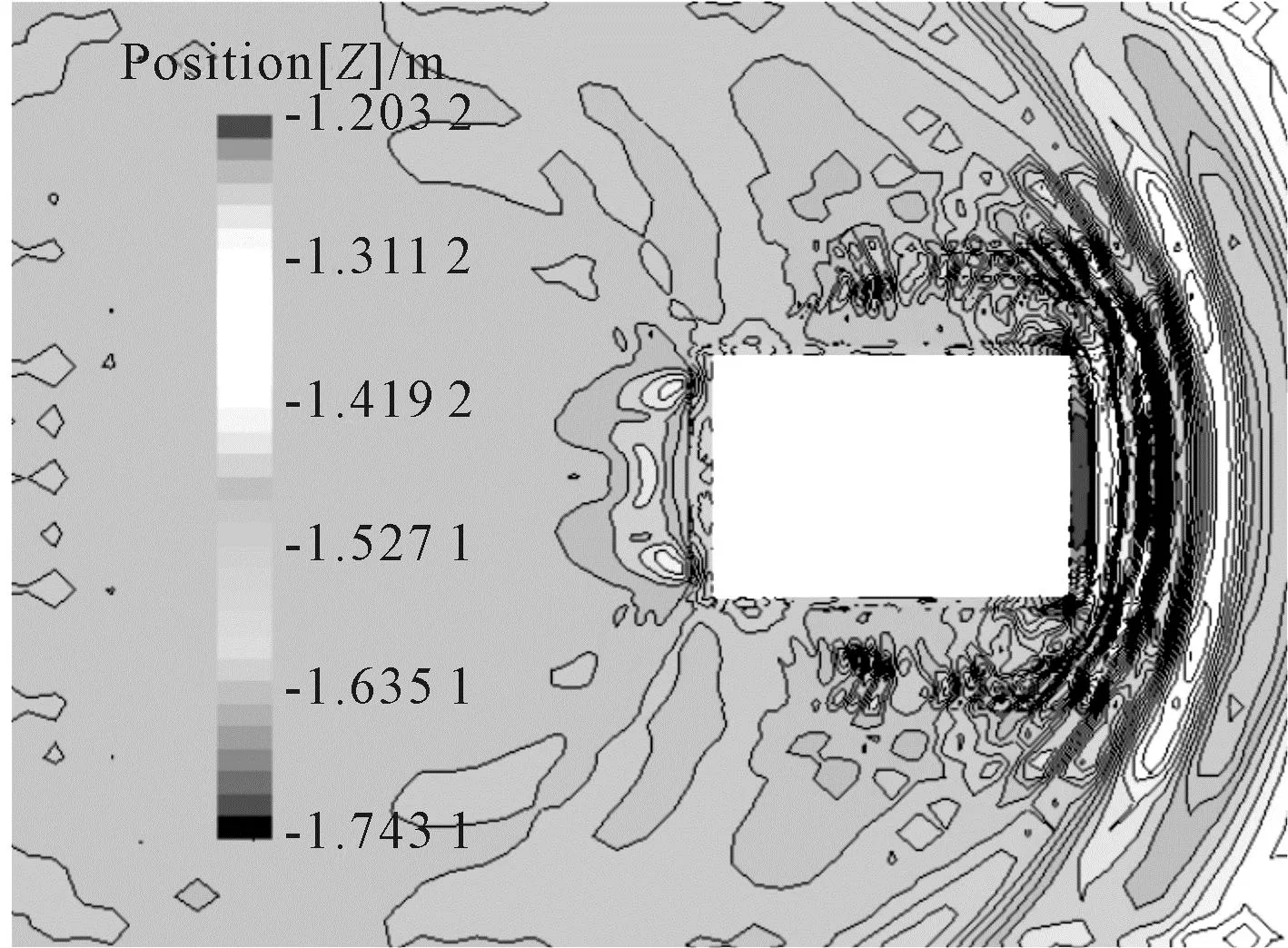
图5 实际平台模型航速4 kn时平台周围波形

设计航速下试验测得静水总阻力和1∶25缩尺比模型CFD数值模拟总阻力对比见表3。

分析表3数据可知,在设计航速0.41 m/s时,试验值与CFD模拟值误差在5%以内。验证了CFD数值模拟计算中所采用的网格划分、湍流模型、边界设置等参数设置和计算方法的可行性和准确性。

进一步分析总阻力中不同阻力成分的占比情况。在模型设计吃水0.1 m(对应于实际平台设计吃水2.5 m)状态下,通过STAR-CCM+分别计算1∶25缩尺比平台模型在设计航速0.41 m/s和1∶1实际平台模型在设计航速4 kn(2.05 m/s)下的静水阻力值。各阻力成分占总阻力比重见表4。

表4 不同计算工况下各阻力成分占总阻力的比重

1∶25缩尺比平台模型在速度0.41 m/s和1∶1实际平台模型在航速4 kn(2.05 m/s)时CFD计算总阻力随时间的变化曲线见图6、7。由图6、7可见,0～1 s内的总阻力值波动较大,在2 s以后波动明显减小,随后趋于稳定。1∶25缩尺比平台模型在速度0.41 m/s和1∶1实际平台模型在航速4 kn(2.05 m/s)时的CFD计算将总阻力按照摩擦阻力和剩余阻力结果见图8、9,由于0～1 s内还未进入稳定状态,为了曲线显示更加清晰,故从1 s开始显示。从图8、9中可以看出,摩擦阻力一直比较稳定,剩余阻力波动3 s后趋于稳定。

图6 1∶25模型0.41 m/s静水总阻力监测结果

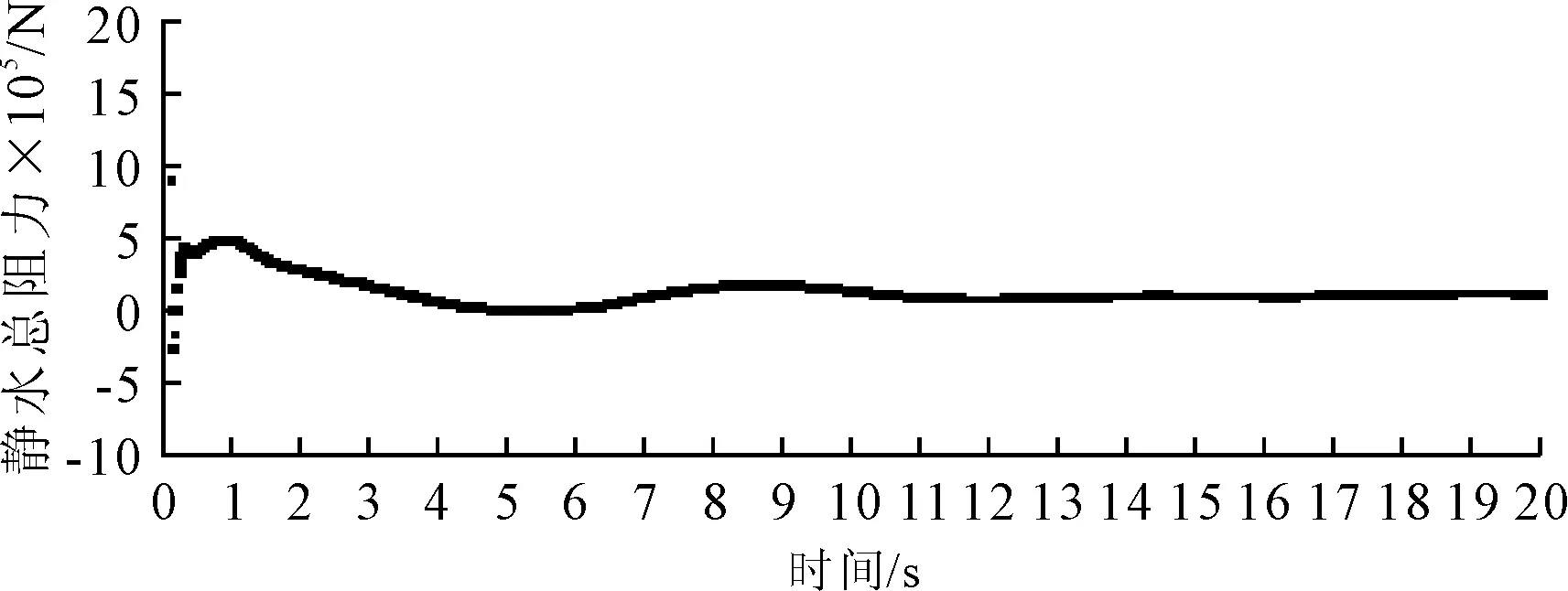
图7 1∶1模型4 kn静水总阻力监测结果

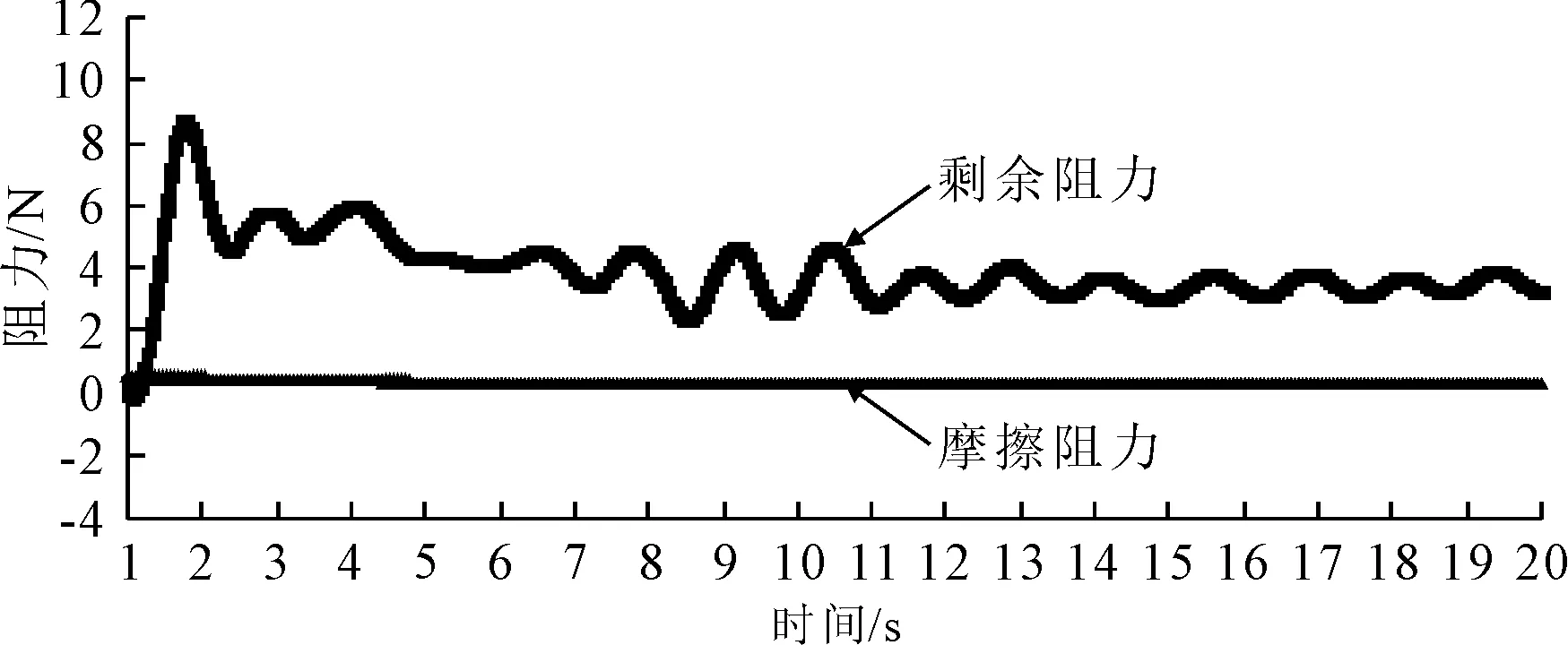
图8 1∶25航速为模型0.41 m/s时的阻力监测结果

图9 1∶1模型航速为4 kn时的阻力监测结果

由表4及图6～9可看出,剩余阻力占比90%以上,摩擦阻力占比不到10%,这与一般的船舶有所不同。常规船舶在低航速的情况下,兴波阻力小,剩余阻力也小,摩擦阻力占总阻力80%;而目标平台模型正好与其相反,平台首部钝形的形状影响,造成了水流在前方堆积和波面抬升,从而使粘压阻力为主的剩余阻力占总阻力的90%以上,而摩擦阻力仅占总阻力10%以内。因此,考虑自升式平台静水阻力成分占比的特殊性,在后续实际平台主机功率估算时应特别关注。

3 平台阻力换算与主机功率估算

3.1 阻力换算方法

平台航行所受到的总阻力可分为摩擦阻力、粘压阻力和兴波阻力。平台阻力试验只能测得模型的总阻力,所以采用弗劳德换算法(又称二因次换算法)进行模型与实际平台的阻力换算。即总阻力为摩擦阻力与剩余阻力之和。

Rt=Rr+Rf

(3)

式中：Rt为平台总阻力;Rf为平台的摩擦阻力,相当于同速度、同长度、同湿面积的平板摩擦阻力;Rr为剩余阻力。

在模型阻力试验中测得模型的总阻力Rtm,根据相似定律,实际平台与模型的弗劳德数相等时,剩余阻力系数Cr相等。

阻力系数换算公式写为式(4)和式(5)。

Ctm=Cfm+Crm

(4)

Cts=Cf+Crm+ΔCf

(5)

式中：Cf为摩擦阻力系数,平板摩擦阻力系数公式很多,这里选择1957年ITTC公式计算。

(6)

式中：Re为雷诺数。

考虑到实际平台的表面粗糙度大于模型表面,因此在实际平台总阻力系数计算过程中加上粗糙度补贴系数ΔCf=0.000 4。即

Cts=Cf+Crm+ΔCf

(7)

最终平台总阻力有效功率Pe。

Pe=RtV

(8)

3.2 平台阻力与主机功率估算

采用3.1中的二因次法对拖曳阻力试验结果进行处理,分别得到缩尺比模型阻力系数、实际平台阻力和有效功率,见表5。

表5 平台有效功率估算表

自升式平台模型拖曳阻力试验和CFD数值计算结果均表明,平台剩余阻力约占总阻力的90%以上,因此采用二因次法估算的实际平台阻力会低估其粘压阻力,相应的总阻力有效功率也将被低估。

通过表5可知采用CFD方法计算1∶1平台模型总阻力有效功率值约为二因次法推算的2.3倍。因此,采用缩尺比模型阻力试验结果来估算实际平台主机功率时应该充分考虑这一点,适当增大动力储备系数,来弥补二因次法估算实际平台阻力和有效功率的偏差,自升式平台动力储备建议选取为2.5。同时,考虑到实际平台主机发出的功率经过轴系、齿轮箱传动会有能量损失,实际效率为η1=0.8,螺旋桨也有推进效率η2=0.5等因素,实际平台总主机功率Ps按下式确定。

因此,平台总主机功率取值应为660 kW。

4 结论

1)在平台模型拖曳阻力试验过程中观测到首部有水流堆积和波面抬升现象,说明平台受到较大的粘压阻力。

2)CFD计算得到的波形图与试验中观测到的首部波面水流堆积相吻合,计算结果表明,平台在航行过程中摩擦阻力占总阻力的10%以内,剩余阻力占总阻力的90%以上。设计航速下的总阻力计算结果与试验结果误差在5%以内,验证了CFD计算平台阻力的有效性和准确性。

3)采用CFD方法对实尺度平台在设计航速下的总阻力进行数值计算,结果表明,平台总阻力有效功率为二因次法计算总阻力有效功率的2.3倍。为了弥补二因次法估算实际平台阻力有效功率的偏差,应将此倍数增为2.5。对于类似的粘压阻力占主要地位的钝体结构,采用二因次法估算其实尺度结构的静水阻力时存在较大误差,建议采用实尺寸的CFD直接计算法来计算结构总阻力。