基于水气二相流固耦合土层注气变形规律研究*
2024-02-26郭小红马健勇高文元
郭小红,马健勇,刘 彬,李 珂,高文元
(1.中国建筑技术中心,北京 101300; 2.青岛市住房和城乡建设局建管中心,山东 青岛 266071)
0 引言
城市地铁修建包含隧道和车站两部分,面临地上和地下工程环境。土质地层中隧道和基坑开挖是施工中的风险控制点,需构筑相对无水的操作环境。地下工程施工中通常采用隔水和降水2种方法,根据工艺差别,基坑施工空间大和作业调配相对容易,排水、隔渗均需被采用,而隧道环境封闭和开挖作业面小,因此只在隔水条件下施工[1]。现阶段基坑施工中常以高压旋喷桩或水泥搅拌桩形成的止水帷幕作为隔水手段,地铁隧道施工则以盾构机防水、盾尾防水、管片结构防水、注浆和冻结为主要隔水办法。虽然针对不同环境的隔水方法多样,细分场景都有相应的主流工法,但基坑和隧道透水事故还时有发生。总结事故类型可知,基坑透水形式可分为基坑侧壁透水、基坑底部突涌和管涌,隧道透水形式可分为掌子面失稳、盾尾击穿和冻结失效。分析事故原因可知,透水多发生在承压水和高透水性砂质、粉质土层中,排除因施工中人为和方案性失误,此类土层地下水发育良好、透水隔水土层交错埋藏、局部均匀径流、径流强度大,天然存在发生透水事故的风险。
工程中以“以气隔水”为原理的施工技术包括沉箱法、气压新奥法[2]、气压辅助土压平衡盾构工法等。采用压缩空气平衡土层水压的工程实践历史悠久,1841年法国工程师塔利哥(M.Triger)提出了气压沉箱法的原型;1851年英国首次将沉箱基础应用于罗切斯特铁路桥梁基础施工;1869年美国在布鲁克林大桥主塔基础施工中采用水柱法排土的沉箱法;1887年南伦敦地铁施工中采用了盾构和气压组合工法[3];1892年詹天佑修建滦河铁桥时,实现了我国气压沉箱基础的首次应用;1903年法国地铁4号线和8号线塞纳河附近车站均采用沉箱法施工;1923年日本在关中大地震后从美国引进沉箱技术用于桥梁重建;1934年茅以升修建钱塘江大桥时发明了现代沉箱法[4];1970年日本成功研发沉箱挖掘机,由此进入机械化时代;1978年德国慕尼黑地铁施工中实现了气压新奥法的首次应用[5];1981年日本再次开发沉箱法操作室远距离操作系统,由此进入无人化时代;我国于2006年自主开发远程控制无人化沉箱技术,并应用于上海轨道交通7号线12A标南浦站—耀华站中间风井工程[6-7]。基于以上技术发展史可知,气压工法广泛应用于桥梁和建筑基础、地下结构、隧道工程中,发展规模从小到大,可以辅助其他工法构筑无水环境,适用于深度40m以内的土层[8]。由于气压工法最初需要工人带压作业,与绿色安全施工理念不符,工程应用逐渐减少,但随着机械、自动化甚至智慧化的技术革新,气压工法现如今可实现无人化作业,在工程中仍有部分应用。
压缩空气的隔水机理即通过驱赶土体中连通孔隙的自由水,在压力平衡状态下,调节土体宏观渗透性。气压工法在使用时面临复杂的地下工程环境,如成层土层的非均匀性、各向异性和集中渗漏等,一般需调整覆土高度和注浆辅助[9]。在隧道领域中相同条件下,采用气压工法可加快44.1%~64.7%的施工进度,降低0.5%~6.5%的工程造价,减小约50%的地表沉降[10]。因此,继续深入开发气压工法的辅助模式,规避高气压状态下的施工环境,保持空气泄漏和隔绝渗水的平衡态,对隧道和基坑工程的绿色施工、技术扩展具有重要意义。本文介绍气压辅助施工工艺,通过理论和试验研究手段,探明力场和流场内成层土体在注气后的状态变化规律,为新工艺提供技术支撑和建议。
1 气压隔水施工工艺
气压辅助隧道施工工艺理念是将水土特征理论转化于富水土层地铁联络通道的修建工法中,以降低施工开挖范围内土体渗透率,进而隔绝地下水构筑相对无水的干作业施工环境。气压新奥法施工布置如图1所示。由图1可知,隧道开挖作业工人需通过气压闸门,施工过程完全处于高气压状态。气压新奥法强透水和弱透水上覆土层工况如图2所示,当联络通道上方覆盖强透水土层(渗透系数>0.01cm/s)时,则需在覆土范围内灌注水泥浆或膨润土[11-12]。为规避传统气压新奥法带压作业和土层适用性的缺点,设计了如图3所示新的气压隔水施工工艺。首先在联络通道开挖轮廓线外通过注浆或旋喷构筑2层隔水帷幕,其次在隔水帷幕夹层中压注空气,当地下水渗流截断后即可进行联络通道的开挖作业。

图1 气压新奥法Fig.1 Air pressure NATM

图2 上覆土层工况Fig.2 Working conditions of overlying soil layer
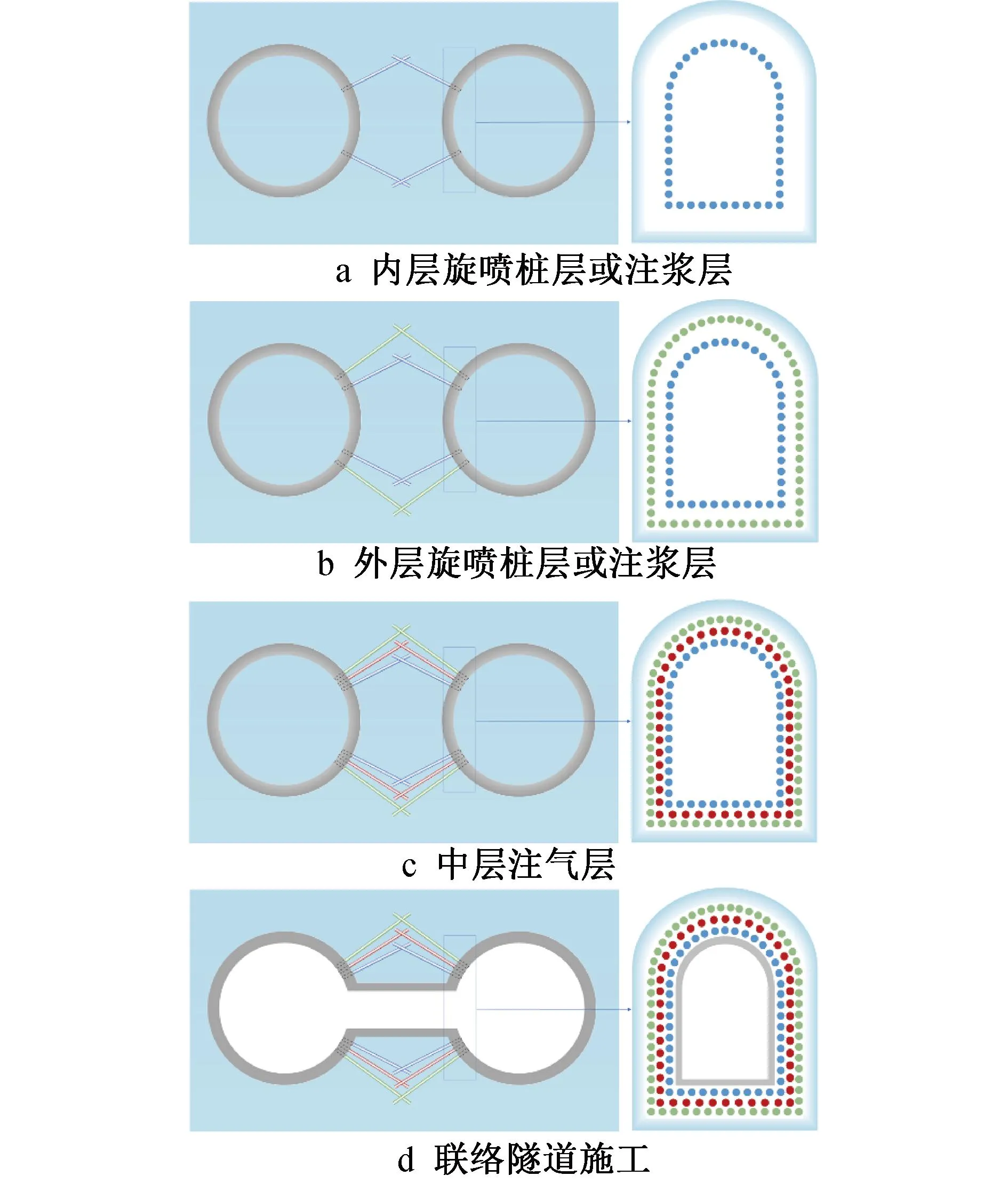
图3 区间地铁联络通道气压隔水施工工艺Fig.3 Construction technology of air-water separation in the connecting passage of interval subway
2 理论调研
压缩空气在土体中的驱替是将饱和土转变为非饱和土的过程,涉及水气二相流固耦合问题。将水、气视为相互间不混溶且不可压缩的流体[13],将土视为一种多孔介质,二相流过程发生在土颗粒连通孔隙中。土体与空气和水间存在浸润和毛细现象,一般情况下表现为对水的吸附,参考土壤学中基质吸附能力的定义,毛细压力作为其量化指标[14]。由于非饱和土体三相属性,其力学性能、渗透属性和本构关系相较于饱和土更复杂[15]。
针对非饱和土二相流理论方面的研究始于Richard,然而Richard方程描述的是宏观土体饱和渗流状态,考虑流体和土体间力学影响[16]。Biot首次将连续介质理论引入到饱和土体中的流固耦合计算中,建立了二维和三维固结模型,发展成为双向耦合固结理论[17]。Zienkiewicz在Biot理论基础上,首次提出了非饱和土体动、静态理论模型,但从耦合机制上分析该理论忽略了空气渗流对整个系统的影响,因此计算不够全面[18]。李援农等[19]通过土体入渗室内试验,证明了土体中的空气和含水率、土壤表面水层与干容重试验因素间相互影响,具有明显的减渗效应,理论模型不能忽略空气流动因素。刘晓丽等针对岩土体孔隙和裂隙均匀化的双重介质模型,基于力学平衡方程、有效应力原理、流体的连续性方程和达西定律,构筑了考虑气相影响的水气二相耦合计算模型[20]。通过对土体水气二相流和流固耦合计算理论调研可知,非饱和土体计算理论原型涉及了土力学、渗流力学、二相流动,本文研究工作面临非稳态双向耦合复杂工况。
在水气二相流固耦合过程中,二相流体在多孔介质中的物理驱替关系是其中的研究重点,即土水特征曲线。在非饱和土中含水率、渗透率和压力水头之间存在明显的函数关系,表征着土体干湿化滞回特性[21]。由于本文研究对应的是向土层内注气过程,因此土水特征曲线主要对应的是干化曲线。土水特征曲线在理论发展初期,一般在统计实测土体物理参数基础上线性回归获取,但随着理论的不断发展,一些实用的计算模型逐渐被提出[22]。现阶段通常采用的土水特征曲线模型有Brooks-Corey 模型[23]、Gardner 模型[24]和van Genuchten模型[25]等。在众多理论中 van Genuchten模型具有曲线缓和、可还原土体吸湿全过程和参数物理意义明确的优势,因此本研究中空气入渗计算选择该模型作为基础理论。van Genuchten模型应用的关键在于物理参数α,m,n的选取,现阶段针对模型取值的研究成果如下。

通过以上调研可知,van Genuchten模型参数一般获取流程为:构建理论模型、实测数据校准、误差分析和修正、模型调整后验证。因此,本文针对以上计算流程进行部分简化,采用理论结合试验进行数据反演的方式获取van Genuchten模型参数[31]。
3 水气二相流固耦合理论模型
3.1 应力场控制方程
计算过程中土体视为多孔介质连续体,以孔隙率定义其土颗粒间微观孔隙结构,其中固体力学研究部分采用Language描述,二相流体研究部分则采用Euler描述。土体稳态静力平衡方程如式(1)所示:
0=▽·σ+f
(1)
土体瞬态动量平衡方程如式(2)所示:
ρdv/dt=▽·σ+f
(2)
式中:ρdv/dt为土体运动惯性力;ρ为土体密度;σ为土体总应力(考虑土体初始应力状态,因此总应力包含初始应力σ0);f为土体外部力。
土体几何方程如式(3)所示:
ε=▽u
(3)
式中:ε为土体总应变;u为土体位移。
根据有效应力原理可知:
σ=σ′-pδ
(4)
p=Swpw+Sapa
(5)
式中:σ′为土体有效应力;p为孔隙流体压力,其中包含了孔隙水压pw和孔隙气压pa;Sw为土体中水相饱和度;Sa为土体中气相饱和度,其数值为1-Sw;δ为Kronecker符号。
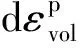
(6)
式中:K为土体体积模量。
土体本构方程为:
(7)
式中:D为土体弹塑性系数。
将式(4),(6)代入式(7)中简化后得到:
σ=Ddε-αbdpδ
(8)
αb=1-D/K
(9)
式中:αb为Biot固结系数,理论计算公式为αb=1-cs/cb,其中cs为土体颗粒骨架压缩系数,cb为土体外观体积压缩系数,本质与式(9)相同。Biot固结系数经验取值为0.5~0.8,一般采用数据拟合方法最终确定。
3.2 渗流场控制方程
根据质量守恒原理、达西定律和水气互不混溶假设可知,土体孔隙流体的连续性方程如式(10)所示:
(10)
式中:φ为土体孔隙率;κ为渗透率;κrw,κra分别为水和空气相对渗透率;μw,μa分别为水和空气动力黏度;ρw,ρa分别为水和空气密度;Qw,Qa分别为水和空气质量通量。
3.3 相场控制方程
在连续性方程中饱和度S、相对渗透率κr和土体孔隙压力▽p均未知,因此需借助van Genuchten模型建立水、空气二相流体间驱替关系,补充计算方程。在van Genuchten模型众多计算条件中,Mualem理论条件下的数值结果往往比采用Burdine理论方法的结果更准确[32],因此本文所用相对渗透率计算方程为:
(11)
式中:x为流体饱和度变化量。
在van Genuchten模型中描述土体基质全吸力范围内的土水特征函数关系为:
(12)
式中:θs为饱和含水率;θr为残余含水率;θ为含水率;S为相对含水率;h为孔隙气压力减去孔隙水压力的水头(m);α,n,m分别为van Genuchten模型3个参数,一般α为入口毛细压力水头hb的倒数,是水和空气转换的界限。其中,m,n存在m=1-1/n的约束条件,n一般控制土水特征曲线坡度。
将式(12)代入式(11)可得到:
(13)
(14)
3.4 耦合方程
水气二相流固耦合关系的建立本质上是土体应变场、渗流场和相场间动态平衡过程,耦合原理如图4所示。

图4 耦合原理Fig.4 Coupling principle
3.4.1相场-渗流场耦合方程
相场与渗流场间耦合关系是在水、气二相均质化的基础上建立的,均质化过程保证了渗流场的统一,计算如式(15)所示:
(15)
3.4.2渗流场-应变场耦合方程
渗流场与应变场间通过孔隙率φ与土体总应变ε间关系进行耦合计算。孔隙率φ随时间的增量计算需借助土体中土颗粒连续性方程求解,如式(16)所示:
(16)
式中:ρs为土颗粒密度;νs为土颗粒运动速度。
计算过程中假设土颗粒不可被压缩,即dρs/dt=0,因此土体体积变化量与孔隙体积改变量相等,土颗粒速度与土体总应变存在如下关系:
(17)
将代式(17)入式(16)可得到:
(18)
3.4.3应变场-相场耦合方程
由于土体骨架变形,从微观层面来看之间的孔隙发生改变,因此直接导致土体渗透性质也发生变化。因此,在计算过程中需根据土体变形实时修正土体渗透参数。相对渗透率和入口毛细压力水头修正分别如式(19),(20)所示[33-34]:
(19)
(20)
式中:κr0为初始相对渗透系数;φ0为初始孔隙率;hb0为初始入口毛细压力水头。
4 气压隔水可行性试验及模型参数反演
4.1 气压隔水可行性试验方法
由于粉土地层为基坑和隧道透水的事故因素,因此采用粉土作为试验样品。由试验可得,土样初始孔隙率φ0=0.436,干重度ds=2.1kN/m3,孔隙水饱和条件下的渗透系数κw=1.39×10-4cm/s。参考GB/T 50123—2019《土工试验方法标准》[35]中变水头测量饱和土渗透系数试验条文规定,试验设计一套渗透系数试验装置[36],试验原理如图5所示。该装置可向土样层中注入空气,实时监测注气压、水渗漏量和水头下降高度。

图5 试验原理Fig.5 Test principle
试验土样布置如图6所示,内径60cm的桶内由下至上依次布置透水石子、10cm厚下卧土层、3.5cm厚注气管层、30cm厚上覆土层、30cm厚水层。试验过程中共布置16根内径2mm注气管,为保证空气注入的均匀性,参考圆形截面高阶四边形网格划分方法在其节点位置布置直径0.2mm注气孔[37],注气孔布置情况如图7所示。

图6 试验粉土样本布置Fig.6 Layout of test silt sample

图7 注气管布置Fig.7 Layout of gas injection pipe
试验首先采用浸泡法使粉土样饱和,其次测量饱和土样渗透系数,最后在渗水量稳定后开始向土样中注入空气、逐级加载并同步监测试验数据。由于试验是以验证气压隔水可行性为目的,因此气压加载工况间采用连续加载的线性模式。压力统一采用大气压力相对值,加载路径如图8所示。
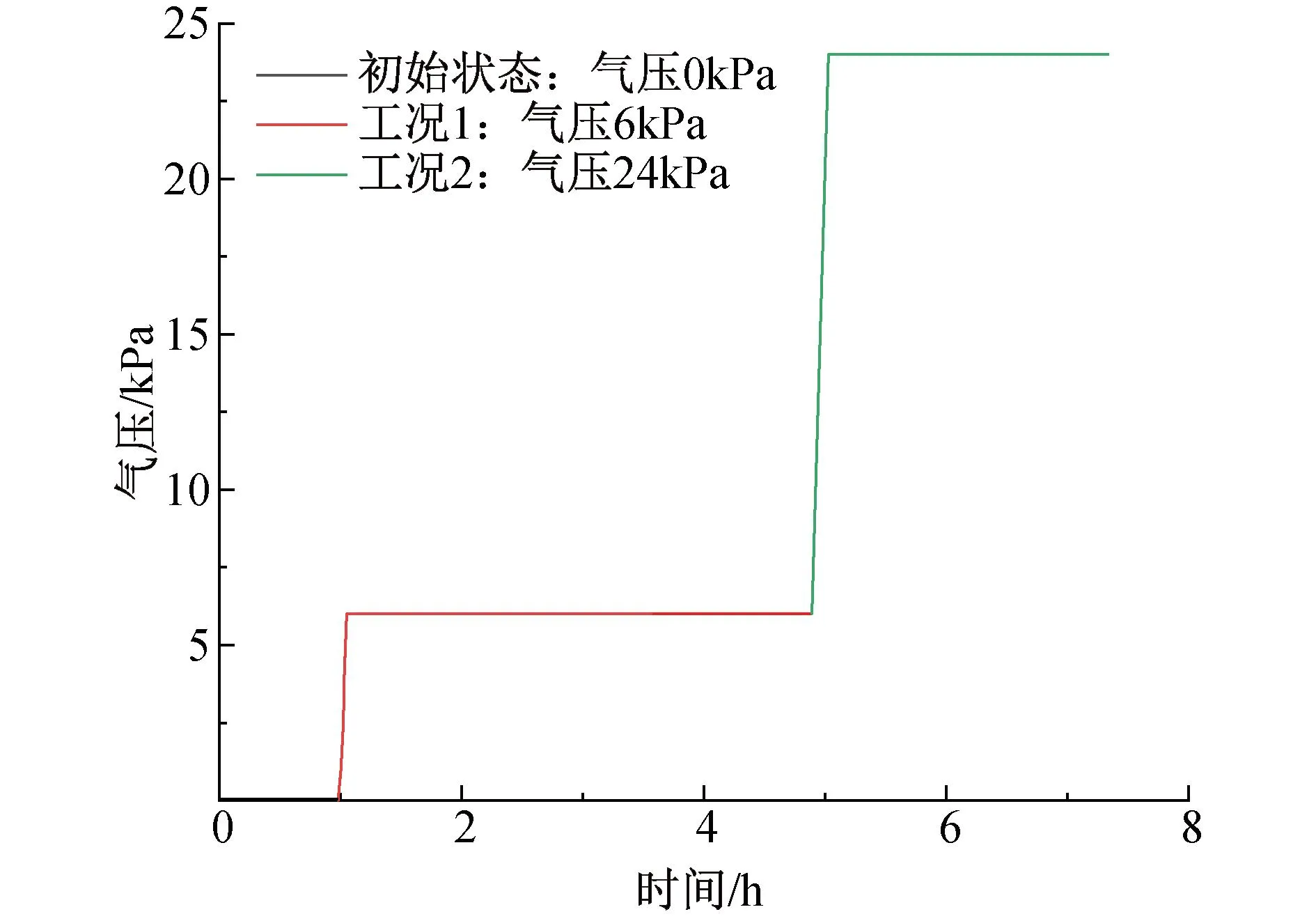
图8 注气压力加载曲线Fig.8 Loading curves of gas injection pressure
4.2 试验结果
由图9,10可知,试验土样在初始饱和条件下水层自由面的下降高度和时间呈线性关系,经计算下降速度为1.39×10-4cm/s,与渗透系数保持一致,渗水流量为0.31mL/s。注气压力6kPa时,水层自由面下降速度减小至6.87×10-5cm/s,此时渗水流量为0.13mL/s;注气压力24kPa时,水层自由面下降速度继续降低,但增量减小趋于平缓,工况时间结束时的速度为2.75×10-5cm/s,渗水流量为0.06mL/s。基于试验数据可知,本次试验注气后,气压层隔水率达80.65%。
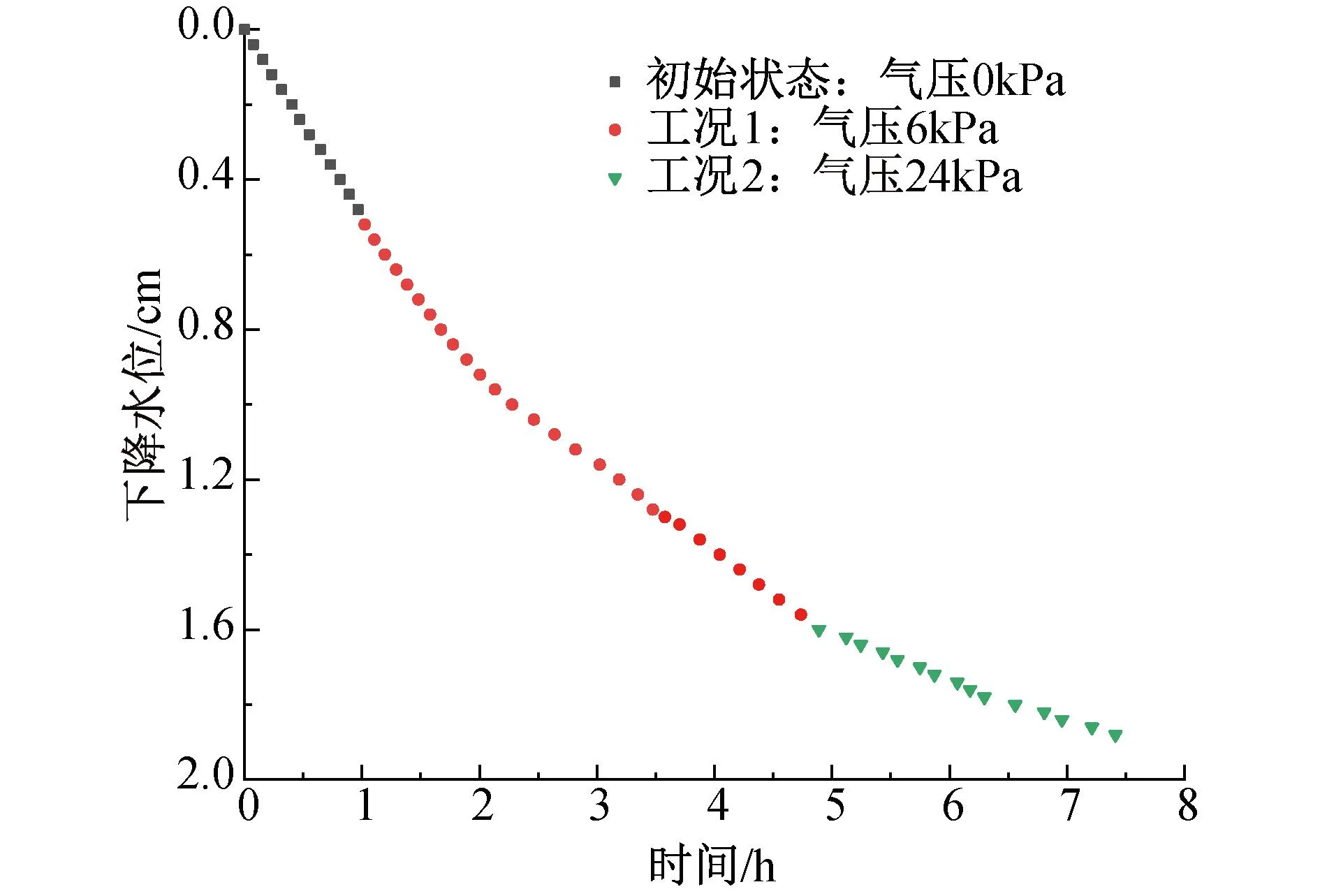
图9 水位下降曲线Fig.9 The drawdown curves
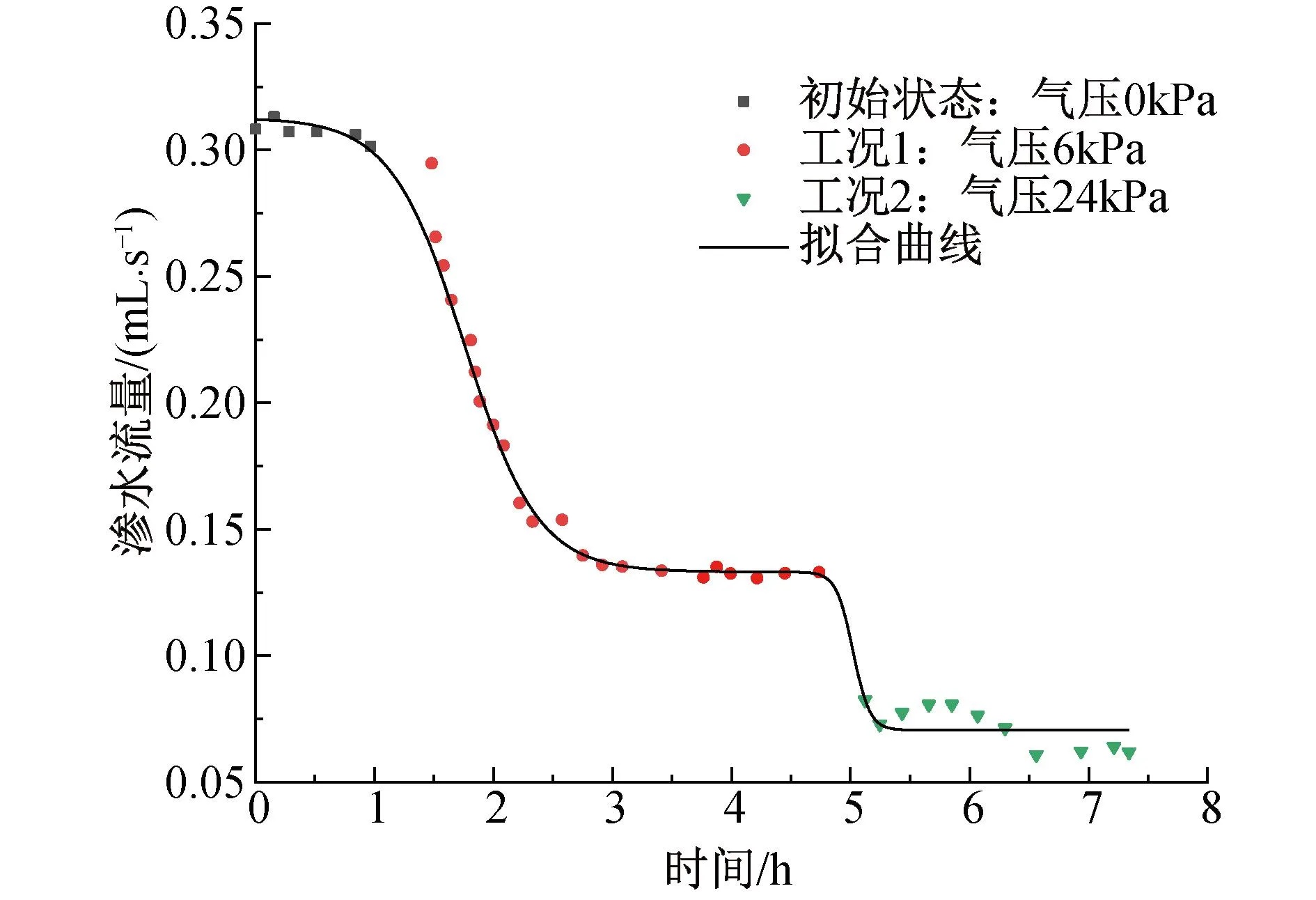
图10 渗水量曲线Fig.10 The water seepage curve
4.3 数值模型
参考气压隔水可行性试验原型,建立二维对称数值模型进行二相流固耦合理论验证和van Genuchten模型参数反演[37]。如图11所示,模型宽30cm、注气孔间距设置为14cm,模型高43.5cm。模型上边界参考图9设置为水相压力边界,下边界设置为0kPa压力条件下的开放边界,左边界设置为对称边界,右边界设置为隔水边界。注气孔参考图8中的气压加载路径设置为气相压力边界。计算模型共划分约14万个线性三角形网格单元。

图11 模型及网格划分Fig.11 Model and grid division
4.4 van Genuchten模型参数反演
根据3.3节可知,van Genuchten模型控制参数有θs,θr,α,n,m,κw,应变场未知参数有αb。由于试验中已测定θs,κw,因此未知参数为θr,α,n,αb。基于已有参数敏感性研究成果可知,对计算结果的影响程度由大到小依次为n,α,θr[38]。对于粉土n值一般为(1.31,1.85),α为(0.005,0.015),θr为(0.02,0.11)[39]。通过n,α,θr,αb间648种组合工况,以图10中的初始渗水流量0.31mL/s、气压6kPa稳定渗水流量0.13mL/s、气压24kPa稳定渗水流量0.06mL/s作为参考标准,采用式(21)计算模拟结果的标准差:
Sq=
(21)
式中:q1为0.031ml/s;q2为0.13ml/s;q3为0.06mL/s;q0.6,q4.6,q6.6分别为模拟过程中0.6,4.6,6.6h位置处渗水量。
在(n,α,θr,αb)数据集合基础上,以三次多项式为目标函数拟合Sq,应用最小二乘法计算公式中的各项系数。基于以上方法的检验值R2=0.999,拟合残差为±1.5×10-3。
计算三次多项式的极小值点为α=0.013,n=1.47,θr=0.11,αb=0.72,对应标准差为0.014 7。将求解的4个参数重新代入数值模型,渗水量计算和试验结果对比情况如图12所示。

图12 试验和计算结果对比Fig.12 Comparison of experimental and calculation results
由图12可知,模拟数据在0,1,5h处出现跳跃现象,这是因为在瞬态模拟过程中,短时间的气压增加导致土体产生超孔隙水压力,随着时间的推移,超孔隙水压力逐渐消散,恢复为静水压力。
5 土层注气变形规律分析
5.1 模拟概况
在第4节研究的基础上,建立数值模型分析空气在粉土域内的扩散规律,计算过程中调整了注气压力和埋深工况。模型的4个边界为静水压力边界,压力受到埋深的影响。注气孔布置在模型中心,直径为5cm。模型初始相场为液相,调整注气压力和埋深组合工况,当空气扩散面积和土体变形稳定后,针对数据进行规律性研究。
5.2 空气扩散面积分析
注气压力和静水压力比值(简称“注气压力倍数”)与注气压力间关系曲线如图13所示。

图13 注气压力曲线Fig.13 Gas injection pressure curves
粉土地层中空气扩散面积随着注气压力倍数的变化曲线如图14所示。由图14可知,空气扩散面积随着注气压力倍数的增加而线性增加,同时埋深增加斜率同步变化,范围从50m条件下的176.05m2/倍数线性变化至10m条件下的14.64m2/倍数。因此,提高土层中注气效果,可通过提高注气压力方式实现,但注气存在上限,上限值则需要根据5.3节中地表变形情况进行分析判断。
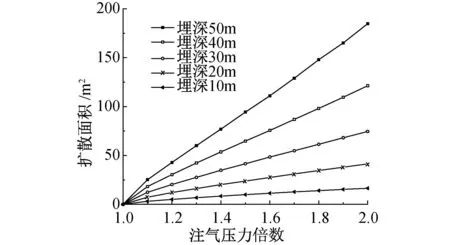
图14 空气扩散面积曲线Fig.14 Air diffusion area curves
5.3 地表隆起量分析
地表隆起量随注气压力倍数的变化曲线如图15所示。由图15可知,随着注气压力倍数的增加,地表隆起量区域平缓,埋深越大对应的地表隆起量越大。其原因是由大埋深对应的静水压力增大,相同压力倍数条件下,注气压力和空气扩散面积也处于较高水平,地表隆起量增加。由图15可判断,当注气压力>1.7倍静水压力后,注气压力对地表隆起程度影响有限。
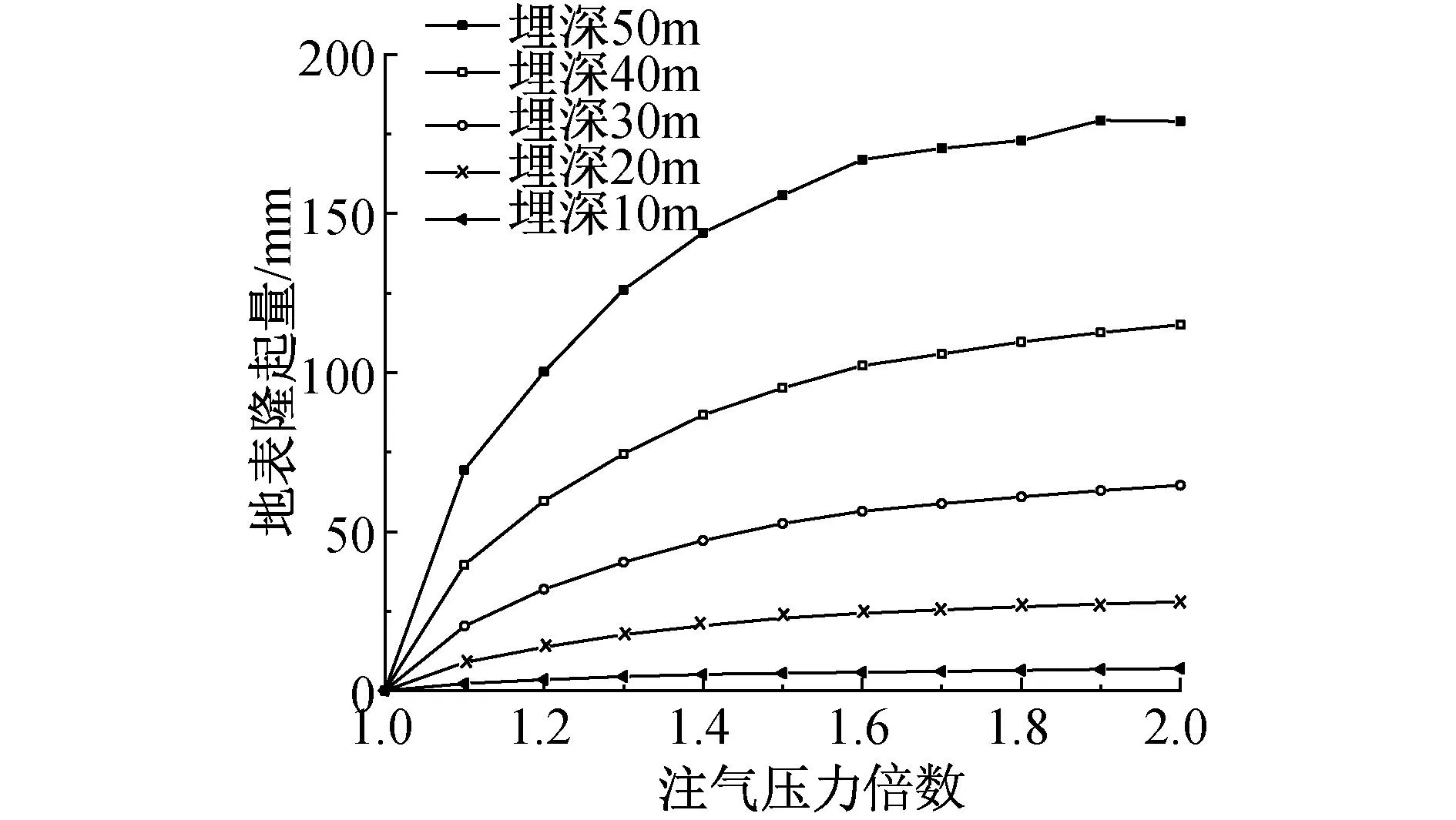
图15 地表隆起量曲线Fig.15 Surface uplift curves
由图16可知,以一般地铁联络通道断面面积16m2为例,埋深10~50m条件下,土层注气后的地表隆起量由6mm线性增加至42mm。

图16 地表隆起量与扩散面积关系曲线Fig.16 Relationship curves between surface uplift and diffusion area
6 结语
1)基于应力场、相场和渗流场所搭建的二相流固耦合理论模型可应用于气压隔水施工工艺研究,模拟还原数据真实准确。
2) 气压隔水可行性试验取得了土层内充气后渗水量明显下降的试验效果,为气压隔水施工工艺提供了初步试验支撑。
3)基于推导的二相流固耦合理论,以模拟与试验渗水量间的标准差为判据所建立的数据反演方法,真实还原了无法直接测量的van Genuchten模型参数和Biot固结系数。
4)粉土地层在注气后,空气扩散面积随着注气压力的增加而线性增加,地表隆起量则在注气压力>1.7倍静水压力后趋于平缓。
5) 在粉土地层条件下,以一般地铁联络通道断面面积16m2为例,埋深由10m增加至50m,土层注气后的地表隆起量由6mm线性增加至42mm。
