基于三点定位的特性坐标系五轴联动激光加工算法
2024-02-26高翔胡轶杰邹捷
高翔,胡轶杰,邹捷
武汉华中数控股份有限公司研究院 湖北武汉 433100
1 序言
激光切割利用高功率激光熔化或者气化工件,不同于传统金属切削需要工件装夹及对刀,存在工装设计复杂通用性差,异形曲面工件对刀空间限制等问题,现代激光切割直接将工件板材放到统一工装架上进行加工,由于是人工或机械机构直接放置加工,同一批次工件放置的角度与位置可能存在差异,每个工件放置后需要工艺人员找基准点后用CAM设计出对应的程序,加工一个工件生成一次程序[1,2],极其浪费时间。本文提出在数控系统三点定位加工方案,不同于传统机器人三点找正算法[3],工件找正包括刀尖跟刀轴的偏置,利用偏置值在系统中实现加工G代码修正偏置功能(包括刀尖轨迹及刀轴姿态的偏置),使得同一类型工件任意放置后可以使用同一个G代码加工,不用每次放置工件后在CAM中重新生成程序过程,极大地提高了加工效率,并通过了VERICUT仿真及实际加工应用验证。
2 三点定位加工基本原理
基于三点定位的特性坐标系五轴联动控制算法主要包括两个步骤[4]。
(1)工件偏移找正算法 在加工开始前,根据3个基准点在CAM中工件坐标系(WCS)与实际工件放置后的机床坐标系(MCS)下的坐标,系统解释器计算出CAM中WCS与MCS坐标系之间的关系,通过数控系统指令G68.7建立特性坐标系(TCS),坐标变换如图1所示。

图1 基于三点定位的特性坐标系五轴联动控制算法坐标变换示意
(2)刀尖点及刀轴矢量的变换算法 针对G代码中TCS下每行移动指令,将刀位点映射到WCS下,并根据当前旋转轴角度计算刀轴姿态,根据坐标系的翻转计算偏置后的刀轴姿态,最后求解得到偏置后的WCS下的旋转轴角度。
基于三点定位的特性坐标系五轴联动控制算法流程如图2所示。
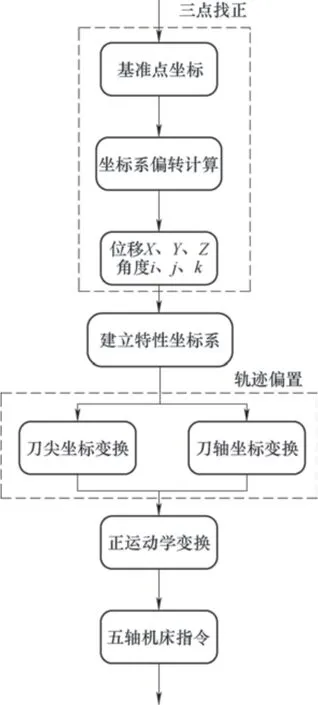
图2 基于三点定位的特性坐标系五轴联动控制算法流程示意
3 三点工件找正算法研究
本文研究的激光加工设备如图3所示,使用此类设备的激光加工工艺与金属切削相比,省去了装夹及对刀工序。加工时直接进行工件摆放,传统方式需要在工件上找3个基准点,记录3个基准点的机床系XYZ的坐标,CAM中与工件模型的3个基准点理论坐标对比,CAM自动生成根据基准点对比偏置后的G代码进行加工。此过程需要加工人员记录基准点坐标输入CAM,每重新加工一个工件都需要重新设计程序,容易出错且影响效率。

图3 激光加工设备
3.1 三点找正变换模型
三点工件找正输入为3个不共线的基准点在两个坐标系下的坐标,分别为CAM中编程坐标系与实际工件放置的机床坐标系,输出为两个坐标系之间的位移偏置XYZ及欧拉角ijk。
输入:工件上不共线三点CAM编程系坐标及实际工件机床系坐标。
输出:从机床坐标系到加工特性坐标系的转换参数(位移偏置XYZ与欧拉角ijk)。
工件找正功能总体上分为两部分:①根据输入的点的坐标值计算两个坐标系之间的平移与旋转关系[5]。②计算输出系统特性坐标系功能所需参数,即两个坐标系之间的位移偏置XYZ及欧拉角ijk。
(1)平移与旋转变换 定义CAM编程坐标系为A,机床坐标系为B,工件表面上不共线三点构建的工件坐标系为C。根据坐标系在参考坐标系中的表示可得图4和式(1)~式(3)。

图4 坐标系转换关系示意
公式中各符号的具体含义解释如下。
1)坐标系符号代表点的坐标值构成的矩阵,以A为例,A为
2)转换矩阵F可按如下方式定义(转换矩阵定义来源:《机器人学导论》)
其中,{nx,ny,nz}为坐标系在参考坐标系下X轴单位向量;{ox,oy,oz}为坐标系在参考坐标系下Y轴的单位向量;{ax,ay,az}为坐标系在参考坐标系下Z轴的单位向量;{px,py,pz}为坐标系在参考坐标系下原点的坐标,即原点的位置偏移量。
3)工件表面上不共线三点构建的工件坐标系为C,构建方法如下:以第一个点为工件系C的坐标原点,第一到第二个点构成的向量X为X轴正方向,将X与第一个点到第三个点构成的向量Z叉乘所得为Z轴正方向。
4)F的求解与含义如下。C与AB的转换矩阵F1、F2由输入的不共线的三点坐标求得后,根据公式F=F2inv(F1),求出F后,由B=FA可求得B。
由于在构建F1、F2时使用了正交的3个向量来构成,所以各转换矩阵均可逆。在4×4的F矩阵中3×3的部分即为旋转矩阵
第四列前三项即构成平移向量
任一点集在B坐标系中坐标与在A坐标系中坐标转换关系为
即任一点坐标满足
(2)欧拉角求解 平移值可如上所述直接从F中读取,旋转矩阵和欧拉角的转换关系可以由对应顺序的基础旋转矩阵的乘积计算[6,7]。以华中数控8型激光加工系统的特性坐标系G68.7功能为例,G68.7定义为以工件坐标系为基准绕Z→Y→X顺序内旋矩阵(绕旋转后的轴旋转)而得,其所得旋转矩阵与反向的外旋矩阵(绕原始固定坐标系X→Y→Z)一致,即旋转矩阵
由欧拉角旋转矩阵定义可得对应关系后反解即可得到欧拉角。此模式下旋转矩阵用欧拉角表示为
3.2 测量坐标系模型建立
在激光控制系统中,系统三点定位计算坐标系转换关系流程如图5所示。

图5 三点定位计算坐标系转换关系流程
(1)输入坐标点 输入CAM编程坐标系下三个不共线点的坐标值(Ax1,Ay1,Az1)、(Ax2,Ay2,Az2)、(Ax3,Ay3,Az3),实际测量机床坐标系下此三点对应坐标值(Bx1,By1,Bz1)、(Bx2,By2,Bz2)、(Bx3,By3,Bz3)。
(2)校验输入点坐标有效性 为保证输入点数据点的正确性从以下三个方面进行校验。
1)实际测量位置误差大于设定误差值时,报警三点定位所选三点实际测量误差大。
2)选中任意两点距离小于设定最小距离值时,报警三点定位所选三点距离过近。
3)三点构成三角形近似共线,报警三点定位所选三点近似共线。
(3)依前文所述方法构建工件表面坐标系C以CAM编程坐标系下三个不共线点的坐标值构建为例。
X方向单位向量为
Z方向单位向量为
Y方向单位向量为
同理可得实际测量机床坐标系下此三点对应坐标值构建的工件表面坐标系三个单位向量值Vbx、Vby、Vbz。
(4)计算转换矩阵F依前文所述方法由F1、F2计算转换矩阵F,此处求逆计算使用LU分解求逆以降低运算复杂度[8],LU分解的上三角矩阵和下三角矩阵为Upper、Lower,则使用置换矩阵P保证PF1可以被化简为阶梯矩阵
(5)反解平移值与欧拉角 依前文所述方法由旋转矩阵反解平移值与欧拉角。
(6)输出特性坐标系G68.7功能所需参数 即两个坐标系之间的位移偏置XYZ及欧拉角ijk。
4 轨迹偏置算法
通过三点找正输出的两个坐标系之间的位移偏置及空间角,将加工G代码中轨迹坐标进行偏置及运动学变换计算偏移后的刀尖点。
4.1 特性坐标系建立
设计带到位点与刀具姿态变换的特性坐标系功能指令。其中G68.7代表开启特性坐标系编程,后续指令刀尖与刀轴都是特性坐标系编程,X、Y、Z是特性坐标系下相对工件坐标系偏移量,i、j、k是以工件坐标系为基准绕原始工件坐标系X→Y→Z而得(此旋转同内旋,绕每次旋转后的轴旋转Z→Y→X顺序旋转),旋转后两个坐标系的方向平行[9,10]。
由前文所述的方法可知,建立特性坐标系TCS与工件坐标系WCS的变换关系为
其中T为特性坐标系相对于工件坐标系原点偏移后的坐标系的平移向量(3×1),偏移后与特性坐标系的原点重合,Rx(Ψ)、Ry(θ)、Rz(φ)(3×3矩阵)表示偏移后的坐标系与依次绕X轴旋转Ψ、绕Y轴旋转θ、绕Z轴旋转φ后的新坐标系之间的旋转矩阵。
4.2 刀位点偏移
首先在系统解释器层建立特性坐标系与工件坐标系间的变换关系,将特性坐标系下每行G代码坐标Pt:[Xt,Yt,Zt]T转换成工件坐标系下坐标Pw:[Xw,Yw,Zw]T,将工件坐标系下坐标根据RTCP算法的运动学变换计算各轴机床坐标完成插补。G代码刀位点XYZ偏移在数控系统中的处理流程如图6所示。
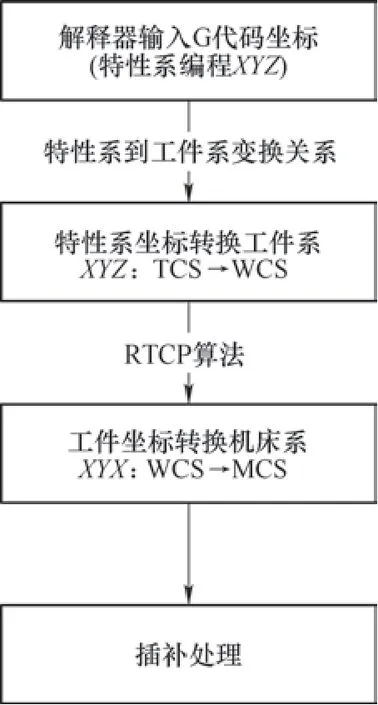
图6 刀位点偏移处理流程
特性坐标系的坐标转换到工件系变换方法为
4.3 刀轴偏置
传统倾斜面加工在建立特性坐标系后,需要刀轴摆正垂直于加工倾斜面。在建立特性坐标系时,将工件坐标系初始刀轴矢量[0,0,1]T按Rx(Ψ)、Ry(θ)、Rz(φ)旋转后,变换为在工件坐标系下刀轴矢量[i,j,k]T,再通过RTCP算法运动链关系计算出旋转轴角度。
考虑到激光三点定位后加工方式,在建立特性坐标系后刀具姿态也会在加工过程发生变换,系统需要实时对刀轴进行偏置,否则特性坐标系下编程生成的刀轴姿态会发生错误影响加工效果甚至发生干涉导致撞机。以AC双摆头机床结构类型为例阐述算法,具体G代码刀轴偏置在数控系统中的处理流程如图7所示。
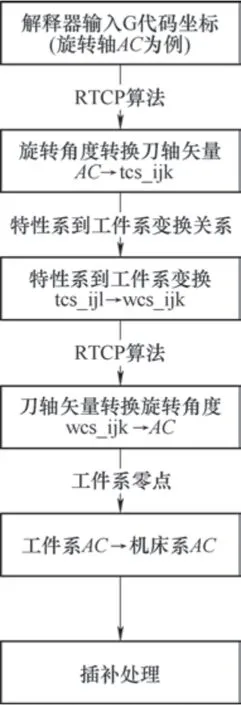
图7 刀轴偏置处理流程
5 仿真与分析
以上论述了基于三点找正算法的测量坐标系建立与求解方法,本文利用VERICUT软件对数控系统插补数据进行仿真(见图8),根据误差大小判断算法的有效性[11],最后在三维五轴机床上进行加工,根据加工效果判断算法是否有效。

图8 VERICUT仿真测试
5.1 仿真精度验证
为更好地验证算法的精度,采用NAS件五轴联动测铣进行仿真,在UG软件中,将工件放置在机床模型中任意的位置,选择工件上三个特征点,记录坐标,再将工件任意平移一定距离,旋转一定角度后,记录移动后的三个特征点在原始坐标系中的坐标。
经过测试验证,所有插补点指令精度控制在0.001mm内,满足激光切割加工精度要求,部分加工点位坐标及误差见表1、表2。
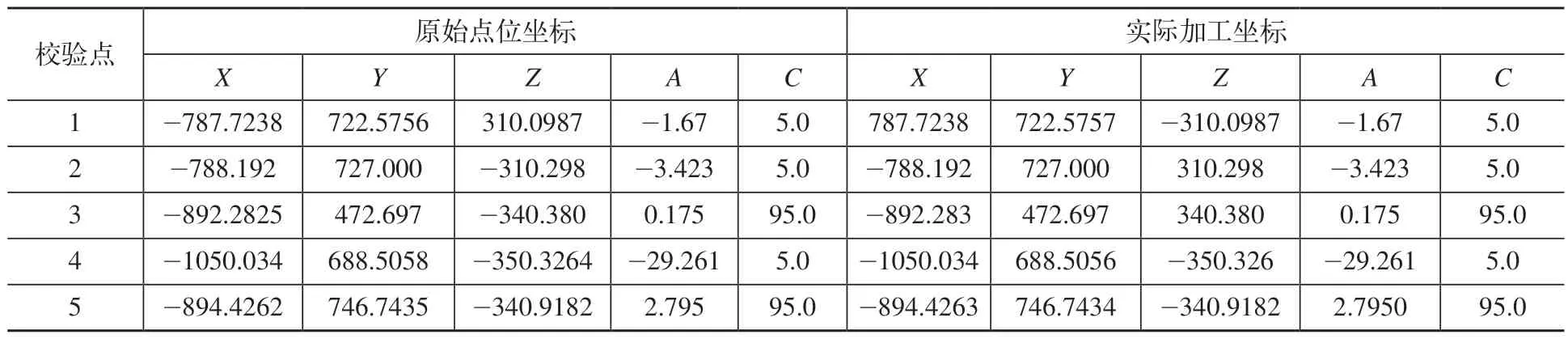
表1 模拟加工坐标 (单位:mm)

表2 模拟加工坐标误差 (单位:mm)
5.2 实际加工效果
为了进一步验证算法功能的正确性,在华工激光三维五轴激光设备上进行实际加工(见图9),并对加工出来的B柱上的特征区域精度进行测量验证。经过测试,小圆精度见表3和表4。

表3 B柱直径5mm小圆实际误差 (单位:mm)

表4 B柱直径10mm小圆实际误差(单位:mm)

图9 加工工件
经过实际加工测试,工件整体轮廓度无缺陷,小圆尺寸达标,且加工过程刀轴无干涉,满足现场应用要求。
6 结束语
本文提出了三点工件找正与轨迹偏置算法在激光加工中应用的方法,并在数控系统中实现了实时找正与加工轨迹偏置,相比原先采用CAM后置处理,大大简化了原先繁琐的加工过程,提高了效率,仿真与实际加工结果表明,加工精度符合加工要求。目前已在多个激光产品中批量试用,具有良好的应用与推广价值。
