细圆挂面接触物理参数测定与离散元仿真标定*

贾世豪，王志山，孙智聪，徐雪萌，王凤成

（1.河南工业大学机电工程学院，郑州 450001；2.河南工业大学粮油食品学院，郑州 450001）

我国作为挂面生产和消费大国，据统计2022年挂面的产量为787 万t[1]。 在如此大的需求量下，挂面自动化生产显得尤为重要。 目前在挂面生产工艺中， 研究采用容积式的计量方法对挂面进行称重计量， 但在进行容积式计量时挂面与计量仓之间的运动会造成挂面错面重叠、折断等，导致堆积密度低，影响挂面容积式计量的精度。 为了得到最佳的堆积密度，利用颗粒离散元仿真标定参数，探究了颗粒间运动规律的准确性，以及相互作用机理，进而得出挂面与计量仓， 挂面与挂面之间的相互作用及运动规律，提升挂面的容积式计量精度，降低生产成本。

离散元法是一种常见的数值模拟技术， 常用在颗粒物料分析方面。 陈林涛等[2]利用圆筒提升法和Hertz－Mindlin 无滑动接触模型开展颗粒的物理和仿真堆积试验， 通过侧壁坍塌试验对标定的参数进行了验证。 任甲辉等[3]以大长径比物料蔗段物理堆积角为响应值，采用仿真试验优化标定参数，验证了大长径比物料进行离散元标定参数的可靠性。 曹宸嘉等[4]以物理试验为响应值结合虚拟仿真实验对藜麦秸秆的粘结接触模型参数进行了校核， 验证了离散元方法标定参数的可行性。 张涛等[5]以玉米秸秆径向堆积角为响应值， 应用正交试验对玉米秸秆进行了离散元仿真，标定了玉米秸秆的最佳接触参数。侯杰等[6]研究水稻茎秆接触物理参数，以物理堆积角为响应值，利用HBP 仿真模型，通过茎秆堆积角试验、三点弯曲试验和离散元仿真标定实验，得到水稻茎秆最佳离散元参数。

研究采用执行标准为Q/LJMY 0003 S－2019 的细圆挂面为研究对象， 建立物理实验和仿真实验相结合的方法标定细圆挂面的相关参数， 为后续细圆挂面容积式称重计量仿真提供参数支持。

1 材料与方法

1.1 实验材料

选用市场销售的细圆挂面，包装规格为0.8 kg，执行标准为Q/LJMY 0003 S－2019。 随机选择20 根挂面利用数显游标卡尺和精度为0.01 的天平对挂面进行测量，得到挂面长为240 mm、直径1 mm，单根挂面的平均重量为0.34 g， 通过计算得到挂面密度为900 kg/m3。

1.2 挂面物理堆积角测定

堆积角试验与颗粒的种类、密度、形状和摩擦系数等因素有关，能直接表征颗粒物料的流动、摩擦等性质。 进行离散元参数标定，常用堆积角响应值[7]。依据文献[5，6，8]采用不锈钢抽板方法对挂面进行堆积角试验，挂面物理堆积试验如图1，重复试验10 次得到挂面堆积角的平均值为16.2°。

图1 挂面堆积角

1.3 基本接触参数测定

1.3.1 碰撞恢复系数测定

碰撞恢复系数是衡量物体碰撞后恢复到原来形状能力的参数[9]。 如果一个物体自由落体与另外一个固定物体自由碰撞，碰撞后物体自由弹起，在这个过程中，只有重力做功。 计算恢复系数e 的公式如下：

式中： e 为碰撞恢复系数；H1为挂面掉落高度；H2为挂面碰撞反弹高度。

在不锈钢板表面粘贴一层挂面，形成挂面平面，如图2（a），将挂面提升至固定高度H1，挂面自由落体运动并与挂面表面进行碰撞， 记录第1 次反弹时反弹高度H2，记录数据，重复以上操作10 次最终测得挂面与挂面表面之间的恢复系数为0.1～0.4。测量挂面－不锈钢的碰撞恢复系数，如图2（b），得到挂面－不锈钢的碰撞恢复系数为0.1～0.5。

图2 碰撞恢复系数实验

1.3.2 静摩擦系数测定

静摩擦系数反映了物体所受的最大静摩擦力与反向压力之间的比值[10]。 静摩擦系数公式为：

式中μ 为静摩擦系数；θ 为不锈钢板倾斜角度。

搭建实验平台如图3（a），对挂面－挂面静摩擦系数进行测定。将挂面径向放置在挂面表面上，逐渐改变不锈钢板的角度， 直至观察到挂面与挂面表面之间出现径向滑动， 使用万能角度尺测量此时不锈钢板的倾角，重复此实验10 次，测得挂面－挂面的静摩擦系数范围为0.15～0.35。 对挂面－不锈钢进行静摩擦系数测定，如图3（b），测得挂面－不锈钢的静摩擦系数范围为0.2～0.3。

图3 静摩擦系数测定实验

1.3.3 滚动摩擦系数测定

滚动摩擦， 物体在滚动时由于接触面的变化所受到的摩擦力。 与接触物体的材料、粗糙度、温度和湿度等因素有关，是一个有综合影响的系数。

式中：M 为滚动摩擦力偶矩；FN为正压力； f 为滚动摩擦系数；G 为挂面重力；β 为滚动摩擦临界角；r 为挂面半径。

对于滚动摩擦系数测定方法与测定静摩擦系数方法相似，把挂面沿轴向放置，测定挂面临界滚动的角度。 重复上述实验10 次测得挂面－挂面的滚动摩擦系数范围0.1～0.4。 挂面－不锈钢板的滚动摩擦系数范围为0～0.1。 滚动摩擦原理如图4，实验如图5。

图4 测定原理

图5 滚动摩擦测定实验

2 挂面堆积角离散元仿真模型创建

2.1 挂面仿真模型创建与参数设置

利用Solidworks 2020 建立挂面模型， 挂面尺寸为长240 mm、直径为1 mm，将挂面模型保存为stl格式导入EDEM 2022，如图6。设定挂面堆积仿真实验的仿真参数。 在进行仿真实验前设定挂面的颗粒工厂为BOX 模型，挂面填充为static，总质量为0.8 kg。 在simulator 中设置时间步为20%，仿真时间为1 s。 建立的仿真模型和实验如图6、图7 所示。

图6 挂面仿真模型

图7 挂面仿真堆积角实验

2.2 挂面仿真堆积角测定

挂面仿真堆积角图像如图8 所示。仿真实验中，为了更精准地测量挂面的堆积角[11]，利用MATLAB对挂面的仿真堆积截图进行二值化图像处理和边缘检测与曲线拟合，如图9、图10，最后进行线性拟合获取拟合方程。

图8 仿真堆积模型

图9 堆积模型二值化处理

图10 边缘检测与曲线拟合

3 参数标定设计与结果

3.1 仿真参数范围选取

根据查阅资料[3，4，6，12－19]，给定仿真实验中不锈钢的密度为7 850 kg/m3，泊松比设定为0.3，剪切模量设定为7.9×1010Pa， 通过计算， 挂面的密度设定为900 kg/m3。 将挂面的泊松比设定为0.3～0.4，剪切模量设定为19～109Pa。 物理实验得出了挂面－挂面，挂面－不锈钢之间的静摩擦系数、滚动摩擦系数、恢复系数的范围取值， 分别为0.1～0.4、0.15～0.35、0.1～0.4；挂面－不锈钢的恢复系数、静摩擦系数、滚动摩擦系数分别为0.1～0.5、0.2～0.3、0～0.1。

3.2 Plackett－Burman 筛选实验设计

Plackett－Burman 实验是为了筛选出对挂面仿真堆积角有显著性影响的参数。 利用minitab 设计PB 实验，以挂面物理实验堆积角为响应值，对需要筛选的8 个仿真参数的最大值和最小值作为高低两水平，用符号X1～X8分别代表这8 个参数。以中间值为中心点，共进行13 组实验。PB 仿真实验参数表如表1 所示。

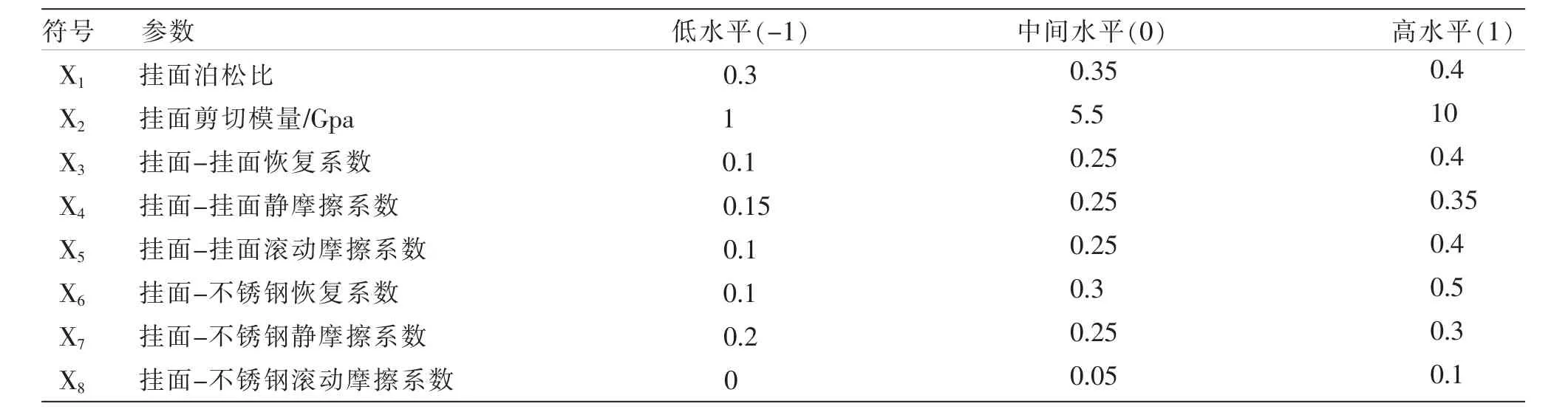
表1 Plackett-Burman 仿真实验参数表

根据表2 PB 仿真实验的结果， 利用minitab 软件对PB 试验仿真堆积角进行方差分析， 如表3 所示。 由表3 知挂面－挂面恢复系数（X3）和挂面－不锈钢恢复系数（X6） 对挂面的仿真堆积角影响极显著（P＜0.01）；挂面－不锈钢滚动摩擦系数（X8）影响显著（P＜0.05）；其它参数对挂面仿真堆积角影响不显著。

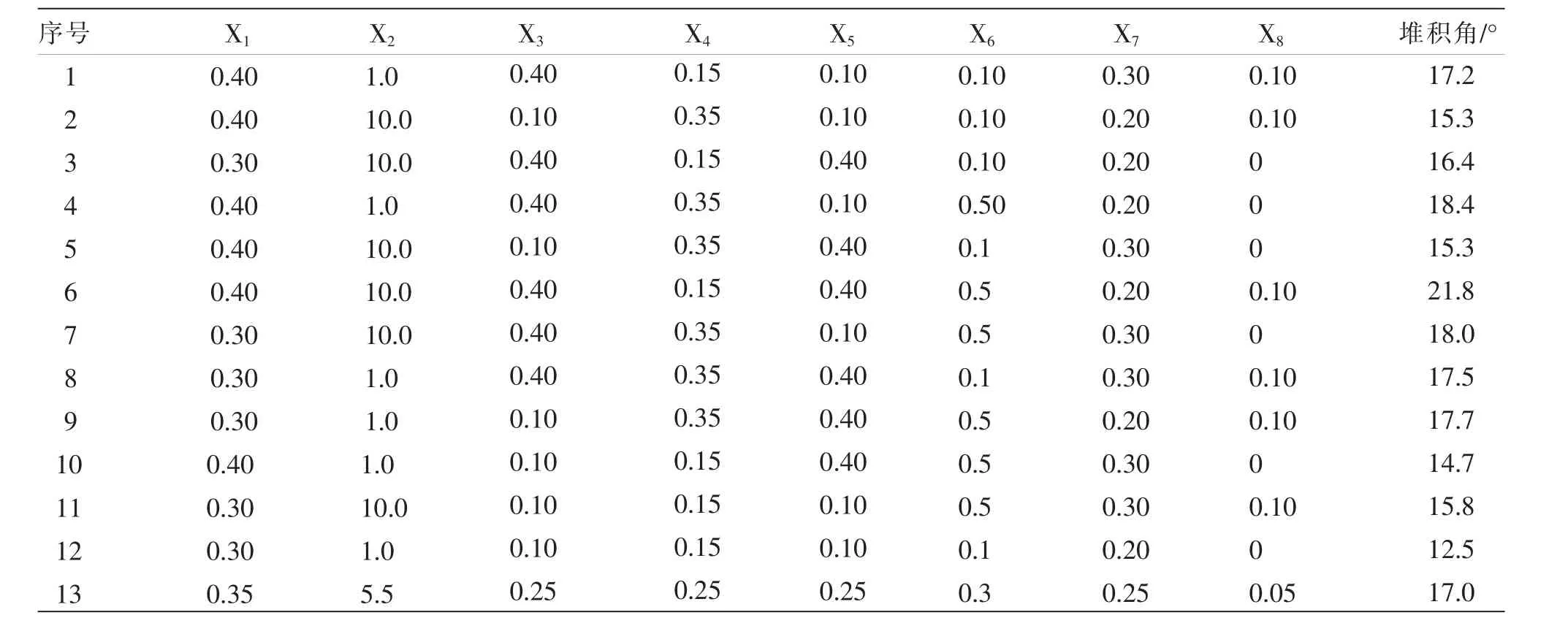
表2 Plackett-Burman 实验结果

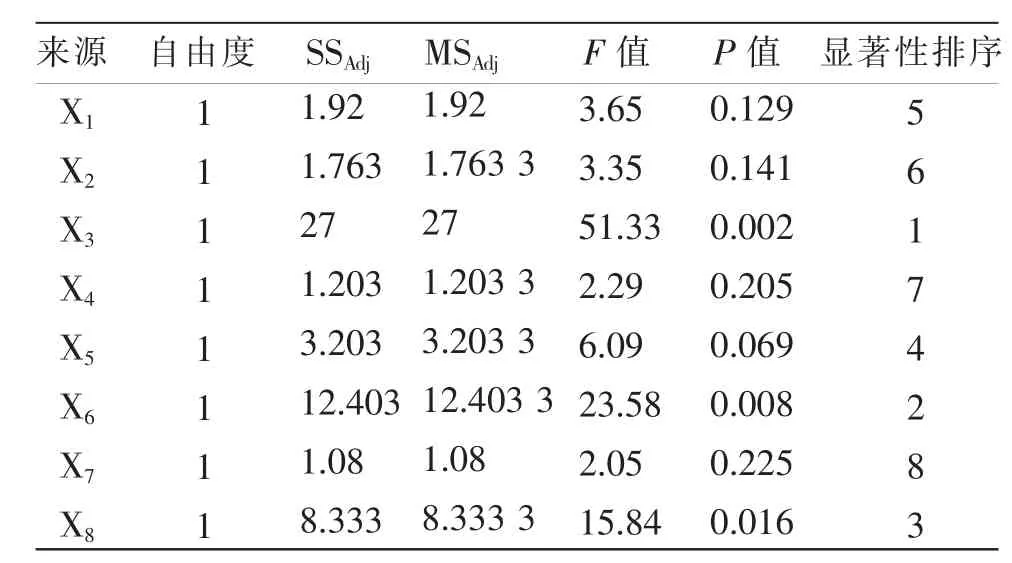
表3 Plackett-Burman 实验参数显著性分析

3.3 最陡爬坡实验

通过对PB 实验参数方差分析， 对筛选出3 组显著性参数挂面－不锈钢恢复系数、挂面－挂面恢复系数、 挂面－不锈钢钢板滚动摩擦系数进行最陡爬坡实验，其它参数取中间值。 对3 组显著因素选取6梯度，对于其它不显著参数取中间水平，进行6 组实验，实验结果如下，通过计算，第4 组相对误差最小，以此组为中心点，上下取低、高两水平进行响应面设计。 最陡爬坡实验方案设计与结果如表4。

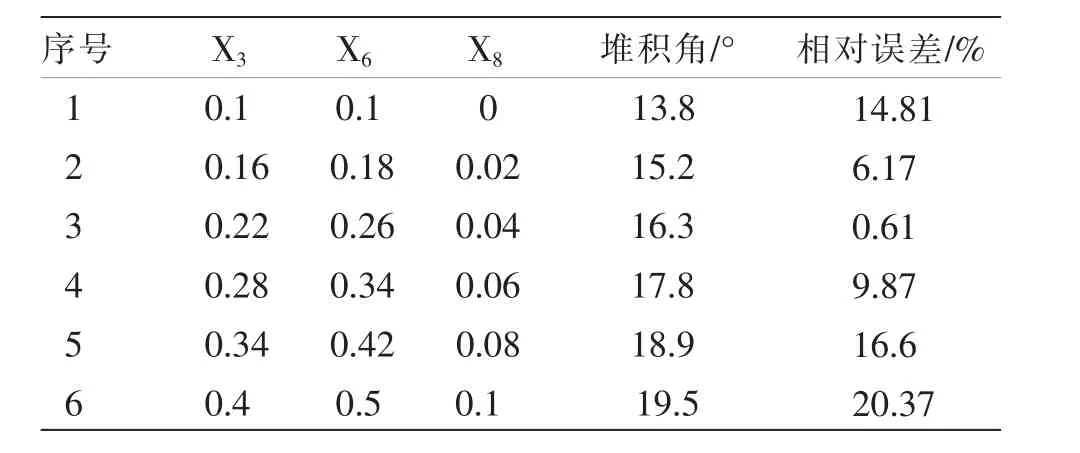
表4 最陡爬坡实验方案设计与结果

式中:Y 为相对误差；α1为最陡爬坡实验仿真角；α 为物理实验堆积角。

3.4 Box－Behnken（BB） 实验及回归模型

根据最陡爬坡实验结果， 将其中2，3，4 组实验作为依据， 对显著性参数进行Box－Behnken 实验，2、3、4 组的参数分别为低水平（－1），中间水平（0）和高水平（1），Box－Behnken 实验参数列表如表5。

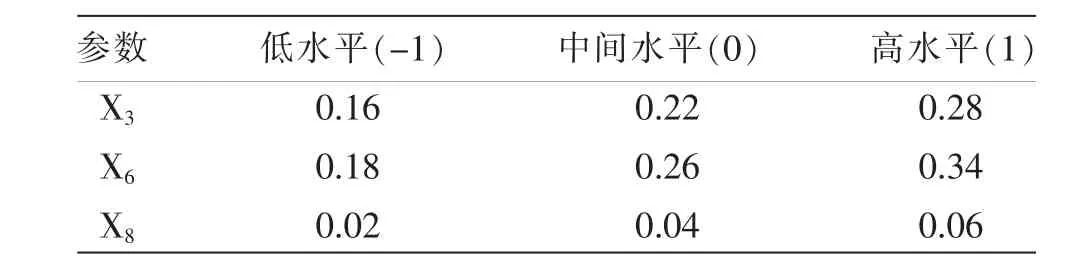
表5 Box-Behnken 实验参数列表

为了找寻最优参数， 利用minitab 软件进行Box－Behnken 实验方案设计， 方案设计及结果如表6 所示。

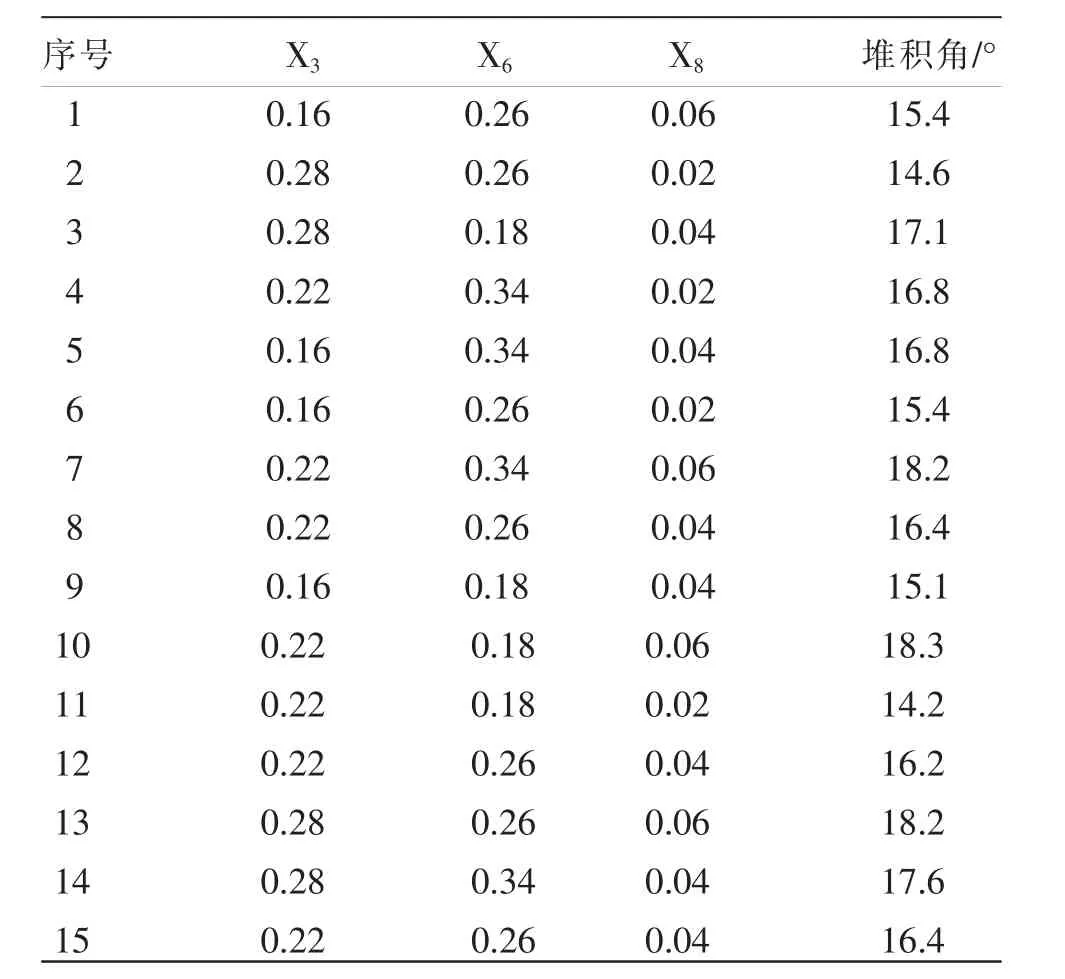
表6 Box-Behnken 实验方案设计与结果

利用minitab 软件对BB 实验结果进行响应曲面分析，得到回归方程：

根据对回归模型方差分析，结果如表7，通过分析，该模型P＜0.01，说明该模型拟合度极显著。 失拟项P＞0.05，说明模型拟合良好，精准度较高。 挂面－挂面恢复系数、挂面－钢板恢复系数、挂面－钢板滚动摩擦系数、挂面－挂面恢复系数*挂面－钢板滚动摩擦系数的P＜0.01，说明以上四因素对挂面的堆积角影响极显著；挂面－钢板恢复系数*挂面－钢板恢复系数、挂面－钢板恢复系数*挂面－钢板滚动摩擦系数0.01＜P＜0.05，表明以上两项对挂面仿真堆积角影响显著。

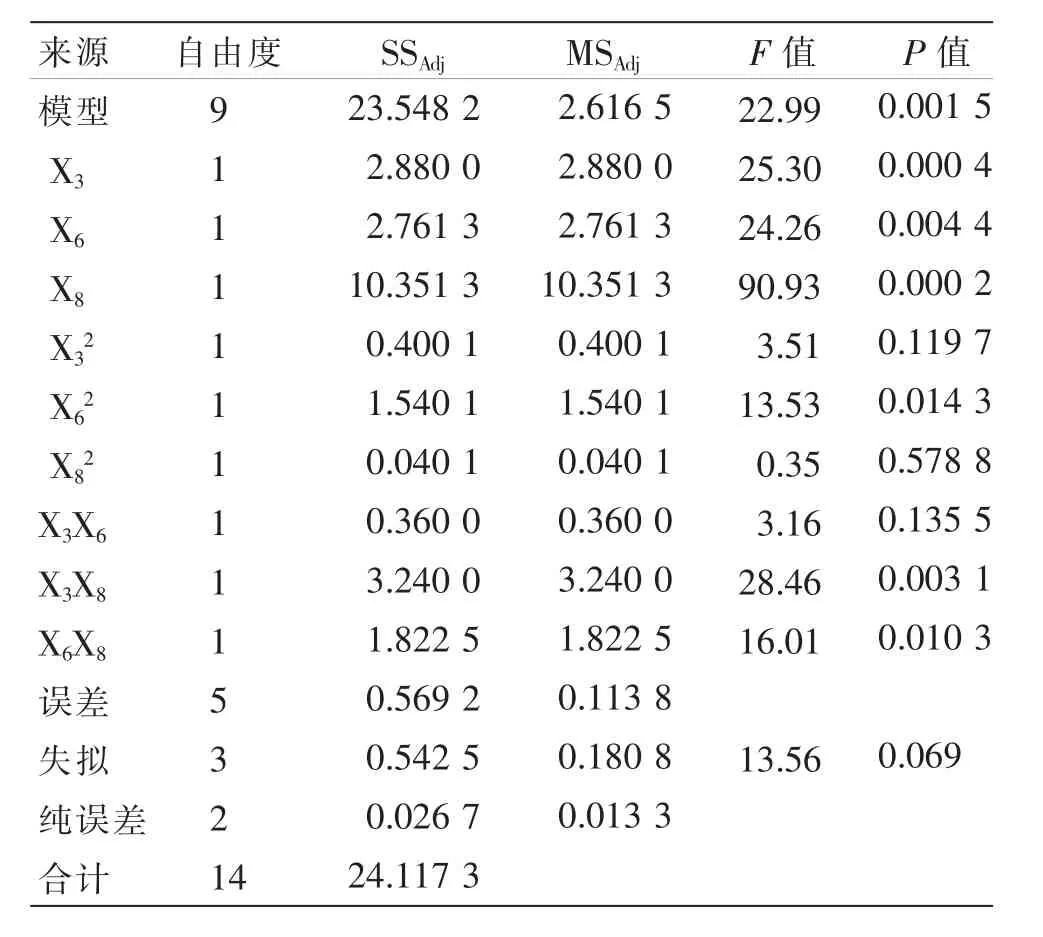
表7 Box-Behnken 实验回归模型方差分析

3.5 标定结果最优参数与实验验证

利用minitab 软件对BB 实验数据进行响应优化， 以物理实验测得的挂面堆积角16.2°作为目标值，得到优化后的挂面－挂面恢复系数为0.270 6，挂面－钢板恢复系数0.319 1， 挂面－钢板滚动摩擦0.0263，响应曲面优化结果如图11。 其余非显著参数取中间水平。 将上述最优值参数代入到EDEM 中进行仿真实验验证。实验测试5 次，分别得到挂面仿真堆积角15.6°、16.3°、15.7°、16.4°、16.1°， 和物理实验测得的挂面的堆积角16.2°。 相对误差为1.1%，证明了挂面参数标定的可靠性， 可为后续细圆挂面堆积运动仿真提供依据。

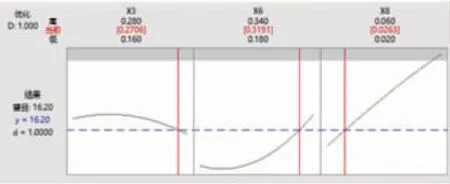
图11 响应曲面优化

4 结论

通过查阅国内外文献确定研究方法， 以物理实验细圆挂面堆积角为响应值， 运用离散元仿真方法对三维建模的挂面进行堆积角的仿真， 利用图像处理技术测定挂面堆积角的角度，并借助minitab 软件进行参数优化方案设计，具体如下：

以物理实验堆积角为响应值， 设计PB 实验确定挂面－挂面之间和挂面－不锈钢之间最显著的接触参数， 最陡爬坡实验确定显著参数的最佳取值范围、BB 实验确定最佳接触参数。 通过响应曲面优化得到挂面－挂面恢复系数为0.270 6，挂面－不锈钢恢复系数为0.319 1， 挂面－不锈钢滚动摩擦系数为0.026 3，其它参数均取中间值。

对最优参数进行仿真， 得到的结果与物理实验误差为1.1%，误差在允许范围内，验证了挂面离散元标定参数的可靠性， 并为细圆挂面离散元仿真提供参数支持。