基于小波分析的智能轮胎磨损和载荷的检测方法
2024-02-22吴金伟陶海涛张峰张士文
吴金伟, 陶海涛, 张峰, 张士文
(上海交通大学 电子信息与电气工程学院,上海 200240)
0 引 言
随着汽车在人们生活中角色的改变,人们对汽车的智能性、舒适性和安全性等都提出了更高的要求,并且伴随着人工智能技术、物联网和5G通信等新兴技术的发展,智能汽车这一概念随即出现。在智能汽车的理念中,将汽车看作是一个与外界环境进行实时交互的系统,智能汽车系统本身需要实时采集汽车与环境的交互信息经分析之后给驾驶员提供良好的辅助作用或用以实现无人驾驶。轮胎作为与环境进行交互的重要媒介,其状态信息本身就是一项非常重要的信息来源[1]。
本文研究所采用的智能轮胎系统主要搭载了三轴加速度传感器和温度压力传感器,使用时,将多传感器系统贴装于轮胎内壁,获取轮胎运行时的胎压信息和胎面振动信息。其中三轴加速度波形是一个典型的时间序列,可采用小波变换的工具对其进行有效分析[2]。由于小波变换具有在时域和频域同时局部化和多尺度分辨的功能,能对时间序列数据进行很好的展开和逼近,通过对加速度时间序列进行小波变换,可以获得时间序列的多尺度信息,并以此实现对原始序列信息的降维,将此特征信息结合胎压、速度信息输入神经网络,可以较为精确地获得轮胎的磨损、载荷信息。
1 轮胎信息采集
本文所设计的智能轮胎系统包括下位机、上位机以及移动终端三个部分,分别对应三个子系统,即下位机、上位机、移动终端,其系统框架与连接示意图如图1所示[3]。

图1 智能轮胎硬件系统架构
图2展示了智能轮胎试验所采集到的三轴加速度原始数据。从图2可以清晰地看到:在非接地区域,三轴加速度数据比较稳定,其中侧向加速度和周向加速度保持在0附近,径向加速度保持在一个较大的非零值附近。在进入接地区域后,三轴加速度的数据都发生了相应的变化,但三向加速度数据变化的情况有着不同的特征,侧向加速度变大,但规律性不明显且变化幅值不大。而周向加速度和径向加速度则出现了明显且有规律的变化。在后续的分析中,本文将主要针对与数值变化更大的z轴径向加速度接地区域。
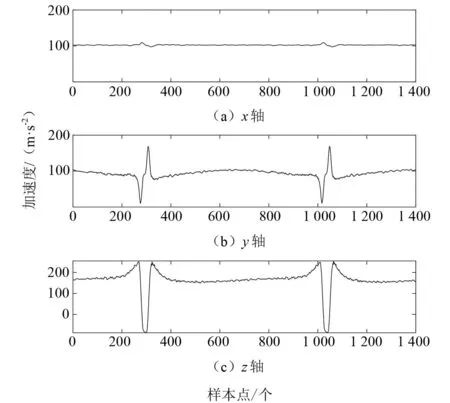
图2 三轴加速度波形
2 小波变换特征采集
本文基于莫尔斯小波进行加速度波形特征的提取。
2.1 莫尔斯小波介绍
广义莫尔斯小波是一系列精确解析小波[4],其分析小波是复值小波,傅里叶变换仅有正实轴。它们可用于分析调制信号,调制信号是具有时变幅值和频率的信号,对于分析局部不连续性也很有用[5]。广义莫尔斯小波的傅里叶变换如式(1)所示。
(1)
式中:U(ω)为单位步长;aP,γ为归一化常数;P2为时间带宽积;γ为摩尔斯小波的对称性,表示莫尔斯小波的时间带宽积和对称性参数影响着小波的形状和小波变换状况。对称性参数γ通过解调偏度控制小波的对称性,时间带宽积的平方根P,正比于小波的时域存续时间。本文的小波变换采用P2=60,γ=3的参数。
2.2 莫尔斯连续小波变换及特征提取
本文所分析的数据是在稳定运行状态下z轴径向加速度波形,对其进行莫尔斯连续小波变换,获得小波系数矩阵,其维度分别代表时间和变换尺度。经过对小波系数矩阵实部、虚部、幅值和相位等指标进行对比,幅值指标较好展示了小波系数的变化规律。图3、图4分别展示了某一运行状态下z轴加速度原始波形及其经小波变换后系数矩阵幅值的情况。
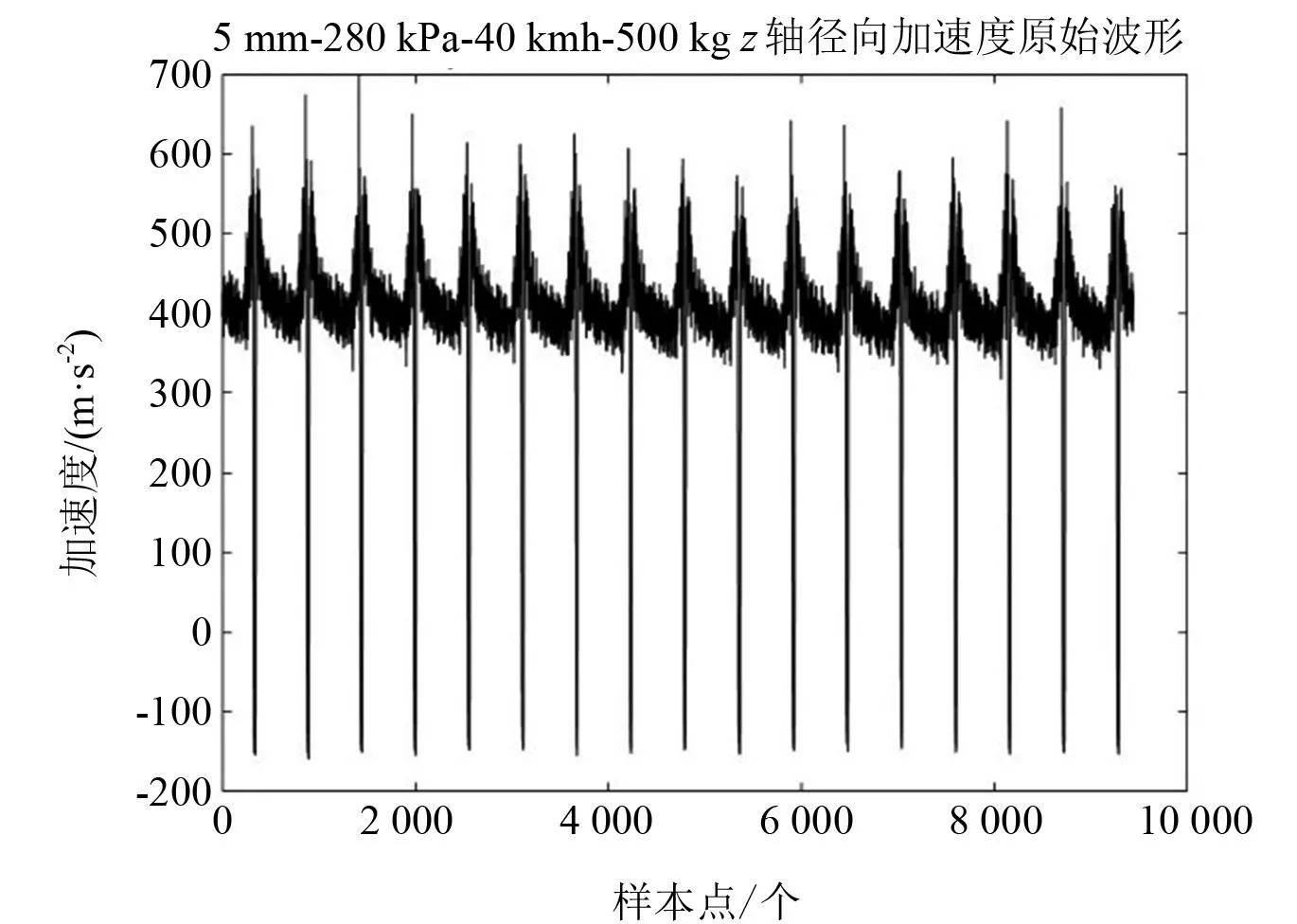
图3 z轴加速度原始波形
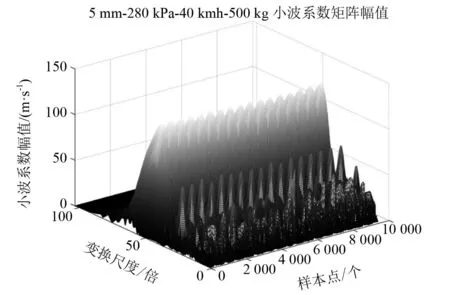
图4 小波系数矩阵幅值
通过对比原始加速度波形和小波系数矩阵幅值,可以发现在轮胎触地时间段,加速度波形发生了剧烈的变化,产生了极短时间的负向加速度,这一现象在小波系数矩阵中也有着较为明显的反映,因此可进一步提取在触地时间对应时刻小波系数幅值随变换尺度的变化情况,如图5所示。

图5 触地点小波系数幅值随变换尺度变化
由图5可知,在相同工况下运行的轮胎,其径向加速度波形经小波变换后在触地时刻所对应系数幅值随变换尺度的变化有着稳定的状态,这一状态可以在一定程度上唯一指定原始波形,实现了原始数据的降维。
依据上述系数幅值随变换尺度波形与原始加速度的唯一绑定,研究在其他条件一致时,胎压、速度、磨损和载荷分别对系数幅值随变换尺度波形的影响。图6~图9分别展示了四种影响因素对系数幅值波形的影响。
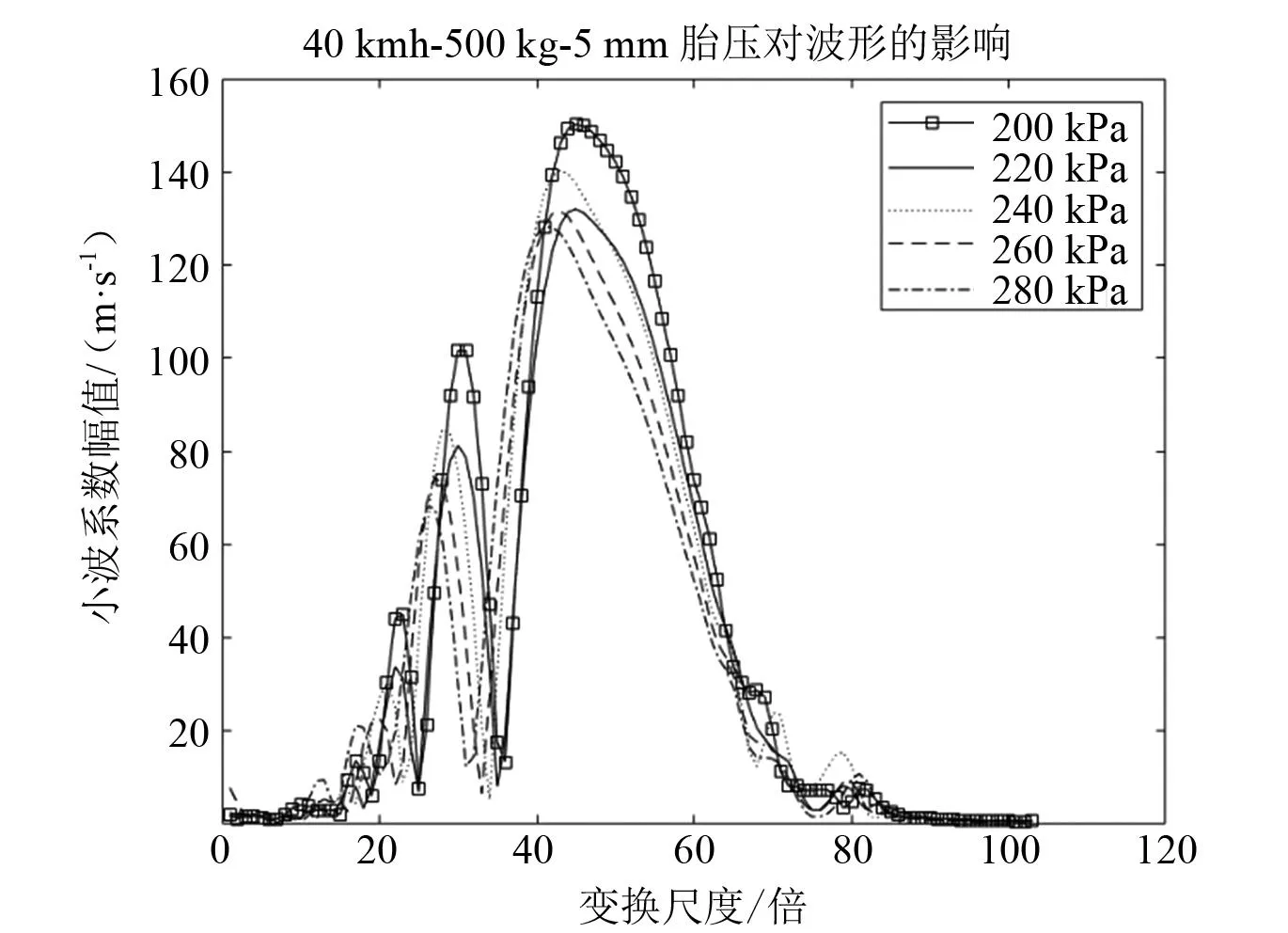
图6 胎压对波形的影响

图7 速度对波形的影响
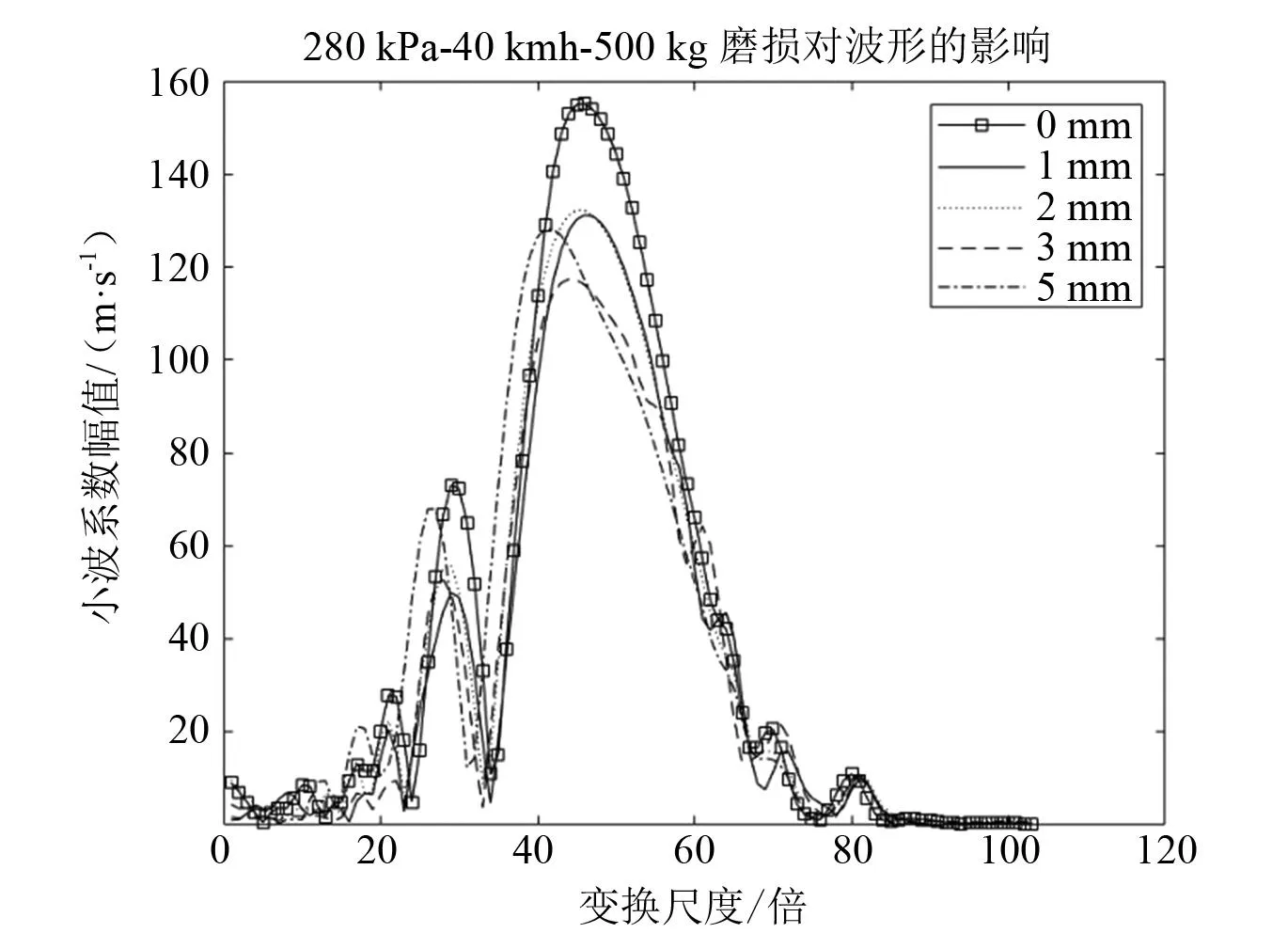
图8 磨损对波形的影响
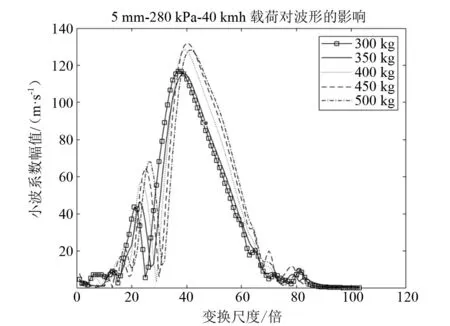
图9 载荷对波形的影响
观察上述四种情况,在保持其他条件一致时,单一因素的变化都会对小波系数幅值随变换尺度波形产生稳定的变化,不同影响因素下的波形图出现了明显的聚类现象,这说明通过小波分析对轮胎状态进行特征提取是可行的。从图中可以看到,除磨损因素对波形峰值的影响是非线性以外,其他因素对波形峰值的影响均可近似线性,且四种因素对极值点的影响也近似线性。四种因素对波形的变化均呈现明显的可区分的现象,因此可将该波形作为特征输入神经网络进行进一步分析。
3 BP神经网络
神经网络具有较强的非线性映射能力,能过够自适应地将学习内容记忆与网络的权值之中,经训练后能够实现对任意非线性函数的模拟,在求值方面有着广泛的应用[6]。
3.1 输入数据预处理
在提取接地处小波系数幅值随变换尺度的变化时,一个采样周期会有多个轮胎运转周期。在中心部位的轮胎运转周期,其时间点两边的数据较多,能够很好地完成较大尺度的小波变换。在采样周期开始和结束时的轮胎运转周期,其进行较大尺度的小波变换时两侧数据点不够而引起小波系数幅值随变换尺度波形产生畸变,因此需要剔除此类非典型波形。
此外,由于接地处加速度波形发生的突变即是本文研究的主要对象,而一般的降噪处理方法会将此种突变看作是一种噪声进行处理,使得突变程度有所缓和,且缓和的影响不可控制,因此不适合对加速度波形在进行小波变换前进行降噪处理。这在很大程度上保证了小波变换所获波形的稳定性,但是导致了小波变换较小尺度的部分受到噪声的影响比较大,前10个变换尺度的波形较为杂乱。
为解决上述问题,在提取接地处小波系数幅值随变换尺度的变化时,不提取每个采样周期首尾两个接地处小波系数幅值波形,将其余符合条件的波形提取变换尺度为11~100共90个尺度的部分求取平均值,得到平均波形,然后剔除与该平均波形相关系数小于0.99的波形,循环迭代,所有提取波形与平均波形的相关系数都在0.99以上,保证数据的可靠性。
3.2 神经网络搭建
数据的输入设定如表1所示,为小波系数幅值向量和胎压、速度合集。

表1 神经网络92维输入
轮胎磨损、载荷作为输出,则BP神经网络的输入维度为92,输出维度为2。隐含层节点数根据式(2)先确定大致区间。
(2)
式中:m、n、k分别为输入、输出和隐含层节点数;a为取值1~10之间的整数。对区间内点逐一训练和比较,以获得最高精度下的隐节点数,本文隐含层取16个节点。最终确定的网络结构如图10所示。
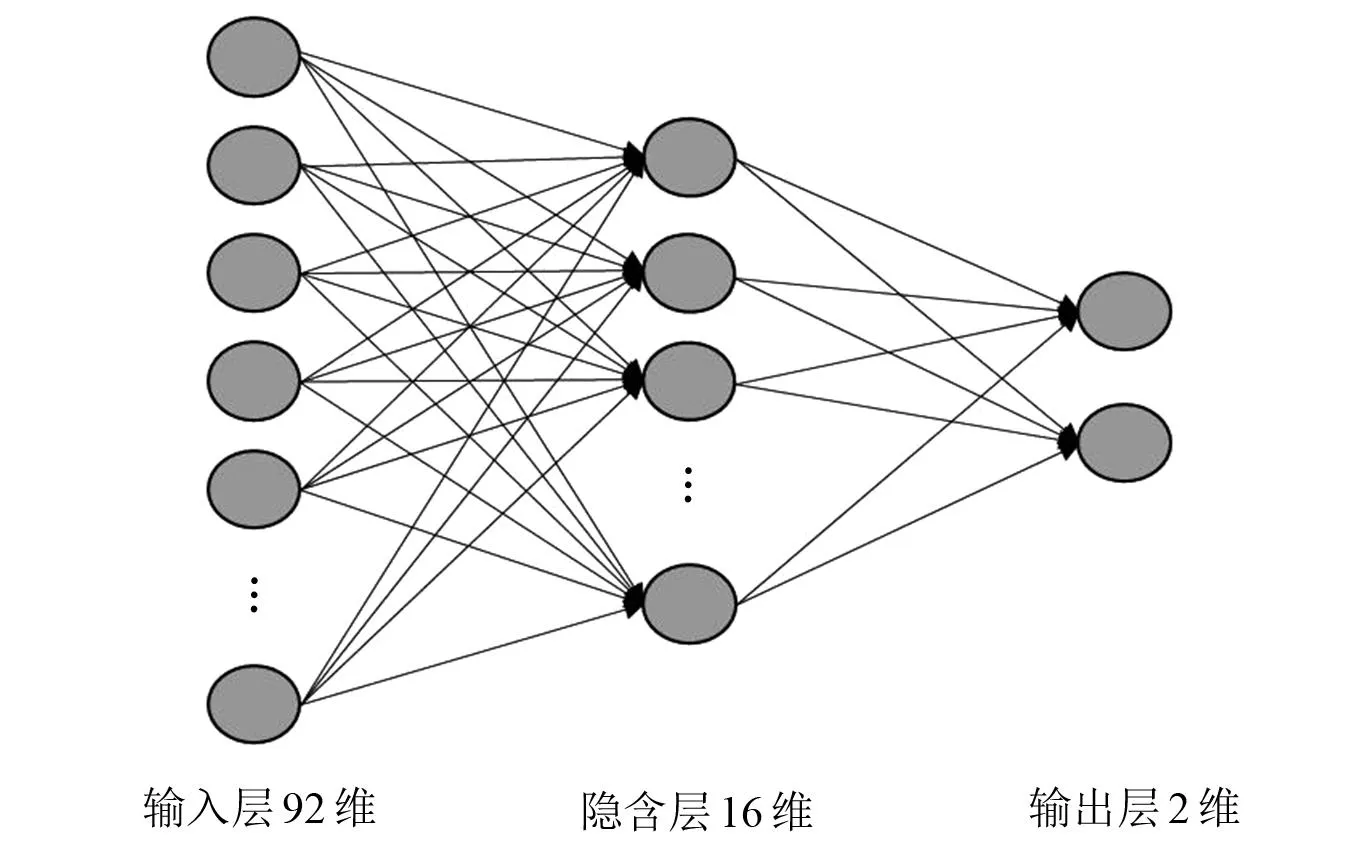
图10 神经网络结构
4 试验结果
将经过预处理的数据按3∶1∶1分为训练集、测试集和验证集。在训练结束后,验证集上的也取得了较好的结果,如图11、图12所示。

图11 磨损预测结果
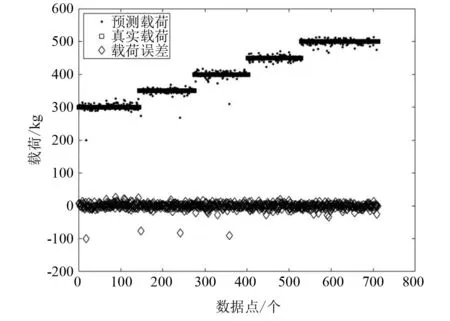
图12 载荷预测结果
从以上验证集的预测结果可知:在磨损误差0.3 mm、载荷误差12 kg以内的算法的预测结果都能够在90%以上的情况下预测准确;在磨损误差0.5 mm,载荷误差20 kg以内,算法的准确性达到了98%以上。
在实际应用中,磨损和载荷均是一个相对稳定的量,其预测结果围绕真实值在一定范围内波动,因此可采用统计方法获取更精确的结果。可将当前时刻前一段时间内的预测结果的均值作为当前时刻的结果,可有效提高精度。
5 结束语
本文设计了一种基于小波分析筛选轮胎加速度特征的方法,实现了轮胎原始加速度波形的降维,获得加速度波形接地处小波系数幅值随变换尺度的变化向量。将其和胎压、速度等易测量共同作为神经网络的输入,使用三层简单神经网络,即得到了良好的测量结果。
