面向制造业智能工厂的AGV作业效率与逻辑策略研究

单芝庆

〔常至智能科技(无锡)有限公司,江苏 无锡 214000〕

0 引 言

随着5G的全国普及,工业互联网推动了制造业的发展,降低成本、提高工厂工作效率也成了人们比较关心的问题。搬运、输送作为大型智能工厂生产的重要一环,在其中已广泛地应用AGV技术[1-2]。通过查阅文献,了解到智能工厂AGV作业效率的提高可以从AGV系统调度策略上进行优化和改善。AGV作业效率的提高可以减少生产过程中的等待时间和资源浪费,从而提高生产效率和降低生产成本;而AGV逻辑策略的优化可以提高其自适应和智能化水平,从而适应不同的生产场景和需求。

在现有技术的基础上提出了改进的粒子群算法可以有效地优化制造业智能工厂AGV的调度策略,提高智能工厂AGV的作业效率[3]。 本文提出的AGV系统调度优化策略不仅可以应用到制造业生产运输上,而且也可以推广到所有需要搬运的领域,具有较强的实用价值。

1 AGV系统调度策略的优化

1.1 AGV系统调度问题的分析

通过对制造业某智能工厂的AGV系统使用情况的调查发现:AGV工作一般按照AGV系统下达时间的先后顺序进行排列,AGV系统先统一给每台AGV分配作业;作业的排序只与时间先后有关,与AGV所在位置无关[4]。

但由于AGV在具体工作时会受到环境和自身电量等因素的影响,存在未能按照预测的时间完成任务,或者已分配任务在计划中不是最优分配等情况,AGV的利用率就会大大下降[5]。为了提高AGV作业的效率,降低生产成本和时间,本文旨在优化AGV系统作业时间,采用改进的粒子群算法寻找最佳的AGV调度顺序,以提高系统作业效率[6]。图1为AGV调度系统图。

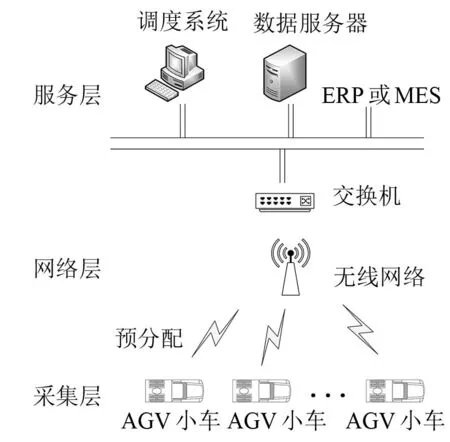
图1 AGV调度系统图

1.2 数学模型的建立

假设AGV系统中的AGV数量是已知的,各个取货位置、放货位置的距离已知,各台AGV品牌和型号相同且已知。为了优化AGV系统的作业效率,需要将AGV系统作业的最短总时间设定为目标函数,而针对不同的AGV作业时间对AGV分配的影响,AGV运行时间、装载时间以及卸载时间等因素对AGV系统作业总时间的影响也需要进行分析[7]。基于此,建立如下数学模型,以解决AGV作业效率优化问题。其中设AGV系统中共包含M台AGV,有N个作业站点,在一个周期T内可以执行Z个作业。

式(1)为目标函数,表示AGV系统完成所有作业的最短总时间。

(1)

式中:tij为第i台AGV做第j个作业所用的时间;ti(j-1,j)为第i台AGV在做完第j-1个作业后到第j个作业的起始位置所用的时间;Uij为第i台AGV的第j个作业装载时间;Wij为第i台AGV第j个作业卸载的时间;Xij为第j个作业是否由第i台AGV作业。

式(2)是目标函数的约束条件,表示一个作业只能由一台AGV来完成。

(2)

式(3)是目标函数的约束条件,表示AGV系统完成的作业为下达的所有作业,所有动作受系统控制。

(3)

式(4)是目标函数的约束条件,表示所有AGV完成作业必须在一个周期T内。

(4)

式(5)是目标函数的约束条件,表示AGV从本次作业的起始位置到本次作业的终止位置所用的时间。

(5)

式中:Sij为第j个作业的装载和卸载间的距离;Scj为第j个作业的装载和卸载间的转弯距离;Vs为AGV在直线行走时的速度;Vc为AGV在转弯行走时的速度。

式(6)是目标函数的约束条件,表示AGV从上次作业的结束位置到本次作业的开始位置所用的时间。

(6)

式中:SS(j-1,j)为第j-1个作业位置到第j个作业位置的直线路程;SC(j-1,j)为第j-1个作业位置到第j个作业位置转弯路程。

式(7)是目标函数的约束条件,表示本次作业的预计完成时间。

Tij=Ti+tij+ti(j-1,j)

(7)

式中:Tj为完成第j个作业的规定时间;Ti为第i台AGV完成本次作业的预计时间。

式(8)是目标函数的约束条件。

Tij≤Tj

(8)

式(9)是目标函数的约束条件,表示每个作业必须只能由一台AGV完成,若第j个作业由第i台AGV完成,则值为1,否则为0。

(9)

在构建了AGV的作业数学模型后,可将该模型用于AGV系统作业分配的计算中,对于智能工厂AGV作业效率与逻辑策略的研究有很大的价值。

2 粒子群算法的改进和实现

本文选用改进的粒子群算法不仅收敛速度快、简单高效而且参数和算力较少,可以有效地减少AGV系统的时间,提高工作效率[8]。

粒子群算法中所提到的粒子没有质量且仅有两个属性:速度V和位置X,速度是矢量[9],包括速度大小和方向,位置表示粒子当前所在的坐标。

Vid=ωVid+C1random(0,1)(Pid-Xid)+
C2random(0,1)(Pgd-Xid)

(10)

式中:Vid为粒子的速度;Xid为粒子当前的位置;ω为惯性因子;C1、C2为常数,分别表示粒子的个体认知因子和群体认知因子;random(0,1)为区间(0,1)上的随机值;Pid为第i个粒子个体极值的最优解;Pgd为整个粒子群体的全局最优解。

本文所使用的改进的粒子群算法是在基本的粒子群算法的基础上进行改进的,具体改进如下。

(1)Vid改进:先对每一个粒子的极值进行改进,如式(11)所示。

Pr=(Pr1,Pr2,…,PrD)

(11)

其中:Prj=(P1j+P2j+…Pnj)/n,j=1,2,…,D

(2)Pid改进:在第t次的更新过程中,随机产生一个区间(0,1)的随机数r,按公式Ri=t/Gmax得到Ri,Gmax为最大更新次数。 若r>Ri,任意选择一个粒子,则该粒子的最佳位置为Prnd,将其取代式(12)中的Pgd,按式(12)更新。

Vid(k+1)=ωVid(k)+C1random(0,1)[Prd(k)-Xrd(k)]+
C2random(0,1)[Prnd(k)-Xid(k)]

(12)

式中:k为当前更新次数。Prnd从其他粒子的Pi中随机选择,且与Pg不相同。

AGV系统的调度比较复杂,总的来说是分配给各台AGV作业和每台AGV对于已分配给自身作业的顺序[10]。本文对多AGV调度的粒子群算法在三维空间中进行设计。

作业分配完成后,AGV调度系统会以该作业的终点作为下一次作业的起始点,对其他作业进行预分配。改进的粒子群算法如图2所示。

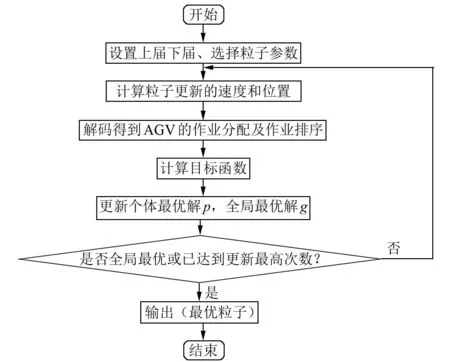
图2 改进的粒子群算法流程图

3 试验分析

3.1 某一时刻AGV作业分配数据分析

本文在进行AGV作业分配中,通过把AGV作业最短的总时间作为目标,利用MATLAB软件对模型进行求解,得到各台AGV作业分配的次序。

假定个体认知因子C1=2,群体认知因子C2=2,惯性因子ω=0.6,最大迭代次数Cmax=200,作业总数Z=22,AGV总数M=8,粒子群总数D=40,运算精度为0.6。AGV系统在某一时刻的作业分配如表1所示。

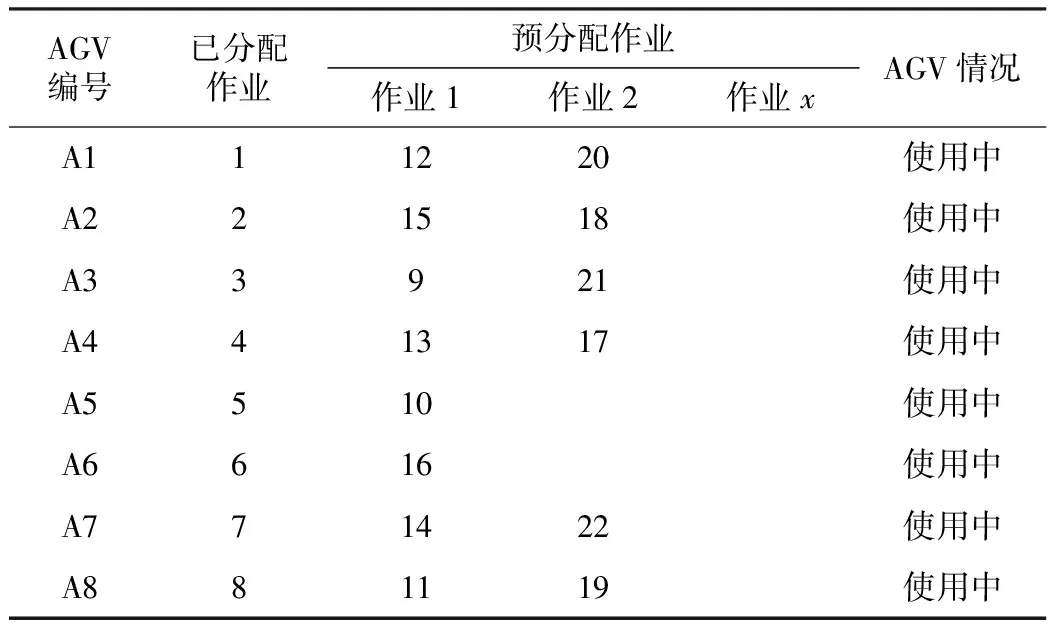
表1 某一时刻AGV作业分配数据表

通过分析表中数据,可以清楚地看到AGV的工作任务及状态,然后系统会进行不停地更新,从而使AGV能顺利地完成作业。

3.2 优化前后AGV作业能力对比

本文结合某智能工厂的辅料运输实际工作情况,利用改进的粒子群算法对优化前后AGV系统作业能力进行计算分析,用搬运能力代表AGV的作业能力[11]。表2是优化前各台AGV作业能力统计,表3是优化后各台AGV作业能力统计,时间单位为秒。

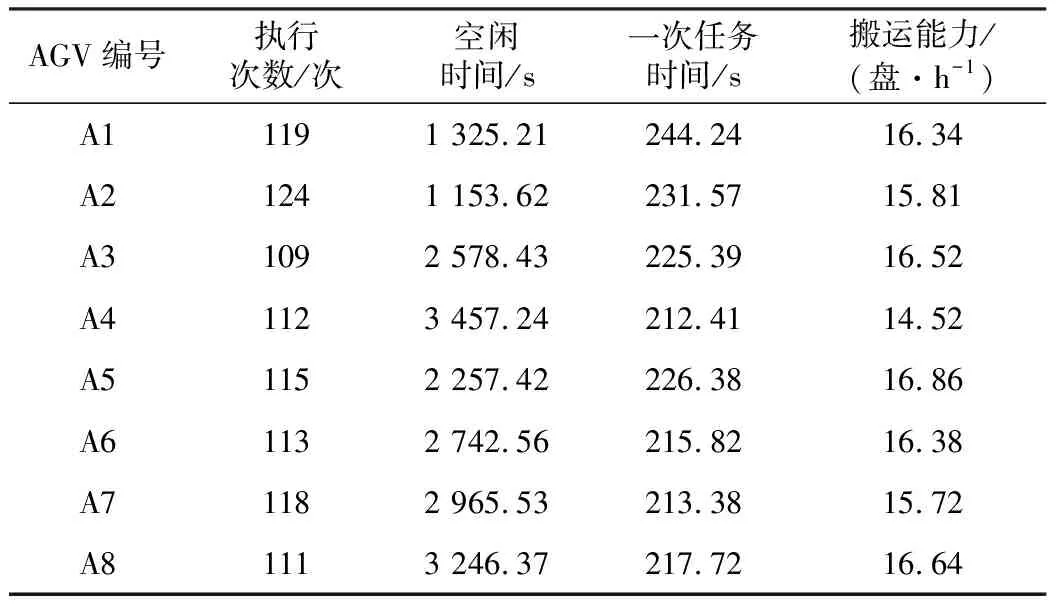
表2 优化前各台AGV作业能力统计

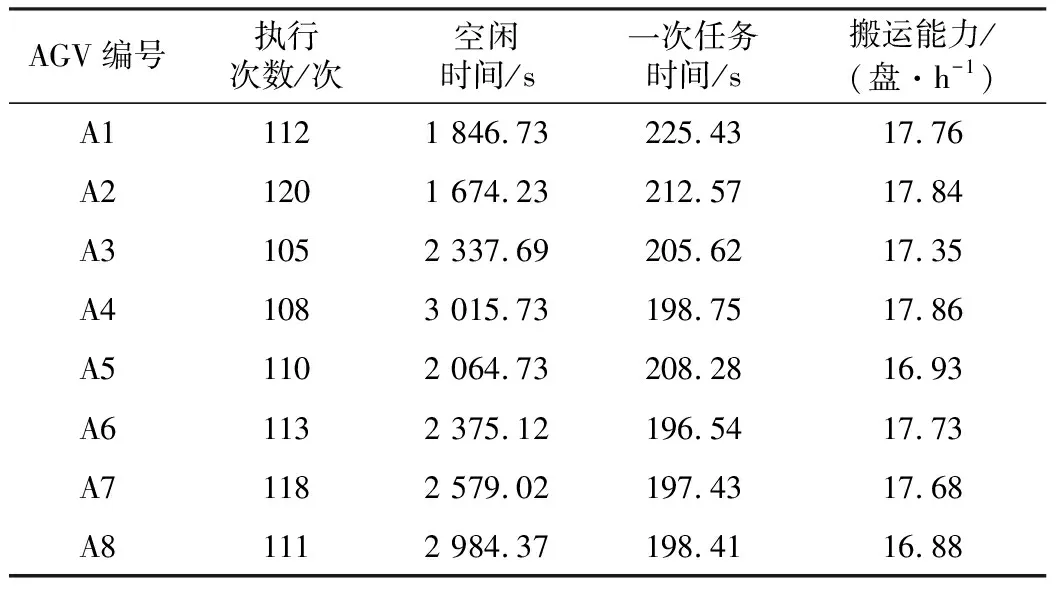
表3 优化后各台AGV作业能力统计

根据表2和表3优化前后各台AGV能力统计绘制折线统计图,使两者的对比更加清晰,如图3所示。

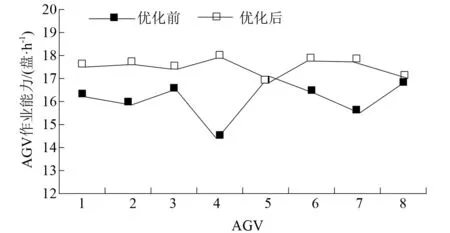
图3 优化前后各AGV能力对比

通过比对优化前后AGV的作业能力,可以得出结论:优化前平均每台AGV的作业能力为16.10盘/h,而经过优化后,这一能力值提高到了17.50盘/h。相比之前的作业能力,优化后的作业能力提高了8.73%,明显地提高AGV系统的作业效率。

4 结束语

本文通过调用某智能工厂的辅料运输的AGV系统的工作数据,利用改进的粒子群算法对AGV系统进行优化,使用MATLAB软件对模型进行求解,将AGV系统作业最短的总时间作为目标进行分析,采用预分配的方法提高AGV的工作效率[12]。该方法经过对比分析优化前后各AGV作业能力的情况,比较直观地看出优化后的作业能力比优化前的作业能力提高了8.73%,为提高AGV作业效率提供了一种可行方案。