含分布式电源及储能系统的配电网最优配置研究
2024-02-22苏义荣李怀良
苏义荣, 李怀良
(国电南瑞科技股份有限公司, 江苏 南京 211106)
0 引 言
目前,在配电网中接入电池储能系统(battery energy storage system, BESS)和分布式发电(distribution generation,DG),不仅有利于提高电力系统的效率[1],还可以改善电压分布、减少技术功率损失、缓解拥塞、网络扩展延迟和提高可靠性[2]。此外,由于对全球变暖的日益关注,减少碳排放受到了广泛的关注[3],现有的可持续发展、绿色能源政策鼓励使用可再生的DG和BESS。
针对BESS和DG,配电公司面临两大挑战。第一个挑战是BESS的最优位置和容量大小,错误的配置会降低BESS和DG的优势,例如能量损失、电压控制、电压偏差缓解以及电能质量改善[4-6]。第二个挑战是BESS的最优调度问题,配电公司可以通过优化BESS运营来提高能源的利润[7]。
从配电网建模角度,配电网中BESS和DG的最优积分模型本质上是一个混合整数非线性模型(mixed-integer nonlinear model,MINLM),因为系统的运行状态是由非线性潮流方程决定的 ,投资决策是由整数变量表示的[8]。文献[9]提出了一种粒子群优化算法来解决主动配电网中的协调BESS和DG规划。规划的目标是在网络安全运行的前提下,保障分布式系统的利润最大化,减少投资和运营/维护成本。文献[10]提出了一种规划DG和BESS的两步骤方法。第一步解决了系统的容量问题,第二步解决了位置规划问题,以最小化有源功率损失来改善电压分布。文献[11]提出了一个分布式优化框架以解决微电网中的BESS和DG容量规划。
分布式发电以及储能技术进步迅速,中低压配电网中的BESS和DG接入量在不断增加,亟需在设备配置过程中进一步提高利润和减少网络损耗。针对这个问题,本文提出了一种混合整数非线性规划模型,基于Zbus矩阵模型,并利用模拟退火算法结合规划-运行分解方法进行求解。
1 混合整数非线性规划模型
1.1 目标函数
基于Zbus矩阵,本文提出BESS和可再生DG的最优位置选择和运行问题的数学模型,该模型是一种单目标混合整数非线性规划模型。
(1)
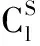
1.2 约束条件
MINLP模型的约束条件如式(2)~式(27)所示。式(2)、式(3)分别为有功、无功平衡。式(4)为网络中的ZIP负荷模型。
(2)
(3)
(4)
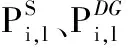
式(5)和式(6)利用Zbus矩阵计算母线电压的实部和虚部。基于系统母线电压的叠加原理。母线电压取决于两种不同类型的电源:配电变电站的指定输入母线电压、负载、电容器、可再生DG和BESS产生的电流注入。式(7)和式(8)定义变电站电压的幅值和角度。式(9)和式(10)利用基尔霍夫定律计算变电站节点电流的实部和虚部。
(5)
(6)
(7)
(8)
(9)
(10)
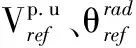
式(11)定义了安装DG提供的有功功率。式(12)将BESS的充电和放电功率视为两个不同的变量。式(13)表示BESS的荷电状态,该约束考虑了BESS的充放电效率和自放电率。式(14) 、式(15)分别为BESS的初始电荷状态和最终电荷状态。式(16)、式(17)为限制安装的BESS的注入功率和释放功率。式(18)为BESS的容量限制。式(19)用于限制节点i处的BESS运行状态的变化次数。
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)

式(20)~式(23)为网络的运行限制条件;式(20)为变电站的发电容量限制条件;式(21)为线路中的最大电流限制条件;式(22)为变压器最大视在功率限制条件;式(23)为两个网络节点的电压限制;式(24)、式(25)限制网络中安装的BESS和DG的数量;式(26)、式(27)确保同一位置只安装一个装置。
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
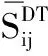
式(1)~式(27)中描述的数学模型是非线性且非凸的,这是由于基尔霍夫定律方程中的变量相乘,以及ZIP负载模型的恒定阻抗项中存在电压平方。
2 解决方案
如前所述,优化问题是一个混合整数非线性规划模型,为了进行求解,提出了一种规划-运行分解方法。该方法将MINLM划分为两个相关的优化问题。分别负责在配电系统中BESS和DG的位置规划问题和BESS运行状态问题。
为了解决规划问题,本文使用了SA算法,该算法定义的邻域结构,具有跳出局部最优解的优点,使用基于Zbus矩阵的灵敏度分析。为了解决BESS运行状态问题,本文提出一种分解方法,以较低的计算量保证近似全局最优解。提出的分解方法包括两个步骤:第一步解决了一个宽松的优化问题,该问题暂时从系统中移除电气变量,并获得最佳BESS操作;第二步,基于Zbus-Gauss方法,将从松弛优化问题中获得的BESS充放电协调方案视为潮流中的功率注入和消耗(PQ节点),以获得系统的实际运行状态。
读取系统数据并构建Zbus矩阵,包括初始温度(充分大)、温度下限(充分小)、初始解状态(算法迭代的起点)和迭代次数。冷却方法的计算如上所述,从SA算法开始。然后,使用基于Zbus矩阵的灵敏度因子,从邻域结构中获得SA算法的新解。运行阶段使用为规划阶段找到的新解来寻找BESS的最佳运行状态。在这一步中,使用所提出的分解方法来求解系统的运行状态以及考虑可再生DG的BESS的最优运行状态。
然后,规划阶段使用获得的数据来计算新解的适应度函数。其次,SA算法的随机机制控制解之间的变换。新配置的接受遵循以下标准:始终接受成本降低的解决方案,而成本较高的解决方案可以接受或不接受,并具有一定的概率。
(28)
如果新的解优于当前解,则更新现有解。重复此过程直到到达Nk。对于下一个温度水平,通过冷却方案更新Tk和Nk。当达到停止标准时,程序结束,并给出找到的最佳解决方案。图1为规划-运行方法流程。
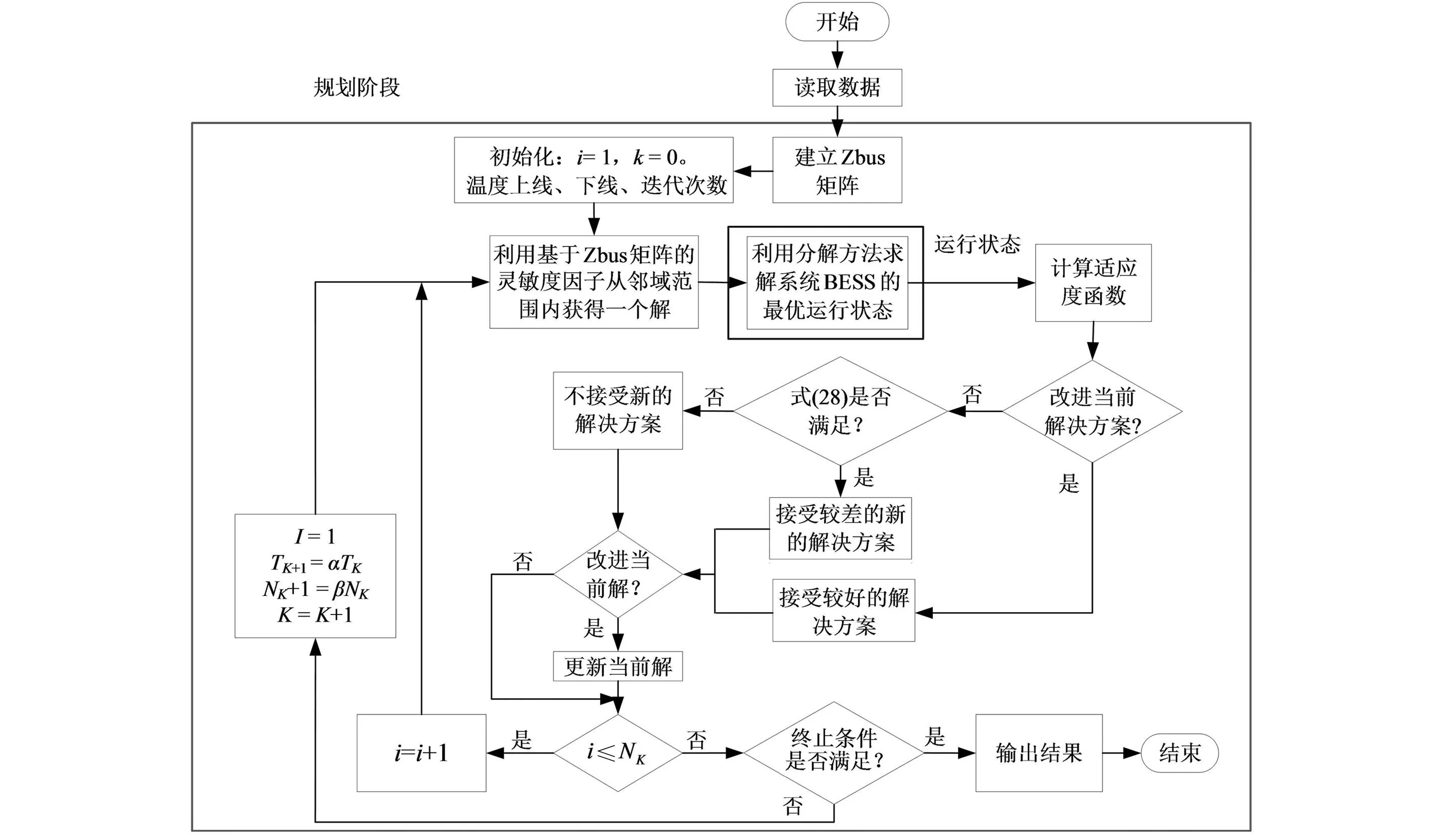
图1 规划-运行分解方法流程图
3 仿真系统测试
230节点中低压测试配电系统集成了一次二次网络。中压电网有92个节点、2个变电站和91条一次馈线。低压网络有138个节点、32个变压器和106个次级电路。为了可视化真实的综合配电系统,一次和二次网络分别为图2和图3。图中:变电站用正方形表示;黑点是主节点;白色圆圈是次要节点;带有变压器的节点由黑色三角形表示。图4、图5中的黑点是两个网络共享的节点。

图2 测试系统主网络
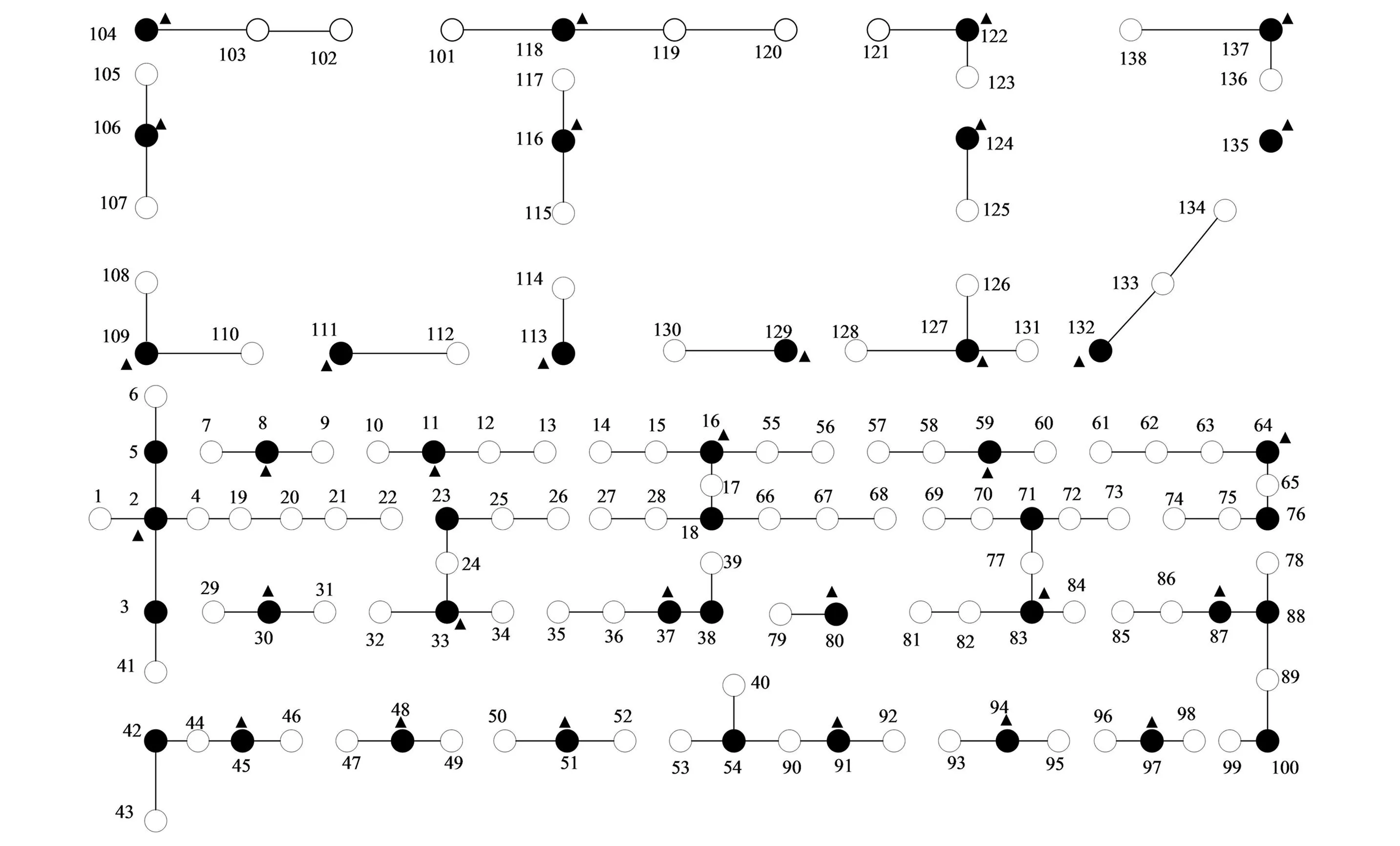
图3 测试系统二次网络

图4 每小时负荷曲线

图5 每小时典型光伏发电曲线
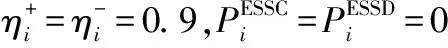
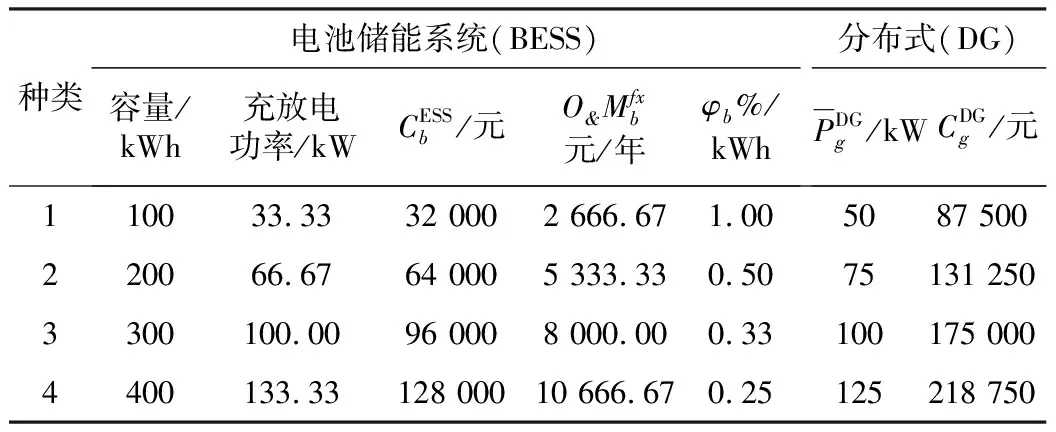
表1 电池储能系统和分布式发电相关信息
设置功率300 kVA、一次网络和二次网络的标称电压为系统的基准值。可再生DG安装的候选节点如表2所示,BESS安装的候选节点是中压网络的所有节点。

表2 可安装DG的候选节点
4 仿真测试结果
SA算法的参数化是一种典型的启发式算法通过调整参数优化冷却的过程。所使用的冷却方案系数为μ=0.4%,Φ=5%,β=1.1和α=0.95。初始迭代次数N0=230,初始解决方案的成本|F(x0)|是1 361.69万元,T0为初始温度。算法终止的两个标准是:冷却温度最终为60 ℃;如果未达到最优解,设置为15 ℃。
在Intel©Core i5-4460S 12 GB RAM PC中,使用MATLAB(2020b)和GAMS之间的接口实现规划操作分解方法。使用解算器CPLEX(版本12.6.2.0)求解运行方式阶段分解方法的LP模型。为了证明所提出方法的有效性和可靠性,研究了四个案例:① 不含BESS和可再生DG;② 仅含可再生DG;③ 仅含BESS;④ 含BESS和可再生DG。在第4节所述的实际中低压配电系统上对所提出的规划运行分解方法进行了测试。案例2~4的CPU时间分别为12 974.84 s(3.6 h)、9 678.99 s(2.69 h)和21 973.37 s(6.10 h)。
电池储能系统的安装、运行和维护成本如表3所示。对比案例1和案例2的结果,扣除投资成本后,能源套利收入约为0.36%。当仅安装BESS时(案例3),与案例1相比,获得的收入约为6.76%。安装了BESS和DG(案例4),与案例1相比,获得的收入约为7.12%。BESS的案例获得的收入较高,这是因为通过在电价较低的时间向BESS充电,在电价较高的时间放电,从配电变电站购买能源的总成本降到了最低。如果不考虑投资成本,案例2、3和4的能源套利利润将更高(约为18.67%、29.25%和47.93%)。然而,尽管投资成本很高,但从安装这些设备中获得的经济效益充分证明了投资的合理性。此外,也最小化了网络的损失。比较案例1和案例2的中、低压网络中的电能损失,安装可再生DG时,最小值约为2.79%。当仅安装BESS时(案例3),与案例1相比,中、低压网络中的损失减少了约1.25%。在这种情况下,案例2比案例3更优,因为BESS运行需要从电网吸收电力。
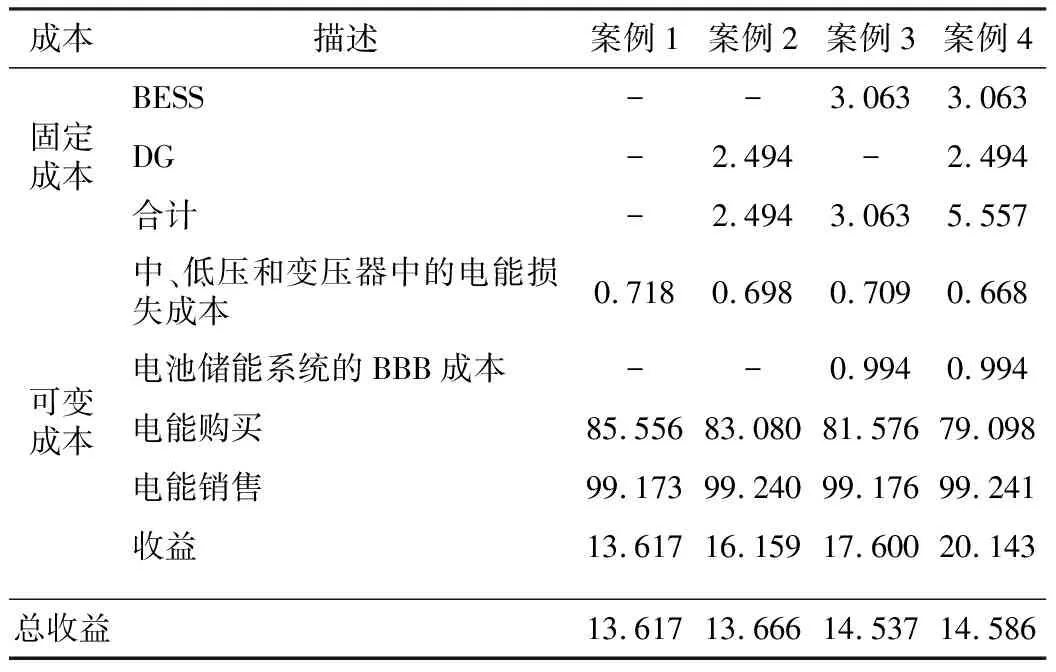
表3 电池储能系统的安装、运行和维护成本
当安装BESS和DG时(案例4),中、低压电网中的损失比案例1减少了4.14%。最后,案例4表明,最大化从能源套利中获得的收入、扣除投资成本和最小化网络损失的更好选择是同时考虑BESS和可再生DG。虽然这些设备的安装成本很高,但获得的利润将更高。
图6为四种情况下DG和BESS影响了变电站输出的有功功率。案例1和2在第20 h获得的峰值功率为10.498 MW,案例3和4在第22 h获得的峰值功率值分别为9.142 MW和9.141 MW。在这两种情况下,使用BESS获得的新峰值功率降低约12.92%。
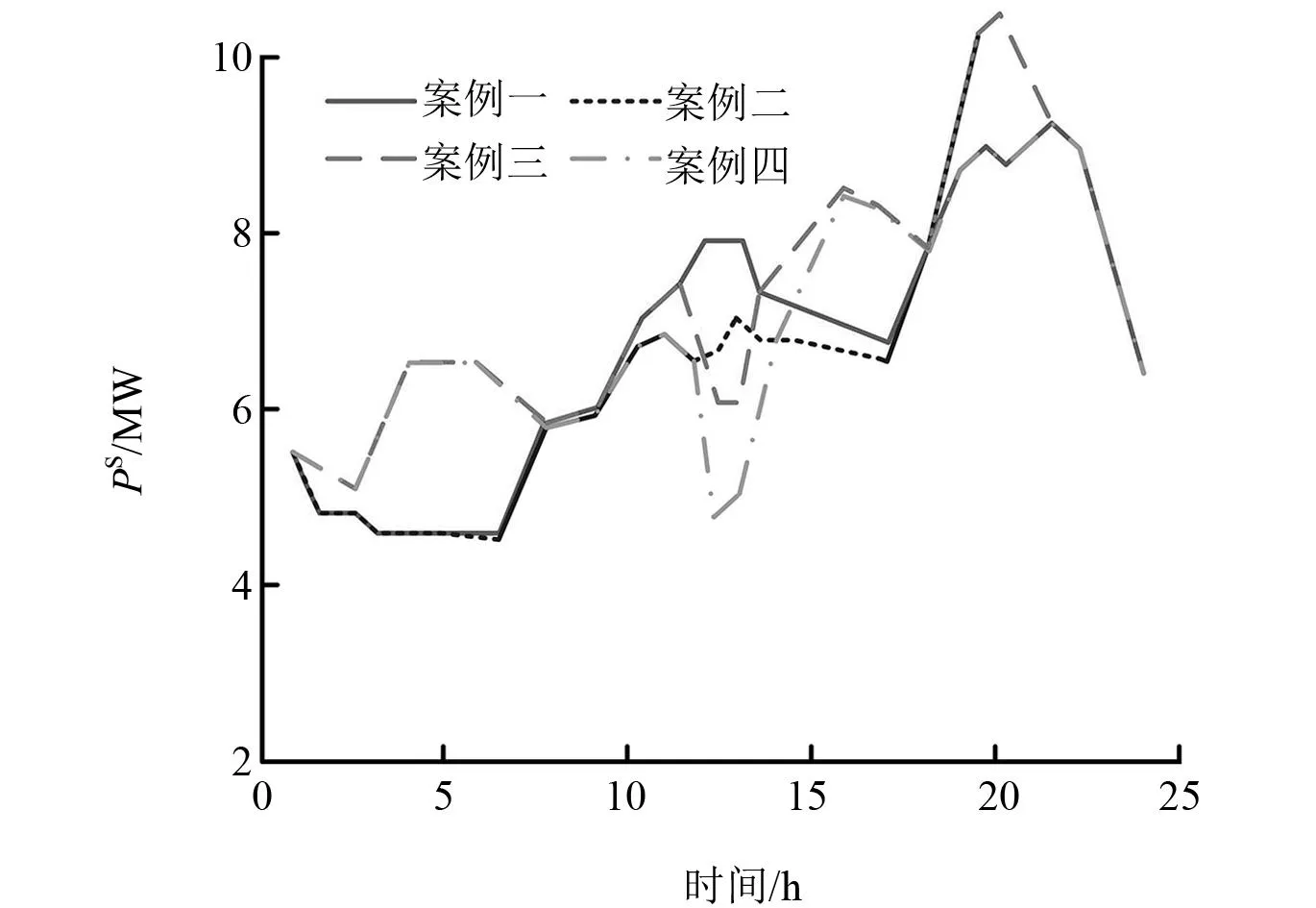
图6 变电站有功功率
表4为在案例3和案例4情况下安装BESS的中压节点。对于这两种情况,得到了相同的BESS安装位置和类型。表5为案例2和4安装了可再生DG的低压节点。对于这两种情况,得到的DG位置和类型都是不相同的。原因是案例4比案例2多加入了BESS系统,改变了配电网的电压和电流流动情况,能够在低价时进行储能,在电价较高时进行放电。
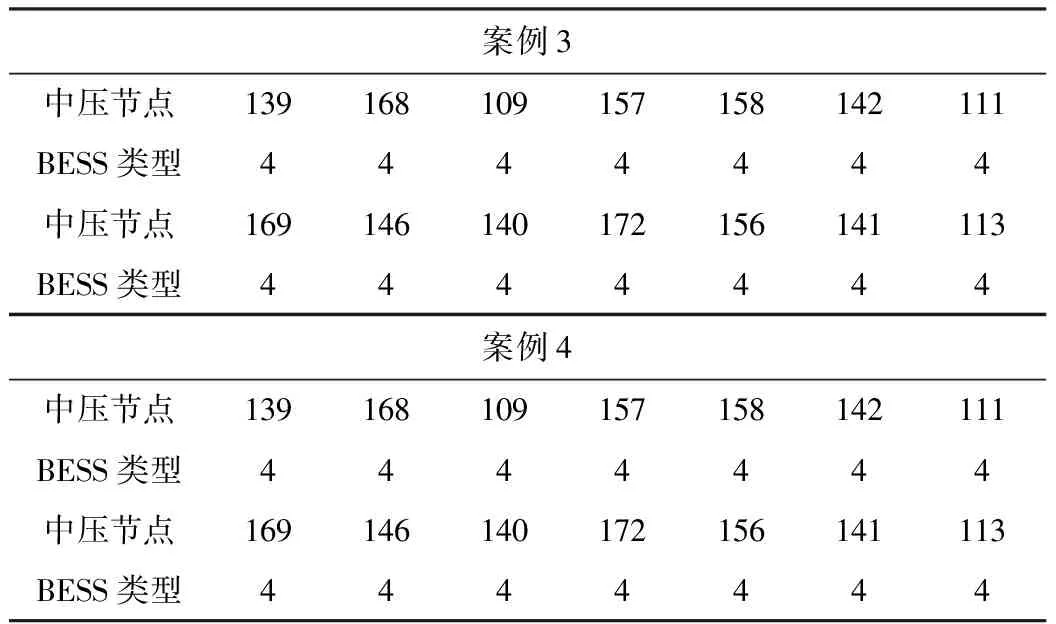
表4 案例3、案例4中安装能源管理系统的中压节点

表5 案例2、案例4中安装分布式电源的低压节点
5 结束语
本文提出了一种解决的方法配电系统中BESS和可再生DG的最佳位置配置和运行状态。最初的混合整数非线性规划问题被划分为两个相关的优化问题,使用规划-运行分解方法进行求解。在规划阶段,采用基于Zbus矩阵的SA算法来解决BESS和DG的位置问题。利用一种求解BESS运行状态的两步分解方法,第一步解决了一个宽松的优化问题,从系统中移除电气变量,获得最佳BESS操作;然后,在第二步中,基于Zbus-Gauss方法,将从松弛优化问题中获得的BESS充放电协调方案视为潮流中的功率注入和消耗(PQ节点),以获得系统的实际运行状态。
利用230个节点的配电系统对规划运行分解方法进行了测试和验证。结果表明,本文提出的方法在扣除投资成本后,可以显著减少能源损失,并改善从能源套利中获得的收入。同时配电接入BESS装置优化了发电容量曲线,减少网络损耗,降低变电站输出功率的峰值。
