基于高斯-柯西变异帝国竞争算法的微电网优化调度

陈海旭, 余畅文, 卢银均, 陈磊, 马小龙, 刘闯, 刘炬

(1.三峡大学 电气与新能源学院,湖北 宜昌 443000;2.国网福建省电力有限公司福州供电公司,福建 福州 350000;3.国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000)

0 引 言

近年来,以可再生能源为主的微电网系统得到了快速发展,但微电网技术尚不成熟,微电网供电可靠性、能源利用率和运行成本等都是目前亟待解决的问题[1-2]。因此,对微电网优化调度进行研究,提出合理可行的微电网调度策略具有重要意义。文献[3]为了麻雀搜索算法的优化性能,利用反向学习和自适应分布策略对麻雀搜索算法改进,以微电网运行成本为目标函数,提出了一种基于改进麻雀搜索算法的微电网优化调度模型。文献[4]为了平衡微电网的环保性和经济性,在微电网优化调度模型中引入了具有碳捕获能力和弃光弃风消纳的电转气系统,采用新型生物地理学优化算法对模型进行了求解,验证了模型的可行性和算法的优越性。文献[5]采用差分进化策略对黑洞算法进行改进,以燃料电池和蓄电池充放电功率为优化向量,以微电网运行成本最低为目标函数,建立了基于改进黑洞算法的微电网优化调度模型,采用实际算例验证了模型的正确性和实用性。微电网结构复杂,系统内分布式电源种类和求解方法均会对其优化调度结果产生一定影响,因此微电网优化调度模型和求解方法还有待进一步研究。

基于此,本文以微电网综合运行成本最小为目标函数,建立基于高斯-柯西变异帝国竞争算法(Gaussina-Cauchy imperialist compertitive algorithm,GCICA)的微电网优化调度模型,采用实际算例对模型的正确性及求解方法的优越性进行验证。

1 微电网优化调度模型

1.1 目标函数

以微电网综合运行成本[6]为目标函数,具体如下:

f=CF+CM+CE+CB-CS

(1)

式中:CF为燃料成本;CM为分布式电源的设备维护成本;CE为污染物排放引起的环境惩罚成本;CB为购电成本;CS为售电收益。计算式如式(2)、式(6)～式(9)所示。

(2)

式中:T为调度周期;t为调度周期内的一个时段;CFC(t)为t时段内燃料电池的燃料成本;CDE(t)为t时段内柴油机的燃料成本;CMT(t)为t时段内微型燃气轮机的燃料成本。

CFC(t)、CDE(t)和CMT(t)的计算公式如式(3)～式(5)所示。

(3)

(4)

(5)

式中:Qm为燃料电池所用燃料的价格;LFC为燃料电池所用燃料的低位热值;PFC(t)为燃料电池的输出功率;ηFC为燃料电池的电能转换效率;a、b、c为柴油机的燃料成本系数;PDE(t)为柴油机的输出功率;Qg为天然气价格;PMT(t)为微型燃气轮机的输出功率;ηMT为微型燃气轮机的电能转换效率;LMT为天然气的低位热值。

(6)

式中:N为微电网系统内分布式能源的种类数;Kn为第n种分布式电源单位输出功率的维护成本系数;Pn(t)为t时段内第n种分布式电源的输出功率。

(7)

式中:M为产生的污染物种类数;Y为产生污染物的电源数;Hn.y为第n种电源输出单位功率时生成第i类污染物的质量;Dn.y为惩罚成本系数。

(8)

式中:cbuy(t)为购电成本系数;Pbuy(t)为购电功率。

(9)

式中:csell(t)为购电成本系数;Psell(t)为购电功率。

1.2 约束条件

(1) 功率平衡约束:

(10)

式中:Pload(t)为微电网系统负荷。

(2) 分布式电源出力约束:

Pn.min≤Pn(t)≤Pn.max

(11)

式中:Pn.min为第n种分布式电源的最小输出功率;Pn.max为第n种分布式电源的最大输出功率。

(3) 可控分布式电源爬坡约束:

(12)

式中:PFC(t+Δt)、PMT(t+Δt)和PDE(t+Δt)分别为第t+Δt时段燃料电池、微型燃气轮机和柴油机的输出功率;PFC(t)、PMT(t)和PDE(t)分别为第t时段燃料电池、微型燃气轮机和柴油机的输出功率;PFC.down、PMT.down和PDE.down分别为燃料电池、微型燃气轮机和柴油机的最小爬坡率;PFC.down、PMT.down和PDE.down分别为燃料电池、微型燃气轮机和柴油机的最小爬坡率。

(4) 蓄电池储能约束:

ESOC.min≤ESOC(t)≤ESOC.max

(13)

式中:ESOC(t)为蓄电池t时刻的荷电状态;ESOC.min、ESOC.max为蓄电池荷电状态的最小值和最大值。

(5) 购、售电功率约束:

(14)

式中:Pbuy.max、Psell.max分别为购电功率最大值和售电功率最大值。

2 改进帝国竞争算法

2.1 帝国竞争算法

帝国竞争算法(imperialist compertitive algorithm,ICA)是基于帝国主义国家之间的竞争提出的一种优化算法。种群中包含两部分:一部分是帝国,另一部分是殖民地。每个帝国势力由代价函数决定,强势帝国通过兼并占用其他弱国殖民地实现帝国竞争,从而使种群收敛至全局最优解。ICA算法的优化原理可参考文献[7]。

2.2 高斯-柯西变异帝国竞争算法

1)高斯变异[8]

ICA算法中殖民地被占领时收敛速度慢,为了解决这一问题,对殖民地进行高斯变异,使算法在重点区域进行局部搜索,从而提升算法的局部寻优能力。

高斯概率分布函数如下:

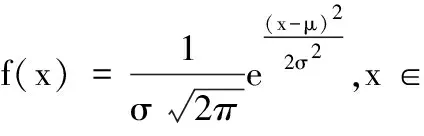
(15)

将殖民地执行式(16)中的高斯变异,其表达式为:

(16)

2)柯西变异[9]

在帝国竞争过程中,当帝国数量减少到初始状态的一半时,帝国在附近区域交换殖民地,ICA算法容易陷入局部极值。为了避免算法陷入局部最优,当帝国数量减少到初始状态的一半时,将剩余帝国以一定概率执行柯西变异。柯西密度函数步长更长,其变异产生的后代与父本差异性较大,变异范围更广,能够使算法跳出局部最优。

柯西概率密度函数如下:

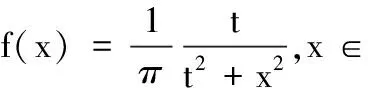
(17)

将剩余帝国执行式(18)中的高斯变异,其表达式为:

(18)

3 GCICA求解微电网优化调度模型

本文采用高斯-柯西变异帝国竞争算法对微电网优化调度模型进行求解,主要求解步骤如下。

(1) 设置调度周期及微电网运行参数。

(2) 将式(1)作为适应度值,并对初始适应度值进行计算。

(3) 随机生成初始国家种群,形成帝国和殖民地,并设置GCICA算法的相关参数,主要种群规模、帝国数量、殖民地影响率和改革率等。

(4) 殖民地向帝国移动,如果殖民地代价小于帝国,则交换殖民地与帝国的位置。

(5) 挑选出最弱殖民地,对其进行高斯变异,计算最弱殖民地被帝国占领后的代价。

(6) 如果某帝国殖民地全部被占领,则该帝国灭亡,当帝国减少至初始帝国数量的一半时,则对殖民地进行柯西变异。

(7) 判断是否满足迭代终止条件,若是则输出最优解,否则返回步骤4。

4 仿真分析

采用图1中的微电网系统进行算法分析,该系统中分布式电源有风电、光伏、微型燃气轮机、柴油机和燃料电池,配置有蓄电池储能装置,并与配电网连接。其中:风电机额定功率为250 kW,维护系数为0.031 元/kW;光伏电池额定功率为150 kW,维护系数为0.019 元/kW;微型燃气轮机额定功率为120 kW,维护系数为0.012 元/kW,运行效率为40%,燃料成本为5.14 元/kg,低位热值为51.26 kJ/g,爬坡速率最大值和最小值分别为15 kW/min和-15 kW/min;柴油机额定功率为150 kW,维护系数为0.007 元/kW,运行效率为36%,燃料成本为7.05 元/kg,低位热值为42.55 kJ/g,爬坡速率最大值和最小值分别为12 kW/min和-12 kW/min,柴油机的燃料成本系数a、b、c分别为0.000 85、0.12和6;燃料电池额定功率为120 kW,维护系数为0.017 元/kW,运行效率为51%,燃料成本为2.43 元/kg,低位热值为22.69 kJ/g,爬坡速率最大值和最小值分别为10 kW/min和-10 kW/min;蓄电池荷电状态初始值为0.4,其最大值和最小值分别为0.8和0.2。

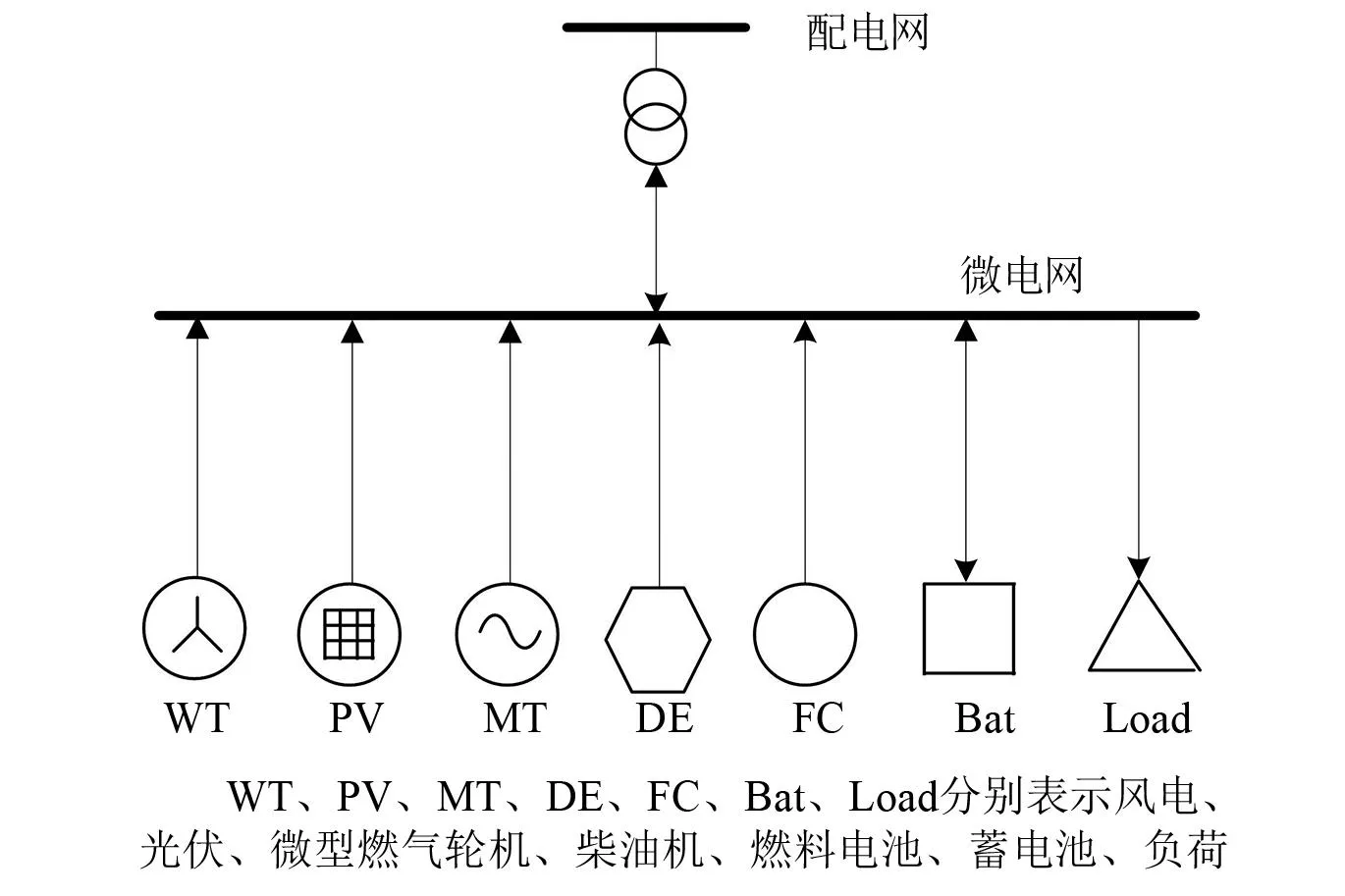
图1 微电网结构图

微型燃气轮机、燃料电池和柴油机在运行过程中会产生大气污染物,相关排放系数参考文献[10]。微电网与上级电网电能交换采用分时电价,具体参考文献[11]。设置调度周期为24 h,将一个周期划分为24个时段进行优化调度,调度日当天风电、光伏出力及负荷变化如图2所示。由于风电和光伏在发电过程中清洁无污染,且不消耗化石能源,因此微电网优化调度优先考虑风力发电和光伏发电。

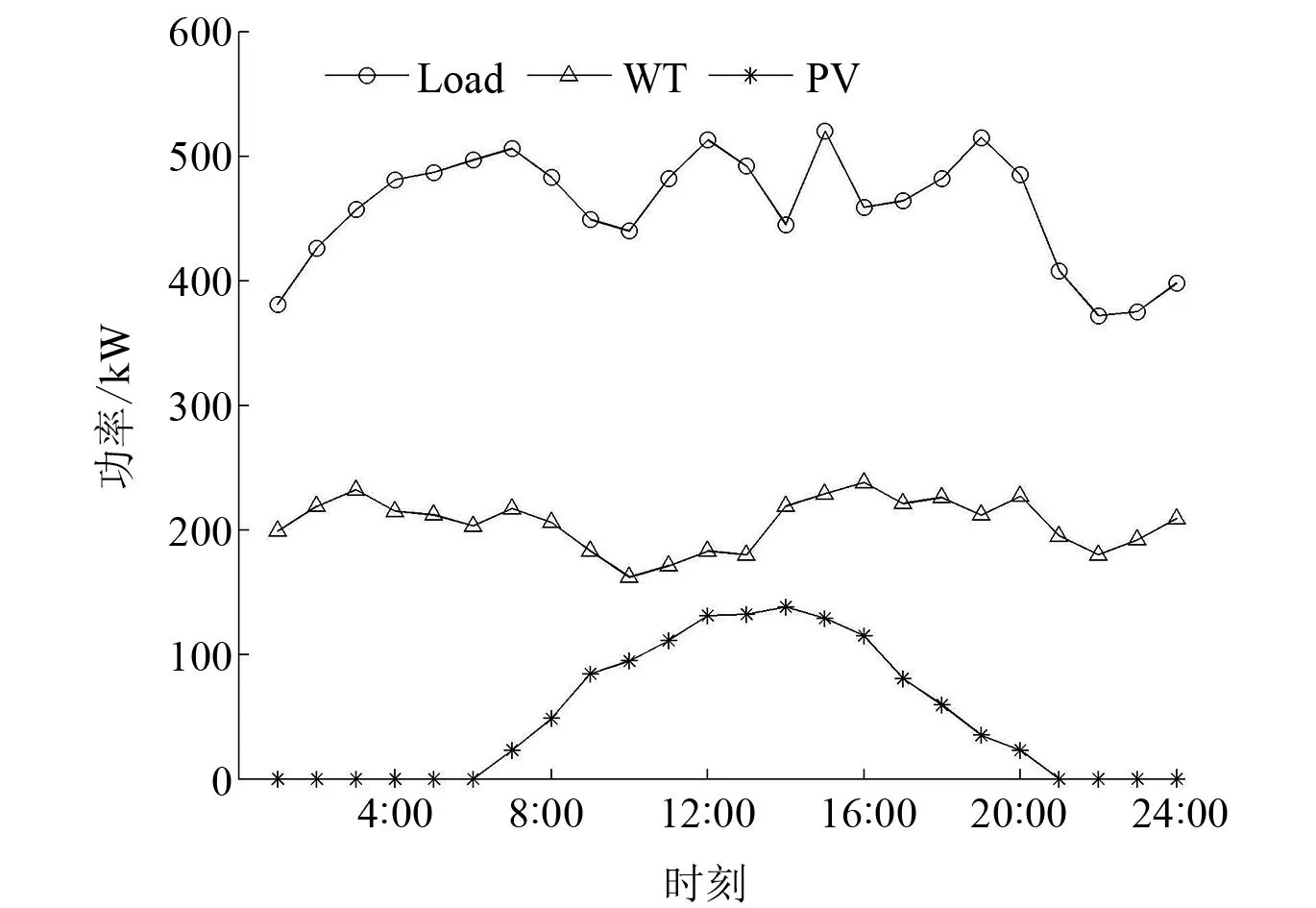
图2 调度日当天风电、光伏出力及负荷变化

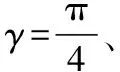
图3 四种优化算法稳定性对比

表1给出了四种优化算法的最优解、收敛次数和迭代时间。由表1可知,GCICA算法只需52次迭代即可找到最优解,最优解为4 485.62元,对应的收敛时间为2.54 s,在最优解、收敛次数和迭代时间方面全部优于其他算法。相比ICA算法,微电网综合运行成本下降88.61元,收敛次数减少71次,收敛时间缩短1.11 s。由此可见,采用高斯-柯西变异的帝国竞争算法能够有效减少迭代次数,加快算法收敛,提高计算精度。GCICA算法取得最优解时,微电网系统在调度日当天的各项运行成本如表2所示。

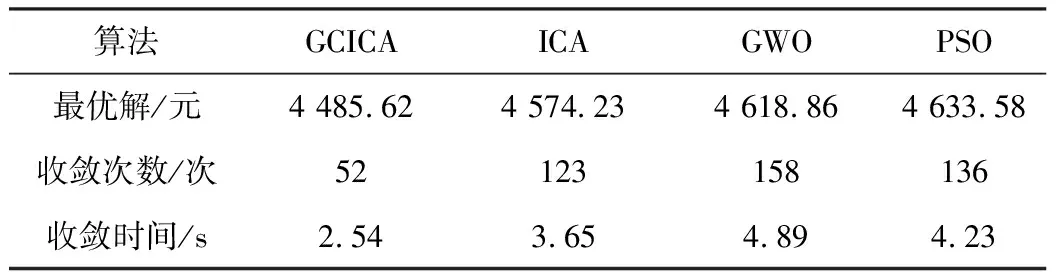
表1 四种算法优化结果对比

表2 调度日当天各运行成本 单位:元

图4～图6给出了调度日当天微电网系统内各分布式电源的出力情况及微电网与上级配电网之间的购、售电情况。

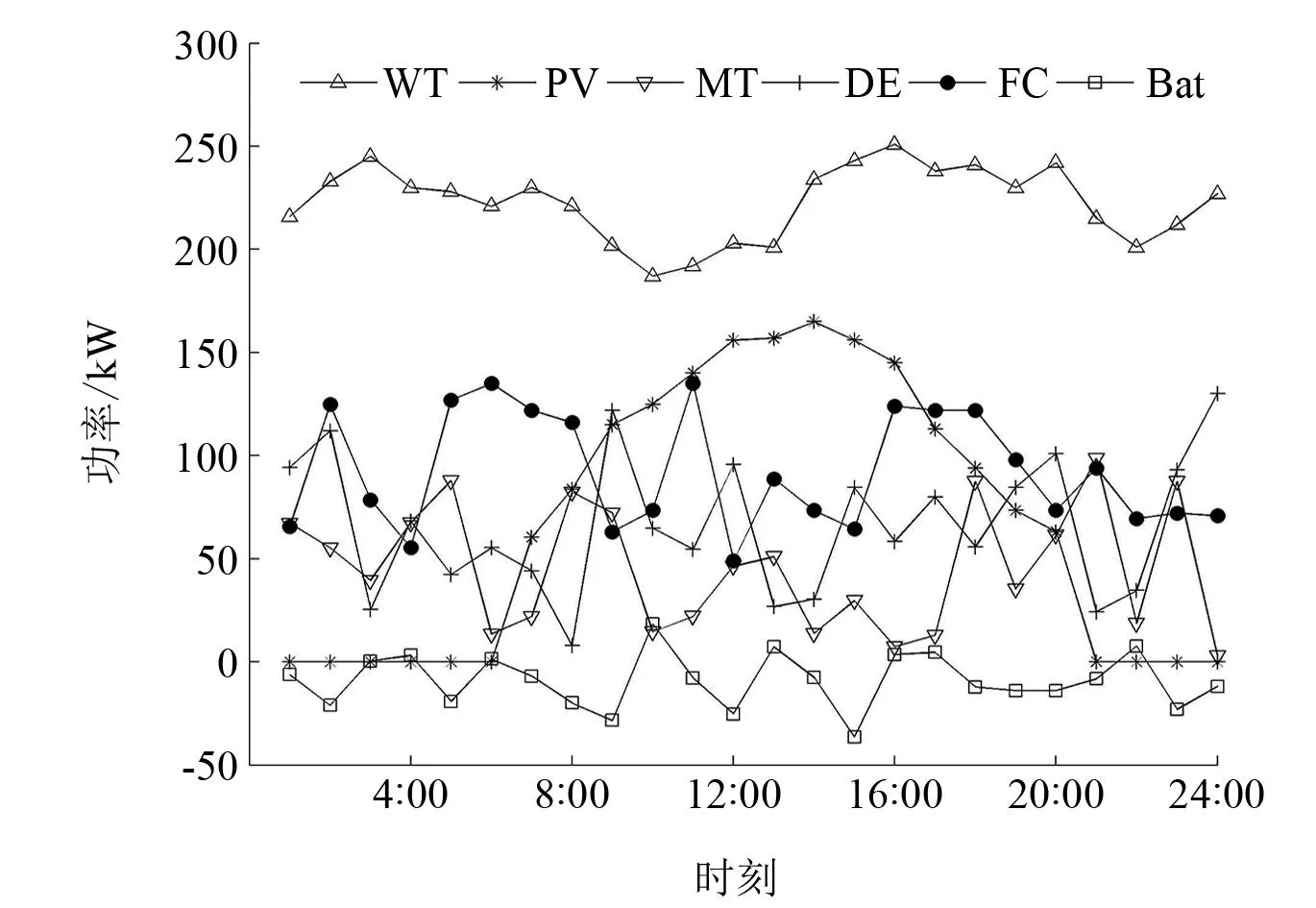
图4 调度日当天微电网系统内各分布式电源的出力曲线

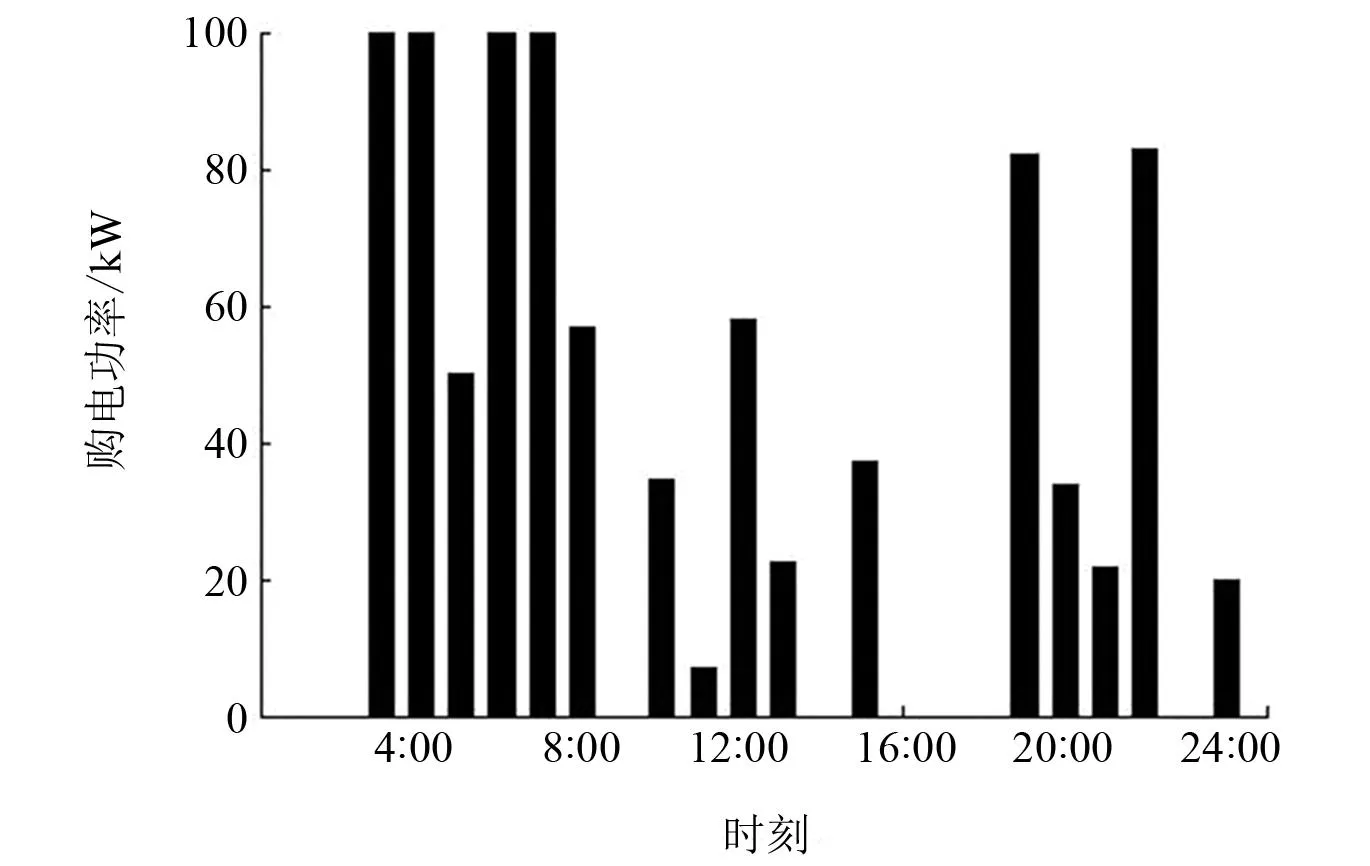
图5 调度日当天微电网购电功率

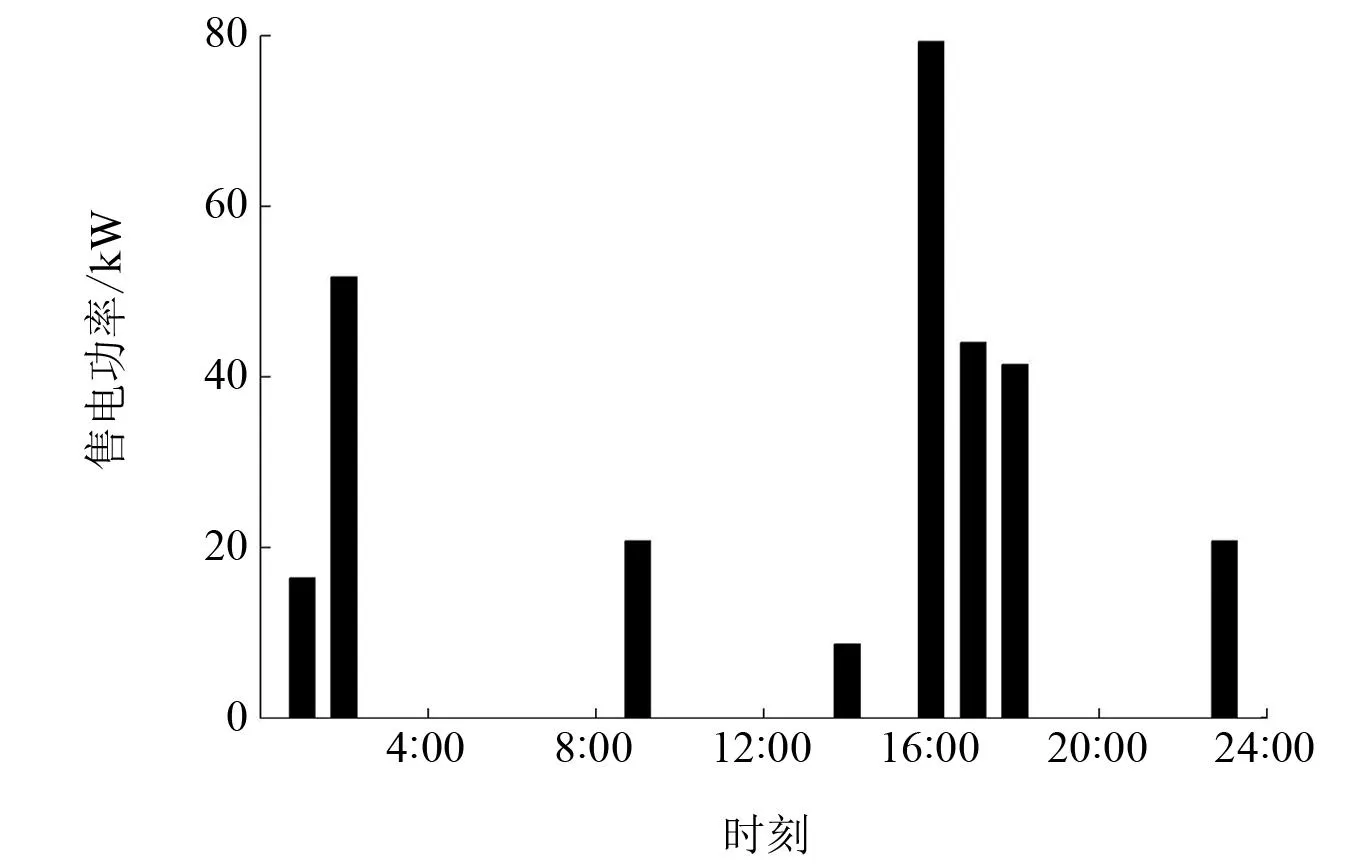
图6 调度日当天微电网售电功率

结合图4～图6可知:在用电低谷时段,以0∶00—2∶00为例,微电网系统负荷较小,在满足风电消纳的基础上,微型燃气轮机、柴油机和燃料电池等耗能分布式电源出力较小,在满足系统负荷需求的前提下优先考虑给蓄电池充电,并将多余电能向配电网出售获取部分收益;在用电平时阶段,以13∶00—14∶00为例,系统负荷需求相对较大,风光资源相对充足,在保证风光消纳的基础上,负荷缺口由耗能分布式电源和蓄电池提供;在用电高峰时段,以18∶00—21∶00为例,系统负荷需求相对较大,风光资源相对匮乏,负荷缺口较大,此时耗能分布式电源出力较大,并向上级配电网购买一定电能以满足负荷需求。综上所述,在调度周期内, 综合考虑燃料成本、设备维护成本和环境惩罚成本,优化微电网系统内各分布式电源出力,系统发电量不足时向上级配电网购电,系统发电量充足时向上级配电网售电获取收益,从而使微电网综合运行成本最小。

5 结束语

本文建立了以综合运行成本最小为目标函数的微电网优化调度模型,采用高斯-柯西变异帝国竞争算法对模型进行了求解,获得微电网最佳调度方案。在此方案下,微电网最小综合运行成本为4 485.62元,各分布式电源出力合理,优先使用风光电能,降低污染物排放量,并能合理与上级配电网交换电能,可见该模型在微电网优化调度领域具有较大的工程应用价值和推广前景。