基于机器学习的TBM破岩效率预测模型研究

刘俊峰 陈杜楷 区志钊 邹相荣 凌钧昊 叶梓健

(东莞理工学院 生态环境与建筑工程学院广东省城市生命线工程智慧防灾与应急技术重点实验室,广东东莞 523808)

面隧道掘进机(Tunnel Boring Machine,TBM)因为其稳定性佳、运行速度快、操作简便等优点被广泛应用于隧道施工中。相对一般的钻爆技术来说,TBM拥有操作迅速,破岩快速的优越性,所以在TBM施工过程中的破岩效率问题成了需要关注的主要问题之一。对该问题的研究,学者们主要利用理论分析、现场测试与数值模拟等方法展开了大量滚刀破岩效率分析。乔世范[1]基于比能耗理论构建了TBM比能耗预估模型,温森[2]等人对软硬相间岩层中滚刀旋转切割的破岩效率开展动态分析,发现随着刀盘贯入度的增加,滚刀法向力与滚动力均有所增加。BRULAND[3]建立了NTNU模型,以节理倾角为变量研究了TBM的破岩效率;温森等[4]运用PFC3D与UDEC离散元模拟软件对复合地层滚刀破岩效率、围压、节理等各种因素展开了深入研究。刘立鹏[5]等人运用PFC2D系统开展了TBM双滚刀破岩模式的数值模拟。但因TBM施工环境千差万别,对滚刀破岩效率的影响因素也错综复杂,而当前的理论研究、与数值模拟都无法完全真实地模拟客观的地质现状[6-10]。此外,当前人工智能算法在TBM领域应用主要集中在TBM滚刀磨损预测等方面,对破岩效率智能评估方面的研究和应用并不多[11-14]。基于此,本文依托重庆轨道交通十号线二期工程,运用遗传算法(GA)优化的BP神经网络,以项目所在地采集的花岗岩为研究对象进行室内试验,将试验产生的岩渣形态参数指标作为模型输入参数,以比能为模型的输出参数,建立TBM破岩效率预测模型,预期的结果可为复杂的地质条件下TBM盾构施工优化设计提供一定的理论指导。

1 试验介绍

1.1 试件制备

以天然花岗岩(见图1a)为试件材料,加工成200 mm×140 mm×30 mm的长方体,见图1b。Johnson[22]认为,试验中为减小试件尺寸效应的影响,滚刀下方岩石试件塑性区深度和试件宽度比值应小于1/6。同时,Alehoseein等学者[23]的分析表明岩石试验中花岗岩内塑性区的深度是2 mm,因此可以认为本试验中试件尺寸选取较合理。

图1 花岗岩试件照片

1.2 试验设备

本文中二维滚刀破岩试验在岩石剪切流变仪上开展,试验设备由加载装置与信息采集装置构成,如图2。信息收集装置包括刀具位移传感器与滚刀侵入轴向荷载传感器。在水平方向上对试件施加荷载以模拟地层内的围压,通过滚刀对岩体施加竖向荷载,模拟TBM刀盘力。在加载过程中,对岩石剪切流变仪中横向围压、竖向位移与轴向荷载信息通过计算机进行实时控制与记录。

图2 二维滚刀破岩试验系统

试验中加载系统由岩石剪切流变仪提供,使用的剪切流变仪型号为600WDAJ-600。试验机在试验中通过油缸压力为岩体试件施加横向围压,起到固定的作用,同时施加轴向荷载,模拟滚刀刀盘推力,通过计算机调节滚刀贯入度进控制制滚刀推力。实验中流变仪油缸轴向和横向最大加载力可达到600 kN,变形速率调节范围为0.001～10 mm/min,最大位移可达30 mm。

实验中滚刀为自制的“V”形盘形滚刀,采用H13型高硬度模型钢制成,洛氏硬度达到了45～55 HRC,实际强度与工程中TBM盘形滚刀强度基本一致。滚刀边缘宽13 mm,滚刀圆心角为18°,刀刃角为19°,试验设备下侧设置方形底座,与上部滚刀相连接,以增强试验设备稳定性。

2 TBM破岩效率预测模型

2.1 BP神经网络(BPNN)

BP神经网络(Back Propagation Neural Network,BPNN)利用误差反向传达,持续改正每个神经元间的连接权值与阈值,进而获得训练效应,主要的结构模型如图3[15-17],BPNN的主要结构涵盖了输入层、输出层与隐藏层。输入层是输入信号的树突,输出层生成编辑过的数据的终端,隐藏层便是神经网络数据编辑层。

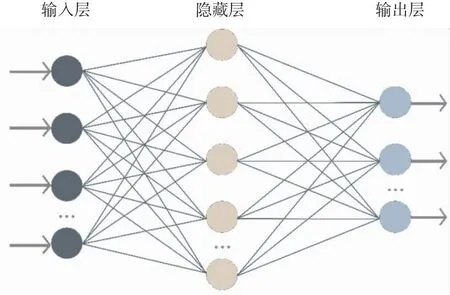
图3 BP 神经网络结构图

BP神经网络必须利用信号正向传递与误差反向传达两种操作,信号正向传达时,从输入层进入,经历隐含层的神经元节点激活,进入输出层后将输出值和期望值对比,若存在误差则实施误差反向传递的操作。此阶段通过改变每个层的权值与阈值,将误差平均到每层神经元中,以达到误差梯度下滑的效果,最终在误差满足精度标准时,学习终止,输出预测值[18-20]。

2.2 输入参数选取及数据预处理

模型采用三层神经网络结构,模型输入层和输出层节点数分别为6和1,包含6个输入参数和1个输出参数。隐藏层神经元数量的确定则参照经验式(1)确定。

K=a+b+c,

(1)

其中,a、b是输入层和输出层节点数,c取1～10之间的常数,K为隐藏神经元数量。K的取值范围是8～17,传递函数选用sigmoid函数。

①输入参数选取。

输入参数包括3种类型。第1种为节理岩体参数,由于使用的试验材料属于天然花岗岩条石材料,完整岩体单轴抗压性、抗拉能力通常由其弹性模量与黏聚力的宏观力学表现,而对于含有节理的岩石材料,其力学特性往往取决于节理条件,因此本文选取节理倾角α与节理间距D为输入参数来研究节理岩体的TBM破岩效率。

第2种为TBM机械参数,由器械在TBM中的参数传感器得到,如刀盘推力(Fn)、贯入度(p)、扭矩(T)、转速(RPM)等,而在本试验中,滚刀贯入度为10 mm不变,因此选取了法向推力Fn和刀间距S两个输入参数。

因本研究需基于基岩渣的几何特征来分析滚刀破岩效率的影响要素,所以第3种参数设定为岩渣特点参数指标,采用岩渣几何特点(短轴c、中轴除以长轴的结果b/a)作为输入参数,将比能作为模型的输出参数,构建TBM破岩效率预估模型。

②数据预处理。

对数据实施归一化处理是建模与训练前的重要工作,由于各种输入参数的量纲与量纲单位通常存在一定的差异,因此在每个输入参数的量级有显著的不同时,直接以初始的输入参数来建模,会使数值较高的参数在分析中的影响程度大于数值低的参数。此外,将获得的数据归一化处理还可以增强预测模型的计算速度、精度和计算结果的准确度。本文通过式(1)将样本的每个参数转化成无量纲的数值,最终映射到0和1之间。

(1)

2.3 基于粒子群算法优化的支持向量回归(PSO-SVR)预测模型建立

对于支持向量回归算法来说,不敏感损失系数ε、惩罚因子C和核函数参数σ等参数的优化选择对SVR模型的学习精度和泛化能力的优劣起决定性作用[23]。

不敏感损失系数ε关系着回归函数对不敏感区域的宽度。ε取值的既要满足最大间隔原则,又要提高模型的学习精度。位于条带区域内为样本点集中分布区域,位于外部为样本点分散分布区域,而条带宽度范围应尽量包含所有样本点,却不能同时过大。若ε超出了一定的范围,支持向量数偏少,学习精度较差;若ε过小,学习精度强,支持向量的数量高,可能使模型计算过于复杂。因此,可以发现此时不敏感损失系数ε对支持向量的数量具决定性影响,且对学习精度与泛化能力的同样意义重大。

惩罚因子C是对位于ε范围以外的信息点给出的惩罚方案。该值越大,惩罚越严苛,学习精度越高,同时也会使模型拟合过度,导致泛化水平下降。基于结构风险最小化理论,如果说不敏感损失系数控制经验风险的大小,那么惩罚因子C则影响着置信风险的范围,应调节模型参数使经验风险和置信风险之和最小。

针对非线性问题,通过引入核函数实现从非线性学习到线性学习的转化,把高维空间映射到更高维的空间,加强线性可分性(表1)。本文引入RBF高斯径向基核函数,其具有比其他核函数更好的总体性能,如局部性强、学习能力较强等。

表1 SVR 常用核函数

综上,SVR参数(C、σ、ε)的优化抉择对扶持向量回归性能的影响较大,引入PSO优化算法实现对参数的优选,步骤如下:

Step 1:将SVR参数C、σ、ε视为粒子给予初始化,将种群数量界定为20,迭代次数的上限值是200,学习因子c1与c2取为1.5。记录个体极值pbest和全局极值gbest。

Step 2:算出现阶段群体中每个粒子的适应度值。设置所有粒子的适应度值,为其现阶段的个体极值值pbest,每个粒子中适应度最佳的设置为全体极值。

Step 3:将粒子的速度与地点进行更新,同时对比前一时刻的极值,对个体极值与全局极值给予更新。

Step 4:判断程序迭代计算次数是否达到最大,或者满足最小误差条件。若结束条件满足,则迭代运算停止,输出参数最优解。

3 基于机器学习的TBM破岩效率预测模型验证与结果评价

经过参数调整测试,将PSO参数学习因子c1与c2设定为1.5、种群规模为20、最大迭代次数200,SVR的核函数是高斯核函数RBF,通过粒子群优化SVR的关键参数,图4为得到的模型适应度变化,其中模型最优适应度为0.018 01,表明在该参数取值条件下模型迭代计算具有较好的收敛性能。

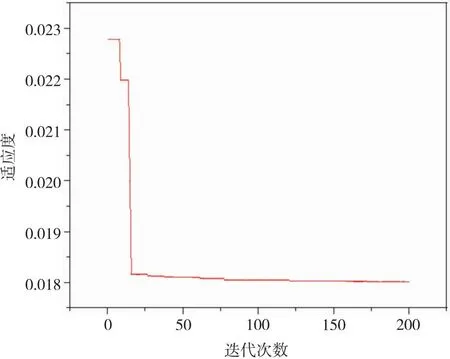
图4 PSO-SVR模型适应度曲线

将100组试验数据分成两部分,分别为训练集(80%)和测试集(20%)。前文建立的PSO-SVR预测模型经过80组训练集数据的学习,得到的TBM破岩比能实测值和预测值变化趋势对比图如图5所示。再对20组测试集数据进行预测,得到的破岩比能预测值和实测值对比图如图6。由图5和图6训练集和测试集的预测对比可以看出,比能预测值曲线贴近实测值曲线,预测结果较为准确。

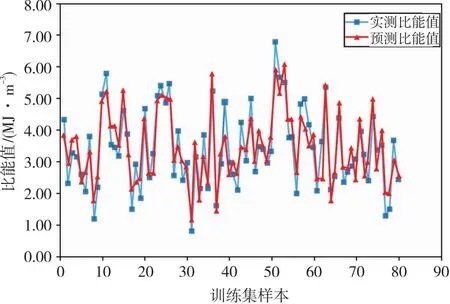
图5 PSO-SVR模型训练集比能实测值和预测值对比图

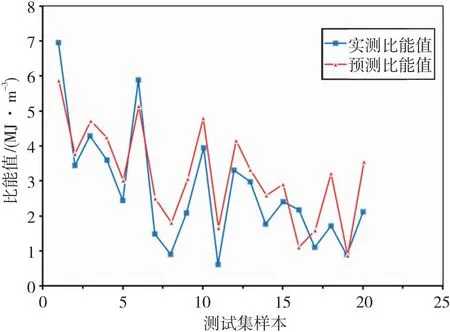
图6 PSO-SVR模型测试集比能实测值和预测值对比图

PSO-SVR预测模型测试集的均方差MSE是0.629,均方根差RMSE是0.793,同时给出测试集信息的相对误差如图7。由图7结果可以发现,20个样本的相对误差上限值是89.21%,相对误差下限值是3.27%,平均相对误差是30.44%,有45%的样本相对误差超过平均相对误差。在比能值低于2.5 MJ/m2的情况下,相对误差相对显著。将4组比能值低于2.5 MJ/m2的测试集数据剔除后,样本的相对误差上限值是40%,相对误差下限值是3.27%,平均相对误差是17.7%(图8),这意味着此模型在比能较小状况下的预估精度还有待提高。PSO-SVR预测模型的预测值相对于误差极差较小,离散性同样也较小,预测能力相对稳定,而通过平均相对误差也可以看出整体预测精度也较高。

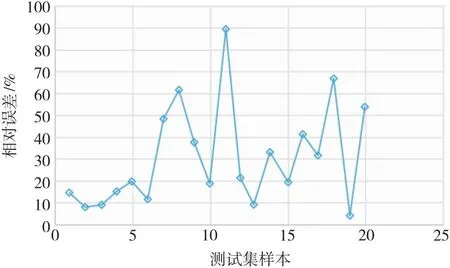
图7 20组测试集数据PSO-SVR模型测试集相对误差图

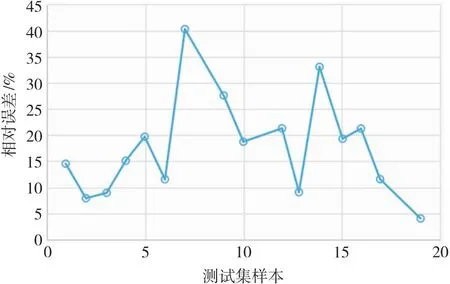
图8 比能值高于2.5 MJ/m2测试集数据PSO-SVR模型测试集相对误差图

最后,绘制100组训练集与测试集信息的线性回归拟合直线如图9所示。拟合曲线的决定系数R2是0.809,而测试集的拟合决定系数R2是0.812,这表明预测值与实测值的相关性相对较高,本文的PSO-SVR模型具有较高的预测精度。

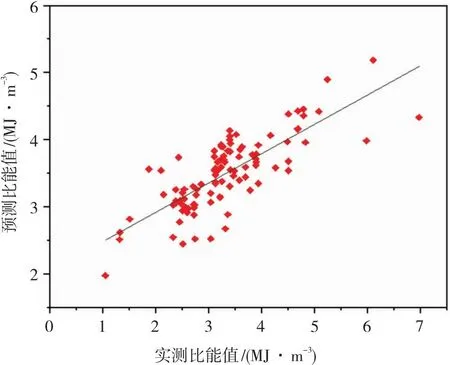
图9 PSO-SVR模型比能实测值和预测值线性回归图

4 结语

以机器学习为理论基础,以节理岩体参数节理倾角α、节理间距D、刀间距S、法向推力Fn、典型岩渣短轴c、中轴与长轴的比值b/a作为模型输入参数,比能SE作为输出参数,基于破岩比能建立PSO-SVR滚刀破岩效率预测模型。结果表明,PSO-SVR模型有较高的相关度,预测结果准确度较高,可适用于TBM破岩效率预测,同时也说明模型所选择的输入参数可以较好地预测TBM滚刀破岩效率,可以为实际隧道工程中TBM施工研究提供一定的理论依据。