带有延迟步长的循环BB梯度法
2024-02-21杨奕涵
杨奕涵
(重庆师范大学 数学科学学院, 重庆 401331)
考虑一般无约束优化问题
(1)
其中目标函数f:Rn→R是连续可微的。求解问题(1)的方法主要有线搜索方法和信赖域方法, 而梯度法是线搜索方法中的一类简单迭代方法, 它以负梯度方向作为搜索方向, 其迭代格式为
xk+1=xk-αkgk,
(2)
其中gk≜g(xk)=∇f(xk),αk为步长。由于搜索方向已定, 梯度法求解无约束优化问题便转化为研究步长αk的选取, 不同的步长选取会导致梯度法具有不同的性能。因此, 如何设计一个有效的步长, 使得问题(1)能被快速求解, 且收敛性具有一定的理论保证, 是研究梯度法的重要问题之一。
最早的梯度法是1847年Cauchy[1]采用精确线搜索步长, 提出了最速下降法(SD法), 其步长为
(3)
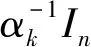
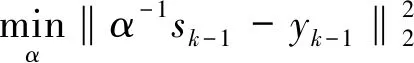
其中sk-1=xk-xk-1,yk-1=gk-gk-1, 得到两个两点步长公式为
两点步长又称为BB步长, 相应的梯度法称为BB梯度法, 简称BB法。对于f为严格凸二次函数的情形, Barzilai和Borwein证明了当n=2时, BB法具有R-超线性收敛速度。自BB法的提出, 极大地改善了梯度法的效率, 其理论上的结果有: 1993年Raydan[3]证明了当f为任意维严格凸二次函数时, BB法是全局收敛的, 并且2002年Dai和Liao[4]进一步证明了BB法具有R-线性收敛速度。此外, 也吸引了众多学者对该方法做一系列研究, 从不同的角度推导了不同类型的BB步长, 如文献[6]-[15]等。
如果直接将BB法推广至求解一般无约束优化问题, 即使目标函数是严格凸函数, 该方法也可能不收敛。因此为保证其收敛性, Raydan[5]在1997年首次将BB步长与GLL非单调线搜索技术[16]相结合, 并证明了该方法是全局收敛的。随后, 求解一般无约束优化问题的BB类方法得到发展, 如文献[17]-[19]等。
本文考虑一般无约束优化问题(1), 基于延迟(retard)策略, 采用前一步迭代的步长为当前迭代步长提供一些重要信息, 推导出一个求解一般无约束优化问题的步长, 进而设计一类高效的BB梯度法。本文的结构安排如下:1)给出了求解一般无约束优化问题的新梯度法, 并进行了讨论;2)给出了本文提出的算法框架;3)给出了该算法的全局收敛性和线性收敛率;4)数值试验验证了与现有技术相比, 所提出的梯度算法在计算上更高效。
1 新步长的推导
对于严格凸二次极小化问题:
(4)
其中A∈Rn×n对称正定,b∈Rn。 2022年Huang等人[15]提出了步长:
(5)
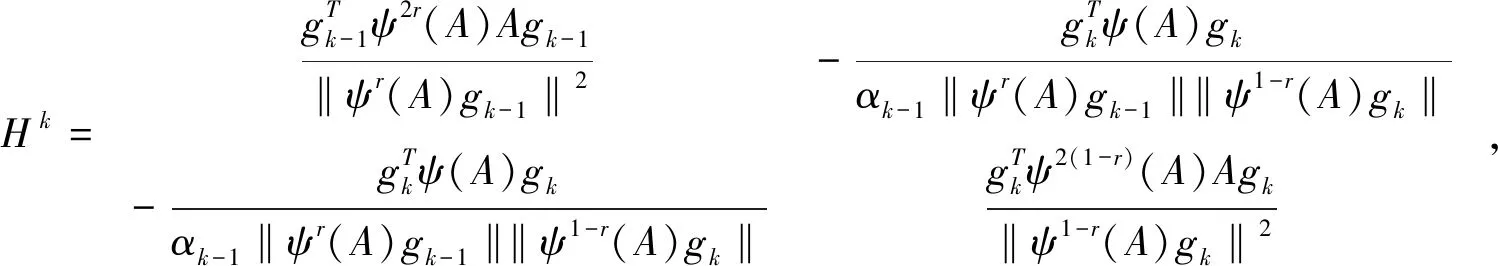
A,可得一个求解二次问题的步长:
αk=
(6)
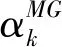
2022年, Zhang和Sun[19]将二次极小化问题推广到求解一般光滑无约束优化问题, 考虑构造前一步BB步长来近似当前Cauchy步长, 其迭代格式为
(7)
(8)
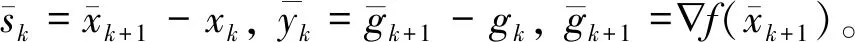
(9)

(10)
由于近年来出现了循环步长更新策略, 如SDC方法[21], 它需要h(≥2)步Cauchy步长(3), 及通过(9)式计算m个固定步长, 其更新策略为
(11)
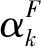
(12)
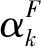
进而Zhang和Sun在文献[19]中提出了一种新的循环梯度法, 其步长为:
(13)
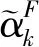
(14)

(15)

考虑二次函数的极小化问题[23]:
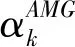
(16)
下一节, 我们将给出步长(16)与Zhang-Hager非单调线搜索技术[24]相结合而设计的循环BB梯度算法(CBBGM算法)。
2 CBBGM算法
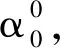
第一步若‖gk‖∞≤ε, 停止。

第三步(Zhang-Hager非单调线搜索)若
f(xk-αgk)≤Ck-δα‖gk‖2,
成立, 执行第四步; 否则, 通过下式更新α, 并执行第三步。
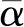
第四步Qk+1=ηkQk+1,Ck+1=(ηkQkCk+fk+1)/Qk+1,ηk∈[ηmin,ηmax].
第五步αk=α,xk+1=xk-αkgk,k∶=k+1, 执行第一步。
3 收敛性分析
本节将证明提出的CBBGM算法是全局收敛的, 并且具有线性收敛速度。下面先对目标函数做如下假设。
假设A 1)f(x)在Rn中连续可微;
2)f(x)在Rn上有下界;
3) 梯度g(x)在Rn上Lipschitz连续, 即∃L>0, 使得
‖g(x)-g(y)‖≤L‖x-y‖, ∀x,y∈Rn。
由文献[24]中的引理1.1可以直接得到下面的引理1。
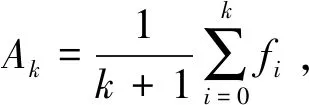
fk≤Ck≤Ak.
为分析CBBGM算法的全局收敛性和线性收敛率, 现需证明下面定理1。
定理1若假设A成立, {αk}是CBBGM算法产生的步长序列, 则∃ξ>0, 使得
αk≥ξ,
(19)


f(xk-ραkgk)>Ck-δραk‖gk‖2≥fk-δραk‖gk‖2.
(20)
因为∇f(xk)是 Lipschitz连续的, 所以
f(xk-αkgk)-f(xk)=
(21)
参照文献[24]中的定理2.2和定理3.1的证明方法, 可以得到CBBGM算法的全局收敛性和线性收敛结果。
定理2若假设A成立, 设{xk}是由CBBGM算法产生的迭代点列, 则有
(22)
此外, 若ηmax<1, 则有
(23)
定理3若假设A成立, 且f:Rn→R为强凸函数,x*是一般无约束优化问题的唯一极小点,ηmax<1, {xk}是由CBBGM算法产生的迭代点列, 则∃θ∈(0, 1), 使得
(24)
4 数值试验
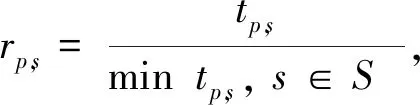
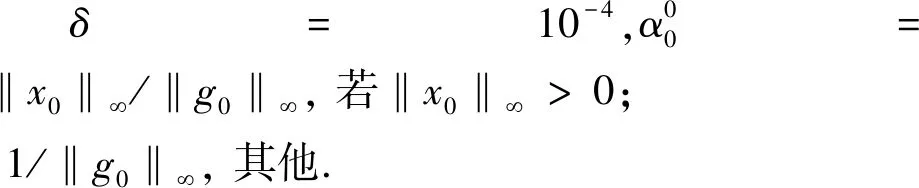
为了更直观的比较四种方法的数值效果, 本文绘制了迭代次数、函数值计算次数、梯度值计算次数和CPU计算时间的性能曲线图, 如图1~图4。从图中可以看出, 在迭代次数、函数值计算次数、计算时间上, 本文提出的CBBGM方法与其他方法相比, 都具有竞争力。在梯度值计算次数上, 由于CBBGM方法是基于上一步的步长信息, 于是在计算下一个步长时, 会计算两次梯度值, 但是CBBGM方法与其他三种方法也是可比的。
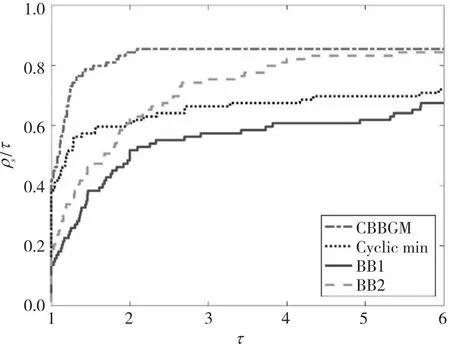
图1 迭代次数性能曲线

图2 函数值计算次数性能曲线
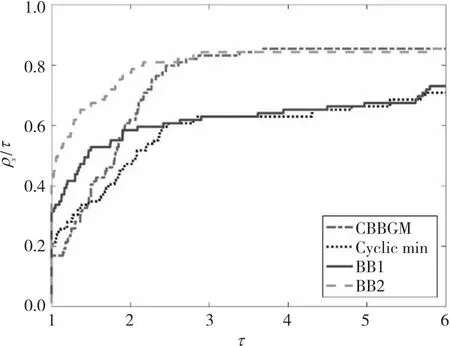
图3 梯度值计算次数性能曲线
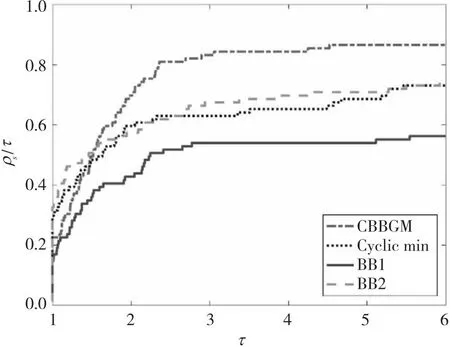
图4 计算时间性能曲线
5 结语

