基于改进灰狼算法的港作拖轮调度研究

姚鹏 段兴锋

(集美大学 航海学院,福建厦门 361021)

在我国维持港口开放与经济发展的背景下,港口规模的扩张与作业需求的持续增长已成为大趋势[1],而今港口船舶众多,港口结构复杂,拖轮资源有限,故拖轮调度问题的优化显得尤为重要。而合理优化拖轮调度能节省大量港口拖轮资源,加快港口船舶运行效率[2]。

拖轮调度问题起源于作业车间调度问题(Job-shop scheduling problem,JSP),传统的拖轮调度主要依靠调度工作人员的经验,辅以一些整数规划方法[3-6],随着港口作业需求量的增大,传统的方法已难以应对新的挑战,就需要有更科学更有效的方法来解决拖轮调度问题。目前相关的研究主要聚焦在建立贴合实际的拖轮调度模型,并采用合适的元启发式算法求解等方面。现有文献大部分拖船调度模式均以拖船最大运行时间为优化目标[7],这与实际应用需求有差距。李伯棠等[8]构建了以拖轮燃油成本最小化为目标函数、考虑多停泊基地条件下的一体化拖轮调度模糊规划模型,设计了鲸鱼—遗传混合算法(Whale Optimization-Genetic hybrid Algorithms based on Scheduling Plan coding,SPWOGA)进行求解,并与CPLEX、Memtic算法进行对比试验,验证了该算法的可行性。Wang等[9]以拖轮平均利用率、船舶平均等待时间和最大等待队列长度为多优化目标,根据调度规则构建混合整数规划模型,结合GA、ACO算法提出GA-ACO算法,对该模型进行求解,验证了该算法的有效性;Chang等[10]基于动态分析,以船舶等待时间和拖船溢出马力最小化构建最佳目标函数,建立拖船动态的调度优化模型,并通过引入熵函数和精英保留策略,改进了基本粒子群算法进行优化研究。刘志勇等[11]针对港口运输路径优化问题,构建最低运输成本的调度模型,并采用了改进后的萤火虫算法进行优化求解。

灰狼优化算法(Grey Wolf Optimization,GWO)是澳大利亚格里菲斯大学学者Mirjalili[12]于2014年提出的一种新型群体智能优化算法,此算法的优点为结构简单、设置参数少、收敛速度快以及全局寻优能力强,故在工程制造[13]、图像信息[14]、能源优化[15]等多个领域均得到应用,其中也包括调度领域。王玉芳等[16]针对柔性作业车间调度问题,采用整数编码方式,提出了一种自适应灰狼算法进行求解,通过引入自适应社会等级分布制度策略提高算法的鲁棒性,以及变领域搜索策略用于平衡算法的寻优能力,但未考虑GWO与整数编码存在一定的冲突,影响到算法的性能;顾九春等[17]建立多优化目标下的节能调度模型,在整数编码的条件下采用GWO进行求解,并通过交叉操作策略进行个体优化,它仅在寻优方面进行调整,并未对初始种群进一步优化;胡泽洲等[18]对于GWO易陷入局部最优的缺点,采用精英反向学习与非线性控制因子策略,分别强化算法的初始种群多样性与搜索性能,但此算法在非多峰函数上的应用效果并不显著,且未考虑多优化目标的求解情况。

针对上述拖轮调度现存模型的构建问题及灰狼算法存在的整数编码冲突问题,本文基于多艘不同单位成本拖轮的复杂条件,以拖轮空驶燃油成本与拖轮助航燃油成本为最小化优化目标,建立混合整数规划模型,提出一种结合小生境技术[19-20]与交叉修正更新策略的灰狼算法进行求解,通过多个规模下的算例进行对比试验,以验证本文所提算法的有效性。

1 港作拖轮调度模型构建

1.1 问题假设

1)任务计划安排:在拖轮任务开始之前,获取到港口当天的船舶作业需求及具体的靠离泊量的相关信息,并按时间顺序为每艘船舶划定任务,同时结合港口现有的拖轮数量、功率等信息,对前后时间相近的任务(前一任务结束时间与后一任务开始时间相近)进行合并,共用部分拖轮;

2)拖轮作业:拖轮完成靠离泊任务后,返回某一基地并等待下一任务(不一定是紧接的任务);

3)拖轮基地:初始状态下拖轮随机分布于各拖轮基地中,拖轮驶入、驶出基地花费时间忽略不计;

4)拖轮功率:各拖轮有固定的行驶功率,具备相应空驶速度;

5)通航规则:港口为单向航道,船舶不能并行。

1.2 参数设定

1)集合。

J,J′为任务或作业的集合,j∈J={1,2,3,…,NJ};0表示任务开始时的阶段;I为拖轮集合,i∈I={1,2,3,…,NI};K为基地集合,k∈K={1,2,3,…,NK}。

2)参数。

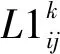
3)决策变量。

1.3 模型建立

以拖轮空驶燃油成本与助航作业燃油成本之和最小化为优化目标,具体目标函数与约束条件如下:

(1)

(2)

(3)

Pi≥Mjxij,∀i∈I,∀j∈J;

(4)

(5)

∀i∈I,j∈{2,3,…,NJ};

(6)

(7)

(8)

(9)

(10)

(11)

模型中,式(1)的3部分分别表示拖船至任务起始点的空载燃料成本、拖船工作时的助航燃料成本、拖船至任务终点的空载燃料成本;式(2)表示每个作业的拖船配置数量;式(3)表示第一次作业之前拖船的位置;式(4)表示完成作业的拖船必须达到目前作业的最小功率需求;式(5)表示第一次作业的拖船应在第一次作业之前就抵达作业起点;式(6)表示拖船在完成上一次作业后,返回停靠基地,并能按时抵达当前作业起点;式(7)表示拖轮必须回到基地,然后再进行下次作业;式(8)表示一个基地目前的拖船数量,应符合完成任务所需要的拖船数量;式(9)表示一艘拖船只能在同一时间内停靠在一个基地;式(10)表示在目前阶段没有任何任务的情况下,拖轮停留在上一基地;式(11)代表变量是0到1的整型变量。

2 面向拖轮调度的HNGWO

2.1 灰狼算法原理

GWO是模仿灰狼群的捕食特点,以狼群追踪、包围、追捕、攻击猎物为目标,实现最优搜索。灰狼的捕猎过程根据式(12)、式(13)实现:

(12)

(13)

其中表示t为当前迭代次数,Xp表示猎物的位置向量,X(t)表示当前灰狼的位置向量;A和C是协同系数向量,根据式(14)、式(15)变化:

(14)

(15)

在狼群的捕食过程中,a由2线性接近至0;r1和r2是[0,1]中的随机向量,显然随着迭代过程的深入,a逐渐减小为0,灰狼逼近猎物,与此同时,r1与r2使得灰狼有机会跳出局部最优解。

2.2 混合小生境技术

由于灰狼算法本身的机制,以及拖轮调度的混合整数规划特性,导致初始种群对GWO在拖轮调度问题上的迭代收敛具有很大程度的影响,所以本文从初始种群入手,引入改进遗传算法中的小生境技术,提高初始种群的多样性,具体如图1所示。

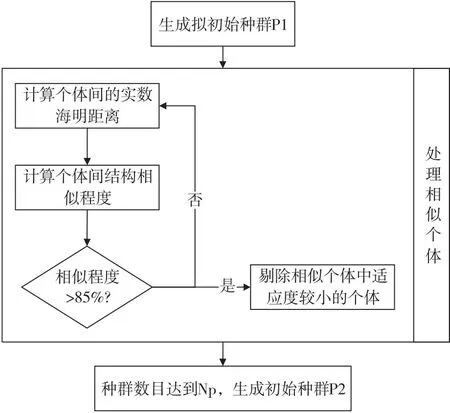
图1 小生境技术路线图

2.3 交叉修正更新策略

灰狼算法的更新过程中往往伴随非整数解的出现,且拖轮调度问题的解个体存在约束限制(主要包括处理同一任务时拖轮不可重复、任务所需拖轮最低功率的限制),灰狼算法更新后的个体极易出现非法解,故本文提出一种交叉修正更新机制,具体步骤如下:

1)根据当前狼的位置与种群中当代头狼α、β、δ的位置,以及当前各自协同系数向量A和C,分别计算当前狼与各头狼的距离向量,取各距离向量的中心;

2)将向量中心修正为整数解(大概率仍然是非法解);

3)根据任务最低功率要求计算可选拖轮集;

4)将2)中得到的非法整数解与3)中的可选拖轮集取交集,进而获取最接近于非法整数解的个体,完成当前个体的更新;

5)对灰狼中包含的所有个体均按上述步骤进行更新,即完成对灰狼个体的更新。

以5个任务、8艘拖轮为例,图2展示了交叉修正更新过程,个体由全部任务所需的拖轮组成,其中当前个体基于参数A、C与当前代3个头狼α、β、δ进行交叉融合,经取整后得到下一代灰狼位置向量X1、X2、X3,取3者向量中心并修正,再与可选拖轮集取交集(个体余下缺失部分随机选取),完成对当前个体的更新,重复多个个体的更新后最终得到新一代灰狼个体。

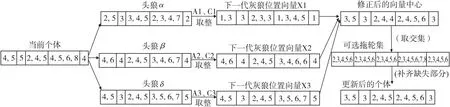
图2 交叉修正更新实例

3 HNGWO算法流程

主要以小生境技术初始化种群,并针对拖轮调度问题的特点,引入交叉修正更新机制,算法流程如图3所示。

图3 算法流程图

4 算例分析

4.1 多规模算法结果对比

为验证HNGWO在港作拖轮调度中的求解效果,本文生成多个不同规模的算例,模拟不同规模的拖轮调度情况,算例规模如表1所示。

表1 算例规模

针对表1所设算例规模下的拖轮调度问题,分别采用CPLEX(数学求解器)、GA、GWO、HNGWO进行求解对比,求解指标采用最优值(Bes.)、平均值(Avg.)、收敛代数(Con.),各代码均使用软件python3.7编写代码(CPLEX为python代码调取函数库使用),运行环境为11th Gen Intel(R)Core(TM) i5-11400H @ 2.70 GHz处理器、16 GB内存、Windows(64位操作系统)的笔记本电脑,具体求解结果如表2所示。

表2 各算法求解结果对比

表2中对比了6个不同规模算例下的算法求解结果,显然HNGWO在各个指标上的表现均优秀,最优值相较于同类智能算法GA、PSO得到了优化,且随算例规模的增大,该调度问题的维度不断提高,各算法的性能差距愈发明显,具体如表3,最优值优化比例也随规模增大不断升高,且HNGWO的收敛速度相较于原始GWO有了显著提升,收敛速度采用指标(Cona.)衡量,Cona.为达到最优解时的当前迭代次数, HNGWO相比于GWO的收敛代数优化比例见表4,可以看出,随算例规模的增大Cona.随之提升,并趋于稳定。本文所给出的6个算例中,Cona.平均值达13.23%,因HNGWO增加了每代种群的多样性,在空间搜索中能更快地定位到最优解附近,但它会导致其最终种群的平均值稍差。

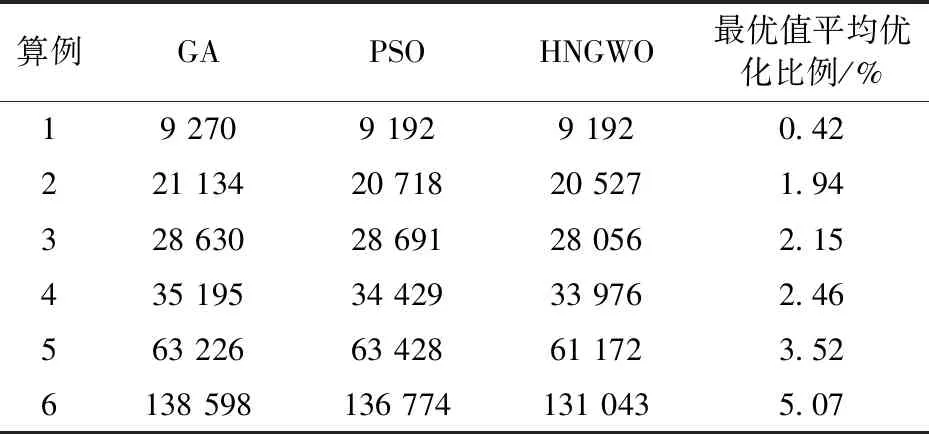
表3 最优值优化对比

表4 收敛代数优化对比

其中CPLEX作为数学求解器,求解精度最高,求解速度极快,但求解至算例5、算例6时却无法获得结果,由此可见CPLEX无法求解大规模调度问题;对于GA算法,针对此类高维度复杂问题时,受限于搜索空间,当搜索空间范围不断增大时,表现较差;而PSO算法,同样受到解个体的维度限制,可以看出PSO算法在小规模算例(低维度)中的表现较好,但当全局学习对象仅有一个时,在大规模算例中易陷入局部最优;而对于原始灰狼算法GWO,相比较于GA、PSO更为优秀,但其收敛速度较慢,这是由GWO求解整数规划问题时的冲突所致。

4.2 中等规模收敛曲线验证

为进一步验证HNGWO的求解效果,选取中等规模的算例3进行不同算法的迭代曲线验证,算例3的拖轮相关数据、任务相关数据如表5、表6所示。

表5 任务相关数据

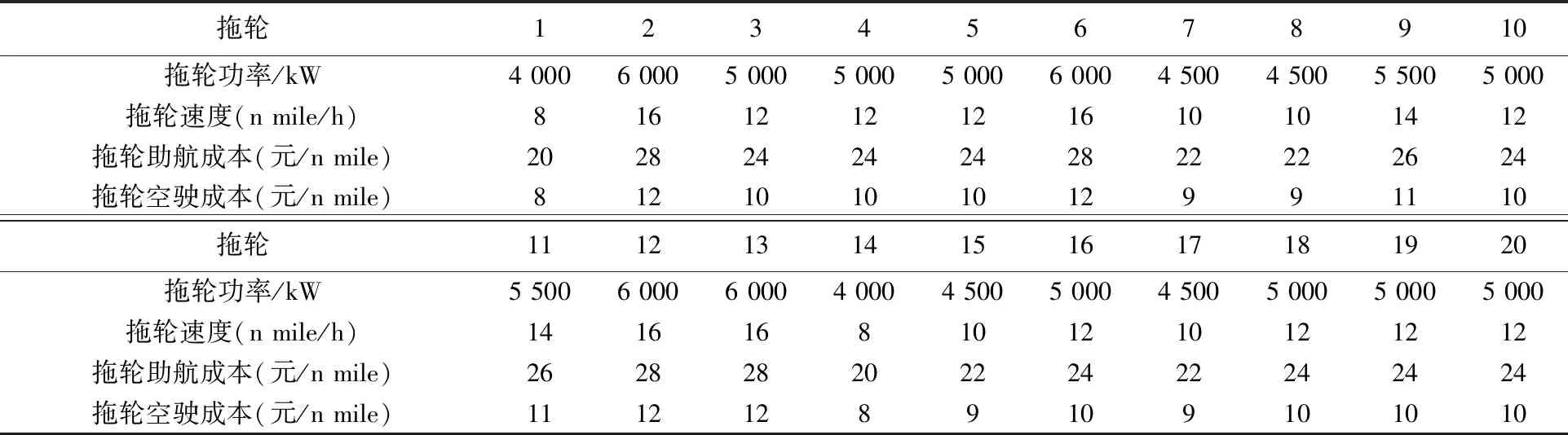
表6 拖轮相关数据

对比同等规模下GA、PSO、GWO、HNGWO的最优解迭代曲线,如图4所示,可以看出:GA由于缺少GWO的交叉修复更新机制,收敛速度会快一些,但最优解较差,PSO面对高维度问题时则早早陷入局部最优,而GWO与HNGWO的求解效果显然更好,两者的最优值相差不多,但HNGWO的收敛速度较快,在港口的实际应用中能有效提高调度效率。

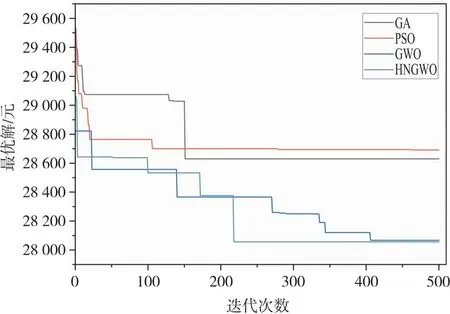
图4 中等规模下各算法迭代效果对比

针对该算例,由HNGWO生成最优调度方案的甘特图,如图5所示,可以清晰地看出,各拖轮执行任务的时间段与作业情况,如4号拖轮执行任务的顺序为任务1—任务9—任务14,执行任务3的拖轮为5号拖轮、9号拖轮、19号拖轮。受拖轮功率的影响以及任务需求的变动,最优调度方案中各拖轮的使用率并不均衡,即在不同条件下得到的动态求解方案可以为港作拖轮调度问题提供参考。

图5 最优调度方案甘特图

5 结语

为求解单向拖轮调度问题提出了一种基于小生境技术的改进灰狼算法,在不同规模的船舶情况下进行对比试验,验证了该算法在拖轮调度领域的可行性。主要贡献有3点:1)设定不同拖轮成本的多目标函数,构建基于混合整数规划的港作拖轮调度模型,并根据船舶作业时间划分多个任务,便于后续求解;2)在灰狼算法的理论基础上,混合小生境技术优化GWO的初始种群,增加了初始种群的多样性,使算法加快收敛;3)在应用GWO求解拖轮调度问题的过程中,存在整数冲突问题(GWO基于非整数解进行收敛,而拖轮调度问题为整数解),采用交叉修正更新策略进行处理,并使算法相较于传统GWO更快收敛至最优解,为港口拖轮调度实践提供解决思路。

本研究存在的不足:首先,算法针对拖轮调度问题作出交叉修正更新环节的改进,导致该混合算法在非整数规划领域的适用性不强,需要进行一定的修改才能应用;其次,算法并未对GWO的后期收敛趋缓问题进行改进,这将是后续改进方向,目前则主要考虑以贪心算法、马尔科夫过程等方法加快GWO的后期收敛性能,得到更优秀的港作拖轮调度方案。